A mathematical model of tuberculosis (TB) transmission with children and adults groups: A fractional model

1.   Introduction

The human population has not been spared by infectious diseases irrespective of the medical facilities. In spite of great achievement in the advancement of medicine, the world is still struggling to combat infectious diseases ^[1]. Mycobacterium tuberculosis (MTB) is responsible for Tuberculosis (TB) infection which primarily affects the lungs (pulmonary TB). However, the disease can also affect some other systems in the human body such as the circulatory system, the central nervous system, the genital-urinary system. TB can be transmitted through a medium including the kiss, speak, cough, sneeze ^[1,2]. It can even affect individuals through the utilization of infected persons unsterilized eating utensils. In some instance, pregnant women who have an active TB can affect the baby in the womb. The actively infected individuals can cause infection but not the latent TB patient. The transmission of TB dependents on the number of infectious droplets expelled by a carrier, the quality of ventilation available and finally, the duration of the individuals exposed to virulence of the MTB strain. The spread of TB can be reduced by isolating the active infectious individual and immediately introducing viable anti-tuberculosis therapy ^[3,4,5]. At the moment, 95% of the world total TB patients of 8 million each year are found in the developing countries. The age bracket that most affected by TB is 15–59. In the developing countries, TB has been identified as the leading death causes in the majority of the Sub-Sahara counties ^[6]. TB has been established as the leading cause of death in sub-Saharan Africa which account for at least 2 million deaths ^[7]. TB in children under the age of fifteen (15) is very critical public health problem since it account for most of the current TB transmission ^[8].

Adaption of modern practice help improves TB control because of factors such as endogenous reactivation, the presence of multi-drug resistant TB, the high rate of HIV incidence in the last two decades. Exogenous re-infection of TB is another concern and very common in Africa. A comprehensive understanding of treatment with respect to the regional transmission of TB is crucial in the fighting of this disease ^[9].

Mathematical modeling in recent times has been identified as an essential tool that provides qualitative information about the epidemiology of many diseases and strategies in controlling them. Several theoretical studies have been undertaking with regard to TB infection. Several integer-order TB models have been constructed and investigated by some authors ^{[10,11,12,13,14]}. The mentioned integer TB models do not predict accurately because they do not have memory effect in order to provide an accurate prediction. However, non-integer models possess memory effect and most of the operators have crossover properties that enhance accurate predictions.

Fractional calculus (FC) is a branch of applied mathematics that generalizes the integer calculus to fractional order ^[15,16]. In recent times, the use of fractional calculus in the scientific community has gained enough attention because of its numerous applications including epidemiology, engineering, water resource management ^{[17,18,19,20,21,22,23,24]}. The use of fractional derivative in modeling epidemiology has become important because the result takes into consideration the memory effect which naturally occurs in several biological models. The reason is that fractional derivative models give the real phenomena associated with the given problem. The fractional of derivatives and integrals give a vivid description of the memory and hereditary characteristics inherent in many materials and other processes ^[25]. Usually, the integer order can provide information about two points which realistically may not be true. The concept of classical fractional-order derivative was proposed by Riemann and Liouville. It was well known that Caputo and Riemann-Liouville have singular kernels. Next, Caputo and Fabrizio in ^[26] presented a new definition of fractional derivative without singular kernel which proved to be good and many researchers are applying. Caputo and Fabrizio ^[27] also investigated the notion of fractional derivative and applications to the hysteresis phenomena. The fractional calculus is now used in mathematical modeling of impulsive fractional functional differential equations. A more interesting study regarding the impulsive fractional functional differential equations and their applications is studied in ^[28].

Recently, Atangana and Baleanu developed a new operator which is based on generalized Mittag-Leffler function where the kernel is non-singular and non-local kernel ^[29]. Numerous studies on non-integer order models in the sense Atangana and Baleanu have been carried out by researchers. For instance, Atangana and Koca in ^[30] studied chaos in a simple nonlinear system using Atangana-Baleanu derivatives in Caputo sense. Atangana and Owolabi in ^[31] developed a new numerical approach for fractional differential equations for solving the system of fractional derivative equations which proved to be efficient. Atangana and Gomez ^[32] presented a detailed analysis of the decolonization of fractional calculus rules: breaking commutativity and associativity to capture more natural phenomena. Khan et al. ^[33] studied the TB dynamics under the framework of the work of Atangana-Baleanu derivative with relapse cases. Bonyah in ^[34] studied a new 5-D hyperchaotic system with four wings by Atangana-Baleanu operator. Khan and Atangana ^[35] studied the Ebola disease with different fractional operators. The comparison of Atangana-Baleanu derivative with Caputo-Fabrizio for the dengue model are studied in ^[36]. Bank data through fractional modeling and their analysis is studied in ^[37]. The dynamics of the chaotic system through Caputo-Fabrizio and the Atangana-Baleanu derivative is studied in ^[38]. The authors studied in ^[39] through different fractional operators of fractional calculus for bank data. Using the Atangana-Baleanu derivative the authors studied the TB dynamics ^[40]. The previously defined fractional operators have some definiens which may or may not correctly investigate the dynamics of such mathematical models that come from science and engineering fields. The Caputo derivative has a singular and local kernel which may not exactly studied the dynamics of a particular problem but these operators are still well known to the researchers and uses for the modeling dynamics. The Caputo-Fabrizio operator was defined without singular kernel. Many researchers used this operator for modeling purposes and still popular among researchers. To have a more precise definition of fractional operator a new operator called Atangana-Baleanu derivative was defined which has a non-singular and non-local kernel and has been used widely for many problems of science and engineering and found it interesting. This new definition is now much famous among researchers around the world. Here, in this work, we consider this newly operator to formulate a new mathematical model for TB dynamics in which we consider the adults and the children as a two groups and present to discuss deeply its mathematical as well as numerical results. This is the first attempt of the authors to have a new mathematical that exploring the children and adults TB dynamics.

It is well known that integer order model does not describes well the dynamics of the disease because there involve history of the disease and their memory. The fractional order models well address the memory effect involve in the disease. At each value of the fractional order parameters we can have a solution but in integer order model we don't have except at the integer case. The difference between two points can be effectively estimated through fractional order models. It is also well known that fractional order models are good for data fitting, where we have variety of choice's for the fractional order parameter. The Caputo operator is singular and local while the AB operator is non-singular and nonlocal. The cross over behavior in the TB model can be addressed well through the AB derivative. Therefore, we considered both the operators and its comparison through graphical results.

To date, there has not been anyone who has investigated the dynamics of TB model with children and adults population using Caputo and Atangana-Baleanu derivative. So, this study investigates a fractional order model in the Atangana-Baleanu sense to explore the spread of TB diseases with in children and adults population. We classify the population into children and adult classes. Based on the risk of transmission, most TB in children is usually not contagious compared to TB in adults ^[8,41]. Hence, the TB model that involves two-age-classes that distinguishes children and adults can indicate a new understanding of TB transmission.

This paper begins by mathematical preliminaries of the fractional derivative. The description of the model with the two-age-class transmission is given in Section 3. The TB model in Caputo derivative with basic properties, calculation of the basic reproduction number, and the numerical result are done in Section 4. The expression of the TB model in Atangana–Baleanu derivative with the existence and uniqueness of the solution, the numerical iterative, and also the numerical simulation are presented in Section 5. The comparison results of both derivatives with various fractional order parameters are shown in Section 6. Finally, the conclusion is shown in Section 7.

2.   Essentials of fractional calculus

We present the details of the fractional operators in the following sections that should be used later in the proposed study.

Definition 2.1. (see ^[16]) For $\alpha > 0$, with $n-1 < \alpha < n, n \in \mathbb{N}$, the fractional derivative in the sense of Caputo is defined to be:

where the symbol $\Gamma(\cdot)$ denotes the gamma function.

The Riemann-Liouville fractional integral is defined by

Definition 2.2. (see ^[29]) Suppose $f\in H^1(0, b)$, $b > 0$, $\alpha \in [0, 1]$, then the Atangana-Baleanu fractional operator in Caputo sense (ABC) can be written as follows:

where $B(\alpha) = 1-\alpha+ \frac{\alpha}{\Gamma(\alpha)}$ is a normalized function with $B(0) = B(1) = 1$ and $E_\alpha$ is Mittag-Leffler function

The integral associated to the ABC derivative in Riemann-Liouville sense is given by,

3.   Description of the model

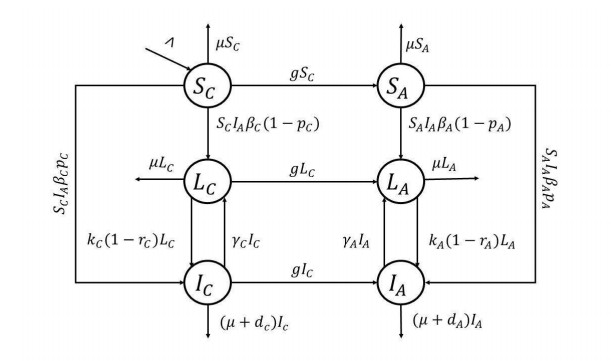
The present section describes the formulation of the mathematical model of TB transmission with two groups of human that is, the children and the adults. We design the model by splitting the population into children ($C$) and the adults class ($A$). Furthermore, each of the classes is divided into three classes, namely, the susceptible classes ($S_C$, $S_A$), the latent TB classes ($L_C$, $L_A$), and the active TB classes ($I_C$, $I_A$), where $S_C$, $L_C$ and $I_C$ represent the susceptible, latent and the active population at any time $t$ respectively, whereas the adults sub-population are respectively shown by $S_A$, $L_A$ and $I_A$. Hence, the total population is $N = S_C + L_C + I_C + S_A + L_A + I_A$. Individuals who are in the latent stage are not infectious and are thus unable to transmit bacteria. We also assumed that the natural death rate of the children and adults population is equal as we consider the average natural death rate of the total population.

The majority of the children with tuberculosis are not infectious to others ^[8,41]. Hence, we assume that only the active TB adults could spread TB with in the population. In this model, it is assumed that children got TB infection by doing contacts with active TB adults. Therefore, the latent TB and active TB children do not spread TB within the population. A small percentage of newly infected individuals from the sub-population is assumed to undergo fast progress directly into the class of active TB, while the rest are latently infected and enter the latent class ^[42]. Furthermore, the TB patients both children and adults cannot recover completely but will enter the latent stage again. Considering these assumptions and facts the following system of evolutionary dynamics of the TB individuals is described through the following systems where the description of the parameters flows and the variables are given in Figure 1.

where the initial values for the model variables are given by

In the above model (3.1), the population of healthy people is generated by the birth rate $\Lambda$ and the growing up rate of children is shown by $g$. The natural death rate of children and adults is denoted by $\mu$. The effective contact rate for both the children and adults is shown by $\beta_C$ and $\beta_A$. The proportion of fast progression of latent class children to infected class children is given by $p_C$ while for adults from latent adult class to infected adult class is by $p_A$. The rate of progression from latent to infected class for the children compartment is shown by $k_C$ while for the adults infection progression from latent to infected class is given by $k_A$. The rate of effective therapy for children and adults are shown respectively by $\gamma_C$ and $\gamma_A$. The rate of effective chemoprophylaxis for children and adults are shown by $r_C$ and $r_A$ respectively. Natural death from TB disease in children infected class is given by $d_C$ while for the adults with TB infection by $d_A$. The description of the parameters for the TB model is set out in Table 1.

The model (3.1) has the biologically feasible region on $\Omega_1$ with

which is feasible biologically and all the results associated holds for it. It should be noted that the parameters involved in the model (3.1) are associated to humans so it is non-negative and the region shown by $\Omega_1$ is positive invariant for the described model (3.1) above. The region shown for the model (3.1) below is well-posed and the entire solutions for the initial values belonging to $\Omega_1$, remains in $\Omega_1$ for every time $t \geq 0$.

Next, in the following section, we explore the TB model in Caputo sense. We apply the definitions of Caputo operator described in above section, and apply it on our model (3.1) and present the results associated to it in the following section in details.

4.   A Caputo model

This section present a TB model with two groups of humans which is shown in (3.1), by applying the Caputo derivative on it. The fractional order model of TB transmission with two-age-class in the Caputo sense is given by:

where $\alpha$ represents the fractional order and $0 < \alpha\leq 1$. The initial values for the model variables in fractional order model (4.1) are given by,

4.1.   Non-negative solutions

This section deals with the positivity of the model solution in the Caputo derivative. We assume that the initial condition of the model (4.1) is non-negative. Let us consider

Here, recalling the important concept given in ^[43] to prove our result.

Lemma 4.1. (see ^[43]) Suppose that $f(t) \in \mathrm{C}[a, b]$ and ${}^CD^\alpha_t f(t) \in \mathrm{C}[a, b]$, for $0 < \alpha \leq 1$, then we have

with $a\leq \xi \leq t$, $\forall t \in (a, b]$.

Corollary 4.2. Consider that $f(t) \in \mathrm{C}[a, b]$ and ${}^CD^\alpha_t f(t) \in \mathrm{C}[a, b]$, for $0 < \alpha \leq 1$. Then if

(1) $^CD^\alpha_t f(t) \geq 0, \forall t \in (a, b)$, then $f(t)$ is non-decreasing.

(2) $^CD^\alpha_t f(t) \leq 0, \forall t \in (a, b)$, then $f(t)$ is non-increasing.

Now, we state the main theorem.

Theorem 4.3. A unique solution exists for $x(t) = (S_C, L_C, I_C, S_A, L_A, I_A)^T$ of the model (4.1) and the solution will be in $\Omega_2$. Additionally, the solution is non-negative.

Proof. Using Theorem 3.1. and Remark 3.2. of ^[44], it is easily to prove the solution existence and also the uniqueness of the solution of the model (4.1) for all $t > 0$. Next, we will prove the positivity of the solution of the model (4.1). In order to do, we have to prove for every hyperplane bounding the nonnegative orthant, of the field points of the vector $\Omega_2$. It follows from the model given by (4.1), we have

By using Corollary 1, the model solution remains in $\Omega_2$.

Thus, it follows from the results described above the feasible given by $\Omega_2$ is positively invariant for model (4.1).

4.2.   Model fixed points

We present here the possible fixed points of the fractional model given by (4.1) and then, we obtain at these possible equilibrium points the stability analysis of the model. For the given model (4.1), there exists two possible equilibrium points that is, the disease free and the endemic equilibrium. We can obtain these equisetum points by setting the time rate of change equal to zero of the model (4.1) and is given by:

We have the following expression,

At the disease free equilibrium, denoted by $E_{01}$, we have from (4.2),

The endemic equilibrium of the model (4.1) is given by $E_{22} = (S_C^*, L_C^*, I_C^*, S_A^*, L_A^*, I_A^*)$ where

The endemic equilibrium $E_{22}$ exists if $\gamma_A + \mu + d_A > \beta_A p_A S_A^*$.

In order to find the basic reproduction number $\mathcal{R}_0$, we consider the method in ^[45] and the matrices are given by

The basic reproduction number is the spectral radius of $\rho(FV^{-1})$ and is given by

where

where

where $S^0_C$ and $S^0_A$ represent the disease-free equilibrium (DFE).

Next, we show the stability of the system at the disease-free case, we follow the following theorem.

Theorem 4.4. For any $p_1, p_2\in \mathbb{Z},$ such that $gcd(p_1, p_2) = 1$. Let $\alpha = (\frac{p_1}{p_2})$ and consider $M = p_2$, then the DFE of the system (4.1) is locally asymptotically stable $(LAS)$ if $|arg(\lambda)| > \frac{\pi}{2M}$, for all roots $\lambda$ of the characteristic Eq. (4.7) of the matrix $J_{E_{01}}$.

Proof. At the disease free equilibrium $E_{01}$, the Jacobian matrix is given by

We obtain the characteristics equation associated to $J(E_{01})$, given by

The arguments of the roots of the equation $\lambda^{p_1}+\mu = 0$, $\lambda^{p_1}+\mu+g = 0$ are as follow:

In Eq. (4.9), the roots are negative, i.e., $-\mu, -(\mu+g)$, while the rest are computed from

where

where $C_1 = \left(d_A \left(k_A \left(1-r_A\right)+\mu \right)+\mu \left(\gamma _A+k_A \left(1-r_A\right)+\mu \right)\right)$,

$C_2 = \left(d_C \left(k_C \left(1-r_C\right)+g+\mu \right)+(g+\mu) \left(\gamma _C+k_C \left(1-r_C\right)+g+\mu \right)\right)$.

The function $Q(\lambda)$ will give eigenvalues with negative real part if $b_i > 0$ for $i = 1, 2, 3, 4$ and $b_1b_2b_3 > b^2_1b_4+b^2_3$. All $b_i > 0$ when $\mathcal{R}_0 < 1$ and the conditions $b_1b_2b_3 > b^2_1b_4+b^2_3$ ensure the stability of the disease free case when $\mathcal{R}_0 < 1$. If ${\cal{R}}_{0} < 1,$ then the necessary condition fulfil for all the roots of characteristics equation i.e., $|arg(\lambda)| > \frac{\pi}{2M}$. Thus the DFE is $LAS$ for ${\mathcal{R}}_{0} < 1$.

The following subsection explore the numerical simulation of the Caputo model.

4.3.   Numerical simulation for Caputo model

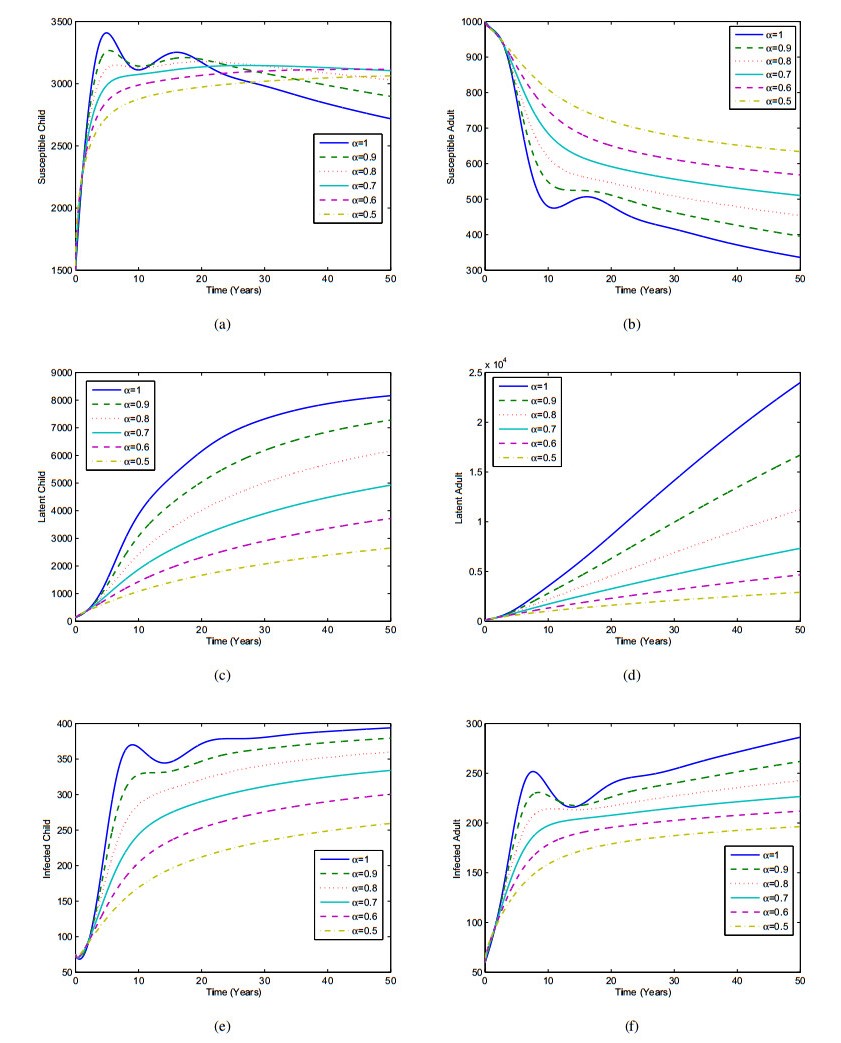
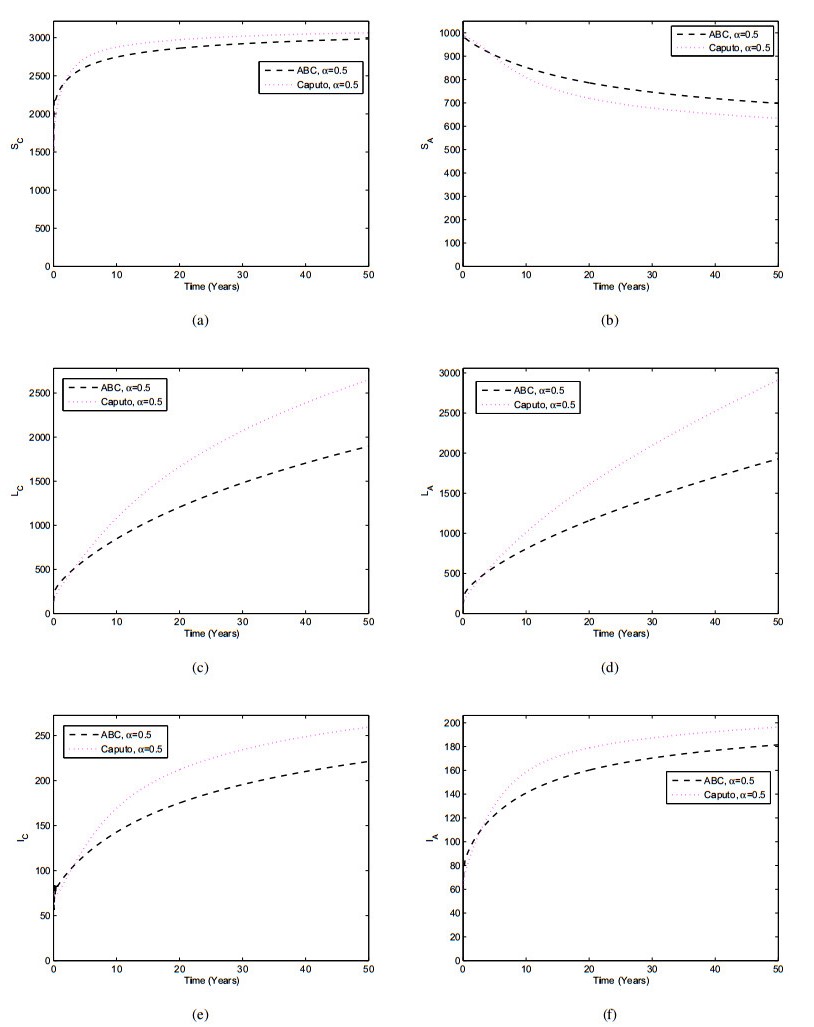
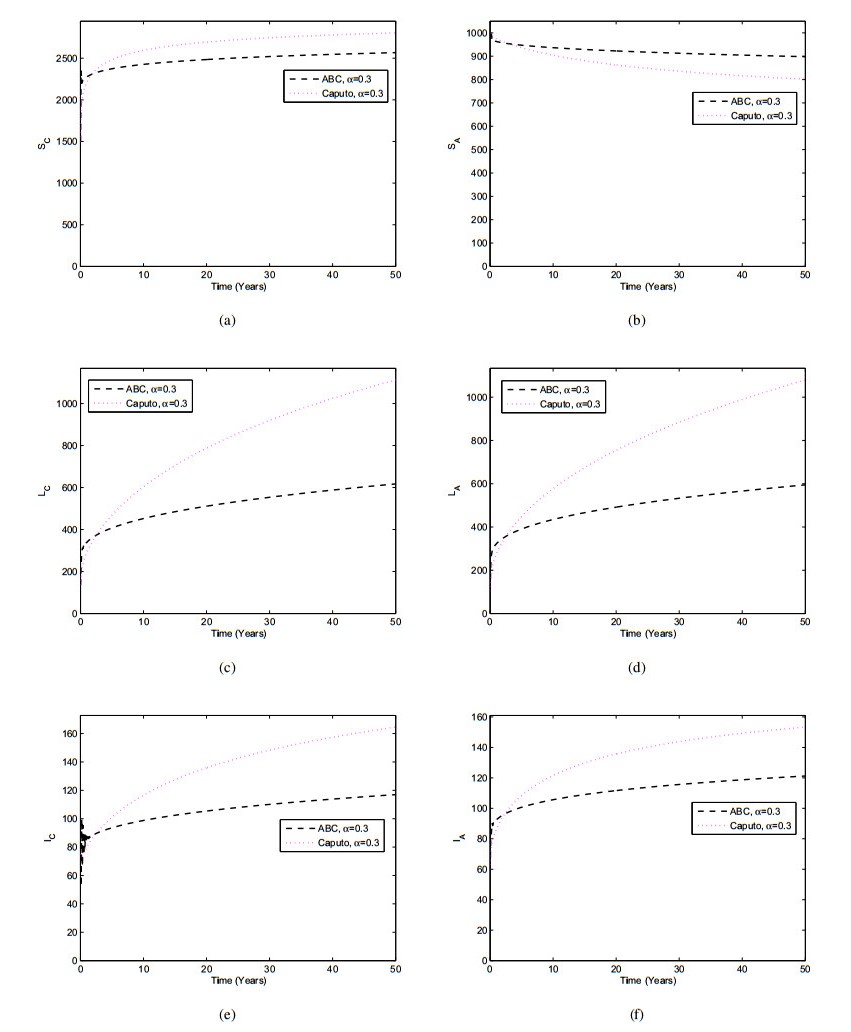
The aim of this section is to discuss a numerical simulation of the model (4.1). The simulation is done with several fractional order values to determine population dynamics in the model. The numerical results of the Caputo derivative are obtained by the Predictor-Corrector method ^[46,47]. Parameters values used in these simulations are set out in Table 2. We take the initial condition $S_C(0) = 1500, L_C(0) = 135, I_C(0) = 75, S_A(0) = 1000, L_A(0) = 103$ and $I_A(0) = 60$. Here, we use 50 years for the time horizon. The simulations are conducted with different values of the order of the fractional derivative $\alpha = 1, 0.9, 0.8, 0.7, 0.6$ and $0.5$. We have the simulation results of the TB model (4.1) in Figure 2. In this case the value of $R_{0}$ is $R_{0} = 91.5021 > 1$, which indicates the disease will persist in the population. We can observe in Figure 2 that as the values of $\alpha$ decrease, the individuals infected with TB decreases whereas the population of susceptible individuals increases.

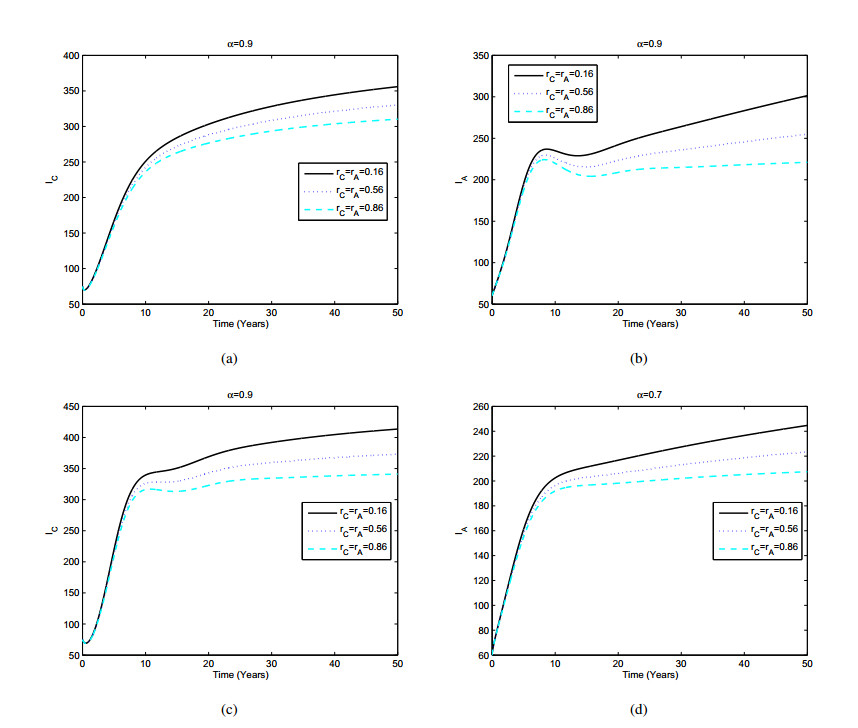
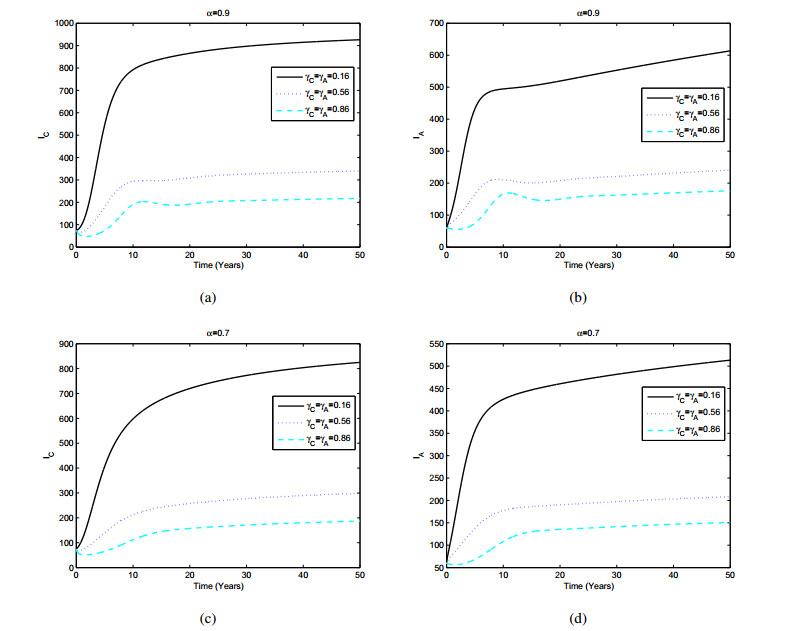
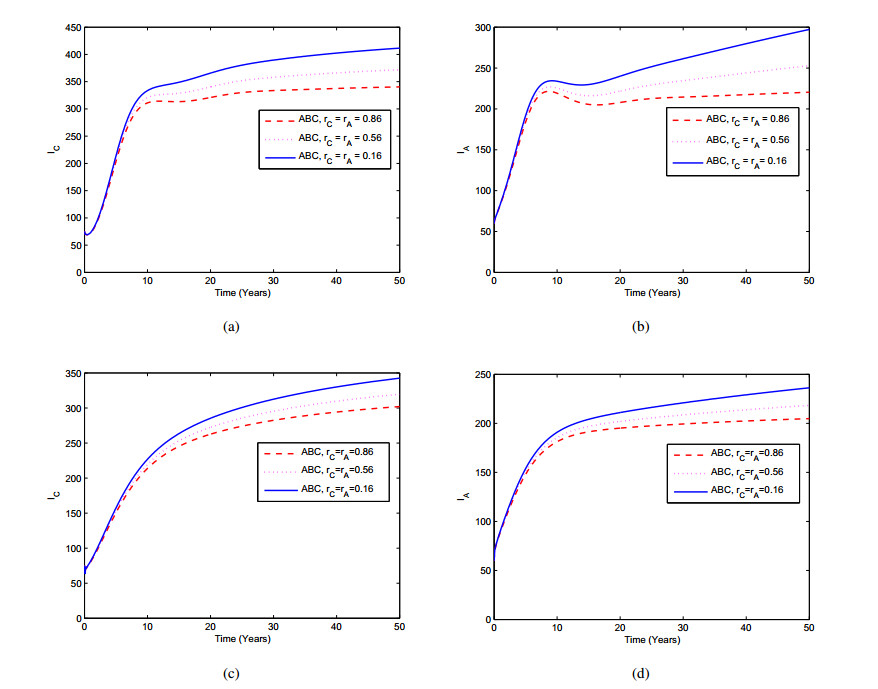
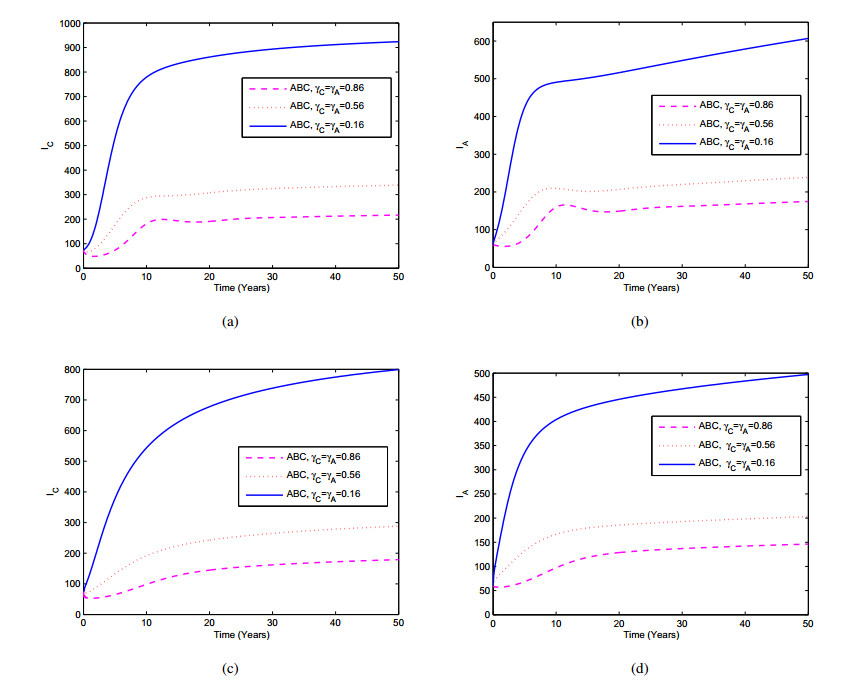
Next, we will see the effect of chemoprophylaxis and treatment on the active TB populations in both children and adults. The numerical simulation is deployed by varying the effectiveness of chemoprophylaxis ($r_C, r_A$) and treatment ($\gamma_C, \gamma_A$). In Figures 3, 4, we display the dynamic of the active TB populations for different values of the efficacy of chemoprophylaxis and treatment. For $\alpha = 0.9$, it is shown that the population of the active TB both children and adults have decreased when the efficacy of chemoprophylaxis and treatment have increased. Conversely, when the efficacy of chemoprophylaxis and treatment falls, the population of the active TB both children and adults will rise. The likewise behavior is seen for $\alpha = 0.7$. This shows that chemoprophylaxis and treatment were given to patients with latent stage and active TB respectively can reduce the number of TB infection populations of both children and adults.

Next, we express the model of TB in Atangana-Baleanu derivative where their kernel is non-singular and non-local which best describes the dynamics of real world problem.

5.   TB model in the Atangana–Baleanu sense

The newly derivative called the Atangana-Baleanu derivative where their kernel is non-local and non singular is considered here to apply on our model presented in (3.1). We follow the definition described above and have the following representation:

with some appropriate initial conditions. For the TB fractional model in Atangana-Baleanu form is studied further to obtain their existence and uniqueness. We have the following:

5.1.   The existence and uniqueness of the solution

Here, we display the uniqueness and existence results associated to the AB model (5.1). In order to show the results for the model we follow the results of the fixed-point theory. We first write the (5.1) in the form shown below,

In system (5.2), $u(t) = (S_C, L_C, I_C, S_A, L_A, I_A)$ is simply a vector having the state variable and $G$ is therefore a continuous vector function given as

and $u_0(t) = (S_C(0), L_C(0), I_C(0), S_A(0), L_A(0), I_A(0))$ representing the state variables initial conditions in vector form. The above function namely, $G$ satisfies the condition of Lipschitz continuity and can be described as below:

The following result is provided in order to show the model existence and their solution as well as uniqueness for the model (5.1).

Theorem 5.1. (Existence and uniqueness) The model given by (5.2) has the unique solution provided that the following condition satisfy,

Proof. To prove the above statement, we need to use the fractional integral associated to the Atangana-Baleanu model given by (2.4). The application of this integral on (5.2), leads to the following non-linear voltera integral equation:

We assure that $J = (0, T)$ and take into consideration the operator $\phi: \mathrm{C}\left(J, \mathbb{R}^6\right)\rightarrow \mathrm{C}\left(J, \mathbb{R}^6\right)$ defined by

Equation (5.5) turns to

The supremum norm on $J$, $\|\, .\, \|_J$ is $\|u(t)\|_J = \sup_{t\in J}\| u(t) \|, \, u(t) \in \mathrm{C}$.

Obviously, $\mathrm{C}\left(J, \mathbb{R}^6\right)$ along the norm $\|\, .\, \|_J$ present a Banach space. Additionally, we can demonstrate simply the following inequality

with $u(t) \in \mathrm{C}\left(J, \mathbb{R}^6\right), \, D(t, \varepsilon) \in \mathrm{C}\left(J^2, \mathbb{R} \right)$.

In a way that

Applying the definition of $\phi$ stated in (5.7), we derive

Furthermore, using the principles of triangular inequality and Lipschitz condition stated in (5.3) couple with the results in (5.8) we get the following after some algebraic simplification.

Thus, we eventually have

where

Therefore, the operator $\phi$ will become a contraction if condition (5.4) holds on $\mathrm{C}\left(J, \mathbb{R}^6\right)$. As a result of Banach fixed point theorem, system (5.2) possesses a unique solution.

5.2.   Numerical scheme for the Atangana - Baleanu model

This section derive the numerical scheme of the TB model in the ABC form which given by Eq. (5.1) using the method in ^[52] by using Adams-Bashforth method. By using the same procedure in ^[52], we write (5.1) to the following

By utilizing the fundamental theorem of fractional calculus, we convert (5.9) to fractional

At $t = t_{n+1}, \, n = 0, 1, 2, ...,$ we have

The integral in Eq. (5.11) is approximated through the two-point interpolation polynomial. Hence, we have the iterative scheme for the TB model (5.1). After some calculations, we finally obtain the approximation solution as

Next, we present the simulation result of the TB model (5.1) using the numerical scheme.

5.3.   Numerical simulation of Atangana-Baleanu model

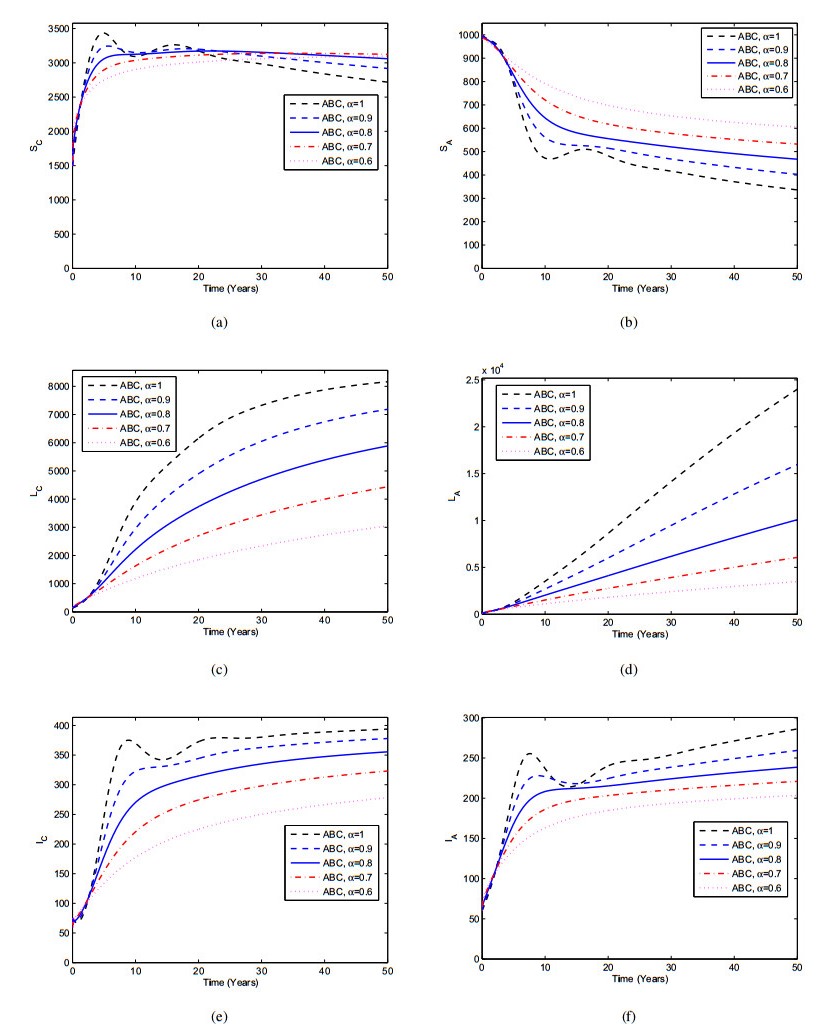
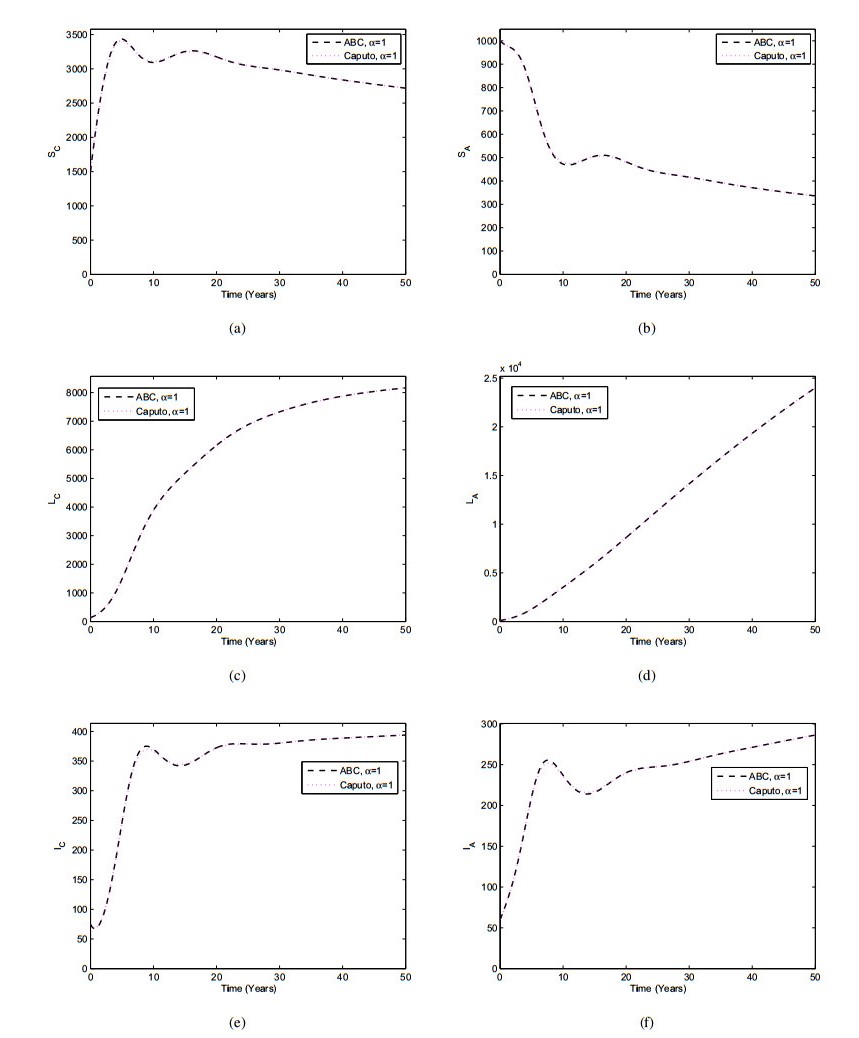
This section provides the simulation results of Atangana-Baleanu model (5.1) using the iterative scheme obtained in (5.12). The parameter values listed in Table 2 are for obtaining the numerical results 2. The simulation results are shown in Figure 5 by considering different values of $\alpha = 1, 0.9, 0.8, 0.7$ and $0.6$. In Figure 5, we can see that by decreasing the values of $\alpha$, the population of infected compartments decreases, while the susceptible population increase.

In Figures 6 and 7, we present the effect of the efficacy of chemoprophylaxis ($r_C$ and $r_A$) and treatment ($\gamma_C, \gamma_A$) on the TB transmission for different values of $\alpha$. From Figure 6, it can be seen that as the chemoprophylaxis strategy increase, the infected TB in both children and adults population decrease. From Figure 7, it is shown that as the treatment strategy increase, the infected TB in both children and adults population decrease significantly.

6.   Comparison of operators

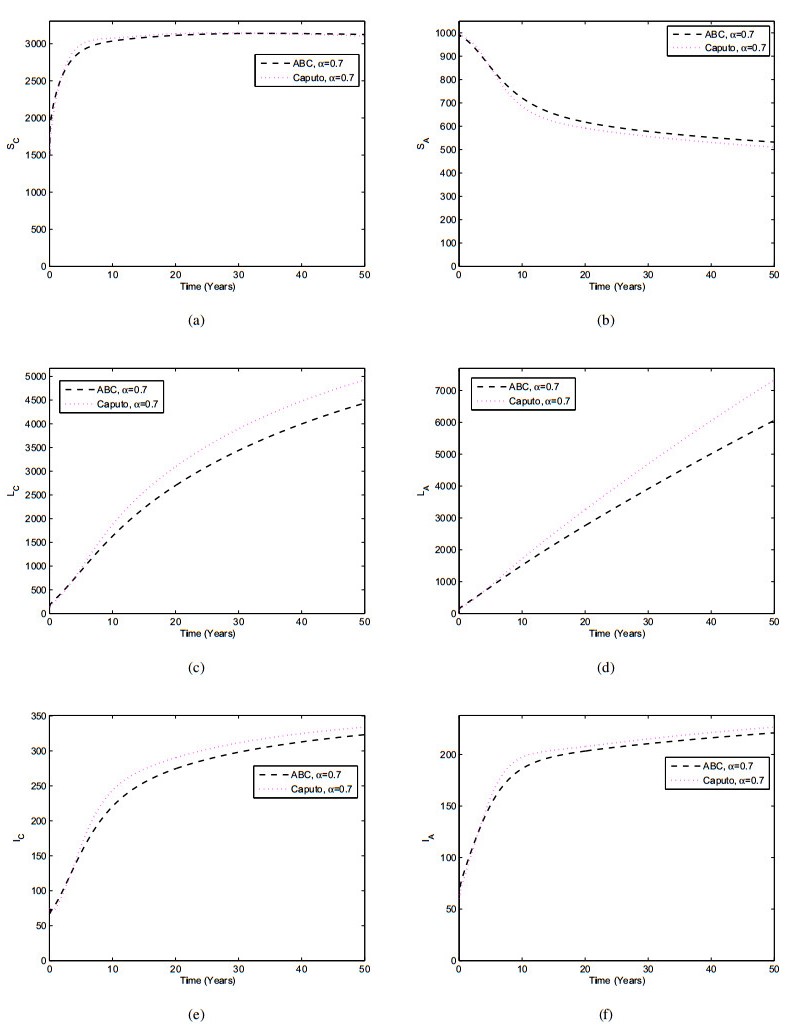
This present section demonstrates the comparison of the Caputo and Atangana-Baleanu operators graphically. The parameter values used in these simulations are given in Table 2. In order to have a comparison of these two operators we considered many values of $\alpha = 1, 0.7, 0.5, 0.3$ and the results were displayed Figures 8–11. It can be seen in Figures 8–11 that there exists a significant difference in the dynamical behavior of the TB infected population when the values of $\alpha$ decrease within both fractional operators. From these figures, we see that Atangana-Baleanu derivative give faster decreases in the results compare to the Caputo derivative when the fractional order parameter decrease for the reduction of TB infection. This comparison section demonstrate the effectiveness of the Atangana-Baleanu derivative over the Caputo derivative.

7.   Conclusion

The findings reported here shed new light on the fractional-order model with Caputo and Atangana-Baleanu derivative to investigate the spread of TB with children and adults population. Brief mathematical results for the TB model are investigated. The basic reproduction number of the Caputo model and its equilibrium are obtained and presented the results. Each model is studied independently in the fractional operators of Caputo and Atangana-Baleanu. We then performed the numerical simulations of the Caputo model type for different values of the fractional-order using the predictor-corrector method. Then, we apply the fractional Atangana-Baleanu operator to the model and analyzed and obtained the associated results. We proved the uniqueness and existence of the Atangana-Baleanu model. The numerical simulation of the Atangana-Baleanu model was conducted using the Adams–Bashforth scheme. We further presented the graphical results of Atangana-Baleanu model for various fractional order parameters. A comparison of the proposed operators graphically presented. These graphical results for comparison show that the Atangana-Baleanu results are more appropriate for the better decrease in infection while the Caputo is less. We conclude from graphical results that increasing chemoprophylaxis and treatment rates then the TB infective both children and adult cases can be reduced. The graphical results show that a decrease in fractional order parameter causes a significant decrease in the infective TB population. Therefore, the present work is a novel analysis on the TB dynamics and will be more useful for the readers and public health authorities. In future work the TB age fractional model can be considered in the light of fractional impulse model and the results can be compared with non-impulse TB model, stated in ^[53,54,55]. This is important because the impulse effect is attracting the receiving considerable attention and eliciting widespread interest in epidemiological models.

Acknowledgements

Part of this research is financially supported by Unversitas Airlangga 2018.

Conflict of interest

All authors declare no conflict of interest.