Quasi-synchronization of nonlinear systems with parameter mismatch and time-varying delays via event-triggered impulsive control

1.   Introduction

The collaborative behavior of dynamical systems has been gaining increasing attention from academic researchers over recent decades. Synchronization as an important and interesting collaborative behavior often occurs in biological systems, social systems and neural networks. Synchronization can find many potential applications in multi-agent systems ^[1], secure communications ^[2], drones, and image encryption. Synchronization phenomenon widely exists and affects various industries and therefore, it is necessary to conduct research on synchronization. How to design effective control methods to make the system achieve synchronization is the current research focus in the control area.

There are various control methods for researching synchronization, such as sampling control ^[3], pinning control ^[4,5], adaptive control ^[6], continuous-time feedback control ^[7], impulsive control (IC) ^[8], event-triggered control (ETC) ^[9], intermittent control^[10], and the combinations of these with other control methods. The control methods mentioned above take into account both environmental and practical constraints while ensuring that the required performance is achieved. Among them, IC is superior in efficiency and has a wider range of applications, and it has been used in network stability and synchronization ^[11,12] research. For example, in ^[13], the prescribed-time synchronization problem and topology identification for complex networks of piecewise-smooth systems were studied under hybrid impulse control. In ^[14], the practical synchronization problem of delayed neural networks with external disturbance and delayed impulses were studied under hybrid impulse control. Besides, IC provides control input to the system at discrete time points, which can overcome the restrictions of the continuous control methods and reduce the waste of communication resources. Therefore IC is a promising strategy that is getting more and more attention^[15,16,17].

Time-triggered impulsive control (TTIC) was the approach used in most of the research methods mentioned above, where the impulsive instant follows a predetermined time sequence. Exponential synchronization of the network was studied by designing an impulsive controller ^[18], but TTIC leads to a waste of resources–some control inputs were not necessary when the system achieved the demanded performance. In order to avoid frequent updates and reduce the communication loads and computational cost, ETC was proposed. ETC is able to overcome these drawbacks because its event-triggered moments are designed according to the system states, and control signals are sent only when required, which makes it more efficient than other control methods^{[19,20,21,22,23]}. For example, in ^[24], a hybrid ETC approach was proposed to investigate the prescribed-time synchronization problem for complex dynamic networks of piecewise smooth systems. In ^[25], a memory-based quantized dynamic ETC strategy was proposed to investigate the practical finite-time synchronization problem for Lur'e systems with actuator faults and performance constraints. ETC is more preferred in industrial applications due to its superiority in saving communication costs and resource utilization^[26,27,28]. Taking into account the advantages of ETC and IC, event-triggered impulsive control (ETIC) was proposed. In this method, the impulsive instant is also an event-triggered moment, and the impulsive instant is no longer triggered by a predetermined time, but determined by a state-dependent trigger function. An event will be triggered only when the control error signal exceeds the designed threshold value ^[29]. The ETIC mechanism demonstrates significant advantages across various controlled systems ^[11,19,30].

In the real world, it is inevitable to have coupled dynamical systems with parameter mismatch, even if the majority of current research on synchronization centers around systems with matching parameters. For instance, the parameters of memristor neural networks (MNNs) depend on their system states^[8]. Different initial conditions may lead to heterogeneity in the parameters of MNNs, thus the system cannot achieve complete synchronization. Consequently, it is necessary to study the weak cooperative behavior generated by the parameter mismatch system^[18,31]. There are two types of parameter mismatch: function-dependent (or structure-dependent) parameter mismatch (FDPM) and state-dependent parameter mismatch (SDPM). Since the parameters of MNN are state-dependent variables, MNNs can be regarded as a switching system, and different initial values may lead to asynchronous switching. ^[18,32] analyzed the parameter mismatch of this type (SDPM). Another type of parameter mismatch (FDPM) was analyzed in ^[33], where the drive-response system may have a different parameter structure. As far as we know, most of the existing achievements are about the parameter mismatch synchronization of MNNs, so our paper will investigate the quasi-synchronization (QS) of nonlinear systems with parameter mismatch and time-varying delays. A characteristic of QS is that its error does not exceed a non-zero bound^[18,31,34]. However, the impulsive instants in these articles focus on TTIC, which may lead to resource waste. Beyond control strategies, the generalization of system models to yield more universal results is also a focal point of research. In recent years, many papers have considered time delay ^[35], which is a phenomenon that indicates that the state of a system depends on both its current and past states. It is widely discovered in various network systems. As a common system disturbance, the interference of delay may change the initial dynamic behavior of the network model, for instance, when the delay intervened to a stable neural network, the neural network produced a chaotic attractor ^[36]. Therefore, it is valuable and important work to account for time delay in system analysis, especially for the synchronization dynamics of delayed systems.

Based on the brief summary and discussion above, this paper aims to investigate the QS of nonlinear systems with parameter mismatch and time-varying delays by using ETIC. There are three primary challenges and difficulties in our study: the first challenge is how to handle the system delay term and ETC input term; the second difficulty is how to handle the parameter mismatch system and derive the QS conditions; the third difficulty is how to ensure that we can avoid Zeno behavior in the trigger moment and calculate the minimum of the trigger interval. Our proposed method effectively resolves these challenges. The following are the main contributions of this paper.

(1) Different from^[33], this paper considers the time-varying delays in the system. In contrast to the synchronization of the same structure^[37], this paper considers the QS of nonlinear systems with parameter mismatch and time-varying delays, which are prevalent in practical applications.

(2) The control method is different from the traditional TTIC in ^[38]. Our approach integrates IC and ETIC together to address the QS of drive-response systems. The impulsive instants are event-triggered, which greatly reduces the communication costs and resource consumption.

(3) Under the proposed ETIC strategy, an accurate QS error bound is derived by using the comparison principle of impulsive systems and the formula for variable parameters. Additionally, we ensure that the Zeno behavior at impulsive instant is avoided.

Notations: $\mathfrak{R}^n$ denotes $n$-dimensional Euclidean space and $\mathfrak{R}^{n\times m}$ denotes $n \times m$-dimensional Euclidean space. For a vector or matrix, $\left \| \cdotp \right \|$ stands for its 2-norm. For any vector $z$ or matrix $\mathcal{Z}$, $z^T$ or $\mathcal{Z}^T$ denotes that its transposition. For matrix $\mathcal{Q}$, $\mathcal{Q} > 0$ denotes $\mathcal{Q}$ is a positive definite matrix. $\mathfrak{R}^+$ denotes the set of positive real numbers and $\mathcal{Z}_+$ denotes the set of positive integers. $C\left (\left [ -\rho, 0 \right ], \mathfrak{R}^n\right)$ (abr. $PC_\rho$) represents a space composed of the continuous function mapping $[ -\rho, 0 ]$ into $\mathfrak{R}^n$. $\mathcal{I}$ represents the identity matrix of the appropriate dimension.

2.   Preliminaries and model description

2.1.   Preliminaries

The general nonlinear impulsive differential delayed system is considered as follows:

where $\varpi\left(t\right) \in \mathfrak{R}^{n}$ denotes the state variable of the system and $\dot{\varpi}\left(t\right)$ is the upper-right derivative of $\varpi\left(t\right)$. For $t\geq t_0$, define $\varpi_t\left(s\right) = \varpi \left(t+s\right)$, $\varpi_t \in PC_\rho$, where $\rho$ is the upper bound of the time-varying delays $\rho \left(t\right)$. For all $t, k$, we assume $\mathcal{J}\left(0\right) = \mathcal{G}\left(0\right) = 0$, and $\delta\left(s\right) \in PC_ \rho$ is the initial value. The time sequence $\left\lbrace t_k\right\rbrace$ is the impulsive instant generate by ETIC. The system jump will be activated at the impulsive instant $t_k$, where

We assume system (2.1) is left continuous at every impulsive instant $t_{k}$, namely, $\varpi\left(t_{k}\right) = \varpi \left(t_k^{-}\right)$, $\forall k\in \mathcal{Z}_{+}$. We assume that functions $\mathcal{J}, \mathcal{G}$ satisfy appropriate conditions such that the solution $\varpi \left (t\right)$ exists in the relevant time interval, which will be set later in the assumption.

2.2.   Model description

Let

be the drive system, where $\zeta \left(t\right) = \left(\zeta _1\left(t\right), \zeta _2\left(t\right), \dots, \zeta _n\left(t\right)\right) ^T \in \mathfrak{R}^n$ stands for the state variable of drive system, with initial condition $\zeta\left(s\right) = \left(\delta_1\left(s\right), \delta_2\left(s\right), \dots, \delta_n\left(s\right) \right) ^T\in PC_\rho$, $\sigma \in C\left (PC_\rho, \mathfrak{R}^n\right)$, is a nonlinear function, and $\mathcal{A}_1, \mathcal{B}_1 \in \mathfrak{R}^{n\times n}$ are constant matrices.

The response system of (2.2) is described as

where $\tilde{\zeta }\left (t\right) = \left(\tilde{\zeta }_1\left (t\right), \tilde{\zeta }_2\left (t\right), \dots, \tilde{\zeta }_n\left (t\right)\right) \in \mathfrak{R}^n$ stands for the state variable of the response system, with the initial condition $\tilde{\zeta }\left (s\right) = \psi \left(s\right) = \left(\psi _1\left(s\right), \psi _2\left(s\right), \dots, \psi _n\left(s\right)\right) \in PC_\rho$. $\mathcal{U}\left(t\right)$ is the control input and $\mathcal{A}_1\neq \mathcal{A}_2, \mathcal{B}_1\neq \mathcal{B}_2$, i.e., drive-response systems (2.2)-(2.3) have their own different dynamical behavior if $\mathcal{U}\left(t\right) = 0$.

The controller $\mathcal{U}\left(t\right)$ designed in this paper is shown as below:

where $\zeta \left (t_k\right)\neq \tilde{\zeta }\left (t_k\right)$, $\mathcal{K}$ and $\mathcal{C}$ are the ETC gain matrix and IC gain matrix, respectively. The sequence $\left\lbrace t_k, k\in Z_+\right\rbrace$ are impulsive instants which are generated by the designed triggering law designed later in this paper.

Define the synchronization error $\eta \left(t\right) = \tilde{\zeta }\left (t\right)-\zeta \left (t\right)$ between system (2.2)-(2.3), and $\eta \left(t\right) = \left(\eta _1\left(t\right), \eta _2\left(t\right), \dots, \eta _n\left(t\right)\right) ^T$, with initial condition $\eta \left(s\right) = \psi \left(s\right) -\delta\left(s\right) \in PC_\rho$. Then

Then

which represents the parameter mismatch caused by different structures.

Remark 1. Under the ETIC strategy, the control action of (2.4) is determined by the state error of system (2.2)-(2.3). Control actions persist in the presence of state error, and they stop when the error is zero. QS is different from complete synchronization, and a drive-response system with the same structure can achieve complete synchronization under an appropriate controller. However, if the drive-response system has a different structure, the state error always exists, which means that the controller will always act on the error system ^[18]. Although the drive-response system with FDPM cannot achieve complete synchronization in this paper, an appropriate controller can maintain the error within a certain range. Therefore, the QS of the drive-response system will be investigated in this paper.

The following are the assumptions proposed in this paper.

Assumption 1 (^[39]). Suppose that the state $\zeta \left(t\right)$ of the drive system for any initial condition $\delta\left(s\right) \in C\left (\left [ -\rho, 0 \right ], \mathfrak{R}^n\right)$ is bounded, i.e., there exists $\Gamma\left(\delta\left(s\right) \right)$ such that

Assumption 2. Suppose the nonlinear function $\sigma \left(\cdot\right)$ satisfies the Lipschitz condition, and there exists constant $p > 0$, for $\forall \zeta _1, \zeta _2 \in \mathfrak{R}^n$, such that

Assumption 3. There exists a constant $P > 0$, such that function $\sigma \left(\cdot\right)$ is bounded, i.e.,

Remark 2. The assumptions mentioned above are reasonable. Assumption 1 is a tenable assumption ^[39]. When the system delay is within an appropriate range, the system can satisfy the bounded condition. The drive chaotic system with finite evolution is widely used in research work. Assumptions 2 and 3 are the Lipschitz conditions that are satisfied by most linear and nonlinear continuous functions.

We assume $\mathcal{N}\left(\zeta \left(t\right), \zeta\left(t-\rho \left (t\right) \right) \right) = \triangle \mathcal{A} \zeta \left(t\right)+\triangle \mathcal{B} \sigma \left (\zeta \left(t-\rho \left (t\right)\right)\right)$, according to Assumptions 1 and 2, and it can be inferred that there exists a constant $\alpha$, so that

i.e., $\mathcal{N}\left(\zeta \left(t\right), \zeta \left(t-\rho \left (t\right)\right) \right)$ is also bounded. In addition, according to $\eta \left (t\right) = \tilde{\zeta }\left (t\right)-\zeta \left (t\right)$, we can obtain

With the proposed controllers (2.4) and (2.7), error system (2.5) can be simplified and rewritten in the form below:

Let the state measurement error of error system (2.8) be defined as

and the following triggering law determines the impulsive sequence $\left\lbrace t_k\right\rbrace$:

Obviously, one can select some appropriate positive constants $\alpha_1, \; \alpha_2, \; \tilde{\alpha }$ and gain matrix $\mathcal{K}$ such that $\left (\tilde{\alpha }-{\alpha}_1^{-1}\right)\mathcal{I}-\alpha _2\mathcal{K}\mathcal{K}^T > 0$. Therefore, we always assume that matrix $\left (\tilde{\alpha }-{\alpha}_1^{-1}\right)\mathcal{I}-\alpha _2\mathcal{K}\mathcal{K}^T$ in (2.10) is a positive definite matrix in the following discussion.

Remark 3. To investigate more general parameter mismatch systems, we need $\mathcal{A}_1\neq \mathcal{A}_2$ and $\mathcal{B}_1\neq\mathcal{B}_2$. In fact, the following two special cases are both included in our results. For the case $\mathcal{A}_1\neq \mathcal{A}_2$, and $\mathcal{B}_1 = \mathcal{B}_2$, then $\triangle \mathcal{B} = 0_{n\times n}$, $\left \| \mathcal{N}\left (\zeta \left(t\right), \zeta \left(t-\rho \left (t\right)\right)\right) \right\| = \left \|\triangle \mathcal{A} \zeta \left(t\right) \right \|\leq k_1$. For the case $\mathcal{A}_1 = \mathcal{A}_2$, and $\mathcal{B}_1\neq \mathcal{B}_2$, then $\triangle \mathcal{A} = 0_{n\times n}$, $\left \| \mathcal{N}\left (\zeta \left(t\right), \zeta \left(t-\rho \left (t\right)\right)\right)\right \| = \left \|\triangle \mathcal{B} \sigma \left (\zeta \left(t-\rho \left (t\right)\right)\right) \right \|\leq k_2$, where $k_1, \; k_2$ are positive constants.

Remark 4. The ETIC strategy proposed in this paper combines ETC and IC. In the controller (2.4), IC takes place precisely at the event-triggered instant. Meanwhile, between any two successive impulsive moments, there exists ETC input. The ETC works until the next impulsive $t_{k+1}$. In fact, the ETC can be seen as a bridge connecting the two impulsive items. In the control input of controller (2.4), the first part stands for ETC, and the second part represents IC. This paper proposes an ETIC method that offers better performance and a lower cost of control. Whether impulsive moments are generated depends on the state error within the drive-response systems.

Remark 5. Unlike the conventional impulsive systems discussed in ^[38], which depend on time-triggered mechanisms to determine impulsive instances, the impulsive system (2.8) in this paper employs an event-triggered approach. This methodology significantly minimizes unnecessary information transmission, computational load, and communication overhead.

2.3.   Definitions and lemmas

In this subsection, to analyze the QS of systems (2.2) and (2.3) we will present several definitions and lemmas required for this paper. First, we introduce some fundamental definitions.

Definition 1 (^[2]). A function $\mathcal{L} : \mathfrak{R}^{+}\times \mathfrak{R}^{n}\rightarrow \mathfrak{R}^{+}$ is said to belong to the function class $v$ if it is a locally Lipschitz function and continuous in $\left(t_k, t_{k+1}\right] \times \mathfrak{R}^n$, for $\forall \varsigma \left(t\right) \in \mathfrak{R}^n$, and then

Definition 2 (^[2]). Given a locally Lipschitz function $\mathcal{L} : \mathfrak{R}^{+}\times \mathfrak{R}^{n}\rightarrow \mathfrak{R}^{+}$, its upper-right derivative is defined as:

Definition 3 (^[38]). Drive-response systems (2.2) and (2.3) are said to achieve the QS with error bound $\hat{\epsilon } > 0$. When $t\to +\infty$, if there exists a set $\Omega$, such that for all $\delta\left(s\right), \; \psi \left(s\right) \in PC_\rho$, the synchronization error $\eta \left (t\right)$ converges to $\Omega : = \left \{ \eta \left (t\right)\in \mathfrak{R}^n| \left \| \eta \left (t\right)\right \|\leq \hat{\epsilon }\right \}$, where $\eta \left (t\right) = \tilde{\zeta}\left (t\right)-\zeta \left(t\right)$, $\tilde{\zeta}\left (t\right)$ and $\zeta \left(t\right)$ are the solution of the response system and drive system, respectively.

Definition 4 (^[37]). Impulsive instants $t_k$ have no Zeno behavior if there always exists a positive constant $\varkappa$ such that the trigger interval is greater than it, i.e., $\inf_{k\in N}\left\lbrace t_{k+1}-t_k\right\rbrace \geq \varkappa > 0$.

Next, we state some important lemmas.

Lemma 1 (^[40]). Let $\mu > 0$, for any vectors $x \in \mathfrak{R}^n, \; y \in \mathfrak{R}^n$, and matrix $\mathcal{A}\in \mathfrak{R}^{n\times n}$, and then the following inequality holds:

Lemma 2 (^[41]). Let $w_1\left(s\right)$ and $w_2\left(s\right) \in PC([-\rho, +\infty], \; R^+)$ be jumping discontinuous at $s = s_k, \; s\geq 0$, $w_1\left (s_k^{-}\right)$ and $w_2\left (s_k^{-}\right)$ exist, $w_1\left (s_k\right) = w_1\left (s_k^{+}\right), \; w_2\left (s_k\right) = w_2\left (s_k^{+}\right)$, $0\leq \rho \left (s\right)\leq \rho$. If there exist constants $\pi _1, \; \pi _2 > 0, \; \beta > 0$, such that

and $w_1\left (s\right)\leq w_2\left (s\right)$ for $-\rho \leq s\leq 0$, then $w_1\left (s\right)\leq w_2\left (s\right)$ for $s > 0$.

3.   Main results

In this section, the ETIC mechanism will be used to investigate the QS between (2.2) and (2.3) with time-varying delays. Additionally, we rule out the Zeno behavior of the impulsive instant in the ETIC mechanism.

Theorem 1. Assume that Assumptions 1–3 hold and under the control law (2.10), if there exists constant $\beta_1 < 0$ such that $\mathcal{A}_2+A_2^T+\mathcal{B}_2 \mathcal{B}_2^T+2\mathcal{K}+\tilde{\alpha }\mathcal{I}-\beta_1 \mathcal{I} < 0$, and there exists constant $\lambda_2$, such that $0 < \lambda _2 < 1$, $\left (\mathcal{I}+\mathcal{C}\right)^T\left (\mathcal{I}+\mathcal{C}\right)-\lambda _2\mathcal{I} < 0$. Then, the drive system (2.2) and response system (2.3) can achieve QS. The synchronization error $\eta \left (t\right)$ converges to

when $t\rightarrow \infty$, where $\beta _2 = p^2\lambda _{max}\left (\mathcal{I}\right)$, $0 < \lambda_3\leq-\frac{ln\lambda _2}{m_1}-\beta _1$, $m_1\geq \sup\left\lbrace t_{k+1}-t_k\right\rbrace > 0$.

Proof. We choose the nonnegative Lyapunov function for error system (2.8) as:

Evidently $\mathcal{L}\left (t, \eta \left (t\right)\right)$ belongs to function class $v$. Along the error system (2.8) calculate the right-upper derivative of $\mathcal{L}\left (t, \eta \left (t\right)\right)$, for $t\in \left(t_k, t_{k+1}\right)$, and we can obtain

We obtain the following inequalities by utilizing Assumption 1 and Lemma 1:

Then, substituting the above simplification into (3.3), we have

According the triggering law (2.10),

We derive from (2.6), (3.4), and (3.5) that

Furthermore, when $t = t_k$, according to (2.8) and (3.2), one has

Suppose $w\left(t\right)$ is a unique solution of the following delayed impulsive comparison system, $\forall \delta > 0$. Therefore, the corresponding comparison system for (3.6) and (3.7) is as follows:

For $t\geq 0$, by using Lemma 2 we have

Using the variable parameter formula for (3.8), we can describe $w\left(t\right)$ in terms of

$\mathcal{H}\left(t, s\right)$ is the Cauchy matrix of system $\dot{w}\left (t\right) = \beta _1w\left (t\right), w\left ({t}_{k}^{+} \right) = \lambda _2w\left (t_k\right)$, and additionally, through the induction,

Due to $\beta_1 < 0$ and $0 < \lambda_2 < 1$, $\forall k \in N$, since $\sup_{k\in N}{\left\lbrace t_{k+1}-t_k\right\rbrace < \infty }$, thus there exists constant $m_1$ such that $0 \leq \sup_{k\in N}{\left\lbrace t_{k+1}-t_k\right\rbrace \leq m_1}$, and there exists $0 < \lambda_3\leq-\frac{ln\lambda _2}{m_1}-\beta _1$ such that

Substituting (3.11) into (3.10), then

where $\iota = \frac{1}{\lambda _2}\sup_{-\rho \leq t\leq 0}{\left \| \eta \left (t\right)\right \|^2}$. Define

By the continuity of function $\mathcal{M}\left(\hbar \right)$, and $-\left (\frac{ln\lambda _2}{m_1}+\beta _1\right) > \frac{1}{\lambda _2}\beta _2 > 0$, we have $\; \mathcal{M}\left (\infty \right) > 0$, $\mathcal{M}\left (0\right) = \frac{ln\lambda _2}{m_1}+\beta _1+\frac{1}{\lambda _2}\beta _2 < 0$, and $\dot{\mathcal{M}}\left (\hbar \right) = 2+2\frac{1}{\lambda _2}\beta _2\rho {e}^{2\hbar \rho } > 0$. Therefor, there exists a unique positive solution $\hbar$ such that $\mathcal{M} \left (\hbar \right) = 0$.

Evidently, $\hbar > 0, \; \delta > 0, \; \alpha _1\alpha ^2 > 0$, and $\frac{1}{\lambda _2} > 1$, for $t \in [-\rho, 0]$, and then

For all $t > 0$, we will demonstrate that the following inequality holds:

If (3.14) is incorrect, then there exists a constant ${t}^{*} > 0$, such that

According to (3.12) and (3.16)

Obviously, (3.17) contradicts to (3.15) and then (3.17) holds, for all $t > 0$, $\forall \delta > 0$, so from (3.9),

Combining (3.18) and (3.2), we have

where

Thus, under the ETIC strategy, the QS of drive-response systems (2.2) and (2.3) with time-varying delays is achieved. When $t \to \infty$, it follows from (3.19) that the trajectory of error system (2.8) is exponentially converged to the set $\Omega$, where

The proof of QS between drive-response systems is complete. □

Remark 6. When the system degenerates into a parameter matching system, namely $\triangle\mathcal{A} = 0, \; \triangle \mathcal{B} = 0$, and $\alpha = 0$ (i.e., the effect of parameter mismatch disappears), the drive-response systems can achieve complete synchronization. In other words, Theorem 1 can be used for drive-response systems that have the same structure.

Remark 7. By using the comparison principle of impulsive systems and the formula for variable parameters, Theorem 1 gives the general results of QS of the parametric mismatch drive-response systems, and the precise synchronization error bound $\hat{\epsilon }$, and the sufficient conditions for realizing QS are derived. By selecting the appropriate positive constant $\tilde{\alpha }$ and the control gain matrix ${\mathcal{C}}, \; \mathcal{K}$, one can obtain a small error bound.

To avoid Zeno behavior, there should be a lower bound for the release interval $t_{k+1}-t_k$, and it must satisfy $\inf_{k\in N}\left\lbrace t_{k+1}-t_k\right\rbrace > 0$. Next, we will prove that the designed ETIC mechanism can eliminate the Zeno phenomenon.

Theorem 2. Considering error system (2.8) under the controller (2.4) and the conditions of Theorem 1, the impulsive instants $t_k$ can be calculated via event-triggered condition (2.10). Then, there exists a positive constant $\varkappa > 0$ such that $\inf_{k\in N}\left \{ {t_{k+1}-t_k}\right \}\geqslant \varkappa > 0$. This means that Zeno behavior in the impulsive instants for the controlled error system (2.8) is avoided.

Proof. According to Assumption 3 and (2.6), the right-upper Dini derivative of measurement error $\left\| \theta\left(t\right) \right\|$ can be calculated, for $t\in \left(t_k, t_{k+1}\right)$, and one can obtain

Then, from $\theta\left(t_k\right) = 0$, it follows that

where

Let $T_k = t_{k+1}-t_k$. Define

When the event violates triggering law (2.10), then we obtain

Based on (3.22) and (3.23), we have

For $t\in \left(t_k, t_{k+1}\right)$, we have that

If $\mathrm{X} \left (\eta\left (t_{k+1}\right)\right) = 0$, then $\eta\left (t_{k+1}\right) = \tilde{\zeta}\left (t_{k+1}\right)-\zeta\left (t_{k+1}\right) = 0$, which means $\tilde{\zeta}\left (t_{k+1}\right) = \zeta\left (t_{k+1}\right)$. However, this contradicts the fact that $\tilde{\zeta}\left (t_{k+1}\right)\neq \zeta\left (t_{k+1}\right)$. Therefore, we can conclude that

This means that for any contiguous trigger interval satisfying $\inf_{k\in N}\left \{ {t_{k+1}-t_k}\right \}\geqslant \varkappa > 0$, then the impulsive instants of error system (2.8) can avoid the Zeno behavior. The proof is complete. □

When $\mathcal{B}_1 = \mathcal{B}_2 = 0_{n\times n}$, i.e., $\triangle \mathcal{B} = 0$, the error system (2.8) degenerates into the following form:

and from Theorems 1 and 2, we have the following corollary.

Corollary 1. Suppose that the impulsive moment is generated by (2.10):

and control gain matrix $\mathcal{K}$, $\mathcal{C}$ satisfies the conditions

where $\beta_1 < 0, \; 0 < \lambda_2 < 1.$ Then system (3.26) reaches QS. The synchronization error $\eta \left (t\right)$ converges to

when $t\rightarrow \infty$, where $0 < \lambda_3\leq-\frac{\ln\lambda _2}{m_1}-\beta _1$, $m_1\geq \sup\left\lbrace t_{k+1}-t_k\right\rbrace > 0$.

4.   Numerical example

The validity of the theoretical results under the proposed ETIC strategy is verified by providing an example in this section. Considering the extensive and varied nonlinear dynamical phenomena of Chua's circuit system, such as chaos and bifurcations, we choose the following three-neuron nonlinear Chua's system with time-varying delays and parameter mismatch as the following drive system:

where

and $\delta \left(s\right) = \left(0.14, 0.1, 0.21\right) ^T$.

The corresponding response system can be described as:

where

and $\psi \left (s\right) = \left(0.6, 0.35, -0.48\right) ^T$.

Select the same parameters $c_i, \; d_i, \; \left(i = 1, ..., 4\right)$ as those in ^[38], i.e., $c_1 = 9.2156, \; c_2 = 15.9946, \; c_3 = 9.21, \; c_4 = 15.995, \; d_1 = -1.24905, \; d_2 = -0.75735, \; d_3 = -1.25, \; d_4 = -0.785, \; \rho \left (t\right) = 0.7-0.1\sin \left (t\right)$, and the nonlinear function

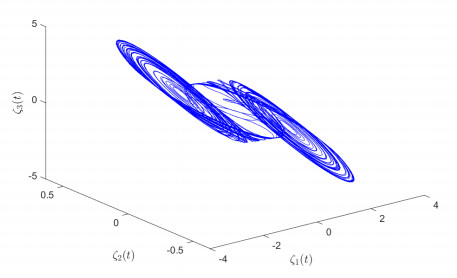
As depicted in Figure 1, it is evident that the state of drive system (4.1) is bounded, and $\left \| \zeta \left (t\right)\right \|\leq \gamma \approx 8.1430$. Correspondingly,

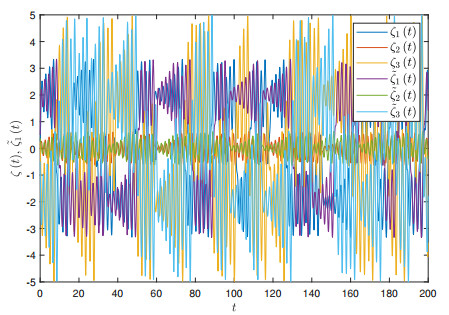
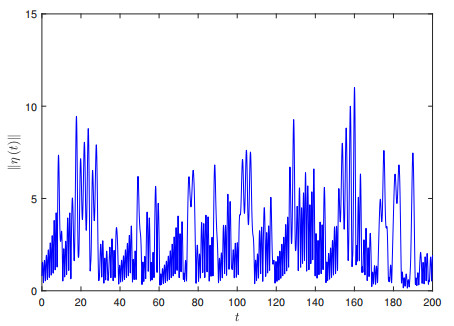
The state path of the drive-response systems without ETIC is depicted in Figure 2, and the evolution path of the error $\left\| \eta \left (t\right)\right\|$ without ETIC is shown in Figure 3.

Control gain matrix

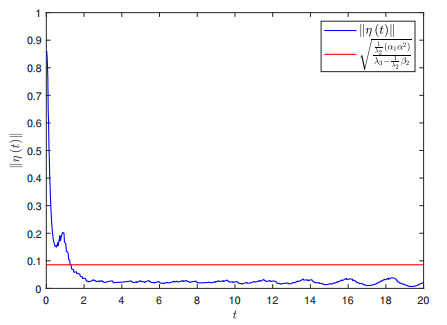
Select the appropriate parameters $\alpha_1 = 20, \; \alpha_2 = 0.023, \; \tilde{\alpha } = 3.61, \; \beta_1 = -10.427$, and Lipschitz constant $p = 1$. Then $\beta_2 = 1$ and $m_1$ is the lower bound of the trigger interval. Through the simulation program, we can obtain $m_1 = 0.06$, and accordingly, $\lambda_3\approx 27.183$. It can be verified that the conditions in Theorem 1 are true, and the theoretical synchronization error can be calculated to obtain $\left\| \eta \left (t\right)\right\| \leq 0.08571$.

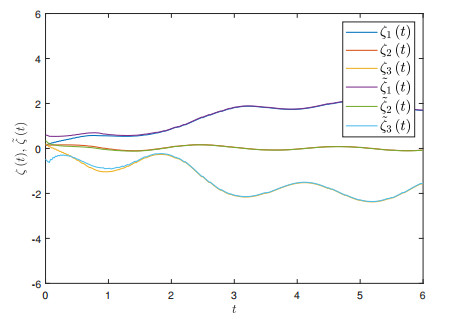
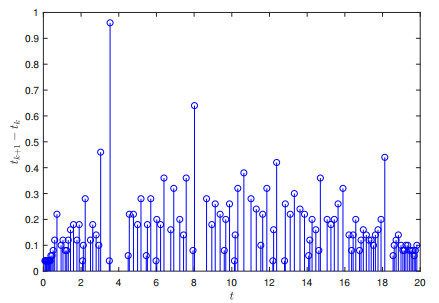
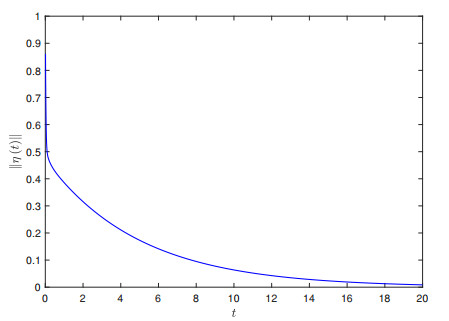
The state trajectories of drive-response system (4.1)-(4.2) with $\mathcal{U}(t)$ are shown in Figure 4, and the state evolution of $\left\| \eta \left (t\right)\right\|$ with $\mathcal{U}(t)$ is shown in Figure 5. The number of impulsive instants for the ETIC is shown in Figure 6. The simulation results show that the system error is below the theoretical value, which validates the effectiveness of our results.

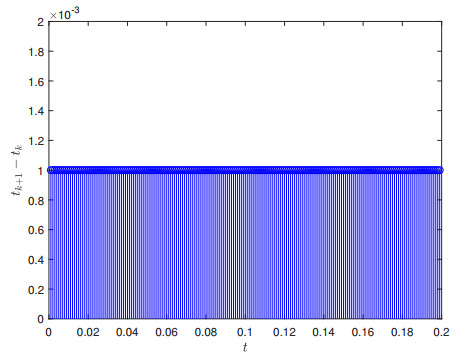
The TTIC proposed in ^[38] uses a fixed sampling interval of $\tau = 1\times 10^{-3}$, resulting in 20,000 control updates (see Figure 7). In contrast, the ETIC approach presented in this paper requires merely 118 control updates (see Figure 6). Traditional time-triggered control triggers transmissions at fixed time intervals, regardless of whether the system requires an update. On the other hand, ETIC triggers transmissions only when the system state satisfies the triggering conditions (when the error exceeds a threshold). As a result, the number of transmissions is significantly reduced, and the transmission time is more flexible. Compared to traditional TTIC, it is evident that ETIC reduces unnecessary transmissions, thereby decreasing transmission times and communication load. Additionally, while reducing transmission times, ETIC also improves system performance (faster convergence to a stable state) (see Figures 5 and 8).

5.   Conclusions

This paper investigates the QS of nonlinear drive-response systems with parameter mismatch and time-varying delays via the ETIC strategy. According to the formula for variable parameters and the comparison principle of the impulsive systems, some sufficient conditions for reaching the QS and the exact expression of the error bound are obtained. In addition we have proved that this method can avoid Zeno behavior at the impulsive instant. The event-triggered impulsive instant in the control method is determined by the state-dependent trigger law, which significantly reducing the control update frequency. It is also demonstrated that this event-triggered rule exhibits good performance.

In the future, we will consider using other control methods, such as employing the self-triggered mechanism to generate triggered sequences. This approach eliminates the need for continuous monitoring of trigger conditions and is more practical for reducing network load and communication in real-world applications.

Author contributions

Biwen Li: Supervision, writing–review, validation; Yujie Liu: Writing–original draft, formal analysis, software, methodology, writing–review and editing. Both authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that there are no conflicts of interest.