On the behavior of geodesics of left-invariant sub-Riemannian metrics on the group $\operatorname{Aff}_{0}(\mathbb{R}) \times \operatorname{Aff}_{0}(\mathbb{R})$

1.   Introduction

Recently, the study of geodesics of left-invariant sub-Riemannian metrics on Lie groups has become increasingly popular. In recent surveys by Sachkov ^[1,2], a number of sub-Riemannian problems on Lie groups integrable in elementary and elliptic functions were described: sub-Riemannian problems on the Heisenberg group, the Engel group, the Cartan group, $SE(2)$, $SH(2)$, $SO(3)$, $SU(2)$, $SL(2)$, $SO_0(2, 1)$, etc. However, in addition to cases where it is possible to find exact formulas for sub-Riemannian geodesics, there are known cases where systems of differential equations for sub-Riemannian geodesics cannot be explicitly integrated. For example, in the paper ^[3], the authors proved the nonintegrability (in the sense of Liouville) of left-invariant sub-Riemannian problems on free Carnot groups of step $4$ and greater. To prove this fact, some estimations of the separatrix splitting according to the Melnikov-Poincaré method were used. In such cases, the behavior of sub-Riemannian geodesics can only be described from a qualitative point of view.

In this paper, we consider sub-Riemannian problems on the Cartesian square of a connected two-dimensional non-commutative Lie group, where the metric is determined by some inner product on a two-dimensional generating subspace of the corresponding Lie algebra. Using the methodology of working with the Kovalevskaya exponents, we prove that the system of differential equations for covector functions is not completely integrable.

The second part of this paper is devoted to a qualitative study of the behavior of geodesics of a sub-Riemannian metric of the indicated type. The obtained results confirm the sophisticated dependence of the behavior of geodesics on the initial data. The developed qualitative research methods can be used to study similar problems related to the description of the behavior of geodesics for sub-Riemannian metrics on Lie groups.

2.   Derivation of the required system of differential equations

It is known that the connected component of the identity element in the Lie group of all invertible affine transformations of the real line is the two-dimensional Lie group ${\rm Aff}_0(\mathbb{R})$, which has the following matrix representation:

Its Lie algebra is a two-dimensional non-commutative Lie algebra ${\rm aff}_0(\mathbb{R})$.

The four-dimensional Lie algebra $\mathfrak{g} = {\rm aff}_0(\mathbb{R})\oplus{\rm aff}_0(\mathbb{R})$ has a basis $E = (E_1, E_2, E_3, E_4)$ such that

and the remaining Lie brackets of the basis vectors are zero. The simply connected Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$ is the only connected Lie group with algebra $\mathfrak{g}$:

Note that in ^[4], the authors considered the Lie group $G_{2, 1}\times G_{2, 1}$ which has a matrix realization (with a special product)

that is isomorphic to the Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$. In this case, the advantage of this realization is that the Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$ is parameterized by $\mathbb{R}^4$.

The Lie algebra $\mathfrak{g}$ of the Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$ has a satisfying (2.1) basis

Here, $e_{ij}$, $i, j = 1, \dots, 4$, denotes a four by four matrix, which has 1 in the $i$th row and the $j$th column while all other entries are 0.

In ^[5], the following proposition is proven.

Proposition 1. There exists a unique, up to automorphism of the Lie algebra $\mathfrak{g} = {\rm aff}_0(\mathbb{R})\oplus{\rm aff}_0(\mathbb{R})$, two-dimensional subspace $\mathfrak{p}\subset\mathfrak{g}$ generating $\mathfrak{g}$ by the operation $[\cdot, \cdot]$.

We recall the construction of the corresponding two-dimensional subspace. Let

It follows from (2.1) that

Obviously, the vectors $e_1, e_2, e_3, e_4$ are linearly independent (i.e., they form the basis of the Lie algebra $\mathfrak{g}$). Hence, the two-dimensional subspace $\mathfrak{p} = {\rm span}(e_1, e_2)$ generates $\mathfrak{g}$ by the operation $[\cdot, \cdot]$.

We define the distinguished inner product $(\cdot, \cdot)$ on $\mathfrak{p}$ with the orthonormal basis $e_1, e_2$. The pair $(\mathfrak{p}, (\cdot, \cdot))$ defines a sub-Riemannian metric $d$ on the Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$. The sub-Riemannian distance $d(g_0, g_1)$ between $g_0, g_1\in {\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$ is defined as the infimum of the lengths $\int\limits_{0}^{T}\sqrt{\left(dl_{g(t)^{-1}}(\dot{g}(t)), dl_{g(t)^{-1}}(\dot{g}(t))\right)}dt$ of piecewise smooth paths $g = g(t)$, $0\leq t\leq T$, such that $dl_{g(t)^{-1}}(\dot{g}(t))\in\mathfrak{p}$ and $g(0) = g_0$, $g(T) = g_1$; additionally, $T$ is not fixed.

Every sub-Riemannian space $(G, d)$ is locally compact and complete ^[6]. Therefore, by the Cohn-Vossen theorem, for any elements $g_0, g_1\in G$, there exists the shortest arc $g = g(t)$, $0\leq t\leq T$, in $(G, d)$, that connects them (i.e., an absolutely continuous curve in $G$ whose length in the metric space $(G, d)$ is equal to $d(g_0, g_1)$). Therefore, we can assume that $g$ is parameterized by the arclength (i.e., $T = d(g_0, g_1)$ and $d(g(t_1), g(t_2)) = t_2-t_1$ if $0\leq t_1\leq t_2\leq d(g_0, g_1)$).

To find geodesics of a sub-Riemannian space $(G, d)$, the Pontryagin maximum principle (PMP) ^[7] was proposed in papers ^[8,9]. For instance, the sub-Riemannian geodesics (on Lie groups) described in reviews ^[1,2] were obtained with its help. For a more detailed study of the indicated problems, we can suggest books ^[10,11].

We use the following theorem to find sub-Riemannian geodesics on ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$.

Theorem 1 (^[8]). Every shortest arc $g = g(t)$, $0\leq t\leq T = d(g_0, g_1)$, on a connected Lie group $G$ with a left-invariant sub-Riemannian metric $d$ defined by an inner product $(\cdot, \cdot)$ on a subspace $\mathfrak{p}\subset\mathfrak{g}$ of the Lie algebra $\mathfrak{g}$ of $G$, generating $\mathfrak{g}$, with $g(0) = g_0$, $g(T) = g_1$, is a solution of the time-optimal problem (with the indicated endpoints $g_0$ and $g_1$) for the control system

with a measurable control $u(t)$ and the compact control domain $U = \{u\in\mathfrak{p}\, |\, (u, u)\leq 1\}$.

By the PMP, for the time-optimality of a control $u(t)$ and the corresponding trajectory $g(t)$, $t\in [0, T]$, it is necessary that the existence of a nowhere-zero absolutely continuous covector function $\psi(t)\in T^{\ast}_{g(t)}G$ such that for almost all $t\in [0, T]$, the function $\mathcal{H}(g(t), \psi(t), u) = \psi(t)(dl_{g(t)}(u))$ (the Hamiltonian) attains its maximum at the point $u = u(t)$; i.e.,

and an analog of the Hamilton-Jacobi equation is fulfilled. Moreover, the function $M(t)$, $t\in [0, T]$, is constant and nonnegative (i.e., $M(t)\equiv M\geq 0$).

By an extremal, we will mean a parametrized curve $g(t)$ in $G$ with a maximally admissible connected domain $\Omega\subset\mathbb{R}$, which satisfies the PMP and conditions (2.8), $(u(t), u(t)) = 1$ with a measurable function $u(t)$ almost everywhere on the maximal subset in $\Omega$. In the case where $M = 0$ (respectively, $M > 0$), an extremal is called abnormal (respectively, normal). In the normal case, proportionally changing $\psi = \psi(t)$, $t\in\mathbb{R}$, if need be, we can assume that $M = 1$.

According to ^[12], every abnormal extremal of each sub-Riemannian space $(G, d)$ is nonstrictly abnormal, and so it is a geodesic (i.e., a locally shortest curve).

Unless otherwise stated, we will use the matrix realization (2.3) for the Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$.

In view of Proposition 5 in ^[13], each abnormal extremal of the sub-Riemannian space $({\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R}), d)$ is one of the two one-parameter subgroups

or its left shift. It follows from here, (2.4) and (2.5) that the abnormal extremal with the origin at the identity element has the following form:

It follows from Theorem 3 in ^[13] that this extremal is nonstrictly abnormal, and so it is a geodesic.

Next, we need the following result.

Theorem 2 (^[14]). Let $G$ be a connected Lie group with the identity element $e$ and Lie algebra $\mathfrak{g}$, let $(e_1, \dots, e_n)$ be a basis of $\mathfrak{g}$ such that $(e_1, \dots, e_r)$ is an orthonormal basis for the inner product $(\cdot, \cdot)$ on the subspace $\mathfrak{p}$ generating $\mathfrak{g}$ by the operation $[\cdot, \cdot]$, and let $d$ be a left-invariant sub-Riemannian metric on $G$ defined by the pair $(\mathfrak{p}, (\cdot, \cdot))$.

Then, every normal geodesic (parameterized by arclength) $g(t)$, $t\in\mathbb{R}$, of a sub-Riemannian space $(G, d)$ with $g(0) = e$ is a solution of the following system of differential equations:

where functions $\psi_i(t)$, $i = 1, \dots, n$, are absolutely continuous and satisfy the following system of differential equations:

Here, $C_{ij}^k$ are structure constants in the basis $(e_1, \dots, e_n)$ for $\mathfrak{g}$.

It follows from (2.4), (2.5), and (2.11) that

Therefore, taking (2.3) into account, the differential Eq (2.11) is written as the following system of differential equations:

with the initial data

Due to (2.6) and (2.7), the system (2.12) has the following form:

Let us set arbitrary initial data for this system:

Note that the equality $\varphi_1^2+\varphi_2^2 = 1$ is easily obtained from the condition $|u(0)| = 1$ (see (2.11)).

3.   Non-integrability of the covector system

From the first two Eq (2.15) and the initial conditions (2.16), it follows that

Therefore, for some differentiable function $\theta(t)$, the following equalities are satisfied:

at the same time $\psi_3(t) = \theta'(t)$. Indeed, it suffices to write out the following equations:

If $\theta_0: = \theta(0)$, then $\varphi_1 = \cos (\theta_0)$ and $\varphi_2 = \sin (\theta_0)$.

Therefore, the third and fourth equations of system (2.15) can be written as follows:

It is obvious that for the complete integrability of system (2.15), it is sufficient to determine the function $t \mapsto \theta(t)$.

Suppose that $\theta(t)\not\equiv\frac{\pi}{2}+\pi n$, $n\in\mathbb{Z}$. Let us express $\psi_4$ from the first equation in (3.1):

Let us differentiate both parts of the resulting equality and substitute it into the second equation of (3.1):

We obtain the following differential equation of the third order:

It is clear that $\theta(t)\equiv \theta_0$ is a partial solution of this equation. Since Eq (3.2) does not explicitly contain an independent variable $t$, we can lower its order by substituting $\theta'(t) = y(\theta)$, $\theta''(t) = y'(\theta)y(\theta)$, and $\theta'''(t) = y''(\theta)y^2(\theta)+y'^2(\theta)y(\theta)$. Then, we get that either $y(\theta)\equiv 0$ (i.e., $\theta(t)\equiv \theta_0$), or

Note that (3.3) is a second order differential equation of the following form:

Lie ^[15] proved that the set of equations of the following form (3.4) is closed with respect to nondegenerate point transformations of the general form:

This means that for any equation of the form (3.4), the transformed equation

also has the form (3.4). In this case, we say that Eqs (3.4) and (3.5) are equivalent with respect to the point change of variables.

This fact allows us to apply geometric methods to study equations of the form (3.4) (see ^{[16,17,18,19,20]}). From the coefficients of Eq (3.4) (i.e., the functions $P(\theta, y)$, $Q(\theta, y)$, $R(\theta, y)$, $S(\theta, y)$ and their derivatives), we can construct the Cartan differential invariants, associated with the solution.

Proposition 2. The differential Eq (3.2) cannot be reduced to an equation of the form $y'' = f(\theta, y)$ by any nondegenerate point transformation.

Proof. By ^[21], we use the notation $Z_{i, j} = \frac{\partial^{i+j}Z}{\partial \theta^{i}\partial y^{j}}$ for the second order derivatives of the function $Z$. Let

Let us consider the pseudo-invariant $F$ of weight $5$ (see details in ^[21]), discovered by J. Liouville, which has the following form:

where

As stated in ^[21], $F = 0$ for Eq (3.4) if and only if $F = 0$ for Eq (3.5), which is equivalent to (3.4) (with respect to some nondegenerate point transformation). It is easy to verify that the equality $F = 0$ is satisfied for any equation of the form $y'' = f(\theta, y)$. On the other hand, we have $F\neq 0$ for Eq (3.2). Indeed, by direct calculations, we can verify that we obtain the following relation for $F$ in the case of Eq (3.2):

The resulting formula completes the proof of Proposition 2. □

In addition, the following proposition holds.

Proposition 3. The differential Eq (3.3) has no first integral of the form $A(\theta, y)\cdot {y}'+B(\theta, y)$.

Proof. Taking (3.3) into account and the notation of paper ^[22], we find

Let us define the functions $S_1(\theta, y)$, $S_2(\theta, y)$ by the formulas (3.3) in ^[22]:

It is not difficult to see that

Since $S_1(\theta, y)\not\equiv 0$, we calculate the functions $S_3(\theta, y)$, $S_4(\theta, y)$ by formulas (3.4) and (3.6) in ^[22]:

We obtain the following:

Since $S_1(\theta, y)\not\equiv 0$ and $S_4(\theta, y)\not\equiv 0$, then, by Theorem 2 (item 2) in ^[22], Eq (3.3) has no first integral of the form $A(\theta, y)\cdot{y}'+B(\theta, y)$. □

Additionally, we should mention paper ^[23], in which the authors discussed the connection between the integrability of sub-Riemannian structures of rank two on $6$, $7$, and $8$-dimensional Carnot groups with the number of symmetries of these structures by means of special methods and computational techniques. Unfortunately, these methods turned out to be ineffective for the sub-Riemannian problems on the Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$ that we considered.

Note that the system (2.15) has homogeneous quadratic right parts; it means that the equality $f_i(\alpha\psi_1, \dots, \alpha\psi_4) = \alpha^2 f_i(\psi_1, \dots, \psi_4)$ holds for the right part $f_i(\psi_1, \dots, \psi_4)$, $i = 1, \dots, 4$, of $i$th equation of system (2.15) and any $\alpha > 0$.

Remark 1. The importance of studying such systems was already noted by S. V. Kovalevskaya. In a letter to G. Mittag-Leffler ^[24], she briefly outlined her research for a system of three equations with homogeneous quadratic right-hand sides and raised the question of studying such systems with an arbitrary number of equations. Kovalevskaya noted the great difficulties that arise in solving such a general problem. Later, in his paper, Lyapunov ^[25] developed and refined Kovalevskaya's method, which she first applied to the study of the Euler-Poisson equations, which describe the motion of a heavy rigid body around a fixed point. This made it possible to solve a more general problem of the uniqueness of the general solution as a function of a complex variable.

Let us present the necessary definitions from ^[26].

Definition 1. A system of $n$ differential equations

is called quasi-homogeneous with quasi-homogeneity exponents $g_1, \dots, g_n$, if

for all values of $x$ and $\alpha > 0$.

In other words, all equations of system (3.6) are invariant under the substitution $x_i\to\alpha^{g_i}x_i$, $t\to t/\alpha$.

For the system with homogeneous quadratic right-hand sides (in particular, for system (2.15)) we have $g_i = 1$, $i = 1, \dots, n$. In paper ^[26], it is noted that this class includes the following: 1) the Euler-Poincare equations describing geodesics on Lie groups with invariant metrics; 2) the Euler-Poisson equations describing the rotation of a heavy rigid body about a fixed point; and 3) the equations of Kirchoff's problem on the motion of a rigid body in an unbounded volume of an ideal liquid.

The quasi-homogeneous system (3.6) has a particular solution of the form $x_i(t) = c_it^{-g_i}$, $i = 1, \dots, n$, where (complex in general case) numbers $c_i$ satisfy the following system of algebraic equations:

Every nonzero solution of system (3.7) is called a balance of system (3.6) and is denoted by $c = (c_1, \dots, c_n)$.

For each balance $c$ of system (3.6), we can compute the Kovalevskaya matrix $K = (K_{ij})$:

where $\delta_{ij}$ is the Kronecker symbol.

The eigenvalues of the Kovalevskaya matrix $K = K(c)$ are called the Kovalevskaya exponents (of system (3.6)) for a given balance $c$. It was is proven in ^[27] that for every balance $c$, one of the Kovalevskaya exponents is equal to $-1$.

For system (2.15), the system of algebraic Eq (3.7) takes the following form:

Solving it, we find the balances of system (2.15):

For a given balance $c = (c_1, c_2, c_3, c_4)$, the Kovalevskaya matrix of system (2.15) has the following form:

It is easy to see that the Kovalevskaya exponents for system (2.15) (i.e., the eigenvalues of the matrix $K(c)$) are respectively equal to the following:

$-1, 1, 2, -i\quad$ for the balance $(i, 1, i, 0)$;

$-1, 1, 2, i\quad$ for the balance $(-i, 1, -i, 0)$;

$-1, 1, 2, \frac{1+i}{2}\quad$ for the balance $\left(\frac{1+i}{2}, \frac{1-i}{2}, i, -i\right)$;

$-1, 1, 2, \frac{1-i}{2}\quad$ for the balance $\left(\frac{1-i}{2}, \frac{1+i}{2}, -i, i\right)$.

We will say that the (not necessarily quasi-homogeneous) system (3.6) of $n$ differential equations is completely integrable, if it has $n-1$ functionally independent first integrals (i.e., non-constant differentiable functions constant on any solution of system (3.6)). It follows from the first two equations of (2.15) that the function $I = \psi_1^2+\psi_2^2$ is a first integral of system (2.15).

It turned out that the Kovalevskaya exponents have a direct connection with first integrals of quasi-homogeneous systems of differential equations. Apparently, Yoshida ^[27,28] was the first to notice this fact. He showed that if a quasi-homogeneous system (3.6) has $n-1$ functionally independent algebraic first integrals, then all Kovalevskaya exponents are rational numbers for each balance. Furthermore, H. Yoshida proved that if a (quasi-)homogeneous polynomial $I$ is a first integral of system (3.6), then $I(c) = 0$ for every balance $c$ of system (3.6); moreover, if $\nabla I(c)\neq 0$, then the degree of the polynomial $I$ is one of the Kovalevskaya exponents.

Later, Goriely ^[29] proved that the number of independent algebraic first integrals does not exceed the dimension of the vector space spanned by the Kovalevskaya exponents over the integers. Additionally, let us note papers ^{[30,31,32,33,34]}, which are dedicated to the Kovalevskaya exponents.

We will need the following theorem, which was proven in ^[34].

Theorem 3 (^[34]). Assume that a quasi-homogeneous system is completely integrable with meromorphic first integrals. Then, for any balance $c$,

1) the Kovalevskaya exponents are all rational numbers;

2) the size of Jordan block of the Kovalevskaya matrix with the corresponding eigenvalue $\rho\neq -1$ is one;

3) the size of Jordan block of the Kovalevskaya matrix with the corresponding eigenvalue $\rho = -1$ is one or two.

Using the above reasoning, we obtain an important result for us.

Theorem 4. The system of differential Eq (2.15) is not completely integrable with meromorphic first integrals.

Proof. According to item 1) of Theorem 3, if the system of differential Eq (2.15) is completely integrable with meromorphic first integrals, then all Kovalevskaya exponents for any balance $c$ must be rational numbers. Additionally, since one of the Kovalevskaya exponents is not (even) a real number for each balance of this system, system (2.15) is not completely integrable with meromorphic first integrals. □

Now, we extend the result of Theorem 4 to all left-invariant sub-Riemannian metrics on $\operatorname{Aff}_{0}(\mathbb{R}) \times \operatorname{Aff}_{0}(\mathbb{R})$, generated by some inner products on the subspace $\mathfrak{p} = {\rm span}(e_1, e_2)$.

The following simply provable lemma holds.

Lemma 1. Let $\langle \cdot, \cdot \rangle$ be an arbitrary inner product on $\mathfrak{p}$. Then, there exist $\alpha, \beta, \gamma \in \mathbb{R}$, $\gamma^2 \neq \alpha \beta$, and $\gamma > 0$ such that the basis $\varepsilon_1 = \gamma e_1+\alpha e_2$, $\varepsilon_2 = \beta e_1+ \gamma e_2$ is orthonormal for $\langle \cdot, \cdot \rangle$.

Proof. We choose an orthonormal basis $e_1', e_2'$ for $\langle \cdot, \cdot \rangle$ from the considerations that $e_1' = a\cdot e_1$ for a suitable $a > 0$, and $e_2'$ is orthogonal to it; therefore, $e_2' = b\cdot e_1+ c\cdot e_2$, where $b, c \in \mathbb{R}$ and $c \neq 0$. Furthermore, for any $\eta\in \mathbb{R}$, the vectors

also form an orthonormal basis for $\langle \cdot, \cdot \rangle$. If the equality $a\cdot\cos(\eta)+b\cdot\sin(\eta) = c\cdot\cos(\eta)$ holds, then we obtain the basis required in the statement of the lemma. It remains to note that there is necessarily such a real $\eta$ that the equality $(a-c)\cdot\cos(\eta)+b\cdot\sin(\eta) = 0$ is satisfied. □

Note that if $(\alpha, \beta, \gamma) = (0, 0, 1)$, then we obtain the original basis $e_1$, $e_2$, orthonormal for the inner product $(\cdot, \cdot)$. It is clear that it is sufficient to consider all inner products on $\mathfrak{p}$ up to a similarity. Therefore, we further consider that $\gamma = 1\neq \alpha \beta$.

For the vectors $\varepsilon_1 = e_1+\alpha e_2$ and $\varepsilon_2 = \beta e_1+ e_2$, it follows from (2.6) and (2.7) that

The inner product $\langle\cdot, \cdot\rangle$ on $\mathfrak{p}$ with the orthonormal basis $\varepsilon_1, \varepsilon_2$ defines some sub-Riemannian metric $\rho$ on the Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$.

By Theorem 2, each normal geodesic (parameterized by arclength) of the sub-Riemannian space $({\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R}), \rho)$ issued from the identity element is a solution of the following system of differential equations:

and absolutely continuous functions $\psi_i(t)$, $i = 1, \dots, 4$, satisfy the following system of differential equations:

Theorem 5. The system of differential Eq (3.9) is not completely integrable with meromorphic first integrals.

Proof. For (3.9), the system of algebraic Eq (3.7) takes the following form:

Solving it, we find the following balances of system (3.9):

For the balance $c = (c_1, c_2, c_3, c_4)$, the columns $K_j(c)$, $j = 1, \dots, 4$, of the Kovalevskaya matrix $K(c)$ for system (3.9) have the following form:

It is easy to see that the Kovalevskaya exponents for system (3.9) (i.e., the eigenvalues of the matrix $K(c)$) are respectively equal to the following:

$-1, 1, 2, \frac{1-\beta i}{i-\alpha}\quad$ for the balance $\left(\frac{1}{\alpha-i}, \frac{i}{i-\alpha}, i, -\alpha i\right)$;

$-1, 1, 2, \frac{1-\beta i}{1+\alpha-(1+\beta)i}\quad$ for the balance $\left(\frac{i}{1+\beta+(1+\alpha)i}, \frac{1}{1+\beta+(1+\alpha)i}, i, -(1+\alpha)i\right)$;

$-1, 1, 2, -\frac{1+\beta i}{\alpha+i}\quad$ for the balance $\left(\frac{1}{\alpha+i}, \frac{i}{\alpha+i}, -i, \alpha i\right)$;

$-1, 1, 2, \frac{1+\beta i}{1+\alpha+(1+\beta)i}\quad$ for the balance $\left(\frac{1}{1+\alpha+(1+\beta)i}, \frac{i}{1+\alpha+(1+\beta)i}, -i, (1+\alpha)i\right)$.

If the number $\frac{1-\beta i}{i-\alpha} = -\frac{\alpha+\beta+(1-\alpha \beta) i}{1+\alpha^2}$ is real, then $\alpha \beta = 1$, which is impossible. Hence, this number is not real; moreover, it is not rational. This observation and item 1) of Theorem 3 implies the result we need. □

4.   Study of the system of eight differential equations

In what follows, we will consider only the sub-Riemannian metric on the Lie group $\operatorname{Aff}_{0}(\mathbb{R}) \times \operatorname{Aff}_{0}(\mathbb{R})$ generated by the distinguished inner product $(\cdot, \cdot)$ on $\mathfrak{p}$ with an orthonormal basis $e_1, e_2$, see Section 2. Note that all the methods used below can also be applied in the case where the sub-Riemannian metric is generated by another inner product. In addition, they can also be useful in studying geodesics of sub-Riemannian metrics on other Lie groups.

In this section, we will establish some general properties of solutions of the previously obtained system of ordinary differential Eq (2.13)+(2.15) with the initial data (2.14)+(2.16).

Let us recall a well-known fact.

Lemma 2. If the equality $u'(t)+u(t)\cdot v(t) = 0$ is satisfied on some interval $(a, b) \subset \mathbb{R}$, then $u(t) = C\cdot \exp(-V(t))$, where $V$ is an arbitrary primitive of the function $v(t)$ on $(a, b)$, and $C$ is some constant. In particular, the function $u(t)$ does not change the sign on the interval $(a, b)$.

Proof. Simple calculations imply the following:

which is what we wanted. □

Theorem 6. For any solution of the ordinary deferential equation (ODE) system (2.13)+(2.15) with the initial data (2.14)+(2.16), the following relations are satisfied:

Proof. Equalities (4.1) and (4.2) follow immediately from Lemma 2, since $\psi_4(0) = \varphi_4$, $\psi_3(0)+ \psi_4(0) = \varphi_3+\varphi_4$, $x_1(0) = x_3(0) = 0$ and

Let us prove relation (4.3). It is easily verified that it is valid for $t = 0$. Therefore, it suffices to verify that the derivatives of its left and right sides are equal. Given (4.1), we have

which is what was required.

It remains to prove equality (4.4). Obviously, it is satisfied for $t = 0$. Therefore, it suffices to verify that the derivatives of its left and right sides are equal. Given (4.2), we have

which completes the proof. □

Expressing successively the values of $\psi_4$, $\psi_3$, $\psi_1$ and $\psi_2$ from the equalities of Theorem 6, we obtain the following statement.

Corollary 1. Under the conditions of Theorem 6 the following equalities are satisfied:

Corollary 1 implies the following remarkable result.

Theorem 7. For any solution of the ODE system (2.13)+(2.15) with the initial data (2.14)+(2.16) the following equality holds:

In particular, the following inequalities are satisfied:

Proof. Since $\psi_1^2(t)+\psi_2^2(t)\equiv 1$, as was indicated in the previous section, it is sufficient to use the first two equalities from the formulation of Corollary 1. □

Using Theorem 6, it is also easy to obtain an expression for the functions $x_1(t)$, $x_2(t)$, $x_3(t)$, $x_4(t)$ in terms of $\psi_i(t)$, $i = 1, 2, 3, 4$.

Corollary 2. Let the conditions of Theorem 6 be satisfied. Then, for $\varphi_4\neq 0$, the equalities

hold, and for $\varphi_3+\varphi_4\neq 0$, the following equalities hold:

Let us consider the functions $v_i(t)$ associated with the functions $x_i(t)$, $i = 1, 2, 3, 4$, as follows (here, we essentially use another realization for the Lie group ${\rm Aff}_0(\mathbb{R})\times {\rm Aff}_0(\mathbb{R})$, see the discussion at the beginning of Section 2):

Then, the system (2.13) is transformed into the following one:

and the more general system (3.8) takes the following form:

Theorem 8. The system of differential Eq (4.8)+(2.15) is not Liouville integrable in the class of meromorphic functions.

Proof. Let us suppose that there exist $4$ independent pairwise commuting in the sense of the Poisson bracket meromorphic first integrals $\Phi_i(v_1, v_2, v_3, v_4, \psi_1, \psi_2, \psi_3, \psi_4)$, $i = 1, 2, 3, 4$. Using the formulas from Corollary 2, we obtain (for $\varphi_4\neq 0$ and $\varphi_3+\varphi_4\neq 0$) the following:

Substituting these (rational) expressions of the functions $v_i(t)$, $i = 1, 2, 3, 4$, through $\psi_j(t)$, $j = 1, 2, 3, 4$, into the first integrals $\Phi_1, \Phi_2, \Phi_3, \Phi_4$, we obtain four independent first meromorphic integrals for the system of Eq (2.15), which is impossible by Theorem 4. The resulting contradiction proves the theorem. □

Remark 2. By an analogy with the proof of Theorem 8, it can be shown that the system of differential Eq (4.9)+(2.15) is not Liouville integrable in the class of meromorphic functions.

The previous arguments show that the solution of the original system of eight differential equations can be reduced to the solution of an ODE system of four equations. One of the options is obvious. It is enough to solve the system of Eq (2.15), which consists of four equations, and obtain solutions of the system (2.13), using the result of Corollary 2.

Another version of such a reduction is the following. Given that $\psi_3(t) = (\varphi_3+\varphi_4) \cdot e^{-x_3(t)}-\varphi_4 \cdot e^{-x_1(t)}$ and $\psi_4(t) = \varphi_4 \cdot e^{-x_1(t)}$ according to Corollary 1, it is sufficient for us to determine the remaining six functions from the corresponding six differential equations. In this case, a group of four equations is solved independently of the others. These equations are as follows:

where $\psi_3(t) = (\varphi_3+\varphi_4) \cdot e^{-x_3(t)}-\varphi_4 \cdot e^{-x_1(t)}$.

The functions $x_2(t)$ and $x_4(t)$ are easily found at the last stage from the equalities $x_2' = \psi_1\cdot e^{-x_1}$ and $x_4' = \psi_1\cdot e^{-x_3}$ (or from equalities (4.3) and (4.4) for $\varphi_4 \neq 0$ and $\varphi_3+ \varphi_4\neq 0$).

As was already done at the beginning of Section 3, we can define a function $\theta(t)$ such that $\psi_1(t) = \cos\theta(t)$ and $\psi_2(t) = \sin\theta(t)$. Let $\theta_0 = \theta(0)$, then $\varphi_1 = \cos\theta_0$ and $\varphi_2 = \sin\theta_0$. Without a loss of generality, we can assume that $\theta_0\in [0, 2\pi)$.

Therefore, the ODE system (4.10) is reduced to the following system of three differential equations:

where $x_1(0) = x_3(0) = 0$, $\theta(0) = \theta_0$.

If we set

then the system (4.11) takes the following form:

where $y(0) = z(0) = 0$, $\theta(0) = \theta_0$.

5.   Study of the system of Eq (4.13)

Lemma 3. If $\alpha\cdot \beta < 0$ in the system of Eq (4.13), then the inequality $\beta \cdot \theta'(t) < 0$ holds for any real number $t$. In particular, the function $\theta(t)$ strictly increases (strictly decreases) when $\beta < 0$ (respectively, $\beta > 0$).

Proof. Everything follows from the fact that $\alpha\cdot \beta < 0$ and $\beta\cdot \theta'(t) = \alpha\cdot\beta\cdot \exp(-z(t))-\beta^2 \cdot \exp(-y(t)-z(t)) < 0$. □

Remark 3. If functions $y(t)$, $z(t)$, and $\theta(t)$ satisfy the system of Eq (4.13) and $y(0) = z(0) = 0$, $\theta(0) = \theta_0$, then the functions $\tilde{y}(t) = y(-t)$, $\tilde{z}(t) = z(-t)$, $\tilde{\theta}(t) = \theta(-t)+\pi$ satisfy the system of equations $\tilde{y}\, '(t) = \cos\tilde{\theta}(t)$, $\tilde{z}\, '(t) = \sin\tilde{\theta}(t)$, $\tilde{\theta}\, '(t) = -\alpha \cdot \exp(-\tilde{z}(t))+\beta \cdot \exp(-\tilde{y}(t)-\tilde{z}(t))$, where $\tilde{y}(0) = \tilde{z}(0) = 0$, $\tilde{\theta}(0) = \theta_0+\pi$, that is, the same system of Eq (4.13) with $\alpha, \beta, \theta_0$ replaced by $-\alpha, -\beta, \theta_0+\pi$, respectively.

Theorem 9. The ODE system (4.13) with the initial data $y(0) = z(0) = 0$ and $\theta(0) = \theta_0$ has a unique solution defined on the entire real axis. In this case, all the sought functions turn out to be real analytic, and for all $t\in \mathbb{R}$, the following inequalities are satisfied:

Proof. The system of ODEs under consideration is a normal system of differential equations with a real analytic right-hand side, which is defined on the entire real axis. For such a system, the Cauchy problem is locally uniquely solvable for any initial data. Moreover, the solutions of such a system for any initial data are real analytic functions of the variable $t \in \mathbb{R}$; for example, see Theorem 1.8.1 in ^[35]. To prove that the functions $y(t)$, $z(t)$, and $\theta(t)$ are defined on the entire real axis, it suffices to prove that none of them goes to infinity in a finite time (for example, see Theorem 3.1 in ^[36]). This fact easily follows from the inequalities in the formulation of the theorem, which remain to be proven. Since $|\sin\theta(t)|\leq 1$ and $|\cos\theta(t)+\sin\theta(t)| = \sqrt{2}|\sin(\pi/4+\theta(t))|\leq \sqrt{2}$ for all $t \in \mathbb{R}$, then

Using these inequalities and the inequality $\exp(s)\leq \exp(|s|)$, we obtain the following:

Therefore,

The theorem is completely proven. □

The following lemma is of great importance for the study of the asymptotic behavior of solutions of the system of Eq (4.13).

Lemma 4. For an arbitrary solution of the system of Eq (4.13), the function

does not increase on $\mathbb{R}$ and $F(0) = 0$. Additionally, if $\alpha^2+ \beta^2 \neq 0$, then this function is strictly decreasing.

Proof. It is clear that $F(0) = 0$. Given (4.13), it is easy to verify, that

It is clear that $F'(t) = 0$ is equivalent to $\sin\theta(t) = 0$. By analyticity, either the set of zeros of $t \mapsto \sin\theta(t)$ is discrete (in which case $F(t)$ is strictly decreasing) or $\sin\theta(t)\equiv 0$. In the latter case, $\theta(t)\equiv \pi n$ for some $n \in \mathbb{N}$; therefore, $\cos\theta(t)\equiv (-1)^n$, $z(t)\equiv 0$, $y(t) = (-1)^n t$, $\theta'(t) = \alpha-\beta \cdot\exp((-1)^{n+1}t)$. Since $\theta'(t)\equiv 0$ only when $\alpha = \beta = 0$, then $\alpha^2+ \beta^2 \neq 0$ implies $\sin\theta(t)\not \equiv 0$. □

For fixed numbers $\alpha, \beta\in \mathbb{R}$, let us consider the following function:

Lemma 4 means that (for $\alpha^2+\beta^2 \neq 0$) the value of the function $\Psi$ decreases along the curve $\gamma(t) = (y(t), z(t), \theta(t))$, which is a solution to the system of differential Eq (4.13), since $\Psi(\gamma (0)) = -\sin\theta_0$ and $F(t) = \Psi(\gamma (t))+\sin\theta_0 = \Psi(y(t), z(t), \theta(t))+\sin\theta_0$.

In other words, the vector $\gamma'(t)$ (formed from the right-hand sides of the system of Eq (4.13)) forms an obtuse angle with the gradient vector $\nabla \Psi$ at the point $\gamma(t)$. Therefore, knowledge of the important properties of the level surfaces

of the function $\Psi$ helps to understand the behavior of solutions of system (4.13).

Note that $\Psi(y, z, \pi-\theta) = \Psi(y, z, \theta) = \Psi(y, z, \theta+2\pi)$; therefore, any level surface $S(C)$ is symmetric with respect to the plane $\theta = \pi/2$ and $\theta$ can be assumed to lie on the circle $\mathbb{R}/(2\pi \cdot \mathbb{Z})$. Thus, it is sufficient to study the properties of $S(C)$ for $\theta \in [-\pi/2, \pi/2]$. This part of the surface is given by the following formula:

where $\bigl|\alpha\cdot y+\beta \cdot (e^{-y}-1)-C\bigl|\leq e^{z}$.

If we fix $y$ in (5.1) and (5.2), then we immediately obtain that the image of the function $(y, z, \theta) \mapsto \Psi(y, z, \theta)$ is $\mathbb{R}$, given that the images of the functions $z \mapsto e^{z}$ and $\theta \mapsto\sin\theta$ are $(0, \infty)$ and $[-1, 1]$, respectively. Therefore, the level surface $S(C)$ is a non-empty set for each $C\in \mathbb{R}$.

Moreover,

Therefore, $\nabla \Psi$ vanishes nowhere and each level surface $S(C)$ is a smooth two-dimensional surface in three-dimensional space. Moreover, any two such surfaces are diffeomorphic to each other (one is mapped to the other by the gradient flow $\nabla \Psi$). Therefore, each level surface $S(C)$ is diffeomorphic to the Euclidean plane.

In addition to Lemma 4, we prove the following proposition.

Proposition 4. For an arbitrary solution of the system of Eq (4.13) with $\alpha^2+ \beta^2 \neq 0$, the function

is strictly decreasing. In this case, $F(t) \to -\infty$ for $t \to \infty$ and $F(t) \to \infty$ for $t \to -\infty$. Moreover, the integrals $\int\limits_{-\infty}^0 e^{\, z(t)}\cdot \bigl(z'(t)\bigr)^2 dt$ and $\int\limits_{0}^{\infty}e^{\, z(t)}\cdot \bigl(z'(t)\bigr)^2 dt$ diverge.

Proof. The first assertion is proven in Lemma 4. This means that the value of the function $\Psi$ decreases along the curve $\gamma(t) = (y(t), z(t), \theta(t))$, see (5.1). However, as shown above, the level surface $S(C)$ is a nonempty set for each $C\in \mathbb{R}$, and $\nabla \Psi$ vanishes nowhere. Therefore, the curve $\gamma(t)$ must transversally pass through each level surface $S(C)$, and the function $t \mapsto F(t)$ takes all real values, being strictly decreasing. The second assertion immediately follows from this.

Finally, since $F'(t) = -e^{\, z(t)}\bigl(\sin\theta(t)\bigr)^2$ (see the proof of Lemma 4), then

that is, the corresponding integrals diverge. □

We can consider another parametrization of the surface $S(C)$. Let us consider $SZ: = \left\{(y, z, \theta)\in \mathbb{R}^3\, |\, \sin\theta = 0 \right\}$ ($\sin\theta = 0$ is equivalent to $\theta = \pi n$ for some $n \in \mathbb{Z}$); then, for any $C\in \mathbb{R}$, we obtain the following:

where $(\alpha\cdot y+\beta \cdot (e^{-y}-1)-C)\cdot \sin\theta > 0$.

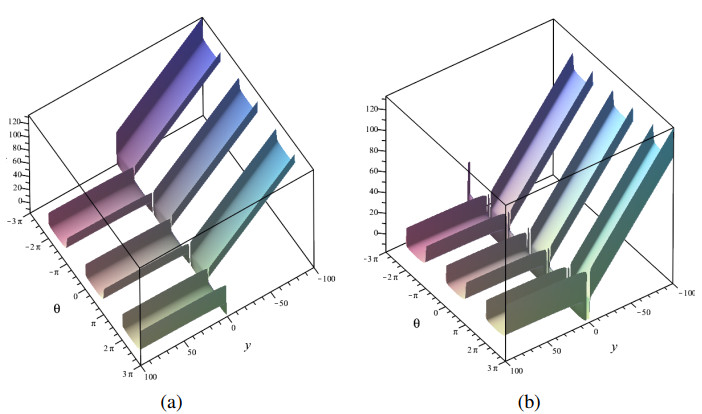
It is clear that $S(C) = (S(C)\cap SZ) \bigcup (S(C)\setminus SZ)$, and the surface $S(C)$ is not bounded, since its orthogonal projection onto the second coordinate line (the axis of the variable $z$) is surjective. Indeed, the set $S(C)\cap SZ$ is not empty and is the union of lines parallel to the second coordinate line. The formulas (5.5) and (5.6) are useful to obtain a good visualization of the level surfaces $S(C)$ for different $C\in \mathbb{R}$. It should be noted that, in the neighborhoods of points from $S(C)\cap SZ$, it is very difficult to obtain any informative image of points from $S(C)$.

Figures 1 (a), (b) show the surface $S(C)$ for $\alpha = 1$, $\beta = -2$, $C = 1$ and $\alpha = 1$, $\beta = 2$, $C = 1$, respectively.

Note that here and below the images of the corresponding surfaces and curves are obtained using Maple (see, for example, ^[37]).

For fixed numbers $\alpha, \beta \in \mathbb{R}$, we consider the following function:

Lemma 5. For the above-defined function $\Phi: \mathbb{R}\rightarrow \mathbb{R}$, the following assertions are true:

1) For $\alpha > 0$ and $\beta < 0$, the function $\Phi$ strictly increases on $\mathbb{R}$ and takes all values from $\mathbb{R}$;

2) For $\alpha < 0$ and $\beta > 0$, the function $\Phi$ strictly decreases on $\mathbb{R}$ and takes all values from $\mathbb{R}$;

3) For $\alpha > 0$ and $\beta > 0$, the function $\Phi$ reaches its lowest value at the point $s_0 = -\ln \frac{\alpha}{\beta}$, while $\Phi(s_0) = -\alpha \cdot \ln \frac{\alpha}{\beta}+\alpha -\beta$, and $\lim\limits_{s\to \pm \infty} \Phi(s) = \infty$;

4) For $\alpha < 0$ and $\beta < 0$, the function $\Phi$ reaches its greatest value at the point $s_0 = -\ln \frac{\alpha}{\beta}$, while $\Phi(s_0) = -\alpha \cdot \ln \frac{\alpha}{\beta}+\alpha -\beta$, and $\lim\limits_{s\to \pm \infty} \Phi(s) = -\infty$.

Proof. It is clear that $\Phi'(s) = \alpha - \beta \cdot \exp(-s)$ and the only critical point of the function $\Phi$ is the point $s_0 = -\ln \frac{\alpha}{\beta}$ (in this case, the inequality $\alpha\cdot \beta > 0$ must be satisfied). From here, the assertions of the lemma about the case $\alpha \cdot \beta < 0$ immediately follow. It is easy to verify that $s_0$ is the point of absolute minimum (maximum) of the function $\Phi$ for $\alpha > 0$ and $\beta > 0$ (respectively, for $\alpha < 0$ and $\beta < 0$). □

Lemma 6. Let $(y, z, \theta) \in S(C)$, then $\Phi(y)-e^{z}\cdot \sin\theta = \Psi(y, z, \theta) = C$. In this case, the inequalities $e^{z}+\Phi(y)\geq C$ and $e^{z}-\Phi(y)\geq -C$ are satisfied.

Proof. The first assertion follows from the definitions of the functions $\Psi$ and $\Phi$ (see (5.1) and (5.7)). Furthermore, since $|\sin\theta|\leq 1$, we obtain $e^{z}\geq |\Phi(y)-C|$, which means that the inequalities $e^{z}\geq C-\Phi(y)$ and $e^{z}\geq \Phi(y)-C$ are simultaneously satisfied. □

Proposition 5. For an arbitrary solution $(y(t), z(t), \theta(t))$ of the system of Eq (4.13), we have the asymptotics $C(t)\to \infty$ as $t \to -\infty$ and $C(t)\to -\infty$ as $t \to \infty$, where $C(t): = \Psi(y(t), z(t), \theta(t))$. In particular, $e^{\, z(t)}+\Phi(y(t)) \rightarrow \infty$ as $t \to -\infty$ and $e^{\, z(t)}-\Phi(y(t))\rightarrow \infty$ as $t \to \infty$.

Proof. Since $(y(t), z(t), \theta(t))\in S\bigl(C(t)\bigr)$ and

by the definition of the corresponding quantities, and $F(t) \to -\infty$ as $t \to \infty$ and $F(t) \to \infty$ as $t \to -\infty$ by Proposition 4; then $C(t) \to -\infty$ as $t \to \infty$ and $C(t) \to \infty$ as $t \to -\infty$. From Lemma 6, we obtain $e^{\, z(t)}+\Phi(y(t))\geq C(t)$ and $e^{\, z(t)}-\Phi(y(t))\geq -C(t)$.

For $t \to -\infty$, we have $e^{\, z(t)}+\Phi(y(t))\to \infty$, since even $C(t) \to \infty$. For $t \to \infty$, we have $e^{\, z(t)}-\Phi(y(t))$, since even $-C(t)\to \infty$. The proposition is proven. □

Remark 4. Proposition 5 can be used to study the asymptotics of the solution of the system of Eq (4.13). For example, if $\alpha > 0$ and $\beta < 0$, then the function $\Phi$ strictly increases on $\mathbb{R}$ according to Lemma 5.

Now, if $\liminf\limits_{t \to \infty} z(t) < \infty$, then $\liminf\limits_{t \to \infty} e^{\, z(t)} < \infty$ and, since $e^{\, z(t)}-\Phi(y(t))\to \infty$ as $t \to \infty$, we obtain $\limsup\limits_{t \to \infty} (-\Phi(y(t))) = \infty$ or $\liminf\limits_{t \to \infty} \Phi(y(t)) = -\infty$ and $\liminf\limits_{t \to \infty} y(t) = -\infty$ (the function $\Phi$ is strictly increasing).

Similarly, if $\liminf\limits_{t \to -\infty} z(t) < \infty$, then $\liminf\limits_{t \to -\infty} e^{\, z(t)} < \infty$ and, since $e^{\, z(t)}+\Phi(y(t))\to \infty$ as $t \to -\infty$, we obtain $\limsup\limits_{t \to -\infty} (\Phi(y(t))) = \infty$ or $\limsup\limits_{t \to -\infty} y(t) = \infty$.

The following corollary is useful to study the case when $\alpha\cdot \beta > 0$.

Corollary 3. Let $(y(t), z(t), \theta(t))$ be an arbitrary solution of the system of Eq (4.13) for $\alpha > 0$ and $\beta > 0$ ($\alpha < 0$ and $\beta < 0$). Then, $z(t) \to \infty$ for $t \to \infty$ (respectively, for $t \to -\infty$).

Proof. Recall that $e^{\, z(t)}+\Phi(y(t)) \to \infty$ as $t \to -\infty$ and $e^{\, z(t)}-\Phi(y(t))\to \infty$ as $t \to \infty$ by Proposition 5.

For $\alpha > 0$ and $\beta > 0$, the function $s \mapsto \Phi(s)$ attains its smallest value at the point $s_0 = -\ln \frac{\alpha}{\beta}$, while $\Phi(s_0) = -\alpha \cdot \ln \frac{\alpha}{\beta}+\alpha -\beta$, see Lemma 5. Therefore, $-\Phi(y(t))\leq -\Phi(s_0)$ for all $t$. Since $e^{\, z(t)}-\Phi(y(t))\to \infty$ as $t \to \infty$, then $e^{\, z(t)} \to \infty$ or, equivalently, $z(t) \to \infty$ as $t \to \infty$.

For $\alpha < 0$ and $\beta < 0$, the function $s \mapsto \Phi(s)$ attains its greatest value at the point $s_0 = -\ln \frac{\alpha}{\beta}$, while $\Phi(s_0) = -\alpha \cdot \ln \frac{\alpha}{\beta}+\alpha -\beta$. Therefore, $\Phi(y(t))\leq \Phi(s_0)$ for all $t$. Since $e^{\, z(t)}+\Phi(y(t))\to \infty$ as $t \to -\infty$, then $e^{\, z(t)} \to \infty$ or, equivalently, $z(t) \to \infty$ as $t \to -\infty$. □

Theorem 10. In the notation of Lemma 5, let $\alpha > 0$, $\beta > 0$, and $\theta_0 = \theta(0) \in (0, \pi)$ be such that

Then, for the corresponding solution of the system of Eq (4.13), the inequality

holds for all $t > 0$. In addition, the following assertions are true:

1) $\theta(t) \in (0, \pi)$ for all $t \in (0, \infty)$;

2) $z'(t) = \sin\theta(t) > 0$ for all $t \in (0, \infty)$; therefore, $z(t)$ strictly increases on the positive semi-axis;

3) $z(t) \geq \ln (1+\kappa t)$ for all $t \in (0, \infty)$, in particular, $z(t) \to \infty$ for $t \to \infty$;

4) $\cos\theta(t)-\cos\theta_0 > -\alpha\cdot \bigl(1-e^{-z(t)}\bigr)$ for $t\in (0, \infty)$;

5) the function $t \mapsto \ln\Bigl(\tan \bigl(\theta(t)/2\bigr) \Bigr)-\eta \cdot t$, where $\eta = \alpha/\kappa$, strictly decreases on $(0, \infty)$.

Proof. Note that under the conditions of the theorem being proven, the equality

holds, where $\Phi(s) = \alpha \cdot s+ \beta \cdot \bigl(e^{-s}-1\bigr)$ and $F(t) = \alpha\cdot y(t)+ \beta \cdot \left(e^{-y(t)}-1\right)-e^{z(t)}\cdot \sin\theta(t)+\sin\theta_0$ (see Lemma 4).

By Lemma 5, we have the inequality $\Phi(y(t))\geq \Phi(s_0)$. Since $\Phi(s_0) \in (-1, 0]$ by the conditions of the theorem, then $\Phi(y(t))+\sin\theta_0 \geq \Phi(s_0)+\sin\theta_0 > 0$. By Lemma 4, $F(t) < 0$ for all positive $t$. Therefore,

for all $t > 0$.

From the inequality $e^{z(t)} \cdot \sin\theta(t) > 0$, we obtain $\sin\theta(t) > 0$ for all positive $t$. Since the function $\sin\theta(t)$ does not vanish for $t\in (0, \infty)$ and $\theta(0) \in (0, \pi)$, then $\theta(t) \in (0, \pi)$ for all $t \in (0, \infty)$, which proves 1).

The proof of assertion 2) follows from the previous assertion and the fact that $z'(t) = \sin\theta(t)$. Additionally, the last equality implies the inequality $e^{z(t)}z'(t) > \kappa$, thereby integrating which we obtain $e^{z(t)}-1 = e^{z(t)}-e^{z(0)} > \kappa\cdot t$ for all $t \in (0, \infty)$, which proves assertion 3).

Furthermore, since $\theta'(t) = \alpha\cdot e^{-z(t)}- \beta \cdot e^{-y(t)-z(t)} < \alpha \cdot e^{-z(t)}$ and $\sin\theta(t) = z'(t)$, then $-\sin\theta(t)\, \, \theta'(t) > -\alpha \cdot e^{-z(t)}z'(t)$, from which, by integration, we obtain the following:

Thus, we have proved assertion 4).

Finally, the derivative of the function $t \mapsto \ln\Bigl(\tan \bigl(\theta(t)/2\bigr) \Bigr)-\eta \cdot t$ is equal to $\frac{\theta'(t)}{\sin\theta(t)}-\eta$. Since (as is easy to follow from the above calculations)

and $\sin\theta(t) > 0$ for $t \in (0, \infty)$, then this derivative is negative for positive values of $t$, which proves assertion 5). The theorem is completely proven. □

Lemma 7. The function $H(\gamma): = \gamma-(1+\gamma)\ln (1+\gamma)$ is strictly increasing for $\gamma \in (-1, 0]$ and strictly decreasing for $\gamma \in [0, \infty)$. Moreover, $H(0) = 0$ and $\lim\limits_{\gamma\to -1+0}H(\gamma) = -1 = H(e-1)$, where $e = \lim\limits_{n\to \infty} \left(1+\frac{1}{n}\right)^n$. In particular, $H(\alpha-1) \in(-1, 0]$ for $\alpha \in (0, e)$.

Proof. It is clear that $H'(\gamma) = -\ln (1+\gamma)$, which immediately implies the first assertion of the lemma. The second assertion can be easily obtained using standard calculations, since $\ln(1) = 0$, $\ln(e) = 1$ and

by L'Hopital's rule. □

Remark 5. From Lemma 7, it follows that

for $\beta \in (0, 1]$ and $\alpha/\beta \in (0, e)$ (recall that $s_0 = - \ln \frac{\alpha}{\beta} )$. Therefore, in particular, for $\beta = 1$ and $\alpha \in (0, e)$, we can choose $\theta_0 = \theta(0) \in (0, \pi)$, thus satisfying the conditions of Theorem 10.

Theorem 11. In the notation of Lemma 5, let $\alpha > 0$, $\beta > 0$, $\Phi(s_0) = \alpha-\beta-\alpha \cdot \ln \frac{\alpha}{\beta}\in(-1, 0]$; the solution of the system of Eq (4.13) is such that

Then, $y(t)+ z(t)\to \infty$ and $z(t) \to \infty$ as $t \to \infty$, and the function $z(t)$ strictly increases on the positive semi-axis. As a consequence, $\theta'(t) \to 0$ as $t \to \infty$.

Proof. The existence of the required properties of the function $z(t)$ is proven in Theorem 10. Therefore, it remains for us to prove that $\theta'(t) \to 0$ and $y(t)+ z(t) \to \infty$ as $t \to \infty$ under the conditions of the theorem.

Suppose that the inequality $M^{-}\neq M^{+}$ holds for the solution of system (4.13) under consideration, where $M^{-} = \liminf\limits_{t \to \infty} \theta'(t)$ and $M^{+} = \limsup\limits_{t \to \infty} \theta'(t)$. Then, there exists a real sequence $\{\tau_n\}_{n \in \mathbb{N}}$ such that $\theta''(\tau_n) = 0$, $\tau_n \to \infty$ and $\theta'(\tau_n)\to L \in \{M^{-}, M^{+}\}$ as $n \to \infty$, and $L\neq 0$. Indeed, let $L$ be a nonzero element of the set $\{M^{-}, M^{+}\}$. Since $M^{-}\neq M^{+}$, there exists a sequence of local extrema (local maxima for $L = M^{+}$ and local minima for $L = M^{-}$) $\{\tau_n\}_{n \in \mathbb{N}}$ for the function $\theta'(t)$ such that $\theta'(\tau_n) \to L$ for $n\to \infty$. It is clear that $\theta''(\tau_n) = 0$ for all $n\in\mathbb{N}$.

Since $\theta'(t) = \alpha\cdot e^{-z(t)}-\beta \cdot e^{-y(t)-z(t)}$ and $e^{-z(t)} \to 0$ as $t \to \infty$, we obtain $\beta \cdot e^{-y(\tau_n)-z(\tau_n)}\to -L\neq 0$ as $n\to \infty$. Moreover, differentiating the third equation of system (4.13), we obtain

since $y'(t) = \cos\theta(t)$ and $z'(t) = \sin\theta(t)$.

Since $e^{-z(\tau_n)}\to 0$ and $\beta \cdot e^{-y(\tau_n)-z(\tau_n)}\to -L\neq 0$ as $n\to \infty$, we obtain the asymptotics $\cos(\theta(\tau_n))+\sin(\theta(\tau_n)) \to 0$ as $n \to \infty$. The condition $\theta(t) \in (0, \pi)$ for a positive $t$ (see Theorem 10) is equivalent to $\cos\theta(\tau_n) \to -1/\sqrt{2}$ (or $\theta(\tau_n) \to 3\pi/4$) as $n \to \infty$.

By assertion 4) of Theorem 10, we have the following inequality:

for $t\in (0, \infty)$. Since $\cos\theta_0-\alpha > -1/\sqrt{2}$ by the conditions of the theorem and $e^{-z(t)} \to 0$ as $t \to \infty$, there exists $\varepsilon > 0$ such that $\cos\theta(t) > -1/\sqrt{2}+\varepsilon$ for sufficiently large $t$. This inequality contradicts the asymptotics $\cos\theta(\tau_n) \to -1/\sqrt{2}$ as $n \to \infty$. The resulting contradiction proves that $M: = M^{-} = M^{+}$ under the conditions of the theorem (i.e. the function $\theta'(t)$ has a certain (possibly infinite) limit $M$ as $t \to \infty$).

In our case, recall that $\theta'(t) = \alpha\cdot e^{-z(t)}-\beta \cdot e^{-y(t)-z(t)}$. Since $e^{-z(t)} \to 0$ as $t \to \infty$, then $M \leq 0$. If we assume that $M < 0$, then $\theta(t)\to -\infty$ as $t \to \infty$. It is clear that the asymptotics $\theta(t)\to -\infty$ as $t \to \infty$ contradicts the fact that $\theta(t) \in (0, \pi)$. Thus, $M = 0$, where we obtain that $y(t)+z(t) \to \infty$ as $t \to \infty$. The theorem is completely proven. □

Let us choose $\alpha = 1$, $\beta = 2$, and $\theta_0 = \pi/4$. Then, it is easy to see that all the conditions of Theorem 11 are satisfied. Figure 2 shows the graphs of the functions $x_i(t)$, $i = 1, \dots, 4$, which are solutions of system (2.13) and the graph of the function $\theta(t)$.

Remark 6. Taking Remark 3 into account, it is easy to obtain analogues of Theorems 10 and 11 for $\alpha < 0$ and $\beta < 0$, which deal with the asymptotics of the corresponding functions as $t \rightarrow -\infty$.

6.   Relationship with plane curve geometry

Note that the system of differential Eq (4.13) defines the natural equation (the Frenet equation) of a plane curve $\gamma(t): = (y(t), z(t))\in \mathbb{R}^2$ with an arc length $t$ and a curvature function $k(t) = \exp(-z(t))\bigl(\alpha -\beta \cdot \exp(-y(t)\bigr)$, for example, see ^[38,39,40].

It should be noted that the expression for the curvature $k(t)$ essentially depends on the choice of the initial value $\theta_0$, since the values of the functions $y(t)$ and $z(t)$ depend on this choice.

Definition 2. If a curve $\gamma(t)$ in $\mathbb{R}^2$ is parameterized by the arclength $t$ with the curvature function $k(t)$, then the quantity $R(t_1, t_2): = \int\limits_{t_1}^{t_2} k(t) dt$ is called its turning angle on the interval $[t_1, t_2]$. The turning angle of a curve on its domain of definition is called the integral curvature.

In the case of the system of differential Eq (4.13), we have the following:

In a number of cases, using the limit passage, it is possible to correctly determine the turning angle of the curve on the rays $(-\infty, t_0]$, $[t_0, \infty)$ or even on the entire curve (on the line $(-\infty, \infty)$).

Let us recall several properties of the curvature of plane curves.

If the arcs of the plane curves $\gamma_1(t)$ and $\gamma_2(t)$ have the same length $l$, then their curvatures are related by the inequality $k_1(t) \geq k_2(t) \geq 0$, $t\in [0, l]$ (under the natural parametrization), and the integral curvature of the first curve is less than $\pi$ (i.e. $\int_0^lk_1(t) dt < \pi$); then, the distance between the points $\gamma_1(l)$ and $\gamma_1(0)$ is not less than the distance between the points $\gamma_2(l)$ and $\gamma_2(0)$, and equality is possible only if $k_1(t) = k_2(t)$ for all $t\in[0, l]$ (see ^[38]).

The integral curvature of an infinite simple convex curve (i.e., a boundary of an unbounded convex plane region) does not exceed $\pi$ (see ^[38]).

Note that the curve $\gamma(t)$ has no self-intersections on each interval $I\subset \mathbb{R}$, where the function $\theta''(t) = k'(t)$ does not change sign (i.e., where the curvature is either strictly increasing or strictly decreasing); see, for example, ^[38]. Therefore, the presence of an infinite number of such self-intersections implies the presence of an infinite number of intervals with a sign-changing (oscillating) derivative of $\theta''(t)$.

7.   One special case

It is easy to verify that for $\beta = 0$, as well as for $\alpha = 0$, the solutions of the system of Eq (4.13) can be explicitly written in the form of elementary functions. As an illustration, we consider the undermentioned case $\beta = 0$ (the case $\alpha = 0$ is considered similarly).

Note that we obtain the following solution of the system of Eq (4.13) for $\alpha = \beta = 0$:

Next, we will consider the solution of the system of Eq (4.13) for $\alpha > 0$ and $\beta = 0$, while $\theta_0$ is not fixed in advance, keeping in mind that the properties of the corresponding curve $\gamma(t) = (y(t), z(t))$ essentially depend on this value.

From the system of Eq (4.13), we obtain that $\theta'(t) = \alpha \cdot \exp(-z(t))$ and $z'(t) = \sin(\theta(t))$, where

Furthermore, by integration, we obtain the following equality:

Using Eq (7.1), we can write the following:

which, after integration, gives the following:

If the solution of the equation $\theta'(t) = \cos(\theta(t))-\cos(\theta_0)+\alpha$ with the initial data $\theta(0) = \theta_0$ is known, then $z(t)$ and $y(t)$ are easily found from equalities (7.1) and (7.2), respectively.

The behavior of the solution of the problem of interest to us significantly depends on the value $a: = \alpha-\cos(\theta_0)$. Since $\alpha > 0$, then $a = \alpha-\cos(\theta_0) > -1$.

If $a = \alpha-\cos(\theta_0) > 1$, then we choose a number $\varepsilon > 0$ such that $\alpha-\cos(\theta_0) > 1+\varepsilon$. Then, $\theta'(t) > \varepsilon$ due to (7.1) and $|\cos(\theta(t))|\leq 1$. Thus, the function $\theta(t)$ is strictly increasing and takes all real values. The turning angle of the curve $\gamma(t) = (y(t), z(t))$ is infinite on the rays $(-\infty, 0]$ and $[0, \infty)$ ($R(-\infty, 0) = \int_{-\infty}^{0} k(t) dt = \infty$, $R(0, \infty) = \int_0^{\infty} k(t) dt = \infty$). The curve $\gamma(t)$ has an infinite number of self-intersections (it is easy to verify that the function $t \mapsto \theta'(t)$ is periodic with the period $2\pi/\sqrt{a^2-1}$). Figure 3(a) shows the graph of the curve $\gamma(t)$ for $a = 3/2$, $\theta_0 = \pi/4$.

If $|a| = |\alpha-\cos(\theta_0)| < 1$, then the image of the function $t \mapsto \cos(\theta(t))$ cannot contain the number $-1$ by virtue of the inequalities $\theta'(t) > 0$ and (7.1). Let $(b, c)$ be the image of the function $t \mapsto \theta(t)$ for some parameters with $|a| < 1$, where $a = \alpha-\cos(\theta_0)$. Since $\alpha > 0$, then $\cos(\theta_0)\neq -1$ (since $\cos(\theta_0)+a = \alpha > 0$, then $\cos(\theta_0) > -a > -1$). It is easy to verify that the differential equation $\theta'(t) = \cos(\theta(t))-a$ has a solution $\theta(t)$, which is defined by the following equality (note that $\tan(\theta_0/2)$ is defined):

where

We see that $\lim\limits_{t \to \infty}\tan(\theta(t)/2) = \sqrt{\frac{1+a}{1-a}}$ and $\lim\limits_{t \to -\infty}\tan(\theta(t)/2) = -\sqrt{\frac{1+a}{1-a}}$. Therefore, we obtain $(b, c) = \left(-2\arctan \left(\sqrt{\frac{1+a}{1-a}} \right)+2\pi n, 2\arctan \left(\sqrt{\frac{1+a}{1-a}} \right)+2\pi n \right)$ for some $n\in \mathbb{N}$ ($n$ is determined by the condition $\theta_0 \in (b, c)$).

The turning angle of the curve $\gamma(t) = (y(t), z(t))$ on the line $(-\infty, \infty)$ is as follows:

Note that the function $a\mapsto 2\arccos(-a)$ strictly increases on the segment $[-1, 1]$ from $0$ to $2\pi$, while it is equal to $\pi$ at $a = 0$.

Figures 3 (c), (d) show the graphs of the curve $\gamma(t)$ for $a = -1/2$, $\theta_0 = \pi/4$ and $a = 1/2$, $\theta_0 = \pi/4$, respectively.

The $\theta(t)$ function has its most unusual properties for $a = \alpha-\cos(\theta_0) = 1$. Since $\alpha > 0$, then $\cos(\theta_0)\neq -1$; therefore, the value of $\tan(\theta_0/2)$ is determined. In this case, $\theta_0 = 2\arctan(\tan(\theta_0/2))+2\pi n$ for a suitable $n\in \mathbb{N}$, and the differential equation $\theta'(t) = \cos(\theta(t))+1$ has a solution $\theta(t)$ defined by the equality $\tan(\theta(t)/2) = t+\tan(\theta_0/2)$. It is clear that the image of the function $t \mapsto \theta(t)$ is an interval of the form $(-\pi+2\pi n, \pi+2\pi n)$, which contains the number $\theta_0$. The turning angle of the curve $\gamma(t) = (y(t), z(t))$ on the line $(-\infty, \infty)$ (i.e., the integral curvature) is equal to $2\pi$.

Let us consider Eq (7.1) for $\cos(\theta_0) = -1$ in more detail. In this case, we obtain $\cos(\theta(t))+1 = \alpha\cdot \bigl(\exp(-z(t))-1 \bigr)$; since $\cos(\theta(t))+1 \in [0, 2]$ for any $t$, then

which is equivalent to the following inequality:

In this case, the equality $z(t) = 0$ is equivalent to $\cos(\theta(t)) = 1$, and $z(t) = -\ln\left(\frac{2+\alpha}{\alpha}\right)$ is equivalent to $\cos(\theta(t)) = -1$.

Expressing $\theta(t)$ from (7.2) and using (7.1), we obtain the following important constraint equation:

which can be rewritten as follows:

Additionally, note that for $a = \alpha-\cos(\theta_0) = 0$, all points $(y, \theta) = (y(t), \theta(t))$ lie on the line $y-\theta+\theta_0 = 0$, and all points $(y, z) = (y(t), z(t))$ lie on the following plane curve:

In this case, the values of $y$ are taken from the maximum interval $I \subset \mathbb{R}$ containing $0$ and not containing points $w$ such that $\cos\Bigl(w +\theta_0\Bigr) = 0$. This curve has no self-intersections, is infinite and convex, and its integral curvature is equal to $\pi$ (as we already know).

In particular, for $\theta_0 = 2\pi n$, $n \in \mathbb{N}$, and $\alpha = \cos(\theta_0) = 1$, this curve has the form $\cos(y)\cdot \exp(z) = 1$ or, equivalently, $z = \ln (1/\cos(y)) = -\ln (\cos(y))$, where $y \in (2\pi n -\pi/2, 2\pi n +\pi/2)$. The graph of this curve is shown in Figure 3(b).

8.   Conclusions

This paper studied important characteristics of geodesics of left-invariant sub-Riemannian metrics on the Cartesian square of a connected two-dimensional non-commutative Lie group, where the metric was defined by the scalar product on the two-dimensional generating subspace of the corresponding Lie algebra. Using the Kovalevskaya exponents, it was proven that the system of equations for geodesics of such a sub-Riemannian metric is not completely integrable in the class of meromorphic functions. The important qualitative characteristics of the corresponding geodesics were found, thus proving the complexity of their behavior in general.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this paper.

Acknowledgments

This research is supported by project FWNF-2022-0003 (the state task to the IM SB RAS).

Conflict of interest

The authors declare there is no conflicts of interest.