Artificial neural networks for stability analysis and simulation of delayed rabies spread models

1.   Introduction

The virus that causes rabies targets the neurological system and, if symptoms start to show, can be lethal ^[1]. Usually, wild animals' bites or scratches are how rabies is transmitted. If wounds or mucosa (such as the mouth and eyes) become contaminated with the saliva of sick animals, it can also spread by direct contact ^[1,2]. An estimated 59,000 people die from rabies annually worldwide; Asia and Africa account for the majority of cases ^[1,3]. The most common human carrier of rabies is dogs. Other animals that have it include cats, foxes, and raccoons ^[1,4]. Even though rabid animals may exhibit odd behaviors, such as aggression and a propensity to bite people or other animals, in addition to excessive drooling, rabies diagnosis is often made through laboratory testing ^[5]. Rabies requires an incubation time following biting, which can range from weeks to years, depending on several factors ^[1]. This phase can last up to 2–3 months. After symptoms occur, there are no recognized treatments for rabies. A person should contact a medical practitioner immediately if they believe they have been exposed to rabies through bites or scratches ^[4]. Dog vaccinations can also be chosen to prevent rabies at its origin. People can receive vaccinations before or after being exposed to rabies ^[1]. To lower the incidence and fatality rate of rabies, it is also critical to raise public awareness and provide education on the prevention of rabies transmission, particularly from domestic dogs ^[1,4]. Epidemiological mathematical modeling has provided insights into the dynamics of rabies transmission and potential disease reduction or eradication strategies. The manuscript's approach to modeling rabies transmission through delay differential equations and artificial neural networks (ANNs) aligns with several real-world applications. For instance, in China, researchers have developed models to evaluate strategies like dog vaccination and culling, finding that limiting dog birth rates and boosting vaccinations effectively curb rabies spread. Similarly, in the Philippines, where rabies transmission occurs between islands, authorities have highlighted the importance of controlling dog transport to prevent interisland spread. The manuscript's piecewise delay differential approach could simulate these regional containment strategies by incorporating boundary conditions for limited mobility, effectively capturing island-based containment measures. In Nepal, where rabies impacts dogs and jackals, the challenge of cross-species transmission necessitates a more nuanced approach. Using singular and non-singular kernel integration in the manuscript's piecewise derivative model can address these crossover dynamics, providing insights into interspecies transmission risks. Furthermore, the application of ANNs in the manuscript enhances predictive accuracy by training, testing, and validating real-world datasets, offering an advantage over traditional models that lack machine learning integration. These real-world examples underscore the manuscript's adaptability and relevance in modeling complex rabies transmission scenarios across diverse settings. Several scholars have conducted mathematical studies on the spread of rabies, particularly in Asia. For instance, Zhang et al. ^[6] created a model to examine the spread of rabies in China. The research also evaluated the effects of dog vaccination and culling on the development of rabies. The model tracked the spread of rabies among human and dog populations. They discovered that restricting dog birth and boosting dog vaccination rates were the best ways to stop the spread of rabies. Based on the developed rabies propagation model across human and dog populations, Chen et al. ^[3] discovered that dog immigration may create an endemic disease even in cases where the disease eventually becomes extinct. They declared that there should be more oversight and better monitoring of dog migration. In the Philippines, Tohma et al. ^[7] reported interisland rabies transmission. They claimed that to stop the disease from spreading, it's critical to recognize that rabies may move between islands and that once the virus is introduced to an island that was previously rabies-free, rabies can become endemic. To stop the spread of rabies, the Philippines should implement ongoing rabies control measures, such as limiting dog transportation. After researching the rabies outbreak in China, Huang, and Li ^[8] created a model of how rabies spreads throughout domesticated and wild dog populations and among humans. Data from Chinese authorities and literature were fitted to the model, and the effectiveness of various suppression techniques was examined. Relative suppression techniques were found to include limiting the number of wild and domesticated dogs born and boosting immunity in domesticated dogs. While dogs were more responsible for the spread of rabies in Nepal, jackals and dogs had a significant impact, according to Pantha et al., ^[9], who observed rabies among human, dog, and jackal populations. They also noted the possibility of interspecies transmission between dog and jackal populations. A few studies also emphasized how crucial it is to use spread control measures in dog populations. According to Asamoah et al., ^[10], for example, mass vaccination of susceptible canines and ongoing use, as well as post-exposure prophylaxis on people, might eliminate the deaths utilizing optimal control. Carroll et al. ^[11] found that major dog vaccination campaigns and population control initiatives are two of the most effective ways to stop the spread. Bornaa et al. ^[12] discovered that rabies can be prevented by limiting contact with infectious dogs, boosting vaccination rates, screening newly adopted dogs, and culling infected dogs. They concluded that these measures should be prioritized over human rabies prevention. Similarly, Renald et al. ^[13] discovered that stray dogs should receive more attention to stop rabies spread.

A system of delay differential equations is another mathematical representation of rabies transmission. A system's inherent ability to respond to an action with a delayed consequence is known as time delay ^[4]. The population growth at time $t$ is shown by a delay differential equation that is dependent on the population at a previous time ^[14]. Recent studies have improved the understanding of attraction-repulsion chemotaxis models, focusing on conditions for boundedness and stability. Columbu et al. ^[15] addressed uniform-in-time boundedness in nonlinear chemotaxis systems, while Jiao et al. ^[16] established global existence for systems with singular sensitivities and proliferation. Li et al. ^[17] demonstrated that specific combined effects in chemotaxis models with production and consumption dynamics ensure boundedness. These findings enhance stability predictions for complex biological systems influenced by attraction and repulsion forces. Abdulmajid and Hassan created a SIV (susceptible-infected-vaccinated) epidemic model with delay ^[2] to assess the impact of time delays for the incubation period and controls on the spread of rabies in canine and human populations. This study is an illustration of delay-incorporated rabies spread modeling research. It was discovered that the best ways to eradicate rabies were to boost dog vaccination rates and reduce the number of puppies born. This study also developed and examined a model of the transmission of rabies in dog and human populations as a system of delay differential equations with delay effects. The vaccination period is also a time delay that influences the model of how rabies spreads and the incubation period. Finding the most effective ways to stop or completely stop the spread of rabies is one of our main research goals, along with analyzing the stability of the delay system and the impact of two delays on it. The thought is to enhance earlier studies on the intricate nonlinear dynamics of rabies transmission.

Recent studies illustrate the effectiveness of neural networks and mathematical models in handling complex dynamics with delays across various fields. Huang et al. ^[18] and Liu ^[19] explored stability in neural networks influenced by mixed and time-varying delays, advancing our understanding of delayed systems. Long and Gong ^[20] analyzed the stability of Nicholson's blowflies equation under multiple delays, contributing to population dynamics modeling. Sabir et al. ^[21,22] applied neural networks to language learning and astrophysics, demonstrating versatility in complex problem-solving. Lastly, Kumar et al. ^[23] modeled Prandtl fluid flow using neural networks, showcasing their utility in fluid dynamics. Together, these works highlight the adaptability of neural and delay models across diverse scientific challenges.

Fractional calculus has emerged as an alternative mathematical tool for describing models with nonlocal behavior, offering additional interest and flexibility ^[24,25]. This approach allows for a more accurate model and test data fitting than integer-order models. Historical memory and global knowledge of physical phenomena are captured using fractional differential equations, providing a more comprehensive representation of the dynamics of physical phenomena than integer-order models. There are several applications in the literature for nonlocal operators. Nonlocal operators have found applications that are addressed in various fields of applied mathematics such as disease models ^[26], biomathematics and chaotic ^[27], engineering and stochastic models ^{[28,29,30,31]}, and various other applicable fields of sciences in the literature of fractional differential equations ^{[32,33,34,35,36]}. The fractional techniques have been applied to the generalized classical models of the dengue disease model. Indeed, the fractional technique is helpful in generalizing classical models of the dengue model to a large extent. As a result of this modification, we hope to improve our understanding of epidemic trends and the prediction of intervention strategies. Several fractional order models have been developed and found to be extremely useful in identifying specific patterns in the development of patient illness and a better fit for the data. To devise novel therapies tailored to patients' needs, clinicians can use data from the universal fractional order system as a starting point by fitting their data to the most appropriate fixed index. Consequently, the fractional differential equation applying to the disease models gives accurate and exact solutions. To get precise results, choosing a meaningful fractional index based on available accurate data in the literature is essential. A novel approach involving piecewise differentiation and integration has been proposed. This method introduces classical and global piecewise derivatives, accompanied by application examples. Despite this, it should be noted that only real-world problems that follow the crossover properties of these two functions can be modeled, albeit with some limitations. For example, in a real-world situation, these two functions cannot establish the time the crossover took place. The Mittag-Leffler and exponential functions' crossover properties are recognized as powerful mathematical tools to depict real-world problems. As a result of the investigation of crossover problems, various operators were developed, including fractal derivatives, non-integer-order derivatives with singularity and non-singularity kernels, fractal-fractional operators, and others ^[37,38,39]. It has been observed that, despite stochastic equations incorporating randomness, crossover dynamics remain unsolved in many models, including infectious diseases and complex advection problems ^[40,41]. The Caputo-Fabrizio and Atangana-Baleanu derivatives cannot be used to reproduce real-world issues that display distinct processes from those described by the extended Mittag-Leffler function and exponential decay function. Suppose a real-world situation initially exhibits a power law process, followed by a fading memory process. In this case, neither the general Mittag-Leffler nor the exponential decay functions can adequately describe the observed behavior. The researchers have established a pioneer work on applying different approaches to the fractional order model via time delay term, chaos theory, and bifurcation ^[42,43,44].

2.   Model formulation

We reconsidered the rabies disease model ^[4] in the framework of piecewise differential and integral and analyzed its crossover behaviors. Two populations—the human and dog populations—are included in the model that has been created, and they both reside in the same setting. The susceptible human population ($S_H$), the infected human population $(I_H)$, and the vaccinated human population $(V_H)$ comprise the three subpopulations that make up the human population. A susceptible dog population $(S_D)$, an infected dog population $(I_D)$, and a vaccinated dog population $(V_D)$ comprise the three subpopulations that make up the dog population. The following vital presumptions form the basis of the model's construction:

1) There are no migrations into or out of the system. The only factors affecting population size are births and deaths.

2) Only rabid dogs can spread the rabies virus. There is no rabies transmission between susceptible dogs and diseased humans, nor between susceptible humans and afflicted humans.

3) Vaccination is thought to confer a long-time immunity. As a result, populations that have received vaccinations do not lose immunity.

4) New infections do not always arise from contact with affected dogs. Rather, there is a period of incubation.

5) Immunity is not immediately acquired by vaccination. The vaccination must work for a certain amount of time before it may provide immunity.

6) Natural death is a possibility during incubation and immunization.

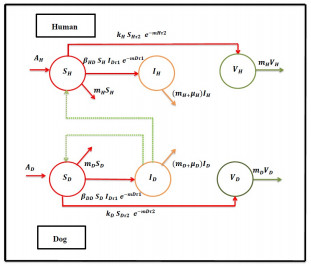
In this case, natural death is taken to occur randomly. Figure 1 details the dynamic of rabies spread between human and canine populations. As depicted in Figure 1, the average annual human birth rate $(A_H)$ increases the susceptible human population. It is lowered by vaccination at rate $k_HS_{H_{\tau_2}}e^{-m_H\tau_2}$, natural death at rate $m_H$, and infection by contact with infected dogs at rate $\beta_{HD}S_HI_{D_{\tau_1}}e^{-m_D\tau_1}$. The incubation delay in this case is $\tau_1$, while the vaccine delay is $\tau_2$. Moreover, $e^{-m_D\tau_1}$ represents the likelihood that rabid dogs will die naturally within the time frame $[0, \tau_1], e^{-m_H\tau_2}$ represents the likelihood that susceptible humans will die naturally within the time frame $[0, \tau_2], \beta_{HD}$ represents the rate of transmission between susceptible humans and infected dogs, and $k_H$ represents the human vaccination rate. The rate of transmission of the infection from susceptible humans to infected dogs is $\beta_{HD}S_HI_{D_{\tau_1}}e^{-m_D\tau_1}$. On the other hand, the rate of natural and rabies-related fatalities is $m_H$ and $\mu_H$, respectively, resulting in a drop in the number of infected people. The rate at which vulnerable persons are vaccinated is $k_HS_{H_{\tau_2}}e^{-m_H\tau_2}$; the rate at which natural death occurs is $m_H$.

The average annual dog birth rate $(A_D)$ increases the susceptible dog population. It is lowered by vaccination at rate $k_DS_{D_{\tau_2}}e^{-m_D\tau_2}$, the rates of infection by contact with diseased dogs are $\beta_{DD}S_DI_{D_{\tau_1}}e^{-m_D\tau_1}$ and natural death at $m_D$. In this case, the likelihood that susceptible dogs will die naturally within the time range $[0, \tau_2]$ is $e^{-m_D\tau_2}$; the rate of transmission between susceptible dogs and infected dogs is $\beta_{DD}$; and the vaccination rate of dogs is $k_D$. The rate at which the number of infected dogs increases is $\beta_{DD}S_DI_{D_{\tau_1}}e^{-m_D\tau_1}$; the rate at which the number of infected dogs decreases is $m_D$. The rate at which rabies-related deaths occur is $\mu_D$. At rate $k_DS_{D_{\tau_2}}e^{-m_D\tau_2}$, vaccination of susceptible dogs increases the population of vaccinated dogs; at rate $m_D$, natural death reduces it. The description of each variable and model parameter is compiled in Table 1.

The considered model in the sense of piecewise derivative having singular and non-singular kernels with order $0 < \nu\leq1, \ \zeta\in[0, T]$ can be expressed as follows:

having initial condition

$I_H(0) \geq 0, V_H(0) \leq 0$, and $V_D(0) \geq 0$, respectively, are the initial values of $I_H(t), V_H(t)$, and $V_D(t)$. The historical functions of $S_H(t), S_D(t)$, and $I_D(t)$ are $\psi_1(t) \geq 0, \psi_2(t) \geq 0$, and $\psi_3(t) \geq 0$, respectively, inside the interval $[-\tau_2, 0]$, the functions of $\psi_1(t)$ and $\psi_2(t)$ are continuous, and $\psi_3(t)$ is a continuous function inside the interval $[-\tau_1, 0]$.

The flow chart diagram of the considered model is given in Figure 1. To describe Eq (2.1) more precisely, we can write it as follows:

where $^{C}_0 {\mathfrak{D}}_\zeta^\nu$ and $^{C{\mathbb{ABC}}}_0 {\mathfrak{D}}_\zeta^\nu$ are Caputo and Atangana-Baleanu Caputo ($\mathbb{ABC}$) derivates, respectively.

Motivated by the above literature, piecewise fractional operators are useful for capturing crossover and abrupt dynamics in system dynamics, which is why we utilized them in our study. This paper examined a set of differential equations under the Caputo and Atangana-Baleanu piecewise fractional operator that characterizes the crossover dynamics of the dengue model. In particular, we applied various fractional operators to various system intervals and offered a qualitative analysis for every subinterval. We employed the Ulam Hyers (UH) stability analysis to evaluate stability. To generate approximation solutions that can accommodate dynamics of both integer and rational orders, we also looked into the use of piecewise terms and fractional orders in the system's final step. The advantage of this paper lies in its novel approach to modeling rabies transmission dynamics through the integration of delay differential equations, piecewise derivatives with singular and non-singular kernels, and ANNs. Unlike traditional models, this work uniquely accounts for delay effects in vaccination efficacy and incubation duration, providing a more realistic simulation of rabies spread. By applying a piecewise derivative framework, this study captures nuanced crossover behaviors often overlooked in existing models, allowing for a more detailed exploration of interspecies transmission risks and control strategies. Furthermore, incorporating ANNs enables the model to enhance predictive accuracy by training on real-world datasets, setting this approach apart from conventional methods lacking machine learning integration. The neural network approach is used, and the dynamics of the proposed model are as follows:

The rest of the work is organized as follows: In Section 3, we discuss the basic results used in the paper. The existence and uniqueness results are established by using the fixed point approach in Section 4. The numerical approach is analyzed for the considered model (2.2) with fractional order in Section 5. Simulation of the proposed model has been discussed along with ANN and we mention different dynamics graphically in Section 6. Finally, we conclude our work in Section 7.

3.   Basic results

Here, we shall provide some basic definitions for fractional derivatives and integrals of $\mathbb{ABC}$ and Caputo.

Definition 3.1. ^[24] The derivative of a function $\mathbb{W}(\zeta)$ with respect to the $\mathbb{ABC}$ operator, given the condition that $\mathbb{W}(\zeta)$ belongs to the space $\mathcal{H}^1(0, \tau)$, is defined as below:

Replace ${E}_\nu\bigg[\frac{-\nu}{1-\nu}\bigg(\zeta-\theta\bigg)^\theta\bigg]$ with ${E}_1 = \exp\bigg[\frac{-\nu}{1-\nu}\bigg(\zeta-\theta\bigg)\bigg]$ in Eq (3.1) to obtain the Caputo-Fabrizio differential operator. Additionally, it is noted that ${}^\mathbb{ABC}{_0{{D}}}_\zeta^\nu[constant] = 0$. In this context, the normalization operator denoted as ${ABC}(\nu)$ is expressed as $\mathbb{ABC}(0) = \mathbb{ABC}(1) = 1$. The symbol ${K}_\nu$ also signifies the Mittag-Leffler function, a generalized form of the exponential function.

Definition 3.2. ^[24] If $\mathbb{W}(t)\in L[0, T]$, then the fractional integral in the $ABC$ sense is expressed as:

Definition 3.3. ^[25] Consider the function $\mathbb{W}(\zeta)$. For the definition of the arbitrary order derivative in the Caputo sense concerning $\zeta$, it is expressed as:

where $\Gamma(\cdot)$ represents the gamma function.

Definition 3.4. Consider the function $\mathbb{W}(\zeta)$ to be differentiable. For the definition of the Caputo and $\mathbb{ABC}$ fractional piecewise derivative, as introduced in ^[24], it is expressed as:

where, $^{PC\mathbb{ABC}}{0}{D}{\zeta}^\nu \mathbb{W}(\zeta)$ represents the Caputo derivative for $0 < \zeta \leq \zeta_1$ and the fractional $\mathbb{ABC}$ derivative for $\zeta_1 < \zeta \leq T$.

Definition 3.5. Consider the function $\mathbb{W}(\zeta)$ to be differentiable. For the definition of fractional Caputo and fractional $\mathbb{ABC}$ piecewise integration, as introduced in ^[24], it is expressed as:

where, $^{PC\mathbb{ABC}}{0}{I}{\zeta}\mathbb{W}(\zeta)$ denotes Caputo singular kernel integration for $0 < \zeta\leq \zeta_1$ and $\mathbb{ABC}$ integration for $\zeta_1 < \zeta \leq T$.

4.   Qualitative analysis

Now, we want to prove the existence and uniqueness of the solution for the considered piecewise derivable function. Further elaborating the system (2.2), we can write it as follows:

is

where

where, $i = 1, 2, 3, 4, 5, 6$, now, we take $\infty > T\geq \zeta > 0$, then $X = (C[0, T]\times{R}^6, R_+)$ is a Banach space. Further, $M = X_1\times{X_2}\times{X_3}\times{X_4}\times{X_5}\times{X_6}$ is also a complete norm space endowed with norm

which can be written as in Eq (4.1).

To obtain the desired outcome, we take into account the nonlinear operator's growth condition:

(C1) $\exists \; L_{\mathbb{W}} > 0$; $\forall \; K, \ \bar{\mathbb{W}}\in {K}$, we have

(C2) $\exists \; C_{K} > 0 \; \& \; M_{K} > 0,$

Theorem 4.1. If $H$ is piecewise continuous on the subintervals $0 < \zeta \leq \zeta_1$ and $\zeta_1 < \zeta \leq T$ within the interval $[0, T]$, it also satisfies condition $(C2)$. The piecewise problem (2.2) has at least one solution on each subinterval.

Proof. Let us define a closed subset in both subintervals of $0$ to $T$ as ${G}$ of ${E}$ by using the Schauder fixed-point theorem in the following manner:

Next, we present the following operator: Using (4.1) as well as $\mathcal{T}: {G} \rightarrow {G}$,

and on any $\mathbb{W}\in {G}$, we get

Based on the previous equation, $\mathbb{W}\in {G}$. $\mathcal{T}({G})\subset {G}$, as a result, demonstrates the completeness and closeness of $\mathcal{T}$. In addition, for total consistency, we write as follows: Assume that $\zeta_z < \zeta_j \in [0, \zeta_1]$ is the first interval of the Caputo sense:

Next, from (4.4), we get $\zeta_z\rightarrow \zeta_j$, then,

So, $\mathcal{T}$ is equi-continuous in $[0, \zeta_1]$ interval. Next, we take the other interval $\zeta_z, \zeta_j \in [\zeta_1, T]$ in the $\mathbb{ABC}$ sense as

Next, as (4.5), we get $\zeta_z\rightarrow \zeta_j$, then

$\mathcal{T}$ is therefore equi-continuous in the interval $[\zeta_1, T]$. As a result, the mapping $\mathcal{T}$ is equi-continuous. The operator $\mathcal{T}$ is bounded, uniformly continuous, and continuous using the Arzelà-Ascoli theorem. As a result, the piecewise derivable problem (2.2) has at least one solution on each subinterval according to Schauder's fixed-point theorem. □

Theorem 4.2. With $(C1)$, the proposed model has a unique solution if $\mathcal{T}$ is a construction operator.

Proof. As we have defined an operator $\mathcal{T}: {G}\rightarrow {G}$ to be piecewise continuous, consider $\mathbb{W}$ and $\bar{\mathbb{W}} \in {G}$ on $[0, \zeta_1]$ in the Caputo sense, as follows:

From (4.6), we have

Thus, $\mathcal{T}$ is bounded. Thus, in the context of the Banach contraction theorem, the issue under consideration has a unique solution inside the specified subinterval. Next, in terms of the $\mathbb{ABC}$ derivative, for the other interval $\zeta\in[\zeta_1, T]$ as

or

$\mathcal{T}$ is a contraction as a result. Accordingly, the issue under consideration has a unique solution in the specified subinterval in the sense of the Banach contraction theorem. The piecewise derivable issue thus has an unconventional resolution on each subinterval by Eqs (4.7) and (4.9). □

4.1.   Stability analysis

To ensure the stability of the considered model, we need the following analysis:

Definition 4.1. The model (2.1) under consideration is U-H stable; if each $ß > 0$, the following inequality will be held.

A unique solution will have $\overline{\mathbb{W}}\in Z$ and a constant $\aleph > 0$,

Moreover, the inequality above can be written as follows if we consider an increasing function $\theta:[0, \infty)\rightarrow R^{+}$.

If $\theta(0) = 0$, the obtained solution will be generalized U-H stable (G-U-H).

Remark 4.1. Given that a function $\theta\in C(\mathcal{T})$ satisfies $\theta(0) = 0$ and is independent of $\mathbb{W}\in\mathscr{W}$, the following can be concluded:

Lemma 4.1. Suppose the following function:

The solution for Eq (4.12) can be

Theorem 4.3. Lemma 4.1 implies that the solution to model (2.1) is both G-U-H and U-H stable if $\frac{L_{f}\mathcal{T}^{\nu}}{\Gamma(\nu)} < 1$.

Proof. We can determine that $\overline{\mathbb{W}}\in \mathscr{W}$ is a unique solution of (2.1) if $\mathbb{W}\in \mathscr{W}$ is a solution of (2.1).

Case 1: For $\zeta\in\mathcal{T}$, we obtain

Along with the following:

Case 2:

Using $\Lambda = \left[\frac{(1-\nu)\Gamma(\nu)+T_{2}^{\nu}}{\mathrm{ABC}(\nu)\Gamma(\nu)}\right]$, and further calculation, we have

or

We use

Now, from inequalities (4.16) and (4.17), we have

As a result, we may say that model (2.1) has a U-H stable solution. Furthermore, we obtain the following results in (4.18) if we replace $ß$ with $\theta(ß)$:

Thus, the results show that the system under consideration is G-U-H stable because $\theta(0) = 0$. □

5.   Numerical scheme

The following numerical approach is shown for the piecewise differentiable issue (2.2). We shall create a numerical scheme for the two subintervals of $[0, T]$ in the Caputo and $\mathbb{ABC}$ senses. The integer order numerical approach used in ^[24] will be the foundation for our piecewise derivative. We express it as follows by using the piecewise integration to solve Eq (2.2) for the Caputo and $\mathbb{ABC}$ formats:

where $^CH_z(\zeta) = ^CH_z(S_H, I_H, V_H, S_D, I_D, V_D, \zeta)$ and $^\mathbb{ABC}H_z(\zeta) = ^\mathbb{ABC}H_z(S_H, I_H, V_H, S_D, I_D, V_D, \zeta)$ are the left-hand side of Eq (2.1) for $z = 1, 2, 3, 4, 5, 6$, also given in Eq (2.2). The scheme for the system's first equation, (5.1), will be derived, and the remaining compartments will be treated similarly. When $\zeta = \zeta_{n+1}$,

writing Eq (5.2) in the Newton interpolation approximation given in ^[24] is as follows:

We can write the Newton interpolation estimate for the remaining compartments as follows:

Here

and

6.   Numerical simulation and discussion with ANN

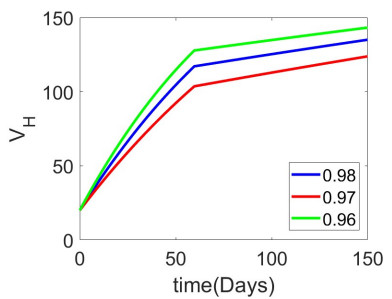
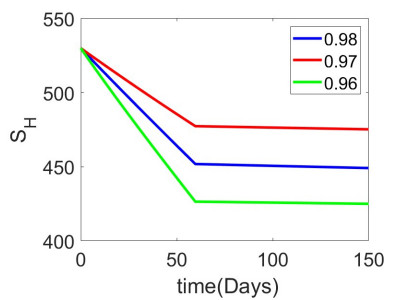
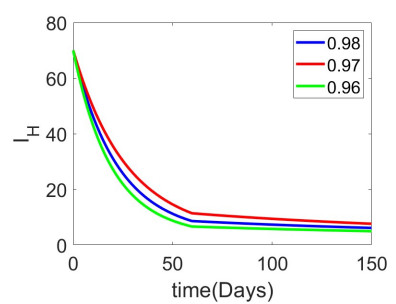
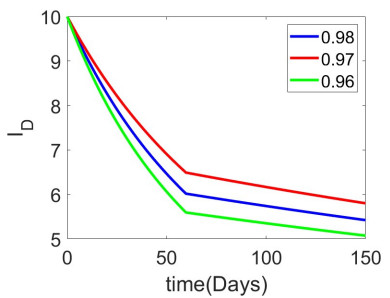
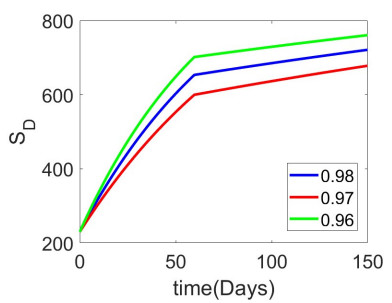
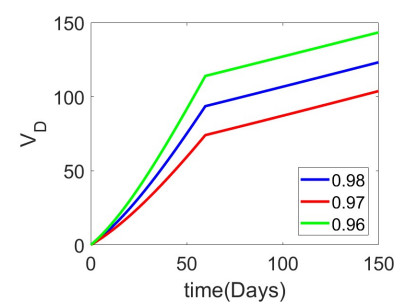
We have implemented an ANN to analyze the piecewise derivative models of rabies transmission. The datasets are taken from the piecewise Adams-Bashforth numerical methods. ANN trains the datasets, and the model's accuracy is shown in the figures. In the context of rabies disease, primarily transmitted by dogs to humans, Figure 2 shows how the illness spreads to human populations and eventually dies out after about eight years, with no surge in the number of cases because there is little contact between susceptible humans and canine rabies. As seen in Figure 3, the proportion of susceptible people gradually declines, suggesting that high vaccination rates cause many susceptible people to move into the vaccinated subpopulation. Figure 4 shows that the number of susceptible dog populations gradually declines. Figure 5 shows that while the number of vaccinated people continues to rise, its growth is slower each time, suggesting that an equilibrium condition will eventually be reached. Figure 6 shows that the number of instances of infection in dog populations increases, albeit to less than thirty within the first years. After that, the infection progressively declines until the disease eventually goes extinct in roughly ten years. Additionally, Figure 7 illustrates how a high vaccination rate contributes to a rising number of vaccinated dogs, correlated with a declining susceptible dog population.

We simulate the outcomes of the preceding algorithms for the different categories in (27)–(32) using Matlab and the parameter values from Table 2, as shown in Figures 2–7.

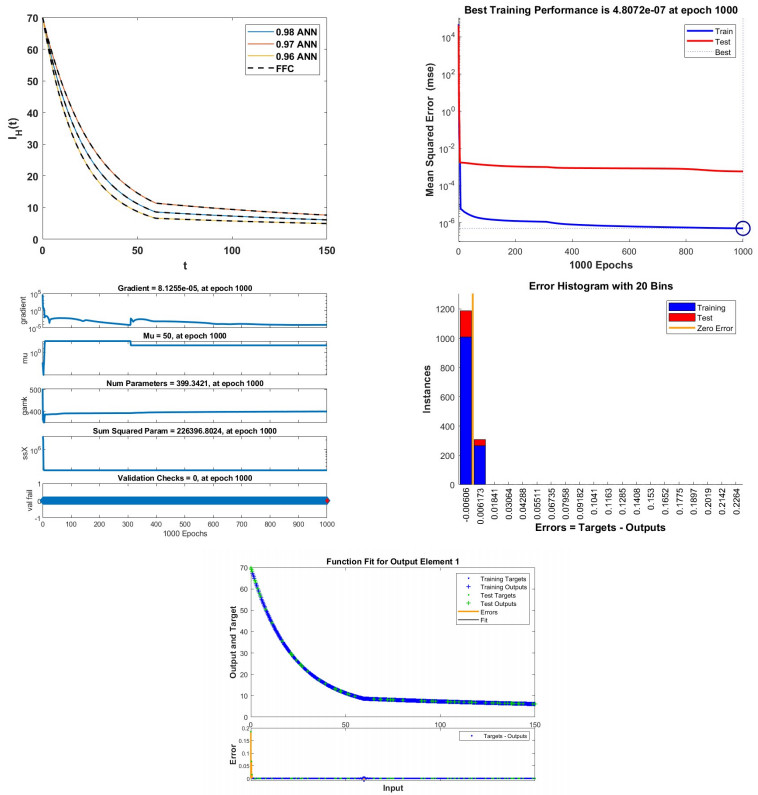
The model's dataset identifies three groups: 70% are designated for training, 15% for testing, and 15% for validation. Each category's fractional order is distinct. The approach of ANN using the Adam Bashforth method is shown in Figure 8 (a). Figure 8 (b) displays the model's performance at epoch $1000$, with mean square errors of $4.8072e-07$. Figure 8 (c) displays the training state. Figure 8 (d) shows the error histogram, and $-0.00606$ is the best number we could discover in this instance. Figure 8 (e) displays the errors in the exact figure and the best fit of the training and testing data.

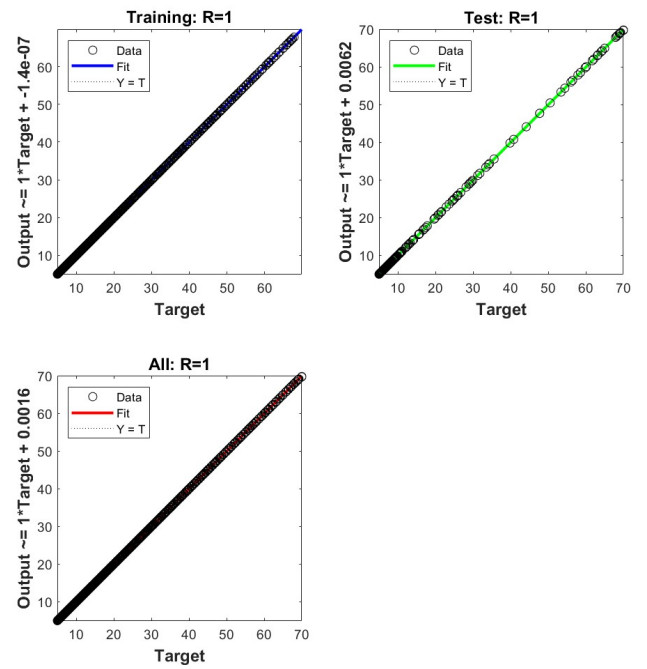
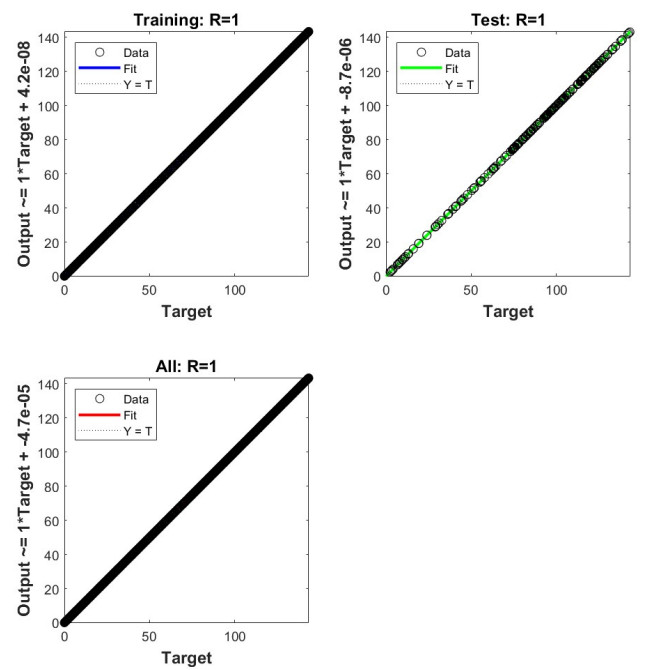
Figure 9 shows the regression of the model under examination for all data, testing data, and training data. The data's obvious placement on the regression line suggests that the final solution was accurately trained. The value of R is about 1.

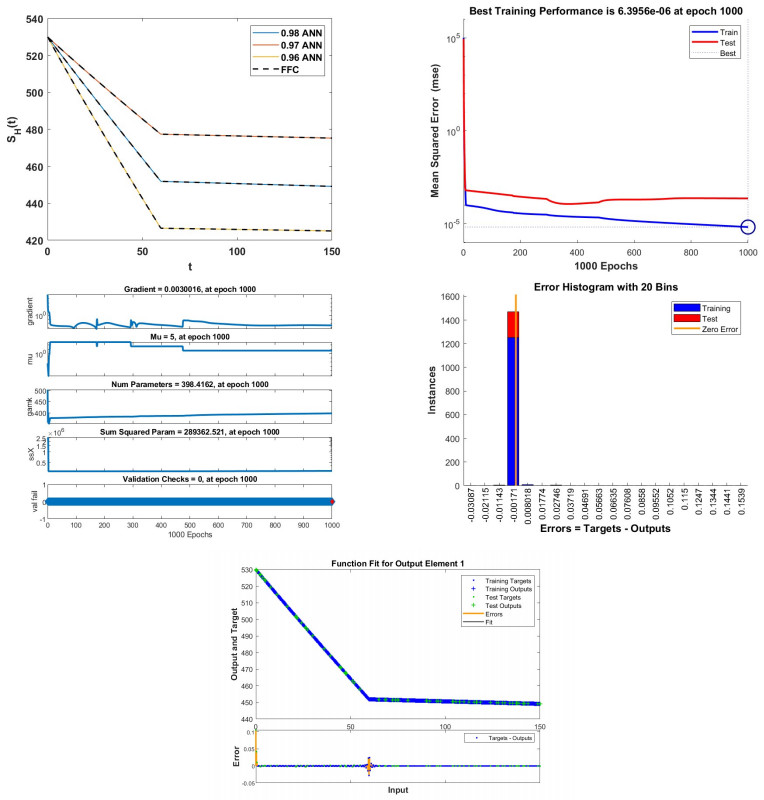
The approach of ANN using the Adam Bashforth method is shown in Figure 10 (a). Figure 10 (b) displays the performance of the studied model at epoch $1000$, with mean square errors of $6.3956e-06$. The state of training is shown in Figure 10 (c). The state of training is displayed in Figure 10 (d). The error histogram is given in Figure 10 (e), with the best value we could discover in this example being $-0.00171$. Figure 10 (e) displays the optimal fit of the training and testing data and errors, as indicated by the exact figure.

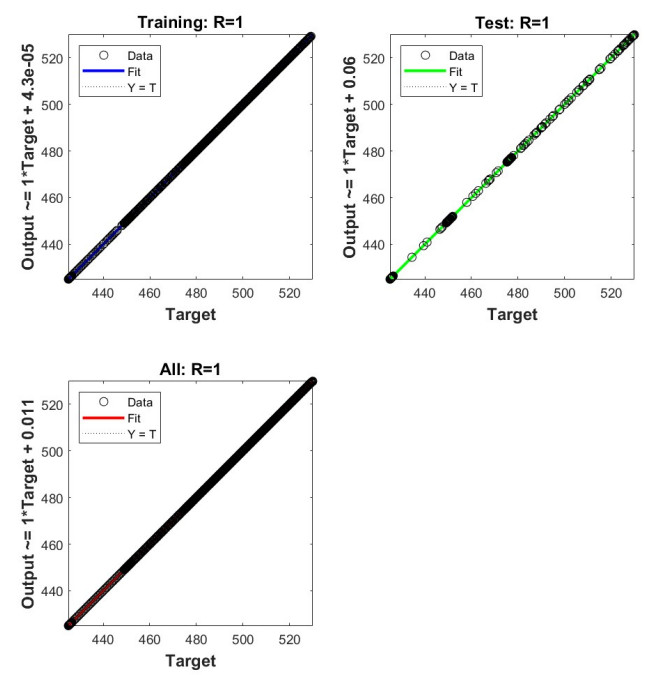
Figure 11 shows the regression of the model under examination for all data, testing data, and training data. The data's prominent placement on the regression line suggests that the final solution was accurately trained. The value of R is about 1.

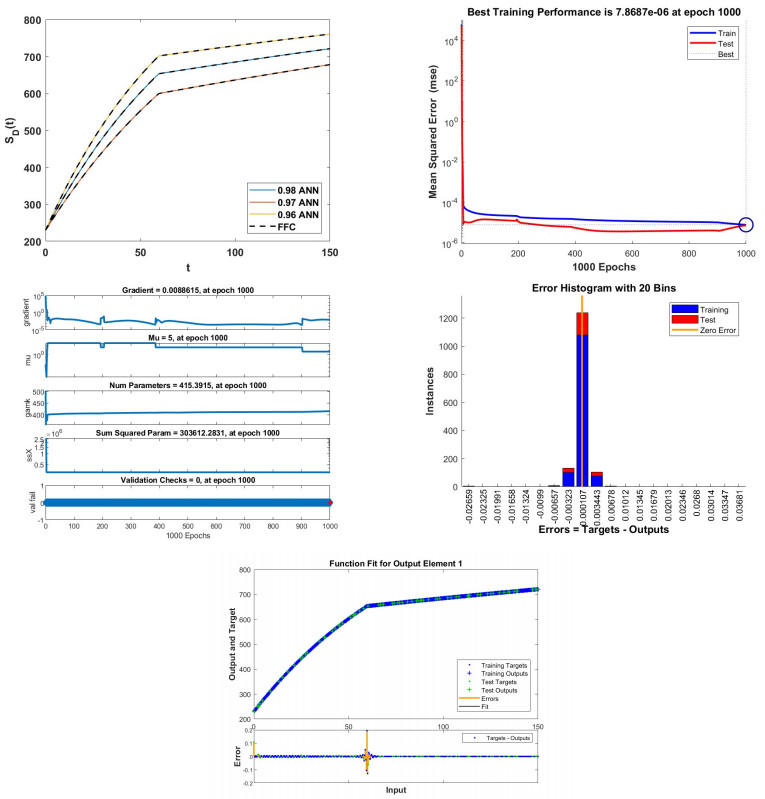
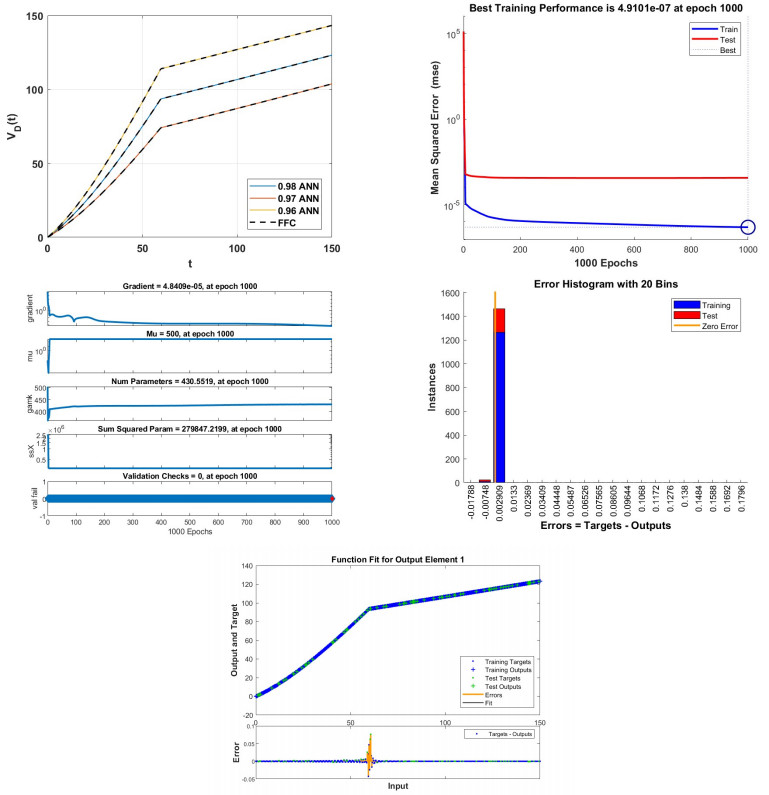
The approach of ANN using the Adam Bashforth method is shown in Figure 12 (a). Figure 12 (b) displays the performance of the studied model at epoch $1000$, with mean square errors of $7.8687e-06$. The state of training is displayed in Figure 12 (c). The state of training is displayed in Figure 12 (d). The error histogram is displayed in Figure 12 (d), and $0.000107$ is our best result. Figure 12 (e) displays the best fit of the training and testing data along with the errors in the same figure.

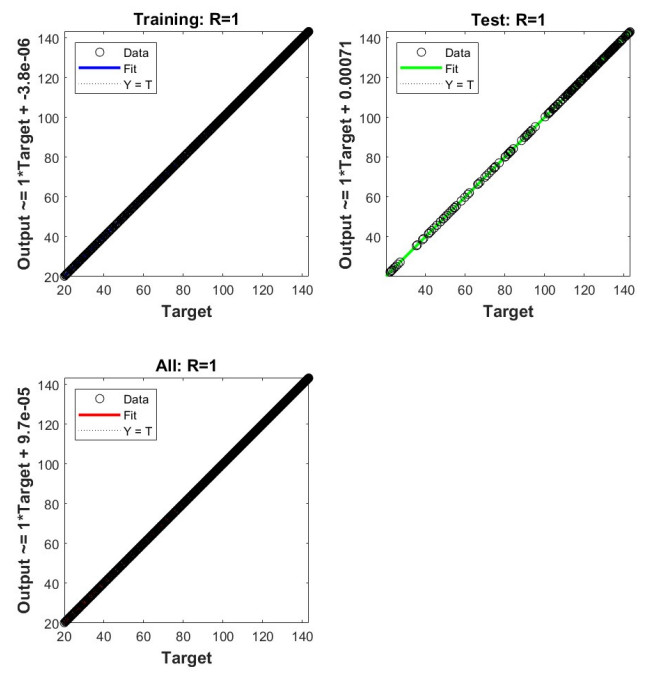
Figure 13 displays the regression for all testing and training data for the model under discussion. The data's obvious placement on the regression line suggests that the final solution was accurately trained. The value of R is about 1.

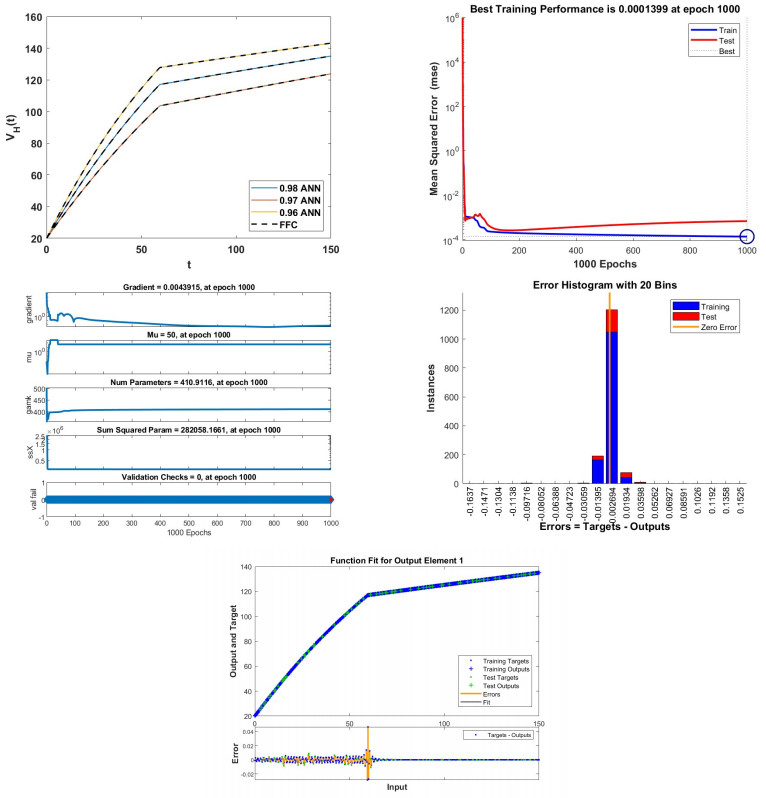
The approach of ANN using the Adam Bashforth method is shown in Figure 14 (a). Figure 14 (b) displays the performance of the studied model at epoch $1000$, with mean square errors of $0.0001399$. The state of training is displayed in Figure 14 (c). The error histogram is displayed in Figure 14 (d), and $0.002694$ is our best result. Figure 14 (e) displays the best fit of the training and testing data and the errors mentioned in the figure.

Figure 15 illustrates the regression of the model under examination for all testing and training data. The data's obvious placement on the regression line suggests that the final solution was accurately trained. The value of R is about 1.

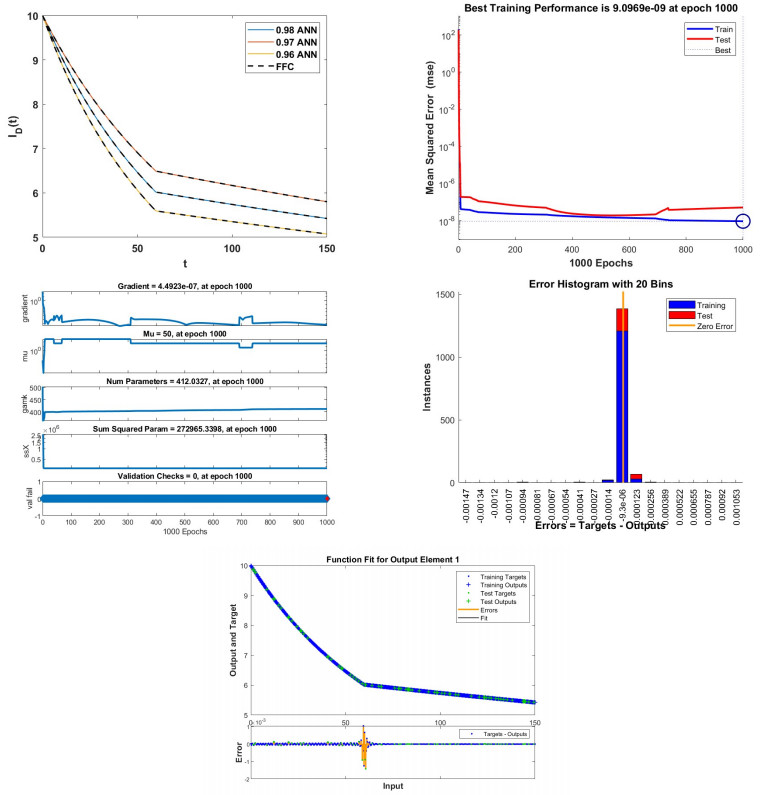
The approach of ANN using the Adam Bashforth method is shown in Figure 16 (a). The performance of the studied model at epoch $1000$ is displayed in Figure 16 (b), with mean square errors of $9.0969e-09$. Figure 16 (c) displays the training state. The error histogram is displayed in Figure 16 (d), and $-9.3e-06$ is the best result we obtain. Figure 16 (e) displays the errors and the best fit of the training and testing data.

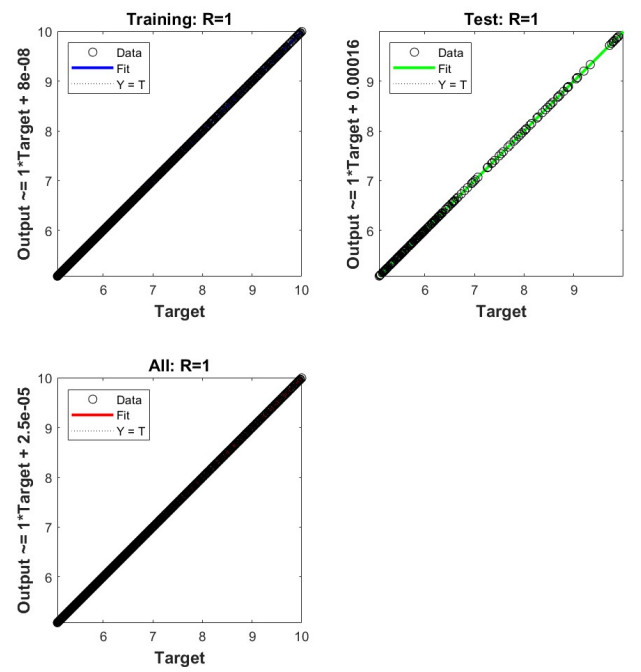
The regression of the model under investigation for all training, testing, and data is displayed in Figure 17. The resultant solution was accurately trained, as evidenced by these graphs that show where the data falls on the regression line. The value of R is about 1.

The approach of ANN using the Adam Bashforth method is shown in Figure 18 (a). Figure 18 (b) displays the performance of the studied model at epoch $1000$, with mean square errors of $5.2036e-13$. Figure 18 (c) displays the training state. The error histogram is displayed in Figure 18 (d), and $1.38e-07$ is the best result. Figure 18 (e) displays the errors and the best fit of the training and testing data.

The regression of the model under investigation for all training, testing, and data is displayed in Figure 19. The resultant solution was accurately trained, as evidenced by these graphs that show where the data falls on the regression line. The value of R is about 1.

7.   Conclusions

This study aimed to examine the dynamics of a rabies epidemic model using a unique piecewise derivative approach based on the Caputo and ABC operators. A piecewise derivative solution for the disease model outlined in our paper was investigated to establish its existence and uniqueness. We used the piecewise Newton polynomial approach to approximate the solution. The paper introduces a numerical method for piecewise derivatives using singular and non-singular kernels. We did numerical simulations of the piecewise rabies model at different fractional orders and found that piecewise operators have better dynamics than classical ones. Using ANN approaches on a piecewise model, the dataset is split into training, testing, and validation sets. A detailed analysis is conducted for each category. Our work advances the concept of piecewise derivatives by providing a clearer understanding of crossover behavior dynamics. A significant outcome of our simulations is that greater vaccine efficiency resulted in a greater recovery rate. We identified substantial correspondences by analyzing large quantities of numerical and graphical data. Research into incorporating additional factors in this study is an exciting avenue for future research. These factors may include evolving vaccination strategies, weather, or socioeconomic variables to improve the model's predictive capabilities. As a result of this holistic approach, we are likely to develop more effective strategies for controlling and preventing the disease.

Author contributions

Ramsha Shafqat: conceptualized and designed the study, supervised the research process, conducted the investigation, prepared the original draft of the manuscript, validated the results, reviewed and edited the manuscript for clarity and accuracy, contributed to the development of the software tools used in the study, and secured funding; Ateq Alsaadi: responsible for data curation, formal analysis, visualization, managed the project, overseeing research activities, and ensuring the timely completion of tasks. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-259).

Conflict of interest

The authors declare no conflict of interest.