Well-posedness of a nonlinear stochastic model for a chemical reaction in porous media and applications

1.   Introduction

Solute transfer in porous substances is a topic that chemists, geologists, and environmentalists are all interested in. Convection, diffusion, and potential chemical reactions that the solutes may go through are the phenomena that impact solute transport. Most of the mathematical modeling literature for solute transportation in porous medium encompass deterministic diffusion and conviction equations, see for example ^[2,10,11,15] and the references therein. The earliest rigorous mathematical investigation for this type of model dates back to ^[15], when the authors investigated a deterministic linear model for convection, adsorption, diffusion, and chemical reaction in perforated materials. In ^[11], the authors proposed expansions to nonlinear models, including linear diffusion, and chemical reaction equations with nonlinear chemical flow across the skeleton's surface. Related models dealing with Homogenization of reactive flows in porous media was discussed ^[2,10]. Nonlinear chemical reactive fluxes have been widely explored in well-posedness of elliptic linear and nonlinear PDEs (among others, we refer to ^[6,7,13]). However, stochastic differential equations account for the inherent randomness impacting the solute's movement through a porous medium. In ^[4], Bessaih et al. explored the asymptotic analysis and well-posedness of stochastic systems in diffusion-convection flows. Their system integrates a deterministic diffusion equation with a stochastic linear convection equation. Additionally, in ^[17], the author examined the asymptotic behavior of a nonlinear stochastic model featuring nonlinear random forces for chemical reactive fluxes in porous media.

We aim to establish the existence and uniqueness of strong probabilistic solutions, demonstrate positivity, and conduct numerical simulations for the nonlinear stochastic version of the model in ^[11] (see also ^[17]). Specifically, we examine a stochastic model of chemical reactive flows subject to nonlinear external random fluctuations within porous media. A porous medium is a material made of holes or pores, and the skeletal part of a porous medium is called a matrix or a frame. We consider a situation where chemical substances are dissolved in a fluid and transported by diffusion through a porous medium. These chemicals adsorb onto the surface of the skeleton and react with substances bound to the surface of the skeleton. Adsorption and reaction mechanisms continuously impact solute concentrations in fluids and skeletal surfaces. In addition, we suppose that exogenous nonlinear random forces influence the solute concentration in the fluid. A porous medium is described mathematically as a perforated domain where the perforations represent the obstacles in the porous medium. The perforated domain consists of both the fluid phase (pores) and the solid phase (skeleton). Diffusion occurs in the fluid phase, while reactions occur on the solid phase's surface. The model includes a stochastic diffusion system in the fluid phase, a stochastic response system on the skeleton's surface, and a boundary condition that connects the two. It is important to note that well-posedness, positivity, and numerical simulations have not yet been addressed for this type of nonlinear stochastic model. However, some results related to the analysis of nonlinear stochastic evolution equations and nonlinear parabolic stochastic differential equations can be found in ^[1,16,25] and the references therein. This study represents a significant advancement in the modeling of solute transport in porous media by integrating stochastic elements and addressing nonlinear chemical reactions. Its contributions are valuable across multiple disciplines, offering both theoretical and practical benefits. However, the complexity and computational demands of the models, along with the challenges in parameter estimation and potential limitations in generalization, should be considered when applying these findings to real-world scenarios.

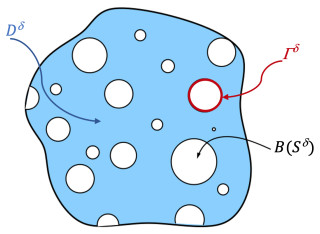
Let $D \subset \mathbb{R}^{n}$ be an open and bounded set, $S^{\delta}$ is small hole (smooth enough) in $\mathbb{R}^{n}$ of diameter $\delta$, where $\delta>0$ is small number that allows to go to zero, and $B(S^\delta)$ be is the set of all periodically distributed holes $S^{\delta}$ in $\mathbb{R}^{n}$ such that $B(S^\delta) \cap \partial D = \emptyset$. Define the perforated domain as $D^{\delta} = D\cap B(S^\delta)$, where we denote by $\Gamma^{\delta}$ the boundary $\partial(\mathbb{R}^n\backslash B(S^\delta))$, therefore, $\partial D^{\delta} = \partial D\cup\Gamma^{\delta}$. An illustration of the domain $D$ and holes are presented in Figure 1 below.

The solute concentration in the fluid is modeled on the fluid phase $D^\delta$ by the following nonlinear stochastic diffusion equation with initial and boundary conditions, where the stochastic term captures external random fluctuations:

where $T \in(0, \infty)$, $u^\delta$ represents the solute concentration in the fluid, $u^\delta_{0}$ represents the starting solute concentration in the fluid phase, $\nu$ is the exterior unit normal to $D^\delta$, $\kappa>0$ is the diffusion coefficient, $f^\delta_{1}$ is a nonlinear function representing an external source of energy that depends on the solute concentration in the fluid phase and its diffusion, $f^{\delta}_{2}$ is a nonlinear function representing interchanges of chemical flow across the surface of the skeleton $\Gamma^{\delta}$. As in the deterministic case, see ^[11]. The solute concentration on the surface of the skeleton is represented by $v^\delta$, $\gamma>0$ is the adsorption factor and $g^\delta_{1}W_{1}$ is an external nonlinear random fluctuation affecting the concentration of the solute in the fluid phase with $g^\delta_{1}$ representing the intensity of the noise and $W_{1}$ an $m$-dimensional Brownian motion defined on a complete $(\Omega, \mathcal{F}, \mathbb{P}, (\mathcal{F}_t)_{0\le t\le T})$ probability space.

On the surface of the skeleton, the concentration of the solute $v^\delta$ is modeled using the following stochastic reaction equation:

where $a>0$ is the reaction factor, $v^\delta_{0}$ is the initial concentration of reactants on the surface of the skeleton, and $g^\delta_{2}dW_{2}$ is an external linear random fluctuation affecting the concentration of the solute on the surface of the skeleton with $g^\delta_{2}$ representing the intensity of the noise and $W_{2}$ defined on the same probability space as above. Let us note that the boundary condition $-\kappa \frac{\partial u^\delta}{\partial \nu} = \delta\gamma(h(t, u^{\delta})-v^\delta), \text{ in }\Omega \times \Gamma^\delta \times (0, T)$ is meant to couple the nonlinear stochastic diffusion system (1.1) in the fluid phase $D^\delta$ and the reaction stochastic system (1.2) in the skeleton.

The rest of this paper is organized as follows: In Section 2, we introduce several assumptions to define a solution for the coupled stochastic partial differential equations. In Section 3, we establish Theorem 2.1 and derive a mild-weak probabilistic solution for the system (1.1)-(1.2). This is followed by a path-wise uniqueness result in Section 4, which establishes a strong probabilistic solution. In Section 5, we show that, given additional data assumptions, the solute concentration in the fluid phase and the reactant concentration on the skeleton's surface remain positive. We conclude this work with Section 6, where we present numerical results. In this section, we illustrate smooth Langmuir and Freundlich kinetics, employing extended stochastic non-conforming finite element methods for discretizing the coupled SPDE. Additionally, we numerically, analyze the convergence order of this method.

2.   Assumptions and definition of a solution

The general probabilistic functional spaces, which we will frequently employ in this paper, will now be introduced. Let $\mathcal{B}$ be a Banach space, and $p, q \in [1, \infty]$. The space $L^{p}(0, T;\mathcal{B})$ is defined to be the set of all measurable functions

such that $\lVert \phi(t) \rVert_{\mathcal{B}}$ is $p$ integrable in the set $[0, T]$. The space $L^{p, q}\left(\Omega; (0, T);\mathcal{B})\right)$ is the set of all of functions $v : (\omega, t) \in \Omega \times [0, T] \longrightarrow v(\omega, t, \cdot)\in \mathcal{B}$, where $v(\omega, t, x)$ is $\mathcal{F}_{t}$-measurable in $\omega$ for all $t$. This space can be equipped with the following norm:

For more general properties of these functional spaces, we refer to ^[9,18,20,21]. In the following, we provide the necessary assumptions on the data of our problem.

Assumptions:

(A1) The initial condition $(u^{\delta}_{0}, v^{\delta}_{0})$ are uniformly bounded in $L^{2}(D^{\delta})\times L^{2}(\Gamma^{\delta})$.

(A2) $f^{\delta}_{1}(t, u^\delta, \nabla u^{\delta}) = F^{\delta}_{1}(t, u^{\delta})\cdot \nabla u^{\delta}$ such that

(ⅰ) $F^{\delta}_{1} = (F^{\delta}_{1, 1}, F^{\delta}_{1, 2}, \ldots, F^{\delta}_{1, n})$, where $F^{\delta}_{1, i}(\cdot, v)\in L^{2, 2}(\Omega; (0, T);L^{2}(D^{\delta}))$ for all $v \in L^{2, 2}(\Omega; (0, T);L^{2}(D^{\delta}))$ and $F^{\delta}_{1, i}$ satisfies Lipschitz condition with respect to the second argument in the $L^2$-norm;

(ⅱ) $\left(f^{\delta}_{1}(t, u^\delta, \nabla u^{\delta}), \phi\right)_{L^{2}(D^{\delta})}\leq C\|\nabla u^{\delta}\|_{L^{2}(D^{\delta})}\|\phi\|_{L^{2}(D^{\delta})}$.

(A3) $g^{\delta}_{1} = (g^{\delta}_{1, 1}, g^{\delta}_{1, 2}, \ldots, g^{\delta}_{1, m})$ such that $g^{\delta}_{1, i}(\cdot, v)$ satisfies Lipschitz condition with respect to the second argument in the $L^2$-norm and the following linear growth:

(A4) The interchanges of chemical flows across the boundary are given by the nonlinear function $h:\Omega\times(0, T)\times \mathbb{R}\rightarrow \mathbb{R}$ satisfying

(ⅰ) $h(\cdot, 0) = 0$ and $h$ is monotonously non-decreasing function,

(ⅱ) $h$ is continuously differentiable with respect to the second argument,

(ⅲ) $|\frac{\partial h}{\partial z}(\cdot, z)|\leq C(1+|z|^{p-1})$ for all $z\in \mathbb{R}$, $C>0$, and

(A5) $g^{\delta}_{1} \in L^{2}(0, T;L^{2}(D^{\delta}))$.

Remark 2.1. Note that, from Assumption (A4(i)) and (A4(ii)), one can deduces the following:

● $zh(z)\geq 0$,

● $|h(z)| \leq C(1+|z|^{p})$, for all $z\in \mathbb{R}$.

We now, introduce the notion of a weak probabilistic solution to our model. The notion of a weak probabilistic solution to our model is now introduced.

Definition 2.1. The system $(\Omega, \mathcal{F}, \mathbb{P}, u^{\delta}, v^{\delta}, W_1, W_2)$ is said to be a weak probabilistic solution to the model (1.1)-(1.2), if:

(a) $W_1$ and $W_2$ are $\mathcal{F}_{t}$-Wiener processes ($m$-dimensional), where $\mathcal{F}_{t}$ is a filtration defined on $(\Omega, \mathcal{F}, \mathbb{P})$.

(b) The mappings $(\omega, t) \rightarrow u^{\delta}(\omega, t)$ and $(\omega, t) \rightarrow v^{\delta}(\omega, t)$ are progressively measurable.

(c) $(u^\delta, v^\delta)$ satisfy, for $\sigma(dx)$ a surface measure on the boundary $\Gamma^{\delta}$

for all $0\leq t \leq T$ and $\psi \in \mathcal{V}_\delta$ where $\mathcal{V}_\delta = \{\phi \in H^{1}(D^{\delta})\ | \ \phi = 0\, \text{ on }\, \partial D^{\delta}\}$, and

Definition 2.2. Let $(\Omega, \mathcal{F}, \mathbb{P}, u^{\delta}_{1}, v^{\delta}_{1}, W_1, W_2)$ and $(\Omega, \mathcal{F}, \mathbb{P}, u^{\delta}_{2}, v^{\delta}_{2}, W_1, W_2)$ be two probabilistic weak solutions of system (1.1)-(1.2) with the same initial condition $(u^{\delta}_{0}, v^{\delta}_{0})$, we say that (1.1)-(1.2) admits path-wise uniqueness if

Then, we have the following result.

Theorem 2.1. Suppose that the Assumptions (A1)–(A4) hold true. Then for fixed $\delta$ and for all positive real number $T$, there exists a weak probabilistic solution $(\Omega, \mathcal{F}, \mathbb{P}, u^{\delta}, v^{\delta}, W_1, W_2)$ of system (1.1)-(1.2) by means of Definition 2.1.

Theorem 2.2. Let (A1)–(A4) hold, then the system (1.1)-(1.2) has the path-wise uniqueness property in the sense of Definition 2.2.

3.   Existence results

In this section, we establish the existence of a weak probabilistic solution employing the Galerkin approximation method, Prokhorov tightness property, and Skorokhod representation theorem.

3.1.   Galerkin's approximate solution

Using the Galerkin approximation method, we demonstrate the existence of solutions. Let $(\ell_{k}^{\delta})_{k = 1}^{\infty}\subset [\mathcal{V}_\delta \cap L^{\infty}(D^\delta)]$ be sequence of linearly independent vectors and consider $H_n = \mathrm{span}\{\ell_{k}^{\delta}, \ k = 1, 2, \ldots, n\}$ to be dense subset of $\mathcal{V}_\delta$ and define the projection $\mathcal{P}_n:L^2(D^\delta)\rightarrow H_n$. We now let

where $\varphi^{\delta}$ in $L^2(\Omega; C([0, T];L^2(\Gamma^\delta)))$, we seek an approximate vector solution to our problem in finite dimensions as

we demand that $u^{\delta}_{n}$ and $\rho^{\delta}_{n}$ meet the following system:

and

where

The corresponding system of stochastic ODEs satisfied by the Fourier coefficients $c^{i}_{n}$ and $d^{i}_{n}$ has a unique solution. This gives the existence of $u^{\delta}_{n}$ and $\rho^{\delta}_{n}$ that solve the system (3.2)-(3.3).

3.2.   Energy and finite difference estimates

In this subsection, we derive crucial a priori estimates that will be of great importance when studying the asymptotic behaviour of the solutions of the considered model. For the proof of the following lemma, we refer to ^[10].

For notational simplification we shall use $u^{\delta}_{n}(t)$ to denote $u^{\delta}_{n}(t, \cdot)$ and $\rho^{\delta}_{n}(t)$ to denote $\rho^{\delta}_{n}(t, \cdot)$.

Lemma 3.1. For $D^{\delta}$ and $S^{\delta}$ as constructed above, we have

where $\alpha >0$, for all $w \in \mathcal{W}_{\delta}^{1, 2}$, where $\mathcal{W}_{\delta}^{1, 2} = \left\{\phi \in \mathcal{W}^{1, 2}(D^\delta)\ |\ \phi = 0\ \mathit{\text{on}}\ \partial D^\delta \right\}.$

Theorem 3.1. The constructed approximation $u^{\delta}_{n}$ satisfies the following estimates:

for some positive constant $C$.

Proof. We first note that the solution of (3.3) is given by

from which one obtains

We apply Itô's formula to the integral equation (3.2) using the function $\phi(u^{\delta}_{n}(t)) = |u^{\delta}_{n}(t)|^{2}_{L^2(D^{\delta})}$, to get

Using Cauchy-Schwartz's inequality flowed by Young's inequality and the assumptions on the nonlinear term $h(u^{\delta}_{n})$, we obtain

Integrating over the interval $(0, t)$, taking the supremum and the expectation to both sides of (3.9), we get

Using the bound (3.7), Remark 2.1, Assumptions (A1) and (A5), and Lemma 3.1, we obtain

However, we have from (A2(ⅱ)) and Young's inequality

for any $\lambda>0.$ Also from (A3), one sees that

Regarding the stochastic term in (3.11) we use Burkholder-Davis-Gundy's and Young inequalities as follows:

for any $\eta>0$. From (3.11)–(3.14) and Gronwall's inequality we have

We can achieve only weak limits for sub-sequences of the Galerkin approximate solution of our problem using the above estimates. Strong convergence requires some compactness, but because we are dealing with stochastic processes, bounds on the time derivative of the solution cannot be obtained. We have the following bounds for the finite difference of $u^{\delta}_{n}$.

Theorem 3.2. Let $u^{\delta}_{n}$ be the approximate solution of problem (1.1). Then under Assumptions (A1)–(A5) there exists a positive constant $C$, independent of $\delta$, such that for all $\rho \leq 1$ and all $s$ with $t+s \in [0, T]$, we have

Proof. For any $s>0$, the solution of problem $(P^{\delta}_{1})$ satisfies

from this we obtain

Let us estimates the terms on the right hand side of (3.16) as follows:

Next, from the Cauchy-Schwartz inequality, we have

Using Lemma 3.1, Eqs (3.4) and (3.7), we obtain

We also have from the embedding of $L^{2}(D^{\delta})$ into $W^{-1, 2}(D^{\delta})$, Assumption (A2(ⅱ)) and Cauchy inequality that

Once again, we use the embedding of $L^2(D^{\delta})$ into $W^{-1, 2}(D^{\delta})$, followed by Itô's isometry, Cauchy-Schwartz inequality, and Fubini's theorem that

From estimates (3.5), the assumptions on $f_{1}^{\delta}$ and $g_{1}^{\delta}$ (3.16)–(3.20), the proof is complete.

3.3.   Probabilistic compactness

As stated earlier, the goal is to take $n$ goes to infinity in ($u^{\delta}_{n}$, $\rho^{\delta}_{n}$) in order to arrive at ($u^{\delta}$, $\rho^{\delta}$) a solution of the system (2.1)-(2.1). The estimates (3.5) aid in the extraction of convergent sub-sequences from ($u^{\delta}$, $\rho^{\delta}$). However, the presence of the nonlinear function $h$ in (2.1) necessitates strong compactness for $u^{\delta}_{n}$. Theorem 3.2, together with the estimates (3.5), we make sense of the set

Following Bensoussan ^[3] (and ^[19,24]), it is easily seen that $\mathbb{Z}_{\delta, n}$ is compactly embedded in $L^{2, 2}(\Omega; (0, T);L^{2}(D^{\delta}))$. Having this, we define the set

and the mapping

On the Borel set $\mathcal{B}(\mathcal{I})$ of the set $\mathcal{I}$ we define a probability measure as pullback of the mapping $\Phi_{n}$ as follows:

Again, following Bensoussan ^[3] (see also Sango ^[24] and Mohammed and Sango ^[19]), we show that the family $\{\mu_n\}$ is tight. From Prokhorov's compactness results ^[5], we obtain a subsequence $\{\mu_{n_\nu}\}$ of $\{\mu_n\}$ and a probability measure $\mu$ such that $\mu_{n_\nu}$ converging weakly to $\mu$. As a consequence, by Skorokhod's compactness theorem ^[5], we are able to construct a new probability space $(\Omega_1; \mathbb{F}_1;\mathbb{P}_1)$, set of random variables $\{(u^{\delta}_{n_\nu}, W^{n_\nu})\in \mathcal{B}(\mathcal{I}):\, n_\nu \in \mathbb{N}\}$ and $(u^{\delta}, W)$ such that the probability law of $(u^{\delta}_{n_\nu}, W^{n_\nu})$ is $\mu_{n_\nu}$ and the law of $(u^{\delta}, W)$ is $\mu$. In addition to that we have

In the following lemma, we transform our problem to a new setting in which the sequence of solutions has nicer properties and, more precisely, has a strong convergence in probability.

Lemma 3.2. Define on the probability space$(\Omega_1; \mathbb{F}_1;\mathbb{P}_1)$ the filtration $\mathbb{F}_{1t} = \sigma(\{u^{\delta}(s), W_s\}_{s \in [0, t]})$. Then

● $W$ is an $(\mathbb{F}_{1t})_{t\geq 0}$ Brownian motion;

● $(u^{\delta}_{n_\nu}, W^{n_\nu})$ satisfies with probability $1$,

and

where

3.4.   Passing to the limit

Before we proceed to the passage to the limit, we should note that nonlinearities pose a significant challenge in this regard. As for the nonlinear operator $h$ that represents the interchanges of chemical flows across the boundary, Bituin and Donato ^[6] have examined a number of its properties in the elliptic framework. In the following lemma, we give the evaluation version of its major properties (see [6,Theorem 3.2,p. 179]).

Lemma 3.3. Let $h$ be as in (A4) and $s$ and its conjugate $s'$, i.e., ($\frac{1}{s}+\frac{1}{s'} = 1$), are such that

Then, the application

is weakly continuous, i.e., for all bounded sequence $\{v_n\}$ in $L^2(0, T;\mathcal{W}^{1, 2}(D^\delta))$, one has up to a sub-sequence

Note that, estimates (3.5) still true for the variational form (3.22), which gives the $\mathbb{P}_1$–a.s. weak$^*$ and weak convergence

The limits (3.26) and (3.27) allow us to pass to the limit in the first two terms on the left-hand side of (3.22). In order to pass to the limit in the third term on the left-hand side of (3.22), we use the weak convergence (3.25) and obtain

Regarding the initial condition, it is known that the projection $\mathcal{P}_{n_\nu} u^{\delta}_{0}$ converges strongly to $u^{\delta}_{0}$ in the $L^2$-norm. We also have

this together with (3.25) give

this gives the corresponding limit of the second term on the right-hand side of (3.22). It also gives

For the third term on the right-hand side of (3.22), we have

The first term on the right-hand side of (3.31), will converge to zero due to the assumption (A2(ⅰ)) and the strong convergence (3.21). Then, we pass to the limit on the second term using the weak limit (3.27), we obtain

Now, let us show that

for this, we write

Because the variation $\left(W^{n_\nu}(s)-W(s)\right)$ is unbounded, the passage to the limit on the first term of the right-hand side of (3.34) requires special attention, so for one to benefit from the strong $\mathbb{P}_1\text{–a.s.}$ convergence (3.21). We utilize the concept of regularization

where the function $\psi$ is the standard mollifier. By definition, we have

also, $g^{\delta, \eta}_{1}$ is bounded by $g^{\delta}_{1}$ and differentiable in time. We write

We deal with the right-hand-side as follows: For the first term we use Burkholder-Davis-Gundy's inequality and the strong convergence (3.35),

Clearly, the last term converges to zero $\mathbb{P}$–a.s as $\eta$ tends towards $0$.

Integration by parts, assumptions on the nonlinear function $(g_{1}^{\delta}(t, u^{\delta}_{n_{\nu}}(t))$, and the strong convergence (3.21) lead to

The right hand side of (3.38) tends towards $0$ $\mathbb{P}$–a.s. as $n_{\nu }$ tends to $\infty$.

Using (3.37) and (3.38) into (3.34), we arrive at

However,

We use Rozovskii's convergence theorem for stochastic integrals [23,Theorem 4, p. 63] to assert the following:

Combining the above convergence, we obtain

and

where

This concludes the demonstration that $(\Omega, \mathbb{P}, \mathcal{F}, u^{\delta}, v^{\delta})$ is a weak probabilistic solution to the system (1.1)-(1.2).

4.   Uniqueness

In this part, we prove the path-wise uniqueness of the solution of problem (1.1). We assume that $u^{\delta}_{1}$ and $u^{\delta}_{2}$ solve the system (3.42)–(3.44) and let $w^{\delta} = u^{\delta}_{1}-u^{\delta}_{2}$. Applying Itô's formula to the function $\phi(w^{\delta}(t)) = \|w^{\delta}(t)\|^{2}_{L^2(D^{\delta})}$, we get

where

and

Integrating (4.1) over $(0, t)$, taking the expectation, the supremum, and using the Assumptions (A4(ⅰ)), we obtain

Now, we shall estimate each of the terms on the right side of (4.4). We start by

We use Assumption (A4) to derive the following:

From (4.5), (4.6) and Lemma 3.1, we arrive at

where $\beta = \frac{2\gamma^2 L}{a+\gamma}$. Second, we use the estimate in Theorem 3.1, Cauchy-Schwartz and Poincaré inequalities and Assumption (A2), we have

where $\lambda>0$ is small enough. Regarding the last two terms on the right-hand side of (4.4), we use Burkholder-Davis-Gundy's, Cauchy-Schwartz, and Young's inequalities and Assumption (A3) to get

Using estimates (4.7)–(4.9) into (4.4), we obtain

choosing $\lambda = \frac{1}{C_1}(\kappa-\frac{\beta \alpha \delta^2}{2})$ and setting $\Lambda = \kappa-\frac{\beta \alpha \delta^2}{2}$, we obtain

It is worth noting that, because $\delta$ represents the hole size, we may always choose it so that $\kappa>\frac{\beta \alpha \delta^2}{2}$. We come to the conclusion that for each $t \in [0, T]$, we have $w^{\delta}(t) = 0$, $\mathbb{P}$–a.s. i.e., $u^{\delta}_{1}(t) = u^{\delta}_{2}(t)$, $\mathbb{P}$–a.s., thanks to the Gronwall's inequality. We also have

This and (4.6) give the uniqueness of the solution of (1.2). As previously stated, in light of the Yamada-Watanabe theorem ^[22], we obtain the existence and uniqueness of a strong probabilistic solution to our model based on the obtained path-wise uniqueness and probabilistic weak solution of the previous section.

5.   Positivity of solutions

The goal of this section is to prove the positivity of the solutions of our system, which can be rewritten as follows:

More precisely, we shall prove under some additional conditions that $u^{\delta}(t, x) \geq 0$ $\mathbb{P}$–a.s. and $v^{\delta}(t, x) \geq 0$ $\mathbb{P}$–a.s. To this end, we apply comparison principles for SPDEs and SDEs. Since the solution $u^{\delta}$ depends only on $v^{\delta}$ via Neumann's boundary condition, it is enough to check the positivity for the separated equations

and

Theorem 5.1. (i) If $u^\delta_{0}\geq 0$ and $f^\delta_1(t, u, \nabla u)\geq 0$ for all $t$ and $u$, then $u^\delta \geq 0$ $\mathbb{P}$–a.s.

(ii) If $v^\delta_{0}\geq 0$ and $\gamma(h(t, u)-v) \geq av$ for all $t$ and $u, v$, then $v^\delta \geq 0$ $\mathbb{P}$–a.s.

Proof. For (ⅰ), according to the result of Denis et al. [12, Theorem 5, p. 518], it follows that if the initial condition $u^\delta_{0}$ and the drift coefficient $f^\delta_1(t, u, v)$ are non-negative, then the solution of the SPDE (5.1) is also non-negative.

Similarly, for (ⅱ), we apply the comparison principle for SDEs and refer to ^[14] for more details on related results. Hence, if the initial condition $v^\delta_{0}$ and the drift coefficient $\gamma(h(t, u)-v) - av$ are non-negative, then the solution of the SDE (5.2) is also non-negative.

6.   Numerical experiments

This section deals with numerical experiments to illustrate and support the above theoretical results. To perform these numerical experiments, we consider the coupled stochastic partial differential system (1.1)-(1.2) with Neumann boundary conditions and initial conditions on the perforated domain $D = (0, 1)\times (0, 1)$ with $D^\delta = D \setminus \bigcup_{i = 1}^4 \Gamma^\delta_i$ and $\Gamma^\delta_i = \{(x_i, y_i) \in \mathbb{R}^2; (x - x_i)^2 + (y - y_i)^2 \leq 0.042\}$, where $x_i, y_i \in \{1/8, 1/4, 3/8, 1/2, 5/8, 6/8\}$, see Figure 2.

In order to discretize the preceding system in time, we partition the interval $I = (0, T)$ into $M$ subintervals $I_n = (t_{n-1}, t_n]$, where $t_0 = 0 < t_1 < \ldots < t_N = T$. We set the time length of each step as $\Delta t : = t_n-t_{n-1}$. The main idea behind variational time discretization is that we approximate the solution $v$ defined in $I$ via a piecewise polynomial function with unstructured mesh. For the stochastic terms $g^\delta_{1}(t, u^\delta) \frac{\partial W_1}{\partial t}$ and $g^\delta_{2}(t, u^\delta) \frac{\partial W_2}{\partial t}$, we use the Euler-Maruyama method. All the numerical experiments are developed in FEniCSx Project and performed with Python on an Intel Xeon (4-core) with 3.60 GHz and 16 GB RAM. The DOLFINx version utilized was 0.5.0. The analysis for nonconforming function spaces was carried out with both the direct and Krylov solvers. This transient analysis solves the variational problems $T = 2$ times, resulting in a substantially larger analysis to run than the steady-state analysis. As a result, the execution time of this program is significantly longer than that of the steady-state program. The discrete problem with Neumann and Boundary conditions is addressed in a For loop from $t = 0$ to $t = T$ with the time step $\Delta t$. Thus, the discrete problem is solved at each time step, and the result is saved in an XDMF file within the loop.

To fix the ideas, we choose in all experiments $\gamma = 0.35$, $a = 0.25$, $\vartheta = 0.5$, $\kappa = 2$, $\delta = 7$ and the diffusion coefficient $\kappa = 0.035$ (but any other combination of coefficients would serve our purposes), and the initial conditions are given by $(u^{\delta}_{0}, v^{\delta}_{0}) = (x^{\frac{-1}{4}}, x^{\frac{-1}{4}})\in L^{2}(D^\delta)\times L^{2}(\Gamma^{\delta})$. The nonlinear function $\phi$ describing the interchanges of chemical flow across the surface of the skeleton will be discussed in the two following examples.

6.1.   Test-case 1: smooth Langmuir kinetics

In this test-case, we consider the case where the reaction of the chemical flow on the skeleton surface is modeled by Langmuir kinetics, i.e., we let

where $\phi(u)$ represents the adsorption isotherm in the fluid phase, $\vartheta$ is the adsorption capacity, and $\kappa$ is the isotherm Langmuir constant (see ^{[6,7,8,10,11]}), and we let $u\neq \frac{-1}{\kappa}, \text{for all} (t, x)\in (0, T)\times D^{\delta}$. With this setting, if $u^{\delta}\geq 0$ in $D^{\delta}$, it is clear that the Assumption (A4) is met by Langmuir kinetics and as a result, we have that $(u^{\delta}, v^{\delta})$ satisfies

for all $0\leq t \leq T$ and $\psi \in \mathcal{V}_\delta$ and

and Theorems 2.1 and 2.2 hold true.

6.1.1.   Evolution plots for deterministic and stochastic cases

The deterministic solute concentration represents the average behavior of the system under fixed parameters, providing a reliable baseline for comparison. In contrast, the stochastic solute concentration accounts for the inherent randomness and variability present in the system, capturing a more comprehensive view of the possible fluctuations in concentration levels due to uncertainties in the parameters or external influences. This dual analysis allows us to better understand the solute behavior under different scenarios and is critical for validating the effectiveness of the numerical methods employed.

In the Figure 3 below, the solution was computed using a non-conforming finite element method with a spatial mesh size of $h$ and a time step size of $\Delta t$. This approach enables the analysis of both deterministic and stochastic solute concentrations within the considered model. We can observe that all oscillations are strongly distributed and extend far from the skeleton's surface due to the use of Langmuir kinetics functions and the associated parameters. This explains the absence of significant disturbances at the skeleton level.

6.1.2.   Mean-square error and convergence orders

To analyze the quality of our numerical approximations, we look at an estimate of a strong mean-square error in $L^2$ -norm, for spatial mesh-size $h$ and temporal mesh-size $\Delta t$, by computing the following formula:

where $u_h$ represents a finite element approximation of $u$ within the finite element space $V_h$, and this approximation can be expressed in terms of the finite element basis $\{\psi^i_n\}_{i = 1}^N$ of $V_h$ and for each time $t_n$ :

Since an exact solution for stochastic partial differential equation $u$ cannot easily be found, we must instead use a numerical solution for partial differential equation within $g_1 = g_2 = 0$. This approximation is chosen to be the finite element solution of PDE in a deterministic case, denoted by $u^{deter}_h$, solved in refined uniform mesh (see Figure 2) with a total of $N = 2^{11}+1$ vertices and mesh-size $h_{ref} = 2^{-11}$. We now estimate the strong error for $u_h^{stoch}$ on the mesh sizes $h = 2^{-k}, \, k\in\{1, 2, 3, \ldots, 10\}$ with the refined solutions solved on a grid with mesh-size $h_{ref}$ and time mesh $\Delta t \in \{10^{-2}; 5.10^{-2}; 2, 5.10^{-3}; 1, 25.10^{-3}; 6, 25.10^{-4} \}$.

In Table 1, we present the computed errors for the solute concentration in the fluid in energy and $L^2$ norms and the solute concentration on the surface of the skeleton in $L^2$ norm, on a sequence of uniformly refined meshes for space, as well as the convergence order computed from the errors on two successively refined meshes (with $N$ and $4N$ elements). Similarly, in Table 2 we present the computed errors for accuracy time. The convergent rate in both time and space is assessed by means of mean-square approximation errors at the endpoint $T = 0.2$, which are induced by both temporal and spatial discretizations. The anticipated amount of error is approximated by taking the mean of $500$ samples for every efficiency test.

Utilizing the theoretical findings, we numerically obtain the optimal convergence rates concerning spatial discretization and validate the theoretical results for the spatial mesh size

and for time-mesh $\Delta t$,

6.2.   Test-case 2: non-smooth Freundlich kinetics

Another well-known example is Freundlich kinetics, where we allow the chemical reaction to proceed on the skeleton surface with the formula

where $\lambda$ is called the reaction order. It is seen that this function is not smooth, although $\phi(t, 0) = 0$, $\phi(t, u)$ is defined for all values $u(t, x) \in \mathbb{R}$ and continuous and $|\phi(t, u)|\leq C(1+|u|))$ for some constant $C>0$. One of this function's key properties, as stated in ^[11], is the existence of a convex and lower semi-continuous function $\Phi :(0, T)\times\mathbb{R}\rightarrow \mathbb{R}$, such that

To study the existence and uniqueness in this case, one could approximate the system (1.1)-(1.2), using Yosida regularization, so for $\eta >0$, we have

for all $0\leq t \leq T$ and $\psi \in \mathcal{V}_\delta$ and

where

Now, the function $\phi^{\eta}(t, u^{\delta, \eta})$ can be smoothed out with the standard mollifier, and the existence and uniqueness results for the system (1.1)-(1.2) can be easily obtained.

6.2.1.   Evolution plots for deterministic and stochastic cases

Similarly to the previous numerical example, in the Figure 4 below, the solution was computed using a non-conforming finite element method with a spatial mesh size of $h$ and a time step size of $\Delta t$. This approach enables the analysis of both deterministic and stochastic solute concentrations within the considered model. Unlike the previous example, all oscillations are sparsely distributed and have a small size, but they extend widely around the skeleton's surface due to the shape of the Freundlich kinetics function and the associated parameter $\lambda \in (0, 1)$. This explains the presence of significant disturbances at the skeleton level.

6.2.2.   Mean-square error and convergence orders

To illustrate the structure of the solute concentration $u$ in dependence on the mesh size of the perforated domain, we include samples next to the convergence plots by using the previous formula (6.5). In this case, we consider the numerical solute concentration obtained by the finite element solution of PDE as an exact solution, denoted by $u^{deter}_h$ which is solved in refined uniform mesh (see Figure 2) with a total of $N = 2^{11}+1$ vertices and spatial mesh $h = 2^{-11}$ and time mesh $\Delta t = 10^{-6}$. Similarly to the previous test case, we estimate the strong error for $u_h^{deter}$ on the mesh sizes $h = 2^{-k}, \, k\in\{1, 2, 3, \cdots, 10\}$ with the refined solutions solved on a grid with mesh-size $h_{ref}$ and time mesh $\Delta t \in \{10^{-2}; 5.10^{-2}; 2, 5.10^{-3}; 1, 25.10^{-3}; 6, 25.10^{-4} \}$.

In Tables 3 and 4, we present the computed errors for the solute concentration in the fluid in energy and $L^2$ -norms and the solute concentration on the surface of the skeleton in $L^2$-norm on a sequence of uniformly refined meshes for space and time, as well as the convergence order computed from the errors on two successively refined meshes. The convergent rate in both time and space is assessed by means of mean-square approximation errors at the endpoint $T = 0.2$, produced by both temporal and spatial discretizations, and $\lambda = 1/2$. The anticipated amount of error is approximated by finding the mean of $500$ samples for every efficiency test.

By analyzing the above results, we numerically retrieve the following optimal convergence orders with respect to spatial and temporal discretization cited in (6.7) and (6.8).

7.   Conclusions

In the present work, we have systematically developed a framework to solve coupled stochastic partial differential equations by introducing key assumptions in Section 2. We established a mild-weak probabilistic solution through Theorem 2.1 in Section 3, and further demonstrated path-wise uniqueness to confirm a strong probabilistic solution in Section 4. Our analysis in Section 5 confirmed the non-negativity of solute and reactant concentrations under specific data conditions. Finally, Section 6 showcased numerical results, demonstrating the efficacy of extended stochastic non-conforming finite element methods for discretizing the coupled SPDE and provided a numerical analysis of the convergence order of these methods, with examples illustrating smooth Langmuir and Freundlich kinetics.

Future research could extend this work by addressing more complex and higher-dimensional systems of coupled stochastic partial differential equations, investigating diverse boundary conditions and noise types, and refining numerical methods for better accuracy and efficiency. Additionally, applying these models to real-world scenarios such as environmental, biological, and financial systems, and integrating machine learning for parameter estimation and predictive modeling, could enhance the practical impact and interdisciplinary relevance of the research.

Authors contributions

M. Eddahbi: Supervision; M. Mohammed: Writing-original draft; M. Eddahbi and M. Mohammed: Conceptualization; M. Eddahbi, M. Mohammed and H. El-Otmany: Formal analysis, Methodology, Validation, Writing-review & editing; M. Eddahbi and H. El-Otmany: Visualization. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The first named author extends his appreciation to the Researchers Supporting Project, Grant number (RSPD2024R1075), King Saud University, Riyadh, Saudi Arabia.

The corresponding author extends the appreciation to the Deanship of Postgraduate Studies and Scientific Research at Majmaah University for funding this research work through the project number (R-2024-1232).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.