Long-time dynamics of a stochastic multimolecule oscillatory reaction model with Poisson jumps

1.   Introduction

Mathematical models which depict dynamics of substrates have played an important role in understanding multimolecule reaction problems. E. E. Sel'kov ^[21] proposed a kinetic model of an open monosubstrate enzyme reaction with substrate inhibition and product activation. Its mechanism can be simplified as

to describe the evolution of reaction concentrations of the two reactants $A_1$ and $A_2$. Here, the concentration of $\bar{A}_0$ is assumed to be constant in time (and space). By the law of mass action and the law of mass conservation, the time evolution of reaction concentrations of $A_1$ and $A_2$ can be described by

where $\bar{x}_0$ is the concentration of $\bar{A}_0$ and $k_i(i = 1, \cdots, 4)$ are kinetic parameters. Herein, all parameters involved in system (1.1) are assumed to be positive constants.

By taking the change of variables

and by rescaling with $\bar{x} = \delta^{(q-1)/p}\beta^{-q/p}X$, $\bar{y} = \delta^{-1}\beta Y$ and $\tau = \delta^{1+(q-1)/p}\beta^{-q/p}t$, system (1.1) can be simplified as

where $a = \alpha\delta^{-1-(q-1)/p}\beta^{q/p}$, $b = \delta^{-1-(q-1)/p}\beta^{1+q/p}$ and $t$ is used to replace $\tau$ in common practice. When parameters $a = 0, \, \, p = n$, and $q = 2$, Zhang ^[27] proved that system (1.2) has a unique positive stable solution and further verified that system (1.1) produced stable limit cycles from Hopf bifurcations as $n < b\ll(3+2\sqrt{2})n$. Furthermore, Tang and Zhang ^[23] verified that system (1.2) occurs Bogdanov-Takens Bifurcation and obtains the corresponding universal unfolding. In addition, there are a lot of works which studied the dynamics of multimolecule oscillatory reactions, a paradigm of non-equilibrium dynamics ^{[9,10,17,22,24]}.

Apparently, the above deterministic description of the chemical reaction model is insufficient since stochastic fluctuations in the concentrations of reactive species are inevitable. Nicolis and Prigogine ^[18] treated the chemical Brusselator as a Markov jump process, namely, the Markov jump Brusselator, which takes the discrete particle structure of the physico-chemical processes involved into account, but lump most of the microscopic information to "internal fluctuations". Thus, they obtained a mesoscopic model in terms of a Markov jump process $(x_t, \; y_t)$ in state space $\mathbb{R}_+^2$, where transition probabilities are described by the so-called master equation (or Kolmogorov's second equation). Interestingly, Nicolis and Prigogine showed that the Markovian process can be simplified as a Poissonian one if the transition events follow an exponential distribution. There have also existed studies on this non-Gaussian noise ^[4,5,13,25]. Besides, Yang et al. ^[26] proposed a reasonable, stochastic multimolecule reaction model driven by the Gaussian noise in the well-stirred case, they further established the criterions of the end of the reaction and continuous reaction conditions. Furthermore, Huang et al. ^[11] studied the permanence of the reaction and estimated the polynomial convergence rate of the transition probability to an invariant probability measure of stochastic system (1.1).

Given that deterministic system (1.1) has an oscillatory behavior, a natural issue is whether oscillations still exist in the stochastic counterpart of this system (i.e., the deterministic multimolecule reaction model is subjected to noise). Owing to the representative of the stochastic multimolecule reaction model, its random attractors are of particular interesting. Meanwhile, Lyapunov exponents play an important role since they can be used to detect the structure of the attractors ^[1,2]. By the stochastic bifurcation theory, Arnold et al. ^[2] investigated Lyapunov exponents of the Brusselator under Gaussian noise and its random attractors and bifurcation behavior using a numerical method. Schenk-Hoppé ^[20] proved the existence of random attractors in the random Duffing-van der Pol system and estimated the corresponding Lyapunov exponents.

In reality, the chemical reactions are usually subject to the same random factors such as temperature, humidity and other extrinsic influences ^[8]. Inspired by this fact, it is more plausible to introduce random perturbations into system (1.1) by replacing the kinetic parameters $k_2$ and $k_4$ by

where $\tilde{N}_q(dt, du)$ denotes a compensated Poisson random measure corresponding to a Poisson measure $N_q(dt, du)$ with characteristic measure $dt\, \nu(du)$ on the product space $[0, \infty)\times U$, and $\nu$ is a finite characteristic measure, i.e., $\nu(U) < \infty$, and further assume that $B_t$ and $N_q(dt, du)$ are independent. Therefore, the following stochastic multimolecule oscillatory system (1.1) with Poisson jumps as $q = 1$ and $p = 2$ is given by

where $x_{t-} = \lim\limits_{s\uparrow t}x_s$.

We point out that the abundant dynamics of the stochastic multimolecule reaction model with the Gaussian noise have been revealed ^[2,6,7]. Meanwhile, note that we considered a stochastic low concentration trimolecular oscillatory chemical system with jumps and established the existence of the corresponded random attractors ^[25], but it is unknown whether random attractors are uniqueness in the stochastic multimolecule oscillatory reaction model with Poisson jumps. Furthermore, if they are unique, what is their structure? The present paper will address these questions and find new dynamical phenomena.

First, we establish the existence-uniqueness theorem of the positive solution of the stochastic multimolecule oscillatory reaction model with Poisson jumps. Then, we derive a sufficient set of conditions that ensure the existence and uniqueness of general random attractors in system (1.3). Moreover, we give the estimation of Lyapunov exponents, and obtain a singleton set random attractor by the estimated Lyapunov exponents. Finally, we introduce some numerical simulations to support the main results.

The rest of this paper is organized as follows. In Section 2, some preliminaries and definitions are formulated. Moreover, the global positive solutions of the stochastic multimolecule oscillatory reaction model with Poisson jumps are established. In Section 3, random attractors and Singleton sets for its stochastic homeomorphism flow are investigated. In Section 4, Numerical simulations are given.

2.   Preliminaries and global positive solutions

In this section, we recall several basic concepts and definitions which will be needed throughout the paper.

Consider the following $d$-dimensional stochastic differential equations with Poisson jumps

with the initial condition $z_0\in\mathbb{R}^d$. Assume that $f\in C^2(\mathbb{R}^d)$, then the infinitesimal generator of the process $z_t$ to (2.1) is

where $\widetilde{C}(z, u) = z+C(z, u)$, $T$ denotes transiposition, and denote $\mathbb{R}^d_+ = \{x\in\mathbb{R}^d:\, x_i > 0, \, i = 1, 2, \cdots, d\}$.

Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a complete probability space. Define the shift operator

it is easy to verify that

and $(t, \omega)\rightarrow \theta_{t}\omega$ is $\mathcal{B}(\mathbb{R})\otimes\mathcal{F}/\mathcal{F}$-measurable. Therefore, $\{\theta_t\}_{t\in\mathbb{R}}$ is a group of measurable transformations of $(\Omega, \mathcal{F}, \mathbb{P})$. Meanwhile, $\mathbb{P}$ is $\{\theta_t\}$-invariant, i.e.,

Let $\{\theta_t\}_{t\in\mathbb{R}}$ be ergodic, then $(\Omega, \mathcal{F}, \mathbb{P}, \{\theta_t\}_{t\in\mathbb{R}})$ is a metric dynamical system.

Definition 2.1. A function $\varphi:\mathbb{R}\times\Omega\times\mathbb{R}^d\rightarrow \mathbb{R}^d$ is called a measurable random dynamical system over the metric dynamical system $(\Omega, \mathcal{F}, \mathbb{P}, \{\theta_t\}_{t\in\mathbb{R}})$, if $\varphi$ is $\mathcal{B}(\mathbb{R})\otimes\mathcal{F} \otimes\mathcal{B}(\mathbb{R}^n)/\mathcal{B}(\mathbb{R}^n)$-measurable and if $\varphi(t, \omega)$ is càdlàg in $t$ and forms a càdlàg cocycle over $\theta_t$, i.e., for any $s, t \in \mathbb{R}$ and $\omega\in\Omega$

Remark 2.1. According to Arnold ^[1], a RDS induces a skew product flow of measurable maps

The flow property $\Theta_{t+s} = \Theta_t\circ\Theta_s$ follows from (2.2).

Definition 2.2. A family random closed set $A(\omega)_{\omega\in\Omega}$ map $\Omega$ into nonempty closed subsets of $\mathbb{R}^d$ such that for any fixed $x\in\mathbb{R}^d$, $\omega\mapsto d(x, A(\omega)): = \inf\{d(x, y)|y\in A(\omega)\}$ is $\mathcal{F}/\mathcal{B}([0, \infty])$-measurable. Here we make the convention $d(x, \emptyset) = \infty$.

Definition 2.3. ^[19] Let $\varphi$ be a càdlàg random dynamical system on $\mathbb{R}^d$ and $\mathcal{D}$ be an IC-system, the set $A\in\mathcal{D}$ is called a random attractor with domain of attraction $\mathcal{D}$ if

$(i)$ $A$ is invariant and compact, i.e., $\varphi(t, \omega)A(\omega) = A(\theta_t\omega)$ for all $t\in\mathbb{R}$;

$(ii)$ $A$ attracts set $C\in\mathcal{D}$, i.e., $\lim\limits_{t\rightarrow \infty}d(\varphi(t, \theta_{-t}\omega)C(\theta_{-t}\omega)|A(\omega)) = 0$, where $d(A|B) = \sup\limits_{x\in A}\inf\limits_{y\in B}d(x, y)$ is the Hausdorff semimetric.

Next, the following theorem shows that the solutions of system (1.3) is positive and global. Throughout this paper, we assume that the coefficient satisfies

Theorem 2.1. Let Assumptions $(H_0)$ and $(H_1)$ hold, then there exists a unique positive solution $(x_t, y_t)$ of system (1.3) for any initial value $(x_0, y_0)\in\mathbb{R}_+^2$, $t\geq0$ and the solution $(x_t, y_t)\in\mathbb{R}_+^2$ almost surely.

Proof. As the drift coefficient of system (1.3) is locally Lipschitz continuous, it follows from Mao ^[15] that there exists a unique local solution $(x_t, y_t)$ for any initial value $(x_0, y_0)\in\mathbb{R}_+^2$ and $t\in[0, \tau_e]$, where $\tau_e$ is the explosion time. Now one shows that $\tau_e = \infty$, a.s. Let $n_0 > 0$ be so sufficiently large that $x_0, y_0$ all lies within the interval $\left[\frac{1}{n_0}, n_0\right]$ which proves the solution is global. For each $n\geq n_0$, define a stopping time

clearly, $\tau_n$ is increasing as $n\uparrow\infty$. Set $\tau_\infty = \lim\limits_{n\rightarrow \infty}\tau_n$, hence $\tau_\infty\leq\tau_e$, a.s. and it is sufficient to check that $\tau_\infty = \infty$. Define a $C^2$-function $V:\; \mathbb{R}_+^2\rightarrow \mathbb{R}_+\cup\{\infty\}$ by

and it is easy to know that $V(x, y)\geq0$ for any $(x, y)\in\mathbb{R}_+^2$. Let $T > 0$ be arbitrary, for any $0 < t < \tau_n\wedge T$ and $(x, y)\in\mathbb{R}_+^2$, applying Itô's formula to system (1.3), one obtains

where

and

For (2.4), one gets

where $I_4 = k_1\bar{x}_0+k_2+k_4+\sigma^2+\int_{U}[\gamma_1(u)+\gamma_2(u)-\log(1+\gamma_1(u))-\log(1+\gamma_2(u))]\nu(du)$ and there is some positive constant $l_2$ such that $I_4\leq l_2$.

For (2.5), one obtains

Moreover, by $(H_0)$ and $(H_1)$, one chooses some positive constant $l_1$ such that the following inequality

hold. Therefore, according to (2.6) and (2.7), there exists a positive constant $l_3$ such that

Integrating (2.3) from $0$ to $\tau_n\wedge T$ and taking expectation on both sides give

Meanwhile, note that

It then follows from (2.9) and (2.10) that

where $I_{\{\tau_n\leq T\}}$ is the indicator function of the set $\{\tau_n\leq T\}$. By the similar proof in ^[16], it gives

Therefore, the stochastic flow $(x_t, y_t)$ of system (1.3) is global to forward, and also implies that $\mathbb{P}\{x_t\geq0, \; y_t\geq0\; for\; any\; t\geq0\} = 1$.

Remark 2.2. Note that $B_t$ has independent increments, $\tilde{N}_q(dt, du)$ is a stationary compensated Poisson random measure, and the coefficients of system (1.3) are independent of $t$, it is easy to know that $(x_t, y_t)$ is a homogeneous Markov process. Moreover, it follows from Arnold ^[1] that system (1.3) can generate a stochastic dynamical system.

Remark 2.3. Define

where $\sharp$ denotes the cardinality of a set. Therefore, the compensated Poisson random measure on $(-\infty, 0]\times U$ can be expressed by

From Qiao ^[19] and Kager ^[12], it follows that $\{q(t), \; t < 0\}$ is a stationary $\{\mathcal{F}_{t}^0\}_{t\leq0}-$adapted Poisson point process with values in $U\backslash\{0\}$. Moreover, it follows from Arnold ^[1] that the solution $z_t$ to system (1.3) is $\mathcal{F}_{t}$-measurable for any $t\in\mathbb{R}$.

3.   Random attractors

In this section, we show mainly the existence and uniqueness of tempered random attractors of system (1.3). First, we state some essential lemma which will be crucial for our analysis in the following content. Consider the following stochastic differential equations

where $c_1(u)$ and $c_2(u)$ be bounded functions with $c_1(u) > -1$.

Lemma 3.1. There exists a $\theta_t$-invariant set $\tilde{\Omega}\in\mathcal{F}$ of $\Omega$ of full $\mathbb{P}$ measure such that for any $\omega\in\tilde{\Omega}$ and $\int_U[\log(1+c_1(u))-c_1(u)]\nu(du) < \frac{1}{2}b_1^2-a_1$,

$(i)$ the random variable $|z(\omega)|$ is tempered.

$(ii)$ the mapping

is a stationary solution of system (3.1) with continuous trajectories and

Proof. $(i)$ By the variation of constant formula ^[4], the solution of system (3.1) is explicitly expressed by

where

Denote

Note that

where $l_5$ and $l_6$ are positive constants.

According to the strong law of large numbers ^[14], one obtains

Since $\lim\limits_{t\rightarrow \infty}\frac{B_t}{t} = 0, \; a.s.$ and $a_1-\frac{1}{2}b_1^2+\int_U[\log(1+c_1(u))-c_1(u)]\nu(du) < 0$, one has the following integrals:

Meanwhile, (3.1) is affine with stable linear part. Thus (3.3) and Arnold ^[1] imply that for any $z_0\in\mathbb{R}$, the unique invariant measure $\mu$ of (3.1) is the Dirac measure supported by

where

Therefore, it follows from Arnold ^[1] that $\lim\limits_{t\rightarrow \infty}\frac{\log^+|z(\theta_t\omega)|}{t} = 0$, $\omega\in\tilde{\Omega}$. That is, the random variable $|z(\omega)|$ is tempered.

$(ii)$ It is easy to see that $H(t, s) = \Phi(t)\Phi^{-1}(s)$, then one has

Besides, denote $s = r+t$, then $H(t, s)$ can be written as

where $\hat{B}_r = B_{r+t}-B_t$ and $\hat{q}_r = q_{r+t}-q_t$.

Therefore,

According to Schenk-Hoppé ^[20], (3.5) and (3.7) imply that $\bar{z}_t(\omega)$ is a measurable stable stationary solution of system (3.1).

Moreover, it follows from Arnold ^[1] that $\bar{z_t}(\omega)$ are continuous trajectories with respect to $(t, \omega)$, $\omega\in\tilde{\Omega}$.

The following theorem is established for the unique tempered random attractor of system (1.3).

Theorem 3.1. If the assumption $(H_0)$ and $(H_1)$ are satisfied. Further assume that for any $u\in U$

and

Then the random dynamical system generated by system (1.3) has the unique tempered random attractor $A(\omega)_{\omega\in\Omega}$ with domain of attraction $\mathcal{D}(A)$ containing the universe of sets $Cl(\mathcal{U})$, generated by

Furthermore, the random attractor $A(\omega)_{\omega\in\Omega}$ of system (1.3) is measurable with respect to $\mathcal{F}_{-\infty}^0 = \sigma\left\{B_t, N_q([t, 0), B);\; t\leq0\right\}$.

Proof. Define $V(x, y) = (x+y)^2$, applying Itô's formula, one obtains

By the comparison theorem ^[5] and ($H_2$), it follows that for any $(x_0, y_0)\in\mathbb{R}^2_+$

where $I_7 = -2\hat{k}+\sigma^2+\int_U[2\check{\gamma}(u)+\check{\gamma}^2(u)-2\hat{\gamma}(u)]\nu(du)$, $I_8 = -2\sigma^2x_sy_s+2k_1(x_s+y_s)\bar{x}_0$ and $I_9(u) = (2+\check{\gamma}(u))\check{\gamma}(u)$.

According to $I_8$, it follows that there exists a positive constant $l_7$ such that $I_8\leq l_7$.

Let $\varphi(t, \omega)(x_0, y_0)$ be the stochastic dynamical systems generated by system (1.3) and $\psi(t, \omega)V(x_0, y_0)$ be generated by the following system

Applying the variation of constant formula to system (3.9), one immediately gets

where

Thus, it follows from (3.8) that the associated stochastic system (3.9) has the following dominating solution $\psi$, i.e.,

By Lemma 3.1 and $(H_3)$, one shows that $\psi(t, \omega)$ has the unique invariant measure $\mu$ supported by

It follows from Lemma 3.1 ($i$) that $z_1(\omega)\geq0$, and it attracts any points with exponential speed. Therefore, it is easy to verify that $\psi(t, \theta_{-t}\omega)z_1(\theta_{-t}\omega)\rightarrow z_1(\omega)$ as $t\rightarrow \infty$ for any $z_1(\omega)$ with $e^{-\epsilon t}z_1(\theta_{-t}\omega)\rightarrow0$, $\epsilon > 0$.

Let $\eta(\cdot):\Omega\rightarrow \mathbb{R}_+$, $\eta(\omega) = \sup\{z|z\in I(\omega)\}$ with $\lim\limits_{t\rightarrow \infty}\frac{\log^+\eta(\theta_t\omega)}{t} = 0$. Define the universe of sets by

From Schenk-Hoppé^[20], there exists a $\epsilon > 0$ such that $e^{-\epsilon t}z(\theta_{-t}\omega)\rightarrow0$ as $t\rightarrow \infty$. Meanwhile, it is clear to see that $\mathcal{U}_1$ is closed under inclusion and $\Omega\times\{z\}\in\mathcal{U}_1$ for any deterministic point $\{z\}\subset\mathbb{R}_+$.

From the definition of $\mathcal{U}_1$ and the above same reference, it follows that the random set $[0, (1+\epsilon)z_1(\omega)]$ is absorbing w.r.t. the universe $\mathcal{U}_1$. Note further that for any $0 < x < y$

According to the proof of Lemma 3.1 $(ii)$, one obtains by (3.10) and (3.12)

that is, the random set $[0, (1+\epsilon)z_1(\omega)]$ is forward invariant for $\psi$ w.r.t. the universe $\mathcal{U}_1$.

Similar to the proof of (3.14), one gets

for any $\epsilon > 0$. Therefore, $[0, (1+\epsilon)z_1(\omega)]\in\mathcal{U}_1$.

Let $B(\omega)$ be a compact set of $\mathbb{R}_+^2$ defined by

It is easy to see that $B(\omega)$ is non-empty and bounded if the pre-images of sets is bounded.

Next, one proves that the family $\{B(\omega)\}_{\omega\in\Omega}$ satisfies the conditions of Schenk-Hoppé ^[20].

In fact, it follows from Schenk-Hoppé ^[20] that $B(\omega)$ is measurability and forward invariant, i.e.,

Moreover, the definition of $\mathcal{U}$ implies that the variable $\eta(\omega) = \sup\{\sqrt{x^2+y^2}:v = (x, y)\in\mathcal{U}\}$ grows sub-exponentially. For any $C\in\mathcal{U}$, note that $V(x, y) = (x+y)^2\leq2|v|^2$, thus one further proves that the random variable satisfies $\sup\{v:\; v\in V(C(\omega))\}\leq2\eta(\omega)$ which grows sub-exponentially, that is, $V(C)\in\mathcal{U}_1$.

Similarly, one gets that there exists a $t(\omega, V(C))$ such that for any $t\geq t(\omega, C)$

Meanwhile, from the fact that $z_1(\theta_{-t}\omega)\leq z_1(\omega)$ and the set $[0, (1+\epsilon)z_1(\omega)]$ absorbing any set in $\mathcal{U}_1$, which implies the absorbtion of any set w.r.t. $\varphi$ in $\mathcal{U}$.

For any $C\in\mathcal{U}$, there exists a random variable $\vartheta(\omega) > 0$ such that $C(\omega)\subset D(\vartheta(\omega)) = \{(x, y)\in\mathbb{R}^2_{+}, \; \sqrt{x^2+y^2}\leq\vartheta(\omega)\}$. It is easy to see that $D(\hat{b}\rho(\omega))\in\mathcal{U}$ and $D(\hat{b}\rho(\omega))$ is a neighborhood of $C(\omega)$ for any $\hat{b} > 1$.

Note that $z_1(\omega)$ is $\mathcal{F}_{-\infty}^0$ measurable, so is $A(\omega)$. Therefore, it gives the complete proof in Schenk-Hoppé ^[20].

Remark 3.1. Compared to Wei ^[25], this paper considers the compensated Poisson random measure and further establishes the unique attractor for the stochastic multimolecule oscillatory reaction model.

Based on Theorem 3.1, the following theorem obtains the singleton sets random attractor of system (1.3).

Theorem 3.2. Let $(H_0)-(H_2)$ hold, if the following assumption

hold, then the random dynamical system generated by system (1.3) has the unique tempered random attractor $A(\omega) = \{(0, 0)\}$ with domain of attraction $\mathcal{D}(A)$ containing the universe of sets $Cl(\mathcal{U})$, which is given by

In particular, for any $(x, y)\in\mathbb{R}^2_+$, the solutions $\varphi(t, \theta_{-t}\omega)(x_0, y_0)$ and $\varphi(t, \omega)(x_0, y_0)$ tend to $\{(0, 0)\}$ with exponential speed as $t\rightarrow \infty$.

Proof. Define a function $V(x, y) = (x+y)^2$. According to the proof of Theorem 3.1, one gets

where $I_7 = -2\hat{k}+\sigma^2+\int_U[2\check{\gamma}(u)+\check{\gamma}^2(u)-2\hat{\gamma}(u)]\nu(du)$, $I_8 = -2\sigma^2x_sy_s+2k_1(x_s+y_s)\bar{x}_0$ and $I_9(u) = (2+\check{\gamma}(u))\check{\gamma}(u)$.

Moreover, denote

then $\mathbb{R}^2_+ = \Omega_1\cup\Omega_2$. For $(x, y)\in\Omega_1$, one has

For $(x, y)\in\Omega_2$, by ($H_4$), it is easy to verify that $I_8\leq0$. Therefore, one further obtains by the comparison theorem for any $(x, y)\in\mathbb{R}^2_+$

According to Lemma 3.1, (3.17), ($H_0$)–($H_2$) and ($H_4$), the top Lyapunov exponent $\lambda_1$ of system (1.3) can be bounded by

From Lemma 3.1, one gets that the stochastic dynamical system generated by the following stochastic system

has the unique invariant measure $\delta_{0}$. Similar to the proof of Theorem 3.1, it shows that $A(\omega) = \{(0, 0)\} = V^{-1}(0, 0)$ is an attractor.

In particular, for any $(x_0, y_0)\in\mathbb{R}^2_+$, the solutions $\varphi(t, \theta_{-t}\omega)(x_0, y_0)$ and $\varphi(t, \omega)(x_0, y_0)$ tend to $A(\omega)$ with exponential speed as $t\rightarrow \infty$.

4.   Examples and computer simulations

In this section, we introduce mainly some examples and numerical simulations to support the main results.

Example 4.1. Let us illustrate the conditions of the unique tempered random attractor for Theorem 3.1. Choosing

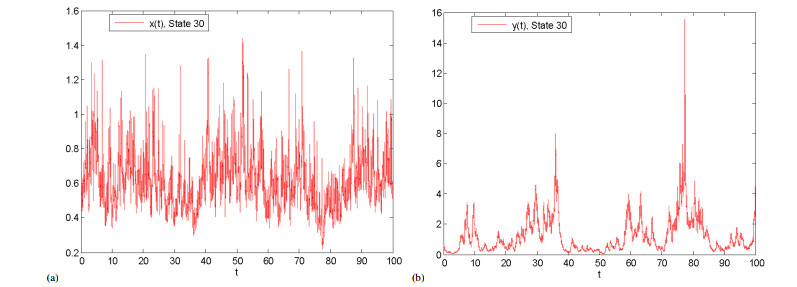
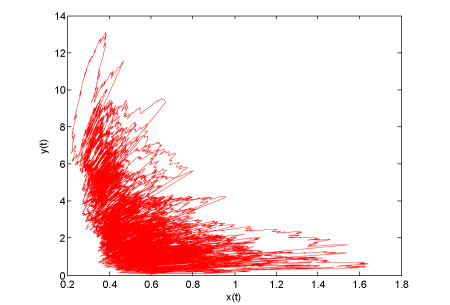
implies that the conditions $(H_0)-(H_3)$ are satisfied. It follows from Theorem 3.1 that system (1.3) has a unique random attractor. Applying the Infinitesimal method ^[28] and ^[3] to simulate (1.3), the simulated of system (1.3) is shown Figure 1. Meanwhile, the numerical simulations of the different samples $x_t$ and $y_t$ are shown as in Figure 2 (a) and (b) .

Example 4.2. Let us illustrate the conditions of the singleton set random attractor for Theorem 3.2. Choosing

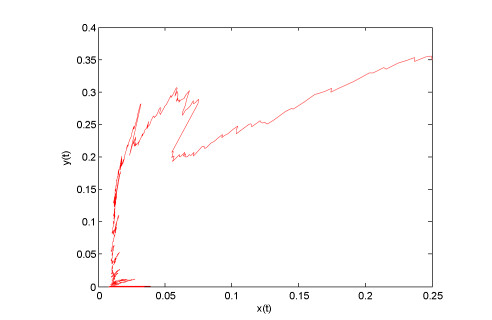
implies that the conditions $(H_0)-(H_2)$ and $(H_4)$ are satisfied. then system (1.3) has a singleton set random attractor by Theorem 3.2. Moreover, the simple simulated orbit of system (1.3) is as shown in Figure 3.

5.   Conclusions

Note that we established the existence of the corresponded random attractors in a stochastic low concentration trimolecular oscillatory chemical system^[25], but the uniqueness is unknown. Based on this fact, we considered a stochastic multimolecule oscillatory reaction model with Poisson jumps in this paper. We have not only obtained that the multimolecule oscillatory reaction model with Poisson jumps has a unique global positive solution, but also importantly obtained the existence and uniqueness of random attractors in the stochastic multimolecule oscillatory reaction model, by using a technique similar to the Lyapunov's direct method.

Acknowledgments

This work is partly supported through the National Natural Science Foundation of China (No.11871118) and National Natural Science Foundation of China (No.11801096).

Conflict of interest

All authors declare no conflicts of interest in this paper.