A cascade dead-zone extended state observer for a class of systems with measurement noise

1.   Introduction

The extended state observer (ESO) proposed by Han Jingqing appeared in 1995. In active disturbance rejection control (ADRC), simultaneous reconstruction of the states of a plant as well as total disturbance using an ESO is one of the most important strategies. Since then, ESO has attracted a lot of research attention because it requires minimal information about the plant and is simple to implement. ESO based controls have been widely applied in various areas involving urban traffic ^[1], motion ^[2], power ^[3], and so on. At first, the classic ESO was only proposed for uncertain systems in series integrator form. The convergence of the classic ESO has been theoretically validated by using various tools like singular perturbation ^[4] and Lyapunov techniques ^[5]. Recently, many studies have been done on ESO design methods for systems that cannot be transformed into series integrators, such as mismatched uncertain systems ^[6], time-delay systems ^[7], multi-coupled subsystems ^[8] and non-minimal phase (NMP) systems ^[9]. In addition, in recent years, some scholars began to pay attention to finite time estimation in order to achieve safety and high steady state accuracy. ^[10] proposed a continuous finite time ESO. The time-varying gain of the observer was designed by defining the time-varying transformation so that the observation error approached zero in finite time. Furthermore, Razmjooei, Palli, Shafiei et al. proposed an adaptive fast finite time ESO to ensure convergence within a short time interval regardless of initial conditions (^[11,12]).

In practical engineering, the measurement noise will be unavoidable. Measurement noise can be amplified by the ESO and entered the outer loop system, which can have adverse effects such as saturation of input actuators, vibration of mechanical systems, and even system instability. Therefore, improving the robustness to measurement noise of the ESO is still an active research topic. In fact, to a large extent, satisfactory system state reconstruction and total disturbance compensation usually result in high gain forms of the ESO (^[5,13]). When the system has a high dimension or a large high gain parameter must be selected to achieve rapid estimation, this high gain leads to some limitations in applications, such as peaking phenomenon, numerical problems and sensitivity to high frequency measurement noise. Therefore, in order to suppress the noise, many strategies have been proposed, mainly the error-based gain-regulation techniques (^[14,15,16]) and the use of cascade structures (^[17,18,19]). On the other hand, combining the ESO with a Kalman filter ^[20] or adding integral terms to the ESO ^[21] are other solutions to attenuate the effects of measurement noise. While the above methods have shown effectiveness in certain control scenarios, they have some limitations, including the introduction of additional system lags, the complexity of tuning methods, and additional design knowledge requirements.

Inspired by Astolfi and Marconi ^[17], ^[18] proposed a new extended state observer with the low power structure (LPESO), which consisted of $n$ second order linear observers. When high frequency noise is present, the LPESO improves the estimation performance by adopting a structure whose gain grows only to the second power. Thus it relaxes the digital implementation requirements. However, linear feedback is used in this low power structure. It can be seen from the numerical simulation in ^[18] that LPESO can reduce the peaking more effectively compared with traditional LESO, but it is still sensitive to persistent high-frequency noise. This is also verified in our numerical simulations.

In this paper, in order to suppress the persistent bounded measurement noise, a total of $n$ observers of second order are designed using dead-zone nonlinear feedback and connected into a cascade structure. The dynamic dead-zone was originally applied to the high gain observer in ^[22], but in this paper, the dead zone nonlinear feedback is designed in the cascade structure, which is a generalization of ^[22]. The dead zone dynamic is composed of two parts. One is to cut down the noise that falls in the zone to improve noise attenuation. The other is to push the dead zone amplitude to converge to $0$ as soon as possible to ensure the convergence of errors. In addition, the cascade structure avoids excessive power increase of the high gain parameter, inherits the good performance of non-amplifying noise, and solves numerical implementation problems. Theoretical analysis shows that LPESO in ^[18] is a linear form of the extended state observer proposed in this paper. By perturbation theory, the convergence of the proposed ESO is proved. Numerical simulations reveal that the cascade ESO with the dynamic dead zone can significantly improve the suppression of persistent bounded measurement noise. Description function method is used to analyze the proposed ESO in the quasi-frequency domain, and the effect of the dead zone nonlinear parameter on the closed-loop system performance is studied. This analysis provides a more intuitive view of its high-frequency noise suppression capability.

This paper is organized as follows. Section 2 formulates a problem for $n$th-order nonlinear system. Section 3 shows input-to-state stability when there is measurement noise. Section 4 provides an example of numerical validation and a quasi-frequency domain analysis is carried out based on Laplace transform and description function. Section 5 offers the conclusion.

Notation. $\mathrm{Diag}^n_{ > 0}$ represents the set of $n\times n$-dimensional diagonal positive definite matrices. $\mathrm{col}(a_1, \cdot\cdot\cdot, a_n)$ denotes a column vector. The Euclidean norm of the vector ${\bf a}$ is defined as $\|{\bf a}\| = \sqrt{{\bf a}^T{\bf a}}$. $\|X\| = (\lambda_{\max}(X^TX))^{\frac{1}{2}}$ represents the $l_2$ norm of the matrix $X$. Given $a\in\mathbb{R}, b\in\mathbb{R}_{\geq 0},$ define $\mathrm{sat}_a(b): = \max\{-a, \min\{b, a\}\}$ and $\mathrm{dz}_a(b): = b-\mathrm{sat}_a(b)$. For a given vector ${\bf c} = [c_1, \cdots, c_n]^T,$ there is $\mathrm{sat}_b({\bf c}): = [\mathrm{sat}_b(c_1), \cdots, \mathrm{sat}_b(c_n)]^T.$

Definition. ^[19] The following system

defined on ${\bf x}\in\mathcal{X}\subset\mathbb{R}^n, {\bf u}_1\in\mathcal{U}_1\subset\mathbb{R}^{m_1},$ ${\bf u}_2\in\mathcal{U}_2\subset\mathbb{R}^{m_2},$ and $t\in[0, +\infty)$ is locally input-to-state stable (ISS) on some bounded sets $\mathcal{X}, \mathcal{U}_1, \mathcal{U}_2$ if there exist a function $\beta$ of class $\mathcal{KL},$ and functions $\gamma_1, \gamma_2$ of class $\mathcal{K},$ such that for any initial condition ${\bf x}(0)\in\mathcal{X}$ and any bounded inputs ${\bf u}_1(t), {\bf u}_2(t),$ solution ${\bf x}(t)$ exists for all $t,$ satisfying

2.   Problem statement

Consider a nonlinear uncertain system of $n$th-order, which can be written in phase-variable form after coordinate changes:

where ${\bf x} = (x_1, x_2, \cdot\cdot\cdot, x_n)^T\in\mathbb{R}^n$ is the state vector, $f(t, {\bf x})$ involves uncertain linear or nonlinear internal dynamics, $y\in\mathbb{R}$ is the measured output, $u\in\mathbb{R}$ is a control signal, $d^*\in\mathbb{R}$ is the unknown external disturbance and $v$ represents an unknown measurement noise. Define

as the total disturbance. We are interested in designing the ESO to simultaneously estimate the state vector as well as the total disturbance despite the measurement noise $v(t)$.

Assumption 1. For all ${\bf x}\in D$ and $t > 0$, the total disturbance $d(t, {\bf x})$ is bounded by $|d(t, {\bf x})|\leq m_d,$ and the bound of its derivative is $m_{\dot d},$ i.e., $\left| \frac{\mathrm{d}}{\mathrm{d}t} d(t, {\bf x})\right|\leq m_{\dot d}.$

Assumption 2. Measurement noise $v(t)$ is bounded, that is $|v(t)|\leq m_v.$

In order to estimate the states and total disturbance of system (2.1), the order of the traditional ESO is $n+1$. Therefore, when the plant order is large, the high gain parameter of the ESO will grow to a power of $n+1$, resulting in the amplification of measurement noise and pollution of the estimates. To solve this problem, inspired by ^{[17,18,22,23]}, we design an observer with dynamic dead-zone in a cascade structure for persistent bounded high frequency noise that affects the measurement output. This is a structure consisting of a cascade of $n$ second-order observers with dynamic dead zone feedback. For $i\leq n-1$, if $x_i$ and $x_{i+2}$ are known, design second-order dynamic dead zone observers for $x_i$ and $x_{i+1}$ as follows

where $\hat x_i$ and $\eta_i$ are the estimations of $x_i$ and $x_{i+1}$, $l$ is the high gain parameter, $k_{i1}$ and $k_{i2}$ are parameters to be designed. $\sqrt{\sigma_i}$ is the threshold, satisfying the following dynamic system

In the above system, $\lambda > 0$ is a constant, $w$ is the parameter to be designed. Similarly, second-order dynamic dead zone observer of $x_n$ and $d(t, {\bf x})$ takes the form as

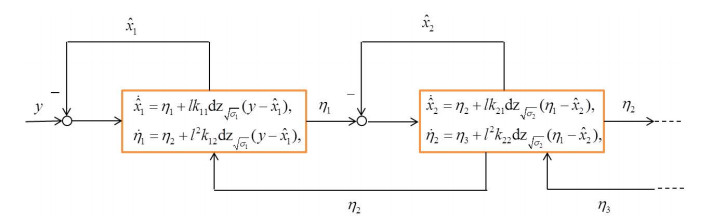
in which $l, k_{n1}, k_{n2}, \lambda$ and $w$ are defined as above. In fact, we take the total disturbance $d(t, {\bf x})$ as an extended state of system (2.1). If $x_n$ is known, (2.4) is an extended state observer for $x_n$ and $d(t, {\bf x})$, $\hat x_n$ and $\eta_n$ are estimations, respectively. However, only $x_1$ is measurable, and $x_2, x_3, \cdots, x_n$ are unknown state variables in system (2.1). Thus, we replace $x_i$ and $x_{i+2}$ with the second state $\eta_{i-1}$ and $\eta_{i+1}$ in the $(i-1)$the observer and the $(i+1)$th observer, respectively. Meanwhile, $x_n$ is replaced by the second state $\eta_{n-1}$ in the $(n-1)$th observer. Then the above $n$ second-order observers (2.2)–(2.4) are connected into a dynamic dead zone observer with a cascaded structure (Figure 1).

As can be seen from Figure 1, a total of $n$ dead-zone dynamics are needed for $n$ output injection channels. To simplify the design, we define the same dead-zone amplitude determined by the sum of the squares of output injection terms. Thus, an extended state observer with dynamic "dead-zonated" output injection (DZ-CESO) is introduced to deal with persistent bounded measurement noise affecting the measurement output, as shown below

where $z_i = (\hat x_i, \eta_i)^T\in\mathbb{R}^2, {\bf z} = (z_1, \cdot\cdot\cdot, z_n)^T$ denotes a state of the proposed DZ-CESO. In (2.5),

$B = (0, 1)^T, C = (1, 0)$, $D(l) = \mathrm{diag}(l, l^2)\in\mathrm{Diag}^2_{ > 0}$. The parameters $K_i = (k_{i1}, k_{i2}) (i = 1, \cdot\cdot\cdot, n)$ are designed later. Define two block diagonal matrices in $\mathbb{R}^{n\times 2n}$,

From the above analysis we can see that $\hat{{\bf x}} = L_1{\bf z}$ can be seen as a correction for $\hat{{\bf x}}' = L_2{\bf z}$. Then we take $\hat{{\bf x}} = L_1{\bf z}$ and $\eta_n = B^Tz_n$ as the estimations of the state vector and total disturbance of system (2.1), respectively, and $\hat{{\bf x}}'$ as the redundant estimation. $\sigma\in\mathbb{R}_{\geq 0}$ defines the dead-zone amplitude on the output channel, whose adaptation law is

Note that $\sqrt\sigma$ is always well defined because $\sigma$ is non-negative.

Observer (2.5) is obtained by "dead-zonating" the output errors using a dynamic dead-zone level $\sqrt\sigma$. Around $y-Cz_1 = 0$ and $B^Tz_{i-1}-Cz_i = 0, i = 2, \cdot\cdot\cdot, n$, zero output correction terms provided by the dead zone filter out high frequency noise. However, a fixed dead-zone amplitude will make the tracking and tracked signals never synchronize. $\sigma$ needs to approach 0 fast to ensure convergence to zero. The adaptation law (2.6) weighs two adversarial effects: the first item is to push the dead-zone amplitude $\sigma$ to zero, and the second item is to filter out noise by appropriately increasing $\sigma$ using the output estimation error. Therefore, $\sigma$ converges to 0 fast when $\lambda$ is large. In particular, if there is only the first term, the dead zone function deforms to a linear form in a very short time, and then DZ-CESO deforms to LPESO in ^[18]. On the other hand, setting $w$ large increases the amplitude of the dead zone, thereby improving the ability of noise suppression. Note that the dead-zone amplitude adaptive law (2.6) is different from that in ^[22]. We correct the amplitude using the quadratic sum of the estimation errors of $n$ output channels to have the same threshold. In this way, the estimation error of each second-order observer is considered and the design of observer DZ-CESO is simplified.

Remark 1. The high gain parameter which is defined by $D(l)$, can only grow up to the second order. Thus, the peaking phenomenon and the numerical problems in the implementation which are caused by $l^n$ can be solved. Furthermore, by cutting down the high frequency noise that falls in the dead-zone, the dynamic dead-zone reduces the high sensitivity to measurement noise and improves the noise attenuation. The numerical simulation and frequency domain analysis in Section 4 will show the benefits of the dead-zone nonlinearity by comparing LPESO and DZ-CESO.

3.   Convergence of the DZ-CESO

We study the ISS property of the estimation error for the proposed observer (2.5), and give an upper bound of the estimation error in this section.

Change variables as the following

By the definition of $\mathrm{dz}_{\sqrt\sigma}(\cdot)$, system (2.5) can be transformed as follows

Rescale the variables as

and rewrite the error dynamic system for (2.1) and (2.5) in a compact form:

in which

Define the matrices $G$ and $M$:

where ${\bf 0}$ represents the zero matrix of the corresponding dimension, and

Correspondingly, the adaptation law of $\sigma$ is transformed into

Remark 2. The eigenvalues of $M$ can be arbitrarily assigned by selecting $K_i(i = 1, 2, \cdots, n).$ The constructive procedure was given in the appendix of ^[17]. Based on this algorithm, ^[18] gave a simple selection rule.

Theorem 1. Selecting $(k_{i1}, k_{i2})(i = 1, \cdots, n)$ in system (2.5) makes $M$ defined in (3.3) a Hurwitz matrix. Then there exist $l^* > 1, \lambda > 0, w^* > 0,$ if $l > l^*$ and $0 < w < w^*,$ for any initial conditions ${\bf x}(0)\in \mathbb{R}^n, {\bf z}(0)\in\mathbb{R}^{2n}, \sigma(0)\in\mathbb{R},$ and some positive constants $\mu_i(i = 3, 4, 5, 6)$, the following bounds hold

where

Proof. Using the time-rescaling

on systems (3.2) and (3.5) leads to

Choose $K_i(i = 1, 2, \cdots, n)$ so that $M$ is a Hurwitz matrix. Then solving the Lyapunov equation $PM+M^TP = -I$ yields a positive definite matrix $P\in\mathbb{R}^{2n}$. Define Lyapunov function,

in which $\xi > 0$ is a constant, whose value is determined later. It turns out that

Along the solution of (3.7), take the derivative of $V(\tau, \zeta, \sigma)$ and get that

According to Assumption 1 and Young's inequality, the second term of (3.9) can be enlarged to

For the third term, since $\|D_n^{-1}(l)\|\leq 1$ and $\|\mathrm{sat}_{\sqrt\sigma}(D_n(l)G\zeta)\|\leq \sqrt{n\sigma}$ based on the definition of the norm of the matrix and the vector, it can be written that

Note that

Thus, it is easy to get that

As for the seventh term, it is can be seen that

Now, we calculate the last term, that is

As a result, we have that

In order to make both the first and second expressions of (3.10) negative, let $l\geq l^* > 1,$ and

in which $\rho$ is a positive constant. Then (3.10) can be written as

Let

By using (3.8), (3.12) and (3.13), it leads to that

Since $\tau = lt,$ we have that

By the comparison theorem, it is obtained that

From (3.8) and (3.14), it is concluded that

in which

From (3.1), for $l > 1,$ note that $\frac{1}{l^i}\|\tilde{z}_i\|\leq\|\zeta_i\|\leq\|\tilde{z}_i\|.$ Therefore, we have

Define

Since

combining (3.15)–(3.17), we can obtain the inequalities in (3.6). The proof is complete.

Remark 3. Note that taking $\sigma\equiv 0$ in (2.5), DZ-CESO is reduced to LPESO in ^[18], which indicates that LPESO is a linear form of DZ-CESO. From the proof of Theorem 1, if the matrix $M$ is Hurwitz, the convergence of LPESO can be obtained.

The parameters to be designed for DZ-CESO are $K_i(i = 1, \cdots, n)$ and $w$. To summarize the DZ-CESO design methods discussed in Theorem 1, a parameter tuning procedure is given as follows:

step 1: According to Remark 3, select $K_i$ such that eigenvalues of the matrix $M$ are assigned to the specified positions.

step 2: Based on (3.3) and (3.4), establish matrix $M$ and solve the Lyapunov equation $PM+M^TP = -I$ to obtain the matrix $P$.

step 3: Choose $l^* > 1,$ $\rho > 0$ and $\lambda > 0$.

step 4: Select $\xi$ to satisfy $\xi > \frac{\rho+4n\|P\widehat K\|^2}{ \lambda}.$

step 5: Finally choose $w^* = \frac{1}{8\xi l^{2(n-1)}}$.

4.   Numerical simulations

This section first presents an example to evaluate the effectiveness of the cascade ESO with dead-zone mechanism proposed in Section 2 in terms of total disturbance estimation and noise attenuation. The parameter selection methods of the LESO, LPESO and DZ-CESO are given. Then simulation results of three ESOs are presented to illustrate the advantage of DZ-CESO. At the end of this section, DZ-CESO (4.2) is analyzed in the quasi-frequency domain based on Laplace transform and description function, so as to show its ability of suppressing high-frequency noise more intuitively.

4.1.   Parameter selection of ESOs

The following second-order nonlinear uncertain system in form of (2.1) is considered:

with $d^*(t) = \frac{t}{4\pi}+\sin(4 t+1)$ and $f(x_1(t), x_2(t)) = 5(1-x_1^2(t))x_2(t)-x_1(t)$. The total disturbance is

The control objective is to estimate the total disturbance $d(t, {\bf x})$, and the states $x_1(t), x_2(t)$ despite the measurement noise $v(t)$. We selected ${\bf x}(0) = (0, 0)$ in the simulation. Define the same bounded control action $u(t) = 3\sin(2t)$ for all the tested cases. Measurement noise starts at $t_{s} = 10s$, ends at $t_{e} = 20s$ during the simulation.

Due to total disturbance compensation is the essential purpose of ESO, parameter selection here is based on providing similar reconstruction quality of $d(t, {\bf x})$ at steady state in terms of minimizing integral criterion $\int_{t_0}^T|e_3(t)|\mathrm{d}t$, with $e_3(t)$ being the total disturbance observation error, $t_0 = 25s$ being the integration start time and $T = 30s$ being its finish time.

We implement the proposed DZ-CESO as specified in Section 2, and get that

with the adaption law

According to the parameter tuning procedure given in Section 3, determine the coefficients and parameters to be designed in (4.2) and (4.3). Firstly, the matrix $M$ for (4.2) is

with characteristic polynomial

Place all four of the poles of matrix $M$ at $-1$, and then the coefficients $K_i$ can be set as $k_{11} = 2, k_{12} = 2, k_{21} = 2, k_{22} = 0.5$. Secondly, the matrix $P$ is obtained in the following by solving Lyapunov equation

We obtained $\|P\hat K\|{^2} = 2.7143$. Let $l = 10, \lambda = 10, \rho = 0.01$. According to steps 4 and 5, there is $w = 0.001$. Choose initial conditions as $\hat{x}_1(0) = 0, \eta_1(0) = 5, \hat{x}_2(0) = -5, \eta_2(0) = -5,$ and $\sigma(0) = 5$.

Remark 4. Considering the initial value of $\hat{x}_1(t)$ is generally taken from sensors, so the error $(x_1(0)-\hat{x}_1(0))$ is small. While for the DZ-CESO, there exist other initial errors besides the first term $(x_1(0)-\hat{x}_1(0))$. Therefore, we set the initial value of first state for all ESOs equal to $x_1(0)$ in system (4.1) and keep the other initial states unequal to compare the peaking phenomenon in simulations.

For convenience, we keep the notations concise, and treat the LPESO in ^[18] as case $\mathrm{dz}_{\sqrt{\sigma}}(y(t)-\hat x_1(t)) = y(t)-\hat x_1(t)$, $\mathrm{dz}_{\sqrt{\sigma}}(\eta_1(t)-\hat x_2(t)) = \eta_1(t)-\hat x_2(t)$, and no adaption law (4.3). The coefficients $K_i$ and $l$ are the same as the values in (4.2). The initial state is also placed at $(0, 5, -5, -5).$

Based on (4.1), the LESO can be designed accordingly from ^[13]:

Since the LESO is different from the DZ-CESO and LPESO in structure and number of tuning parameters, we first set $\beta_1 = 3, \; \beta_2 = 3, \; \beta_3 = 1$ to place the poles of the following matrix at $-1$

The initial state is $(z_1(0), z_2(0), z_3(0)) = (0, 5, -5).$ It is found in simulations that gain parameter $l = 10$ provides a similar total disturbance reconstruction quality, as confirmed by Table 1.

4.2.   Performance analysis of ESOs

We perform the following comparison simulations. In the first case, the output $y(t)$ is polluted by "Band-Limited White Noise" with power $1e^{-3}$. Figure 2 shows the comparison of the estimated state and total disturbance of the three observers. As can be seen from Figure 2 that, although the estimations are affected by the measurement noise, the DZ-CESO outperforms the LESO and LPESO in terms of noise attenuation. In particular, for $x_2$ and the total disturbance, estimations of the DZ-CESO are significantly better than the other two methods when high frequency noise is present, despite some lag in tracking speed.

Tables 2–4 show the peakings of estimation errors of $x_1(t), x_2(t)$ and $d(t, {\bf x})$ for three ESOs under noiseless conditions, respectively. It is can be seen that when $l = 10$, there is no significant difference in the error peakings of the three ESOs, although the initial error of the DZ-CESO is larger. In order to characterize the peaking phenomenon, we set $\hat{x}_1(0) = 0.5$ for three ESOs, leaving the other initial values unchanged. Simulations are performed under criteria with similar total disturbance reconstruction qualities, as shown in Table 1. As can be seen from Tables 2–4, with the increase of $l$, the peakings of $e_2(t)$ and $e_3(t)$ provided by the LESO obviously increase, while those provided by LPESO and DZ-CESO barely change. Note that the largest coefficient that needs to be implemented in LPESO and DZ-CESO is $k_{12}l^2 = 1800$, while in the LESO, $l^3 = 27000$. This implies DZ-CESO can solve the peaking phenomenon and the numerical problems in the implementation which are caused by $l^n$.

In order to compare the attenuation effect of the observer on noise with different frequencies, we did a lot of simulations in three different scenarios. All the parameters and initial conditions of ESOs are the same as in Section 4.1. In the scenario (a), the noise is generated by "Band-Limited White Noise" with power $1e^{-3}$. In the scenarios (b) and (c), the measurement noise $v(t)$ is generated by a sinusoidal signal $v(t) = 5\sin(\omega t)$. In the scenario (b), $\omega = 1000$ represents high-frequencies, while in the scenario (c), $\omega = 100$ represents medium frequencies. Tables 5–7 show the effect of the measurement noise on the steady-state behaviour of the three observers, respectively. $\|e_i\|_{\infty}(i = 1, 2, 3)$ represent the maximum estimated errors of states and the total disturbance under measurement noise (from $t = 10s$ to $t = 20s$). We use the error noise ratio (ENR) to measure the extent to which the error is polluted by noise. The ENR is defined as ENR$: = \frac{\|{\bf e}\|_2}{\|{\bf v}\|_2}$. It can be seen from Tables 5–7 that in the scenario (a), $e_2$ and $e_3$ are more seriously polluted by noise than that of $e_1$ for all three ESOs. Compared to LESO and LPESO, the DZ-CESO greatly decreases the error noise ratio of $e_2$ and $e_3$. In the scenario (b), for the observers LPESO and DZ-CESO, the high frequency noise is attenuated on all estimation errors $e_i(t)(i = 1, 2, 3)$. In the scenario (c), the DZ-CESO is superior to LPESO in suppressing medium frequency noise. Through these simulations, the benefits of the dynamic dead-zone mechanism with the low power structure can be recognized.

4.3.   Quasi-frequency domain analysis

The error dynamics system of (4.1) and (4.2) is

where $e_1(t) = \hat x_1(t)-x_1(t), e_2(t) = \eta_1(t)-x_2(t), e_3(t) = \hat x_2(t)-x_2(t), e_4(t) = \eta_2(t)-d(t, {\bf x}).$ Substituting $\dot{d}(t, {\bf x}) = 0$ into (4.5), Laplace transform and description function are used to transform the error system (4.5) into quasi-frequency domain as follows,

in which $s$ is the Laplace variable; $E_1(s), E_2(s), E_3(s)$ and $E_4(s)$ are the outputs of (4.6); $V(s)$ is the measurement noise. All of above are in the frequency domain. $N(E_a)$ and $N(E_b)$ are the describing functions of the dead zone nonlinearity with amplitudes of $E_a(s)$ and $E_b(s)$ as the input, respectively. The describing function of the dead zone nonlinearity in (4.2) is denoted as

The block diagram description of system (4.6) is shown in Figure 3.

Notice that if $\sqrt{\sigma} = 0$ in (4.7), we have $N(E_a) = 1, N(E_b) = 1$ in Figure 3, then the system is reduced to be linear. The transfer functions from $v(t)$ to $e_i(t)(i = 1, 2, 3, 4)$ can be directly derived from Figure 3

The frequency response of the linear system can be easily obtained. If we are mainly concerned with high frequency, only the highest order of numerator and denominator is important. Then it is can be seen from (4.8) that the DZ-CESO in linear form can be approximated as a high order low-pass filter, so it has better noise attenuation ability than LESO. Furthermore, the dead zone nonlinearity on the improvement of noise suppression will be studied in the following.

However, for a nonlinear system, it is not straightforward because the outputs of nonlinear blocks $N(E_a)$ and $N(E_b)$ are related to the amplitudes $E_a$ and $E_b$ of their inputs. Therefore, we use a numerical method which was proposed in ^[24] to calculate the frequency response.

For simplicity of computation, assume that

is known. The following derivation is to obtain the input signal $v(t)$, denoted as $v_0\sin(\omega t+\theta_v)$. When the signal $e_a(t)$ goes through different channels of the block diagram, we can get that

where

in which $|G(s)|$ and $\theta_{G}$ are the magnitude and phase angle of $1/s$, respectively. Denote

where $E_{b}$ and $\theta_{E_b}$ will be determined later. Let the signal $e_b(t)$ go through different channels of the block diagram to obtain that

where

From Figure 3 we can see that

Using the Eqs (4.12) and (4.15), it is easy to get that

Thus, the phase angle and the amplitude of the signal $e_b(t)$ can be obtained after deduction and simplification and are described by

Next, from (4.9) and (4.15), the input signal can be denoted as

Therefore, after deduction and simplification, the phase angle and the amplitude of the signal $v(t)$ are as following

Furthermore, using the aforementioned numerical method and (4.10), (4.13) and (4.15), the phase angles and the amplitudes of outputs of the nonlinear system can be denoted as

At this moment, the magnitude frequency response for the nonlinear system can be described as

which change for various values of the frequency $\omega$ and the dead zone nonlinearity parameter $\sqrt{\sigma}$.

Using the transfer functions for the linear system in (4.8) and the numerical solution for the nonlinear system, the frequency responses of both $|G_{linear}|$ and $|G_{nonlinear}|$ can be achieved. Figure 4 shows the adaptation of the dead zone parameter (left) and the magnitude bode-plots of $|G_{4_{nonlinear}}|$ with different $\sigma$ (right). In this figure, we set $E_{a} = 1$, and other parameters are the same as in Section 4.1. Note that the curve for the the nonlinear system with $\sigma = 0$ is the numerical solution for the linear system. As can be seen from Figure 4 that with an increase in $\sigma$, the magnitude in the frequency response decreases gradually. Thus, increasing $\sigma$ results in the increase of the high frequency noise suppression ability. From this point of view, the DZ-CESO is superior to LPESO in noise suppression ability due to the advantage of the dynamic dead-zone mechanism.

5.   Conclusions

We proposed a cascade dead-zone ESO for $n$th-order nonlinear uncertain systems with measurement noise in this paper. For simplicity, we considered the plant in the phase-variable form. In fact, design method of DZ-CESO can be generalized to address more general forms of observability. Although there is a tradeoff between tracking speed and noise amplification, the low power structure and dynamic dead-zone mechanism improve the estimation effect when there exists high frequency noise. Therefore, a bigger high gain parameter $l$ can be selected to better reject the disturbance. The proposed observer can be used for various settings, such as output regulation, output feedback stabilization and fault detection.

In this paper, an ESO algorithm is designed for continuous compound disturbance and bounded measurement noise. The assumption of bounded derivative of the total disturbance is conservative. In the following work, we will relax this assumption to further improve the DZ-CESO, then design the controller and investigate the stability of the whole closed loop system.

Conflict of interest

The authors have no conflicts of interest.