1.
Introduction
The notion of Lie triple systems was introduced by Lister to obtain all simple Lie triple systems over an algebraically closed field [1]. The cohomology theory of Lie triple systems was investigated by Yamaguti [2]. In 2004, Kubo and Taniguchi gave that Yamaguti cohomology plays a crucial role in the theory of deformations of Lie triple systems [3]. Because of important applications in elementary particle theory and the theory of quantum mechanics, Lie triple systems have been discussed [4,5]. Okubo reformulated the para-statistics as Lie supertriple systems and explained the relationship between Lie supertriple systems and ortho-symplectic supertriple systems [6]. Okubo and Kamiya introduced δ-Jordan Lie supertriple systems in[7]. Some examples and results of Lie supertriple systems were given in [6,8,9]. As a generalization of Lie triple systems and Lie supertriple systems, Cao studied split Lie color triple systems, and obtained the structure of split Lie color triple systems by the techniques of connections of roots in 2019 [10].
The purpose of this paper is to consider the cohomology theory and deformations of Lie color triple systems basing on some work in [2,3,4,11,12,13,14]. The paper is organized as follows. Section 2 is devoted to some basic definitions and the cohomology theory of Lie color triple systems. Section 3 is dedicated to the 1-parameter formal deformation theory of Lie color triple systems. We show that the cohomology group defined in Section 2 is suitable for this 1-parameter formal deformation theory. In Section 4, we study abelian extensions of Lie color triple systems, and get that associated to any abelian extension, there is a representation and a 3-cocycle.
Throughout this paper, we assume that F denotes an arbitrary field.
2.
Preliminaries
Definition 2.1. [15] Let G be an abelian group. A bi-character on G is a map ε:G×G→K∖{0} satisfying
where x,y,z∈G. It is clear that
Definition 2.2. [1] A Lie triple system (T,[⋅,⋅,⋅]) consists of an F-vector space T, a trilinear map [⋅,⋅,⋅]:T×T×T→T, such that for all x,y,z,u,v∈T,
Definition 2.3. [10] A Lie color triple system (T,[⋅,⋅,⋅]) consists of an F-vector space T, a trilinear map [⋅,⋅,⋅]:T×T×T→T, such that for all x,y,z,u,v∈T,
We generalize the notion of the representation of Lie triple systems to Lie color triple systems in the following.
Definition 2.4. Let (T,[⋅,⋅,⋅]) be a Lie color triple system, V an F-vector space and A∈End(V). V is called a (T,[⋅,⋅,⋅])-module with respect to A if there exists a bilinear map θ:T×T→End(V), (a,b)↦θ(a,b) such that for all a,b,c,d∈T,
where D(a,b)=ε(|a|,|b|)θ(b,a)−θ(a,b).
Then θ is called the representation of (T,[⋅,⋅,⋅]) on V with respect to A. In the case θ=0, V is called the trivial (T,[⋅,⋅,⋅])-module with respect to A.
In particular, let V=T, and θ(x,y)(z)=ε(|z|,|x|+|y|)[z,x,y]. Then D(x,y)(z)=[x,y,z] and (2.4), (2.5), (2.6), (2.7) hold. In this case T is showed to be the adjoint (T,[⋅,⋅,⋅])-module and θ is called the adjoint representation of (T,[⋅,⋅,⋅]).
As follows, we give the semidirect product of a Lie color triple system.
Proposition 2.5. Let θ be a representation of a Lie color triple system (T,[⋅,⋅,⋅]) on V with respect to A.Assume the operation [⋅,⋅,⋅]V:(T⊕V)×(T⊕V)×(T⊕V)→T⊕V by
then T⊕V is a Lie color triple system.
Proof. By D(x,y)=ε(|x|,|y|)θ(y,x)−θ(x,y), we get
and
By (2.5), (2.6) and (2.7), it follows that
The calculation above shows that (2.1), (2.2) and (2.3) hold.
Thus, (T⊕V,[⋅,⋅,⋅]V) is a Lie color triple system.
Let θ be a representation of (T,[⋅,⋅,⋅]) on V with respect to A. If an n-linear map f:T×⋯×T⏟ntimes→V satisfies
then f is called an n-cochain on T. Denote by CnA(T,V) the set of all n-cochains, ∀n≥1.
Definition 2.6. For n=1,2,3,4, the coboundary operator dn:CnA(T,V)→Cn+2A(T,V) is defined as follows.
● If f∈C1(T,V), then
● If f∈C2(T,V), then
● If f∈C3(T,V), then
● If f∈C4(T,V), then
Theorem 2.7. The coboundary operator dn defined above satisfies dn+2dn=0, n=1,2.
Proof. From the definition of the coboundary operator, it follows immediately that d3d1=0 implies d4d2=0. Then we only need to prove d3d1=0. In fact, by (2.4)-(2.7), we get
Therefore, the proof is complete.
For n=1,2,3,4, the map f∈CnA(T,V) is called an n-cocycle if dnf=0. We denote by ZnA(T,V) the subspace spanned by n-cocycles and BnA(T,V)=dn−2Cn−2A(T,V).
Since dn+2dn=0, BnA(T,V) is a subspace of ZnA(T,V). Hence we can define a cohomology space HnA(T,V) of (T,[⋅,⋅,⋅]) as the factor space ZnA(T,V)/BnA(T,V).
3.
1-parameter formal deformations of Lie color triple systems
Let (T,[⋅,⋅,⋅]) be a Lie color triple system and F[[t]] be the ring of formal power series over F. Assume that T[[t]] is the set of formal power series over T. We extend an F-trilinear map f:T×T×T→T to be an F[[t]]-trilinear map f:T[[t]]×T[[t]]×T[[t]]→T[[t]] by
Definition 3.1. Let (T,[⋅,⋅,⋅]) be a Lie color triple system over F. A 1-parameter formal deformation of (T,[⋅,⋅,⋅]) is a formal power series mt:T[[t]]×T[[t]]×T[[t]]→T[[t]] of the form
where each mi is an F-trilinear map mi:T×T×T→T (extended to be F[[t]]-trilinear) and m0(x,y,z)=[x,y,z], such that the following equations hold
Conditions (3.1)-(3.3) are called the deformation equations of a Lie color triple system.
Note that T[[t]] is a module over F[[t]] and mt defines the trilinear on T[[t]] such that Tt=(T[[t]],mt) is a Lie color triple system. Now we discuss the deformation equations (3.1)-(3.3).
Conditions (3.1)-(3.2) are equivalent to the following equations
respectively, for i=0,1,2,⋯. The condition (3.3) can be showed as
Then
Using two F-trilinear maps f,g:T×T×T→T (extended to be F[[t]]-trilinear), we assume a map f∘g:T[[t]]×T[[t]]×T[[t]]×T[[t]]×T[[t]]→T[[t]] by
Then the deformation equation (3.3) can be given as
For n=1, m0∘m1+m1∘m0=0.
For n≥2, −(m0∘mn+mn∘αm0)=m1∘mn−1+m2∘mn−2+⋯+mn−1∘αm1.
Section 2 gets that T is the adjoint (T,[⋅,⋅,⋅])-module by setting θ(x,y)(z)=ε(|z|,|x|+|y|)[z,x,y]. In this case, by (3.4)-(3.5), we have mi∈C3(T,T), and mi∘mj∈C5(T,T). In general, if f,g∈C3(T,T), then f∘g∈C5(T,T). Noticing that the definition of coboundary operator dn, we obtain d3mn=m0∘mn+mn∘αm0, for n=0,1,2⋯. Hence the deformation equation (3.3) can be rewritten as
Then m1 is a 3-cocycle and called the infinitesimal of mt.
Definition 3.2. Let (T,[⋅,⋅,⋅]) be a Lie color triple system. Assume that mt(x,y,z)=∑i≥0mi(x,y,z)ti and m′t(x,y,z)=∑i≥0m′i(x,y,z)ti are two 1-parameter formal deformations of (T,[⋅,⋅,⋅]). They are called equivalent, denoted by mt∼m′t, if there is a formal isomorphism of F[[t]]-modules
where each ϕi:T→T is an F-linear map (extended to be F[[t]]-linear) and ϕ0=idT, satisfying
When m1=m2=⋯=0, mt=m0 is said to be the null deformation. A 1-parameter formal deformation mt is called trivial if mt∼m0. A Lie color triple system (T,[⋅,⋅,⋅]) is called analytically rigid, if every 1-parameter formal deformation mt is trivial.
Theorem 3.3. Let mt(x,y,z)=∑i≥0mi(x,y,z)ti and m′t(x,y,z)=∑i≥0m′i(x,y,z)ti be equivalent 1-parameter formal deformations of (T,[⋅,⋅,⋅]). Then m1 and m′1 belong to the same cohomology class in H3(T,T).
Proof. Assume that ϕt(x)=∑i≥0ϕi(x)ti is the formal F[[t]]-module isomorphism and
We get that
In particular,
that is,
Thus m1−m′1=d1ϕ1∈B3(T,T).
Theorem 3.4. Let (T,[⋅,⋅,⋅]) be a Lie color triple system such that H3(T,T)=0. Thus (T,[⋅,⋅,⋅]) is analytically rigid.
Proof. Let mt be a 1-parameter formal deformation of (T,[⋅,⋅,⋅]). Assume that mt=m0+∑i≥nmiti. Then
that is, mn∈Z3(T,T)=B3(T,T). We obtain that there exists fn∈C1(T,T) such that mn=d1fn.
Let ϕt be even, and ϕt=idT−fntn:(T[[t]],mt)⟶(T[[t]],m′t). Note that
Thus ϕt is a linear isomorphism.
Now we consider m′t(x,y,z)=ϕ−1tmt(ϕt(x),ϕt(y),ϕt(z)). It is easy to give that m′t is a 1-parameter formal deformation of (T,[⋅,⋅,⋅]). In fact,
The computations above show that equations (3.1)-(3.3) hold. Using the definition 7, we get mt∼m′t. Assume that m′t=∑i≥0m′iti. Thus
i.e.,
Then we get m′1=⋯=m′n−1=0 and
Hence m′n=mn−d1fn=0 and m′t=m0+∑i≥n+1m′iti. Using induction, this procedure ends with mt∼m0, that is, (T,[⋅,⋅,⋅]) is analytically rigid.
4.
Abelian extensions of Lie color triple systems
In this section, we show that associated to any abelian extension, there is a representation and a 3-cocycle.
An ideal of a Lie color triple system T is a subspace I such that [I,T,T]⊆I. An ideal I of a Lie color triple system is called an abelian ideal if moreover [T,I,I]=0. Notice that [T,I,I]=0 implies that [I,T,I]=0 and [I,I,T]=0.
Definition 4.1. Let (T,[⋅,⋅,⋅]T), (V,[⋅,⋅,⋅]V), and (ˆT,[⋅,⋅,⋅]ˆT) be Lie color triple systems and i:V→ˆT, p:ˆT→T be homomorphisms. The following sequence of Lie color triple systems is a short exact sequence if Im(i)=Ker(p), Ker(i)=0 and Im(p)=T,
In this case, we show ˆT an extension of T by V, and denote it by EˆT. It is called an abelian extension if V is an abelian ideal of ˆT, i.e., [u,v,⋅]ˆT=[u,⋅,v]ˆT=[⋅,u,v]ˆT=0, for all u,v∈V.
A section σ:T→ˆT of p:ˆT→T consists of the linear map σ:T→ˆT such that p∘σ=idT.
Definition 4.2. Two extensions of Lie color triple systems EˆT:0⟶Vi⟶ˆTp⟶T⟶0 and E˜T:0⟶Vj⟶˜Tq⟶T⟶0 are equivalent. If there exists a Lie color triple system homomorphism F:ˆT→˜T such that the following diagram commutes
Let ˆT be an abelian extension of T by V, and a linear mapping σ:T→ˆT be a section. Define maps T⊗T→End(V) by
Clearly, the following fact holds, i.e.,
for all (x1,x2)∈T⊗T,u∈V.
Theorem 4.3. Using the above notations, (V,θ) is a representation of Tand does not depend on the choice of the section σ. Moreover, equivalent abelian extensions give the same representation.
Proof. First, if we choose another section σ′:T→ˆT, then
for some ui∈V.
Note that [u,v,⋅]ˆT=0=[u,⋅,v]ˆT for all u,v∈V, this yields that
This shows that θ is independent on the choice of σ.
Second, we get that (V,θ) is a representation of T.
By the equality
it follows that
Thus, we obtain (2.5) holds.
Similarly, by the equality
we have
by the equality
we get
Thus, we know that (2.6) and (2.7) hold. Therefore, it is proved that (V,θ) is a representation of T.
Third, we will show equivalent abelian extensions give the same θ.
Assume that EˆT and E˜T are equivalent abelian extensions, and F:ˆT→˜T is the Lie color triple system homomorphism satisfying F∘i=j, q∘F=p. Choosing linear sections σ and σ′ of p and q, we have qFσ(xi)=pσ(xi)=xi=qσ′(xi), then Fσ(xi)−σ′(xi)∈Ker(q)≅V. Moreover,
The proof is complete.
Let σ:T→ˆT be a section of the abelian extension. Assume the following map:
for all x1,x2,x3∈T.
Theorem 4.4. Let 0⟶V⟶ˆT⟶T⟶0 be an abelian extension of T by V. Then ω defined by (4.4) is a 3-cocycle of T with coefficients in V, where the representation θ is given by (4.3).
Proof. By the equality
The left hand side shows that
Similarly, the right side is equal to
Thus, it follows that
Therefore, ω is a 3-cocycle.
Acknowledgments
Supported by NNSF of China (No.11801211), Science Foundation of Heilongjiang Province(No.QC2016008), the Fundamental Research Funds in Heilongjiang Provincial Universities (No.145109128).
Conflict of interest
The authors declare there is no conflicts of interest.









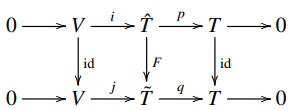



 DownLoad:
DownLoad: