Complicate dynamics of a discrete predator-prey model with double Allee effect

1.   Introduction

The dynamical analysis of complex ecosystem, such as food chain, is based on the interaction among species or between two species, especially the dynamical relationship between predator and prey ^[1,2,3,4]. The current theory of predator-prey dynamics must depend on the study of nonlinear mathematical model ^[5]. With the continuous improvement of ecological knowledge like theoretical research, empirical research and observational research, etc., there are more and more basic elements of predation to be considered. Therefore, modelers add some complexities to their abstraction in order to obtain authenticity from the emergence of the far-reaching Lotka-Volterra model^[6] and the modifications introduced by Volterra^[5], taking into account the self-interference of prey populations.

Allee effect, which affects the number of prey, is one of these factors. It changes the qualitative stability and quantitative aspects of predator-prey model dynamics. Because the interaction between predator and prey is naturally prone to vibration, it is obvious to study this phenomenon as a potential mechanism for the generation of population cycles. Lots of researches about predator-prey models are done with the Allee effect^[7,8,9].

The most popular framework for modeling expert predator-prey interaction has the following structure:

where $x(t)$ and $y(t)$ are the prey and predator population sizes in the time $t$, respectively, $p, c > 0$ indicate the birth rate and background mortality rate, respectively, $g(x, k)$ describes the specific growth rate of the prey in the absence of predator, and $h(x)$ describes the predator functional response.

Any mechanism leading to a positive correlation between the components of individual fitness and the number or density of similar individuals can be regarded as Allee effect; it describes a scenario in which low population size is affected by the positive correlation between population growth rate and density, increasing the possibility of their extinction.

Recent ecological studies have shown that two or more Allee effects can lead to mechanisms acting on a population at the same time. The combined effects of some of these phenomena are called multiple (double) Allee effects. The author's analysis in^[10] showed that the results of strong and weak Allee effects on the dynamics of Volterra predator-prey model are similar, which originate from the limit cycle of the model.

In this paper, we continue to consider the following predator-prey model with double Allee effect functional response raised by^[10].

where $r$ scales the prey growth rate, $K$ is the intrinsic carrying capacity for the environment to the prey in the absence of predator, $M$ is the Allee threshold, and the auxiliary parameter $N$ satisfies $N > 0$, $q$ is the prey captured rate by the predator, $p, C > 0$ indicate the birth rate and background mortality rate, respectively.

One can see that the first equation in the model (1.2) includes double Allee effects, expressed by the first factor $m(X) = X-M$, and a second term $r(X) = \frac{rX}{X+N}$, This can be interpreted as an approximation of population dynamics, in which the difference between fertile and non-fertile are not clearly modeled.

In order to simplify the analysis of system (1.2), we make a topologically equivalent change of variables and time rescaling as in^{[11,12,13,14]}, defining the function $\phi$, such that $\phi(x, y) = ({K}{x}, \frac{r}{q}y) = (X, Y)$, $\frac{r}{x+n}dT = dt$. Then, system (1.2) is transformed into

where $b = \frac{pK}{r}$, $\frac{C}{pK}$, $m = \frac{M}{K}$, $n = \frac{N}{K}$, and $K > X > M$ is obtained from equation (1.2), so $1 > m > 0$.

We now use the semidiscretization method, which has been applied in many studies^{[15,16,17,18]}, to study the discrete model of system (1.3). For this, suppose that $[t]$ denotes the greatest integer not exceeding $t$. Consider the following semidiscretization version of (1.3).

It is easy to see that the system (1.4) has piecewise constant arguments, and that a solution $(x(t), y(t))$ of the system (1.4) for $t \in [0, +\infty)$ possesses the following natures:

1. on the interval $[0, +\infty)$, ${ x(t)}$ and ${ y(t)}$ are continuous;

2. when $t\in[0, +\infty)$ except for the points $t\in\{0, 1, 2, 3, \cdots\}$, $\frac{d x(t)}{dt}$ and $\frac{d y(t)}{dt}$ exist everywhere.

The following system can be obtained by integrating (1.4) over the interval $[n, t]$ for any $t\in[n, n+1)$ and $n = 0, 1, 2, \cdots$

where $x_n = x(n)$ and $y_n = y(n)$. Letting $t\to (n+1)^-$ in (1.5) produces

where $b, c, n > 0$, $1 > m > 0$ are the same as in (1.3). We mainly study the properties of system (1.6) in the sequel.

The rest of the paper is organized as follows: In Section 2, we investigate the existence and stability of fixed points of the system (1.6). In Section 3, we derive the sufficient conditions for the transcritical bifurcation and the Neimark-Sacker bifurcation of the system (1.6) to occur. In Section 4, numerical simulations are performed to verify the above obtained theoretical results and reveal some new dynamical properties.

Before we analyze the fixed points of the system (1.6), we recall the following lemma see ^[16,19].

Lemma 1.1. Let $F(\lambda) = \lambda^2+P\lambda+Q$, where $P$ and $Q$ are two real constants. Suppose $\lambda_1$ and $\lambda_2$ are two roots of $F(\lambda) = 0$. Then the following statements hold.

(ⅰ) If $F(1) > 0,$ then

(ⅰ.1) $|\lambda_1| < 1$ and $|\lambda_2| < 1$ if and only if $F(-1) > 0$ and $Q < 1$;

(ⅰ.2) $\lambda_1 = -1$ and $\lambda_2\ne-1$ if and only if $F(-1) = 0$ and $P\ne2$;

(ⅰ.3) $|\lambda_1| < 1$ and $|\lambda_2| > 1$ if and only if $F(-1) < 0$;

(ⅰ.4) $|\lambda_1| > 1$ and $|\lambda_2| > 1$ if and only if $F(-1) > 0$ and $Q > 1$;

(ⅰ.5) $\lambda_1$ and $\lambda_2$ are a pair of conjugate complex roots with $|\lambda_1| = |\lambda_2| = 1$ if and only if $-2 < P < 2$ and $Q = 1$;

(ⅰ.6) $\lambda_1 = \lambda_2 = -1$ if and only if $F(-1) = 0$ and $P = 2$.

(ii) If $F(1) = 0,$ namely, $1$ is one root of $F(\lambda) = 0$, then the another root $\lambda$ satisfies $|\lambda| = (<, > )1$ if and only if $|Q| = (<, > )1.$

(iii) If $F(1) < 0,$ then $F(\lambda) = 0$ has one root lying in $(1, \infty)$. Moreover,

(iii.1) the other root $\lambda$ satisfies $\lambda < ( = )-1$ if and only if $F(-1) < ( = )0$;

(iii.2) the other root $-1 < \lambda < 1$ if and only if $F(-1) > 0$.

2.   Existence and stability of fixed points

In this section, we first consider the existence of fixed points and then analyze the local stability of each fixed point.

The fixed points of the system (1.6) satisfy

Considering the biological meanings of the system (1.6), one only takes into account nonnegative fixed points. Thereout, one finds that the system (1.6) has and only has four nonnegative fixed points $E_{0} = (0, 0)$, $E_{1} = (1, 0)$, $E_{2} = (m, 0)$ and $E_{3} = (x_{0}, y_{0})$ for $m < c < 1$, where

The Jacobian matrix of the system (1.6) at any fixed point $E(x, y)$ takes the following form

where $A = e^{(1-x)(x-m)-(x+n)y}$.

The characteristic polynomial of Jacobian matrix $J(E)$ reads

where

$p = Tr(J(E)) = [1+x(-2x-y+m+1)]e^{A}+e^{b(x-c)(x+n)},$ $q = Det(J(E)) = [1+x(-2x-y+m+1)][bx(x+n)(2x+n-c)]e^{A+b(x-c)(x+n)}.$

For the stability of fixed points $E_0$, $E_1$, $E_2$ and $E_3$, we can easily get the following Theorems 2.1-2.4 respectively.

Theorem 2.1. The fixed point $E_0 = (0, 0)$ of the system (1.6) is a sink.

Proof. The Jacobian matrix $J({E_0})$ of the system (1.6) at the fixed point $E_0 = (0, 0)$ is given by

Obviously, $|\lambda_1| = e^{-m} < 1$ and $|\lambda_2| = e^{-bcn} < 1$, so $E_0 = (0, 0)$ is a sink.

Theorem 2.2. The following statements about the fixed point $E_1 = (1, 0)$ of the system (1.6) are true.

1. If $c < 1$, then $E_1$ is a saddle.

2. If $c = 1$, then $E_1$ is non-hyperbolic.

3. If $c > 1$, then $E_1$ is a stable node.

Proof. The Jacobian matrix of the system (1.6) at $E_1 = (1, 0)$ is

Obviously, $\lambda_1 = m$ and $\lambda_2 = e^{b(1-c)(1+n)}$.

Note $|\lambda_1| < 1$ is always true. If $c < 1$, then $|\lambda_2| > 1$, so $E_1$ is a saddle; if $c = 1$, then $|\lambda_2| = 1$, therefore $E_1$ is non-hyperbolic; if $c > 1$, implying $|\lambda_2| < 1$, then $E_1$ is a stable node, namely, a sink. The proof is complete.

Theorem 2.3. The following statements about the fixed point $E_2 = (m, 0)$ of the system (1.6) are true.

1. If $c < m$, then $E_2$ is a source.

2. If $c = m$, then $E_2$ is non-hyperbolic.

3. If $c > m$, then $E_2$ is a saddle.

Proof. The Jacobian matrix of the system (1.6) at $E_2 = (m, 0)$ is

Obviously, $\lambda_1 = -m^{2}+m+1$ and $\lambda_2 = e^{b(m-c)(m+n)}$.

Note $0 < m < 1$, so $|\lambda_1| > 1$ is always true. If $c < m$, then $|\lambda_2| > 1$, so $E_2$ is a source; if $c = m$, then $|\lambda_2| = 1$, therefore $E_2$ is non-hyperbolic; if $c > m$, implying $|\lambda_2| < 1$, then $E_2$ is a saddle. The proof is finished.

Theorem 2.4. When $(1-c)(c-m) > 0$, namely, $0 < m < c < 1$, the fixed point $E_3 = (c, \frac{(1-c)(c-m)}{c+n})$ is a positive fixed point of the system (1.6). Let $b_{0} = \frac{c^{2}+2cn-mn-m-n}{(c+n)^{2}(1-c)(c-m)}$. Then the following statements are true about the positive fixed point $E_3$.

Ⅰ. If $m < \frac{c^2+2cn-n}{n+1}$, then,

1. for $0 < b < b_{0}$, $E_3$ is a stable node;

2. for $b = b_{0}$, $E_3$ is non-hyperbolic;

3. for $b > b_{0}$, $E_3$ is an unstable node.

Ⅱ. If $m\ge\frac{c^2+2cn-n}{n+1}$, then, $E_3$ is an unstable node.

Proof. The Jacobian matrix of the system (1.6) at $E_3$ can be simplified as follows

The characteristic polynomial of Jacobian matrix $J({E_3})$ reads as

where

$p = Tr(J({E_3})) = 2-b_{0}c(1-c)(c-m)(c+n),$

$q = Det(J({E_3})) = 1+(b-b_{0})c(1-c)(c-m)(c+n).$ By calculating we get

$F(1) = bc(1-c)(c-m)(c+n) > 0,$

and

Ⅰ. If $m < \frac{c^2+2cn-n}{n+1}$, then $b_0 > 0$. So, when $0 < b < b_{0}$, $q < 1$. By Lemma 1.1 $(i.1)$, $|\lambda_1| < 1$ and $|\lambda_2| < 1$, therefore $E_3$ is a stable node, i.e., a sink. When $b = b_{0}$, $q = 1$, $-2 < p < 2$. By Lemma 1.1 $(i.5)$, Eq. (2.1) has a pair of conjugate complex roots $\lambda_1$ and $\lambda_2$ with $|\lambda_1| = |\lambda_2| = 1$, implying $E_3$ is non-hyperbolic. When $b > b_{0} <$, $q > 1$. Lemma 1.1 $(i.4)$ tells us that $|\lambda_1| > 1$ and $|\lambda_2| > 1$, so $E_3$ is an unstable node, i.e., a source.

Ⅱ. If $m\ge\frac{c^2+2cn-n}{n+1}$, then $b_0\le0$. So, $b > 0\ge b_0$. Hence $q > 1$. Lemma 1.1 $(i.4)$ reads that $E_3$ is an unstable node. The proof is complete.

3.   Bifurcation analysis

In this section, we are in a position to use the Center Manifold Theorem and bifurcation theorem to analyze the local bifurcation problems of the fixed points $E_1$, $E_2$ and $E_3$. For related work, refer to^{[20,21,22,23,24,25]}.

3.1.   For fixed point $E_1=(1, 0)$

Theorem 2.2 shows that a bifurcation of $E_{1}$ may occur in the space of parameters $(b, c, m, n) \in S_{E_{+}} = \{(b, c, m, n) \in R^4_{+}| b > 0, c > 0, 1 > m > 0, n > 0 \}$.

Theorem 3.1. Set the parameters $(b, c, m, n) \in S_{E_{+}} = \{(b, c, m, n) \in R^4_{+}| b > 0, c > 0, 1 > m > 0, n > 0 \}$. Let $c_0 = 1$, then the system (1.6) undergoes a transcritical bifurcation at $E_1$ when the parameter $c$ varies in a small neighborhood of $c_0$.

Proof. In order to show the detailed process, we proceed according to the following steps.

The first step. Let $u_n = x_n-1, v_n = y_n-0$, which transforms the fixed point $E_1 = (1, 0)$ to the origin $O(0, 0)$, and the system (1.6) to

The second step. Giving a small perturbation $c^*$ of the parameter $c$, i.e., $c^* = c-c_0$, with $0 < | c^* |\ll 1$, the system (3.1) is perturbed into

Letting $c_{n+1}^* = c_n^* = c^*,$ the system (3.2) can be written as

The third step. Taylor expanding of the system (3.3) at $(u_n, v_n, c_n^*) = (0, 0, 0)$ takes the form

where $\rho_1 = \sqrt {u_n^2+v_n^2+(c_n^*)^2},$

Let

$\quad i.e., J(E_{1}) = \begin{pmatrix} m & -(n+1) & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}.$ Then, we derive the three eigenvalues of $J(E_{1})$ to be

and the corresponding eigenvectors

The fourth step. Let $T = \begin{pmatrix} \xi_1 & \xi_2 & \xi_3\\[5pt] \eta_{1} & \eta_{2} & \eta_{3}\\[5pt] \varphi_{1} & \varphi_{2} & \varphi_{3} \end{pmatrix},$ namely,

Taking the following transformation

the system (3.4) is changed into the following form

where $\rho_2 = \sqrt{X_{n}^{2}+Y_{n}^{2}+\delta_n^{2}}$,

The fifth step. Suppose on the center manifold

where $\rho_3 = \sqrt {Y_n^2+\delta_n^2}$, then, according to

and $X_{n+1} = h(Y_{n+1}, \delta_{n+1}),$ we obtain the center manifold equation to satisfy the following relation

$mh(Y_n, \delta_n)+F(h(Y_n, \delta_n), Y_{n}, \delta_n)\\[5pt] = h_{20}{(Y_{n}+G(h(Y_n, \delta_n), Y_{n}, \delta_n))}^{2}\\[5pt]+h_{11}{(Y_{n}+G(h(Y_n, \delta_n), Y_{n}, \delta_n))}\delta_n +h_{02}\delta_n^2+o(\rho_3^2).$

Comparing the corresponding coefficients of terms with the same orders in the above center manifold equation, we get

$h_{20} = \frac{(m-2)(1+n)^{2}-(1+n)(2+n)(m-1)-b(1+n)^{3}}{1-m},$

$h_{11} = \frac{b(1+n)^{2}}{1-m}, h_{02} = 0.$

So, the system (3.5) restricted to the center manifold takes as

$Y_{n+1} = f(Y_n, \delta_n): = Y_{n}+G(h(Y_n, \delta_n), Y_{n}, \delta_n)+ o(\rho_3^2)\\ = Y_n+b(1+n)^{2}Y_{n}^2-b(1+n){Y_{n}} \delta_{n}\\+\frac{b(1+n)^{2}}{1-m}\Big(1-2m-n-\frac{1}{2}b(1+n)^{2}(1+m)\Big)Y_{n}^3\\+\big(\frac{mb^{2}(1+n)^{3}}{1-m}-b(1+n)\big){Y_{n}}^{2}\delta_{n}+\frac{1}{2}b^{2}(1+n)^{2}Y_n\delta_{n}^{2}\\+o(\rho_3^3).$

Therefore one has

According to (21.1.42)-(21.1.46) in the literature (^[26], pp. 507), all the conditions for the occurrence of the transcritical bifurcation are established, hence, it is valid for the {occurrence} of transcritical bifurcation in the fixed point $E_{1}$. The proof is over.

3.2.   For fixed point $E_2=(m, 0)$

According to Theorem 2.3, the fixed point $E_2(m, 0)$ is non-hyperbolic, the system (1.6) may undergo a bifurcation (the correspond eigenvalue are $\lambda_1 = -m^{2}+m+1$, $\lambda_2 = 1$). By using the same method as that in Section 3.2, we get the following result.

Theorem 3.2. Set the parameters $(b, c, m, n) \in S_{E_{+}} = \{(b, c, m, n) \in R^4_{+}| b > 0, c > 0, 1 > m > 0, n > 0 \}$. Let $c_1 = m$, then the system (1.6) undergoes a transcritical bifurcation at $E_2$ when the parameter $c$ varies in a small neighborhood of $c_1$.

3.3.   For fixed point $E_3=(c, \frac{(1-c)(c-m)}{c+n})$

When $m < \frac{c^2+2cn-n}{n+1}$, $b = b_{0} = \frac{c^{2}+2cn-mn-n-m}{(c+n)^{2}(1-c)(c-m)}$, Theorem 2.4 with Lemma 1.2 $(i.5)$ shows that $F(1) > 0$, $F(-1) > 0$, $-2 < p < 2$ and $q = 1$, so $\lambda_1$ and $\lambda_2$ are a pair of conjugate complex roots with $|\lambda_1| = |\lambda_2| = 1$. At this time we derive that the system (1.6) at the fixed point $E_{3}$ can undergo a Neimark-Sacker bifurcation in the space of parameters $(b, c, m, n) \in S_{E_{+}} = \{(b, c, m, n) \in R^4_{+}|b > 0, 1 > c > m, 0 < m < \frac{c^2+2cn-n}{n+1} \}.$

In order to show the process clearly, we carry out the following steps.

The first step. Take the changes of variables $u_n = x_n-x_{0}, v_n = y_n-y_{0}$, which transform fixed point $E_3 = (x_{0}, y_{0})$ to the origin $O(0, 0)$, and the system (1.6) into

The second step. Give a small perturbation $b^*$ of the parameter $b$, i.e., $b^* = b-b_0$, then the perturbation of the system (3.6) can be regarded as follows

The corresponding characteristic equation of the linearized equation of the system (3.7) at the equilibrium point (0, 0) can be expressed as

where

and

$q(b^*) = \frac{c[(c^2+2cn-mn-m-n)-(b^*+b_0)(c+n)^2(1-c)(c-m)]}{-(c+n)}+1.$

It is easy to derive $p^2(b^*)-4q(b^*) < 0$ when $b^* = 0$, and $0 < p(b^*) < 2$, then the two roots of $F(\lambda) = 0$ are

which implies

and

The occurrence of Neimark-Sacker bifurcation requires the following conditions to be satisfied

Since ${p(b^*)}\big|_{b^* = 0} = 2+\frac{c(-c^2-2cn+mn+m+n)}{c+n}$ and ${q(b^*)}\big|_{b^* = 0} = 1$, we have $\lambda_{1, 2}(0) = \frac{2(c+n)+c(-c^2-2cn+mn+m+n)\pm i\sqrt{4(c+n)^2-[2(c+n)+c(-c^2-2cn+mn+m+n)]^2}}{2(c+n)}$, then it is easy to derive $\lambda_{1, 2}^i(0)\ne1$ for all $i = 1, 2, 3, 4$. According to (^[2], pp517-522), they satisfy all of the conditions for Neimark-Sacker bifurcation to occur.

The third step. In order to derive the normal form of the system (3.7), we expand the system (3.7) into power series up to the following third-order form around the origin

where $\rho_4 = \sqrt {u_n^2+v_n^2},$

Let

It is easy to derive the two eigenvalues of the matrix $J(E_{3})$ are

where $K = \frac{c(-c^2-2cn+mn+m+n)}{c+n}$,

$\beta = \frac{\sqrt{-c(-c^2-2cn+mn+m+n)[4(c+n)+c(-c^2-2cn+mn+m+n)]}}{2(c+n)},$

with the corresponding eigenvectors

$v_{1, 2} = \begin{pmatrix} -c(c+n) \\ -\frac{1}{2}K \end{pmatrix} \pm i \begin{pmatrix} 0 \\ \beta \end{pmatrix}$.

Let

Make a change of variables

then, the system (3.8) is transformed into the following form

where $\rho_5 = \sqrt {X^2+Y^2},$

Furthermore,

The {fourth} step. In order to ensure that the system (3.9) has a Neimark-Sacker bifurcation occurring, we need to calculate the discriminating quantity

and $L$ is required not to be zero, where

By calculation we get

Theorem 3.3. Assume the parameters $b$, $c$, $m$, $n$ in the space $S_{E_{+}} = \{(b, c, m, n) \in R^4_{+}|b > 0, 1 > c > m, 0 < m < \frac{c^2+2cn-n}{n+1}\}.$ Let $b_{0} = \frac{c^2+2cn-mn-m-n}{(c+n)^2(1-c)(c-m)}$ and $L$ be defined as above $(3.10)$. If $L\ne0$ holds and the parameter $a$ varies in the small neighborhood of $b_0$, then the system (1.6) at the fixed point $E_3$ undergoes a Neimark-Sacker bifurcation. In addition, if $L < (or > )0$, then an attracting (or repelling) invariant closed curve bifurcates from the fixed point $E_3$ for $b < (or > ) b_{0}$.

4.   Numerical simulation

In this section, we use the bifurcation diagrams, phase portraits and Lyapunov exponents of the system (1.6) to verify our theoretical results and further reveal some new dynamical behaviors to occur as the parameters vary by Matlab software.

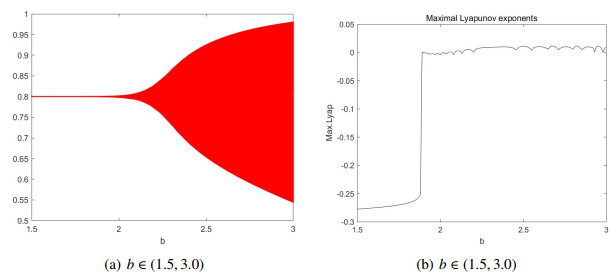
Fix the parameter values $c = 0.8, m = 0.3, n = 0.8$, let $b \in (1.5, 3.0)$ and take the initial values $(x_{0}, y_{0}) = (0.55, 0.25), (0.80, 0.05)$ in Fig. 2 and Fig. 3 respectively. Figure 1(a) shows the {bifurcation} diagram of $(b, x)$-plane, from which the fixed point $E_{3}$ is stable when $b < b_{0} = 2.266$. Moreover, the fixed point $E_{3}$ is unstable when $b > b_{0}$. Hence, the Neimark-Sacker bifurcation occurs at the fixed point $E_{3} = (0.800, 0.625)$ when $b = b_{0}$, whose multipliers are $\lambda_{1, 2} = 0.855\pm 0.519 i$ with $|\lambda_{1, 2}| = 1$.

The corresponding maximum Lyapunov exponent diagram of the system (1.6) is plotted in Figure 1(b). Figures 2(a)-2(f) and Figures 3(a)-3(d) show that the dynamical properties of the fixed point $E_3$ change from stable to unstable as the value of the parameter $b$ decreases and there is an occurrence of invariant closed curve around $E_3$ when $b = b_{0}$, which agrees to the result of Theorem 3.3.

From the phase portraits in Figs 2 and 3, we infer the stability of $E_{3}$. Figures 2(d)-2(f) show that the closed curve is stable outside, while Figures 3(a)-3(d) indicate that the closed curve is stable inside for the fixed point $E_{3}$ as long as the assumptions of Theorem 3.2 hold.

5.   Discussion and conclusion

In this paper, we discuss the dynamical behaviors of a predator-prey model (1.6) of Gause-type with double Allee effect affecting the prey population. Under the given parametric conditions, we completely show the existence and stability of four nonnegative equilibria $E_{0} = (0, 0)$, $E_{1} = (1, 0)$, $E_{2} = (m, 0)$ and $E_{3} = (c, \frac{(1-c)(c-m)}{c+n})$. Then we derive the sufficient conditions for its transcritical bifurcation and Neimark-Sacker bifurcation to occur. Meanwhile, it is clear that the positive equilibrium $E_{3} = (x_{0}, y_{0})$ is asymptotically stable when $b < b_{0} = \frac{c^2+2cn-mn-m-n}{(c+n)^2(1-c)(c-m)}$ and unstable when $b > b_0$ under the condition $m < \frac{c^2+2cn-n}{n+1}$. Hence, the system (1.6) undergoes a bifurcation which has been shown to be a Neimark-Sacker bifurcation when the parameter $b$ goes through the critical value $b_{0}$. Finally, numerical simulations illustrate the theoretical analysis results of the system (1.6).

The perturbations of different parameters in this system may lead to different bifurcations. This demonstrates that this system is sensitive to its parameters. Especially, the occurrence of Neimark-Sacker bifurcation implies that the predator and the prey can coexist under such parametric conditions.

Authors' contributions

All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.

Acknowledgment

This work is partly supported by the National Natural Science Foundation of China (61473340), the Distinguished Professor Foundation of Qianjiang Scholar in Zhejiang Province, and the National Natural Science Foundation of Zhejiang University of Science and Technology (F701108G14).

Conflict of interest

The authors declare that they have no competing interests.