Exponential stability of time-delay systems with highly nonlinear impulses involving delays

1.   Introduction

Impulsive systems represent a special type of dynamical system whose evolution is influenced not only by continuous-time dynamics but also by instantaneous abrupt changes occurring at certain specific moments. Such systems are widely used in mathematical modeling to describe real-world phenomena with sudden transitions, such as the transmission of information ^[1,2], genetic regulation ^[3], communication networks ^[4,5], and so on. The study of impulsive systems can be divided into two main aspects: impulsive control problems and impulsive disturbance problems. These two aspects examine the positive regulatory effects of impulses on systems and their potential disruptive impacts, thereby revealing the complex dynamical characteristics of impulsive systems.

Impulsive control problems focus on the intentional design of impulsive inputs to actively intervene in systems, improving their dynamic performance or achieving stabilization goals. This control approach is particularly useful for systems whose continuous dynamics are inherently unstable or difficult to stabilize using conventional methods. On the other hand, impulsive disturbance problems investigate the effects of abrupt external events on systems, focusing on the potential destabilization they may cause. This aspect often involves robustness analysis, assessing a system's ability to maintain stability under uncontrollable impulsive influences, or exploring ways to minimize the risk of instability. Due to the dual effects of impulses, the stability analysis on impulsive systems becomes more complicated. Recently, numerous significant studies on the stability issues of impulsive systems have been reported in ^[6,7,8,9].

Time delays arise frequently in many science and engineering systems, including temperature control ^[10], neural networks ^[11], biology ^[12], and the milling process ^[13], which occur not only in continuous dynamics, but also in the process of sampling and transmitting impulsive information across various real-world cases, see ^[14,15,16]. It is well known that in many practical applications, the presence of delays may disrupt the timely response of a system to its states, significantly deteriorating the stability of systems and leading to undesired performance such as oscillation and chaos (see ^[17,18,19]). However, it is more noteworthy that the presence of delays may also have positive effects on the behavior of the systems, i.e., they may contribute to the stability of systems and achieve better performance (see the references ^[20,21]). Similarly, the delays in impulses can also have dual (positive and negative) effects. For example, in the impulsive braking system of a train, due to delays in sensor and signal processing, the actual deceleration after each braking impulse is smaller than it would be without the delays. This demonstrates that delays in impulses have a stabilizing effect, contributing to the train's deceleration process.

These days, there is a growing interest in the study of systems with impulses involving dual effects of delays (see the works ^{[22,23,24,25,26]}). Among them, the works ^[22,23,24] only considered the stabilizing effects of delays in impulses on the stability of systems. The authors in ^[25] presented sufficient conditions on the basis of Lyapunov methods for exponential stability of nonlinear systems, which has given a way to demonstrate the dual effects of delays in impulses. Unfortunately, the delays in continuous dynamics were not considered. Although authors in ^[26] considered delays in continuous dynamics and utilized the average time delay method to show the dual effects of delays in impulses, it imposed the condition that delays in continuous dynamics must exceed those in impulses, which introduces certain constraints. So it is evident that the delays in continuous dynamics are often restricted when investigating the dual effects of delays in impulses. How to remove those unnecessary restrictions on delays in continuous dynamics is a challenging topic.

In recent years, the research of impulsive systems has been widely developed. For example, the authors in ^[9] studied the locally exponential stabilization of nonlinear systems, where the design of hybrid control fully considered the limitation of saturation and the correction effects of impulses. The stability problem of impulsive delayed systems was investigated based on Razumikhin method and inequality method respectively in ^[16,29]. The authors in ^[15] considered nonlinear differential systems with impulses involving state-dependent delay, and established several stability criteria. With the development of impulsive control theory, the related research has been extended to stochastic systems ^[3], switched systems ^[14], fuzzy systems ^[28], and so on. Moreover, in addition to the traditional Lyapunov stability, some results on finite-time stability and input-to-state stability of impulsive systems have also been reported, see ^[8,27]. However, note that the existing stability results for nonlinear systems with impulses ^{[3,8,9,14,15,16,27,28,29]} share a common conservative requirement that the increase or decay of the energy function at impulsive instants is restricted by a linear form. This constraint restricts the applicability of the classical results only to systems with linear or nonlinear impulses whose Euclidean norm is constrained by a linear constant (i.e., meet the linear conditions). However, in reality, impulses without the linear conditions, referred to as highly nonlinear impulses, are often encountered. For instance, in a system of financial markets, the change of a policy announcement (such as interest rate adjustments or sudden regulatory actions) can cause abrupt sell-offs or buying surges, creating volatile and unpredictable fluctuations that produce nonlinear impacts on the market, which can be seen as classic examples of highly nonlinear impulsive disturbances. In real-world applications, highly nonlinear impulses may be the source of the degradation of performance and bring a greater challenge to the study of the systems' behavior. Therefore, how to relax the linear restriction in discrete dynamics so that they can be used to solve more complicated situations, such as the stability of systems with highly nonlinear impulses, is an important and unsolved issue.

Inspired by the aforementioned analysis, this article aims to propose an improved Razumikhin approach studying the LES property of time-delay systems with delayed impulses. A new Razumikhin-type theorem is proposed to remove those restrictions on delays in continuous dynamics, where the dual effects of delays in impulses are comprehensively fetched and incorporated into the dynamic analysis of the systems. On the other hand, the nonlinear rate in discrete dynamics is fully taken into consideration, in which a relationship between impulses, continuous dynamics, and the initial region is revealed. As an application, the stability of certain time-delay systems with highly nonlinear delayed impulses is studied. Some conditions in the form of LMIs are established to achieve the LES of the concerned systems. The results show that at the same impulsive frequency, the impulsive effects no longer depend only on the impulsive strength parameters, but also depend on the high nonlinearity of the impulses, which is a distinct feature compared to the existing stability results of impulsive systems.

This article is organized as follows. Section 2 outlines the nonlinear delayed system and introduces the relevant notation. Some Razumikhin theorems are proposed in Section 3. Section 4 explores applications. Section 5 includes examples to showcase the practical applicability of the results. Eventually, the conclusion is stated in Section 6.

2.   Preliminaries

Notations. Let $\mathbb{R}$, $\mathbb{R}_{+}$, and $\mathbb{Z}_{+}$ denote the set of real numbers, nonnegative real numbers, and positive integers, respectively. $\mathbb{R}^{n}$ is the $n-$dimensional real space equipped with the Euclidean norm $|\cdot|$. For some real symmetric matrices $G$ and $H$, $G\leq H$ (respectively, $G < H$) indicates that $G-H$ is negative semidefinite (respectively, negative definite). $I_{j}$ denotes the identity matrix of $j$ dimensions and $\star$ denotes the symmetric block in the matrix. Set $C^{-1}$ and $C^{T}$ as the inverse and the transposition of matrix $C$, respectively. The function

is of class $\mathbb{K}$ if $\digamma$ is continuous, strictly increasing, and

For some intervals

and

we define

as a continuous function and

as a continuous function everywhere except at some instant $t$, at which $\psi(t^{+})$ and $\psi(t^{-})$ exist and

For any positive sequence $\{t_{k}, k\in\mathbb{Z_{+}}\}$, denote set

where $t_{k}$ is strictly increasing and

Furthermore, for any $\mu > 0$, denote set

and

For $r > 0$, let

denote the set of piecewise right continuous functions

with the norm

Consider the following nonlinear impulsive delayed system:

where $x(t)\in\mathbb{R}^{n}$, $x_{t}\in PC_{r}$ is defined by

for $-r\leq s\leq 0$,

and

$h$ is the impulse input delay satisfying

Assume that

in this article. The function $\xi\in PC_{\chi}$ is the initial value of the system with

Given a positive constant $\mathcal{M}$, define

Assume that $f$ and $g$ satisfy some indispensable conditions (see ^[14]), and moreover,

$k\in\mathbb{Z}_{+}$, so that system (2.1) has a unique solution $x(t, t_{0}, \xi)$.

Definition 2.1. ^[3] The function

is within class $\nu_{0}$ if:

(1) $\mathbf{V}$ is continuous on every $[t_{k-1}, t_{k})\times \mathbb{R}^{n}$ and

(2) $\mathbf{V}(t, x)$ is locally Lipschitzian in $x$ and $\mathbf{V}(t, 0)\equiv 0$, $t\in\mathbb{R_{+}}$.

Definition 2.2. ^[3] For given $\mathbf{V}\in\nu_{0}$, $t\neq t_{k}$ in $\mathbb{R}_{+}$ and $\Phi\in PC_{\chi}$, define the Dini derivative of $\mathbf{V}$ along the solution of (2.1) as

Definition 2.3. ^[3] Given $\{t_{k}\}\in\mathcal{F}$ with $\mathcal{F}\subset\mathcal{F}_{0}$, system (2.1) is weakly locally exponentially stable (WLES) over class $\mathcal{F}$ with respect to $PC^{\mathcal{M}}_{\chi}$ if there exist functions $\varpi_{1}, \varpi_{2}\in\mathbb{K}$ and positive scalars

such that

implies

When

system (2.1) is locally exponentially stable (LES) over class $\mathcal{F}$ with respect to $PC^{\mathcal{M}}_{\chi}$. Furthermore, when

system (2.1) is globally exponentially stable (GES) over class $\mathcal{F}$.

Lemma 2.1. ^[30] Given matrices $\mathcal{W}_{1}$, $\mathcal{W}_{2}$, and $\mathcal{Q}$ of suitable dimensions with

for any positive constant $\varepsilon$, it holds that

Remark 2.1. Notice that in the classical theorems on exponential stability of nonlinear impulsive systems, the energy function $\mathbf{V}(x(t))$ is required as

with $\gamma > 0$ at the impulse instant, which implies that the growth or decay of the discrete dynamics is expressed in a linear form. However, such restriction on discrete dynamics is conservative. It is sometimes hard to construct an appropriate energy function for processing in practical applications. The following example can demonstrate this situation. On the other hand, as far as we know, the dual effects of delays in impulses were not investigated in the aforementioned results.

Example 2.1. Consider the following system:

where $\beta > 0$. Now we consider the energy function at the impulse time. Choose

When $t = t_{k}$,

It is noted that $\beta x((t_{k}-0.2)^{-})$ is dependent on the state of the system, so it is not possible to obtain a uniform bound such that the condition

holds. In fact, it can be found that no matter what kind of Lyapunov function we choose, due to the existence of highly nonlinear function $\beta x((t-0.2)^{-})$, the changing rate of discrete dynamics cannot be upper bounded by a linear constant. Thus the existing results are inapplicable to such a case.

Inspired by the above discussion, we will propose some new L-R theorems for system (2.1) with discrete dynamics involving both linear rate and nonlinear rate.

3.   Main results

In this section, some criteria are presented to ensure the LES of system (2.1), where two cases of delayed impulses are considered. Our first criteria indicates that the unstable system can be made locally exponentially stable under stabilizing delayed impulses.

Theorem 3.1. Assume that there exist functions $\varpi_{1}, \varpi_{2} \in \mathbb{K}$, $\mathbf{V} \in \nu_{0}$, $c \in C(\mathbb{R}_{+}, \mathbb{R}_{+})$, $m \in PC(\mathbb{R}_{+}, \mathbb{R}_{+})$, and positive constants $\eta$, $\gamma$, $\zeta$, $\alpha$, $\beta$, $q$, $\mu$, $\mathcal{M}$ with

such that for all $k \in \mathbb{Z}_{+}$:

(ⅰ) $\varpi_{1}(|x|) \leq \mathbf{V}(t, x) \leq \varpi_{2}(|x|), \ \ (t, x) \in [t_{0} - \chi, \infty) \times \mathbb{R}^{n};$

(ⅱ) $D^{+}\mathbf{V}(t, \Phi(0)) \leq m(t) c (\mathbf{V}(t, \Phi(0)))$ for every $\Phi \in PC_{\chi}$ if $e^{\eta s} \mathbf{V}(t+s, \Phi(s)) \leq \gamma \zeta \mathbf{V}(t, \Phi(0))$, $s \in [-\chi, 0]$, $t \geq t_{0}$, $t \neq t_{k};$

(ⅲ) $\mathbf{V}(t_{k}, g_{k}(y)) \leq \alpha \mathbf{V}((t_{k} - h)^{-}, y) + \beta \mathbf{V}^{q}((t_{k} - h)^{-}, y)$ for every $y \in \mathbb{R}^{n};$

(ⅳ) $(\mu - h) \cdot \sup_{t \in \mathbb{R}_{+}} m(t) \cdot \sup_{s \in \mathbb{R}_{+}} \frac{c(s)}{s} < \ln\gamma < - \ln (\alpha + \beta (\gamma \varpi_{2}(\mathcal{M}))^{q - 1}).$

Then system (2.1) is WLES over class $\mathcal{F}_{1}(\mu)$ with respect to $PC^{\mathcal{M}}_{\chi}$.

Proof. Denote

as the solution of system (2.1) through $(t_{0}, \xi)$. Define

According to condition (ⅳ), there exists a

In the following, we prove that for $k\in \mathbb{Z_{+}}$,

For convenience, define

and

First, we prove that

on $[t_{0}, t_{1}-h)$. Suppose the contrary, where there will be a $t$ such that

Set

Obviously,

Then it holds that

and

Since

and

there exists a

From the above discussion, it gives that

and

on $[t_{\vartriangle}, t^{\vartriangle}].$ Until now, we derive that

on $[t_{\vartriangle}, t^{\vartriangle}]$. Combing this with the definition of $\lambda$, one gets that, for $\forall t\in[t_{\vartriangle}, t^{\vartriangle}]$ and $s\in[-\chi, 0]$,

From (ⅱ), it yields that

on $[t_{\vartriangle}, t^{\vartriangle}].$ Thus we have that

On the other hand,

that is

which is a contradiction, implying that

on $[t_{0}, t_{1}-h).$

Next, we prove

Suppose the contrary, where there will be a $t\in[t_{1}-h, t_{1})$ such that

Let

Obviously,

Then we have that

and

Observe that

and

which indicates that there is a

From the above discussion, we have that

and

Up to now, we deduce that

Combing this with the definition of $\lambda$, it is easily checked that, for any $t\in[t_{\triangleleft}, t^{\triangleleft}]$ and $s\in[-\tau, 0]$,

It then follows from condition (ⅱ) that

Thus one can derive that

Note that

that is

which is a contradiction. So we have proven that

Next, by mathematical induction, assume that (3.1) holds for $k = 1, 2, \ldots, l$ $(l\in\mathbb{Z_{+}}, l\geq 1)$, which is equal to

From condition (ⅲ) and the definition of $\lambda$, we get

Now we prove that

on $[t_{l}, t_{l+1}-h)$. Suppose the opposite, where there will be some instant $t$ on $[t_{l}, t_{l+1}-h)$ such that

Set

Notice that

which implies that $t^{\diamond} > t_{l}$. We then have that

Note that

and

Define some constant

Similarly, we have that

and

on $(t_{\diamond}, t^{\diamond})$. So far, we have obtained that

on $[t_{\diamond}, t^{\diamond}]$. Combing this with the definition of $\lambda$, it can be easily checked that, for any $t\in[t_{\diamond}, t^{\diamond}]$ and $s\in[-\tau, 0]$,

Then we have that

Similar to (3.2), we have that

which is a contradiction. So we have proven that

on $[t_{l}, t_{l+1}-h)$.

In the following, we prove that

on $[t_{l+1}-h, t_{l+1})$. Suppose the opposite, where there will be some instant $t$ on $[t_{l+1}-h, t_{l+1})$ such that

Set

Notice that

which implies that

We then have that

Note that

and

Define some constant

Similarly, it follows that

and

on $(t_{\circ}, t^{\circ})$. So far, we have obtained that

on $[t_{\circ}, t^{\circ}]$. Combing this with the definition of $\lambda$, it can be easily checked that, for any $t\in[t_{\circ}, t^{\circ}]$ and $s\in[-\tau, 0]$,

Then we have that

Similar to (3.3), we have that

which is a contradiction. So we have proven that

on $[t_{l+1}-h, t_{l+1})$.

By mathematical induction, we get that $\vartheta(t)\leq \Omega_{2}(t)$ holds for any $k\in\mathbb{Z_{+}}$. Thus, we have that

The detailed proof is complete.□

Remark 3.1. In Theorem 3.1, condition (ⅱ) implies that the continuous dynamics of system (2.1) are unstable. Condition (ⅲ) together with condition (ⅳ) implies that discrete dynamics involving impulsive effects are stabilizing. In this case, the maximum impulsive interval satisfies

indicating that the interval between impulses should not be too large. Moreover, notice that the presence of delays in stabilizing impulses allows the maximum impulsive interval $\mu$ to exceed the case without delays (i.e., $h = 0$). In other words, the impulses can occur in less frequency, highlighting the positive influence of delays in impulses. However, as a price, the constant $\gamma$ in the Razumikhin condition is restricted to cover the delay information only on every $[t_{k-1}, t_{k}-h), k\in \mathbb{Z_{+}}$, which is not enough to deal with the delays in continuous dynamics. To this end, another parameter $\zeta$ is introduced in the Razumikhin condition to integrate the delay information on every $[t_{k}-h, t_{k}), k\in \mathbb{Z_{+}}$, to the Razumikhin condition, which is crucial to ensure the desired property of the trajectory. On the other hand, observe that due to the presence of nonlinearity in the discrete dynamics, our results are only applicable within a local framework. Therefore, estimating the initial region becomes very meaningful and the following corollary is deduced with

Corollary 3.1. Assume that there exist a function $\mathbf{V} \in \nu_{0}$ and positive constants $b_{1}$, $b_{2}$, $p$, $m$, $\eta$, $\gamma$, $\zeta$, $\alpha$, $\beta$, $q$, $\mu$ with $q > 1$, $\gamma > 1$, $\zeta > e^{mh}$ such that for all $k \in \mathbb{Z}_{+}$, condition (ⅲ) in Theorem 3.1 holds and:

(ⅰ') $b_{1}|x|^{p} \leq \mathbf{V}(t, x) \leq b_{2}|x|^{p}, \quad (t, x) \in [t_{0} - \chi, \infty) \times \mathbb{R}^{n};$

(ⅱ') $D^{+}\mathbf{V}(t, \Phi(0)) \leq m \mathbf{V}(t, \Phi(0))$ for every $\Phi \in PC_{\chi}$ if $e^{\eta s} \mathbf{V}(t+s, \Phi(s)) \leq \gamma \zeta \mathbf{V}(t, \Phi(0))$, $s \in [-\chi, 0]$, $t \geq t_{0}$, $t \neq t_{k};$

(ⅳ') $m(\mu - h) < \ln\gamma < - \ln \alpha.$

Then system (2.1) is LES over class $\mathcal{F}_{1}(\mu)$ with respect to $PC^{\mathcal{M}}_{\chi}$, where the constant $\mathcal{M}$ satisfies

In the following, the criteria on LES of system (2.1) with destabilizing delayed impulses is presented.

Theorem 3.2. Assume that there exist functions $\varpi_{1}, \varpi_{2} \in \mathbb{K}$, $\mathbf{V} \in \nu_{0}$, $c \in C(\mathbb{R}_{+}, \mathbb{R}_{+})$, $m \in PC(\mathbb{R}_{+}, \mathbb{R}_{+})$ and positive constants $\eta$, $\gamma$, $\alpha$, $\beta$, $q$, $\mu$, $\mathcal{M}$ with $q > 1$, $\gamma \geq 1$, such that for all $k \in \mathbb{Z}_{+}$:

(ⅰ) $\varpi_{1}(|x|) \leq \mathbf{V}(t, x) \leq \varpi_{2}(|x|), \quad (t, x) \in [t_{0} - \chi, \infty) \times \mathbb{R}^{n};$

(ⅱ) $D^{+}\mathbf{V}(t, \Phi(0)) \leq -m(t) c (\mathbf{V}(t, \Phi(0)))$ for every $\Phi \in PC_{\chi}$ if $e^{\eta s} \mathbf{V}(t+s, \Phi(s)) \leq \gamma \mathbf{V}(t, \Phi(0))$, $s \in [-\chi, 0]$, $t \geq t_{0}$, $t \neq t_{k};$

(ⅲ) $\mathbf{V}(t_{k}, g_{k}(y)) \leq \alpha \mathbf{V}((t_{k} - h)^{-}, y) + \beta \mathbf{V}^{q}((t_{k} - h)^{-}, y)$ for every $y \in \mathbb{R}^{n};$

(ⅳ) $\ln(\alpha + \beta (\varpi_{2}(\mathcal{M}))^{q - 1}) < \ln \gamma < (\mu - h) \cdot \inf_{t \in \mathbb{R}_{+}} m(t) \cdot \inf_{s \in \mathbb{R}_{+}} \frac{c(s)}{s}.$

Then system (2.1) is WLES over class $\mathcal{F}_{2}(\mu)$ with respect to $PC^{\mathcal{M}}_{\chi}$.

Proof. Denote

as the solution of system (2.1) through $(t_{0}, \xi)$. Define

According to condition (ⅳ), there will be a

In the following, we will show that for every $[t_{k-1}, t_{k}), k\in \mathbb{Z_{+}}$,

Set

Denote

where

Obviously,

for $t\in [t_{0}-\chi, t_{0}].$

Next, we shall prove that

First we show that

If this assertion is false, there will be an instant $t^{\ast}\in[t_{0}, t_{1})$ such that

and

Then we have that

i.e.,

which gives that

By (ⅱ), we deduce that

Thus we have that

which is a contradiction. Hence, (3.6) is true, and then

So one can derive from (ⅲ) and (ⅳ) that

By using a similar proof to (3.6), we have that

Now, we claim that

To do this, we first prove that

If

two cases are under consideration:

$(a)$ $G(t) > \varpi_{2}(|\xi|_{\chi})$ on $[t_{1}, t_{2}-h)$;

$(b)$ There will be a constant $t\in[t_{1}, t_{2}-h)$ such that $G(t)\leq \varpi_{2}(|\xi|_{\chi})$.

For the former case $(a)$, we have that

and $s\in[-\chi, 0]$, implying that

By (ⅱ) we deduce that

Thus,

Integrating the above inequality from $t_{1}$ to $t_{2}-h$, it yields that

Then

which is a contradict to the definition of $\lambda$. For case $(b)$, denote

Obviously,

and

on $[\overline{t}, t_{2}-h)$. It indicates that

i.e.,

where $s\in[-\chi, 0], \ t\in[\overline{t}, t_{2}-h)$. It then implies from (ii) that

Following a similar line of reasoning as (3.6), we have that

on $[\overline{t}, t_{2}-h)$. Then it comes to a conclusion that

which leads to a contradiction. Thus (3.8) holds. Using the similar argument in (3.6) with $t_{2}-h$ in place of $t_{0}$, one can prove that (3.7) holds. Up to now, we have that

Combing with the definition of $\lambda$, one can conclude that

Therefore, we deduce that

Based on the assertions of (3.9), in either case,

is always true for $t\geq t_{0}$. Hence,

The proof is complete.□

Remark 3.2. In Theorem 3.2, condition (ⅱ) implies that the continuous dynamics of system (2.1) are stable, while condition (ⅲ) together with condition (ⅳ) implies that discrete dynamics involving impulsive effects may be destabilizing. In this case, the minimum impulsive interval satisfies

indicating that the impulsive interval cannot be too short. Furthermore, note that the presence of delays in destabilizing impulses necessitates a larger minimum impulsive interval compared to the case without delays (i.e., $h = 0$). In other words, the impulsive disturbance should occur in less frequency, highlighting the negative influence of delays in impulses. On the other hand, the result in Theorem 3.2 is similarly derived locally, which gives the following corollary.

Corollary 3.2. Assume that there exist a function $\mathbf{V} \in \nu_{0}$, and positive constants $b_{1}$, $b_{2}$, $p$, $m$, $\eta$, $\gamma$, $\alpha$, $\beta$, $q$, $\mu$ with $q > 1$, $\gamma \geq 1$, such that for all $k \in \mathbb{Z}_{+}$, condition (ⅲ) in Theorem 3.2 holds, and:

(ⅰ') $b_{1} |x|^{p} \leq \mathbf{V}(t, x) \leq b_{2} |x|^{p}, \quad (t, x) \in [t_{0} - \chi, \infty) \times \mathbb{R}^{n};$

(ⅱ') $D^{+}\mathbf{V}(t, \Phi(0)) \leq -m \mathbf{V}(t, \Phi(0))$ for every $\Phi \in PC_{\chi}$ if $e^{\eta s} \mathbf{V}(t+s, \Phi(s)) \leq \gamma \zeta \mathbf{V}(t, \Phi(0))$, $s \in [-\chi, 0]$, $t \geq t_{0}$, $t \neq t_{k};$

(ⅳ') $\ln \alpha < \ln \gamma < m (\mu - h).$

Then system (2.1) is LES over class $\mathcal{F}_{2}(\mu)$ with respect to $PC^{\mathcal{M}}_{\chi}$, where the constant $\mathcal{M}$ satisfies

Remark 3.3. Recently, the stability issues on nonlinear systems with delayed impulses have been investigated in ^{[14,15,16,22,23,24,25,26]}. However, authors in ^[14,15,16] focused exclusively on the robustness of delays in impulses, treating delays as destabilizing factors without considering their potential stabilizing effects. On the contrary, the authors in ^[22,23,24] only addressed the positive influence of delays in impulses and ignored the negative influence. Although authors in ^[25,26] studied the dual effects of delays in impulses, they still have some limitations. The authors in ^[25] only studied the case that delays exist in impulses, neglecting the influence of delays in continuous dynamics. The authors in ^[26] considered the effects of delays in both continuous dynamics and impulses. However, the delays in continuous dynamics are all restricted to be smaller than the impulsive interval, which is conservative relatively. In this article, by employing a new Razumikhin approach, some sufficient conditions for exponential stability of systems with impulses involving dual effects of delays are presented, where the undesired restrictions of delays in continuous dynamics in ^[25,26] are completely dropped. It significantly broadens the applicability of the theoretical results.

Remark 3.4. In recent years, some exponential stability results for impulsive time-delay systems have been reported. However, a common requirement of these results is that the increase or decay of discrete dynamics is constrained by a linear rate, which limits the application of these results. In our work, the above-mentioned restriction is relaxed by fully taking the nonlinear rate in discrete dynamics into consideration, making it possible to investigate systems with highly nonlinear impulses. As far as we know, this kind of problem cannot be solved with the classical results. However, the existence of a nonlinear rate in discrete dynamics will bring some difficulties to the stability study of the systems. To solve this problem, an elastic relationship among impulses, the continuous dynamics and domain of the initial value is constructed, which is crucial to achieve the desired LES property. Furthermore, the size of the initial domain can be adjusted flexibly according to this relationship. For example, in Corollary 3.1, $\mathcal{M}$ can be made larger by reducing the values of $\alpha$ and $\beta$. That is to say, we can obtain a larger initial domain by increasing the strength of the impulsive control.

4.   Application

In this section, the established theoretical results will be employed to analyze the stability of a class of nonlinear systems. First, consider the following nonlinear impulsive time-delay system:

where

are constant matrices and

is a nonlinear function meeting the following hypotheses:

$\mathbf{(H_{1})}$ Assume that $\omega(x)$ is a vector function satisfying $|\omega_{i}(s)|\leq l_{i}|s|$, $\forall s\in \mathbb{R}$, where $l_{i} > 0$ is a constant, $i = 1, \ldots, n$. In particular, $\omega(0)\equiv 0$. Define $L = diag(l_{i})$ for later use.

$\mathbf{(H_{2})}$ For nonlinear function $G$, there exists a constant $q\geq1$ such that $|G(s)| \leq |s|^{q}$ for all $s\in\mathbb{R}^{n}$. In particular, $u(0)\equiv 0$.

Corollary 4.1. Assume that there exist positive constants $b_{1}$, $b_{2}$, $m$, $\eta$, $\gamma$, $\zeta$, $\mu$, $\varepsilon$, $\beta$ with $\gamma > 1$, $\zeta > e^{hm}$, $n\times n$ matrices $P > 0$, $Q > 0$, and $n\times n$ constant matrix $R$ such that

and

(ⅰ')$\; \begin{pmatrix} A^{T}P+PA-\nu P & \sqrt{\varepsilon}PB \\ \star & -Q \\ \end{pmatrix}$ $\leq 0$,

(ⅱ')$\; \begin{pmatrix} -\beta P & R \\ \star & -P \end{pmatrix}$ $\leq 0$,

(ⅲ')$\; (\mu-h)m < \ln\gamma,$

where

Then system (3.9) is LES over class $\mathcal{F}_{1}(\mu)$ with respect to $PC^{\mathcal{M}}_{\chi}$, where

and the impulsive control gain can be designed by

In addition, if $q = 1$, system (3.9) is GES over class $\mathcal{F}_{1}(\mu)$.

Proof. Select Lyapunov function

Obviously

Considering Lemma 2.1 and condition (ⅰ'), when

we have that for $t\in[t_{k-1}, t_{k})$, $k\in\mathbb{Z_{+}}$,

where

When $t = t_{k}$, $k\in\mathbb{Z_{+}}$, it implies from condition (ⅱ') and

that

Then by Corollary 3.1, it follows that system (3.9) is LES over class $\mathcal{F}_{1}(\mu)$ with respect to $PC^{\mathcal{M}}_{\chi}$.□

Using the similar argument to Corollary 4.2, the following corollary is derived.

Corollary 4.2. Given matrix $K$, assume that there exist positive constants $b_{1}$, $b_{2}$, $m$, $\eta$, $\gamma$, $\mu$, $\varepsilon$, $\beta$ with $\gamma\geq1$, $n\times n$ matrices $P > 0$, $Q > 0$, and $n\times n$ constant matrix $R$ such that

and

(ⅰ')$\; \begin{pmatrix} A^{T}P+PA+\nu P & \sqrt{\varepsilon}PB \\ \star & -Q \\ \end{pmatrix}$ $\leq 0$,

(ⅱ')$\; \begin{pmatrix} -\beta P & K^{T}P \\ \star & -P \end{pmatrix}$ $\leq 0$,

(ⅲ')$\; \ln\gamma < (\mu-h)m,$

where

Then system (3.9) is LES over class $\mathcal{F}_{2}(\mu)$ with respect to $PC^{\mathcal{M}}_{\chi}$, where

In addition, if $q = 1$, system (3.9) is GES over class $\mathcal{F}_{2}(\mu)$.

Remark 4.1. The stability problem for system (4.1) has been studied in ^[3,8,9,29]. Note that the above results are all on the basis of a simple assumption of the function $G$, i.e.,

In such case, the impulsive strength in condition (ⅱ') is presented by a strict restriction that

or

with $\gamma > 1$. While in Corollaries 4.1 and 4.2, such restriction between the constants $\beta$ and $\gamma$ is dropped and replaced by a more elastic implicit relationship involving $\beta$, $\gamma$, $\mathcal{M}$, $b_{1}$, $b_{2}$, and $q$. Under the same impulsive frequency, it indicates that even under the case

the impulsive effects can still be stabilizing by properly adjusting the constants $\gamma$, $\mathcal{M}$, $b_{1}$, $b_{2}$, and $q$. Conversely, when

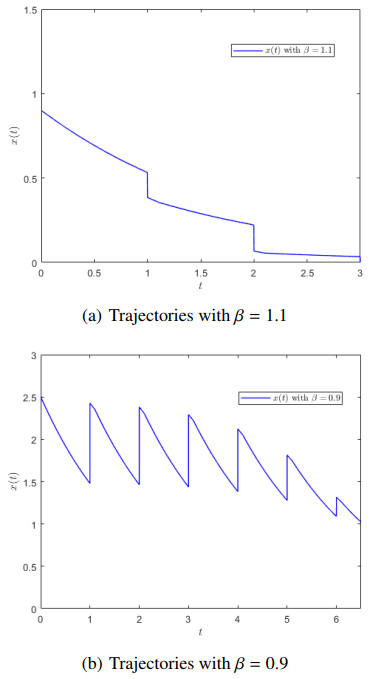
the impulses may exhibit destabilizing effects due to the highly nonlinear feature of impulses at discrete instants. Next we will recall Example 2.1 to illustrate these situations. When choose $\beta = 1.1$, Figure 1a shows that the effects of nonlinear impulses can still be stabilizing. On the contrary, choose $\beta = 0.9$, and the nonlinear impulses could exhibit destabilizing effects, which is shown in Figure 1b.

5.   Examples

Example 5.1. (Chua's oscillator ^[21]) Now we consider the classical nonlinear electronic Chua circuits. The driving system is described by

where

Take the slave system as

with $k\in \mathbb{Z_{+}}$,

for $t = t_{k}$, and $K\in \mathbb{R}^{3}$ is the impulse weight to be designed. When $\alpha = 10,$ $\beta = 16$, $m_{0} = -8/7$, $m_{1} = -5/7$, $\chi = 0.02$, and the initial function of $x(t)$ is

for $s \in [-0.02, 0]$, the trajectories of Chua's double scroll attractor without impulse input are shown in Figure 2a.

Set

as the error between systems (5.1) and (5.2). Consequently, the resulting system can be regarded as the following error system:

with

Take $h = 0.0792$. Let $m = 11.3014$, $\nu = 6$, $\eta = 0.001$, $\gamma = 1.02$, $\zeta = 2.6$, $\mu = 0.08$, $\varepsilon = 0.5$, $\beta = 0.98$, and $G(s) = s$, and the feasible solutions in Corollary 3.1 are derived by

Then system (5.3) is GES over class $\mathcal{F}_{1}(0.08)$, and the control gain matrix $K$ can be designed by

In simulations, let $t_{k} = 0.08k$, $k\in \mathbb{Z_{+}}$, and the initial function of $y(t)$ is

Then the trajectory of the error system between systems (5.1) and (5.2) is shown as the blue curve in Figure 3. Figure 2b depicts the trajectories of systems (5.1) and (5.2), which achieve exponential synchronization under the case impulses involving stabilizing delays. Under identical conditions, if $h = 0$ (i.e., there are no delays in the impulses), the red curve in Figure 3 reveals that exponential synchronization is destroyed, which shows the fact that delays in impulses could have positive influence in the synchronization of chaotic systems.

Example 5.2. Consider the following system:

where

From Figure 4a, we know that system (5.4) is stable without impulses. Consider destabilizing impulses with the form

$t_{k} = 1.5k-0.6$, $h = 0.5$, $k\in\mathbb{Z_{+}}$, $i = 1, 2$. Note that the existence of $0.4 x_{i}^{2}((t_{k}-h)^{-})$ in system (5.4) makes the GES results in ^{[26,27,28,29]} invalid. However, by Corollary 3.2, we choose

Then condition (ⅰ') holds with

Take $\gamma = 3,$ $\eta = 0.001$, and $\mu = 1.5$, whenever

one can deduce that

Thus conditions (ⅱ')–(ⅳ') are satisfied with $m = 1.1997$ and $q = 2$. According to Corollary 3.2, system (5.4) is LES over class $\mathcal{F}_{2}(1.5)$ with respect to $PC^{\mathcal{M}}_{\tau}$, where the constant $\mathcal{M}$ is estimated by

For simulations, take the initial function

To demonstrate the destabilizing effects of delays in impulses, the following different cases are considered. First, we investigate the case where the impulses are chosen as

$i = 1, 2$. As shown in Figure 4b, the destabilizing effects of impulses are relatively small, which illustrates that the stability of the system is only mildly affected by the impulses in this scenario. However, when we choose impulses with the form

$i = 1, 2,$ as indicated in Figure 4c, the impulses exhibit relative larger destabilizing effects, which shows that the presence of the delays increases the magnitude of the destabilization. Furthermore, in Figure 4d, we explore the case where the nonlinear impulses

$i = 1, 2,$ are considered. The destabilizing effects of such nonlinear impulses are considerably more significant compared to the previous cases, which emphasizes the amplifying destabilizing effects of high nonlinearity and delays in impulses on system behavior.

6.   Conclusions

Based on the Lyapunov-Razumikhin method, we investigated the LES problems of nonlinear time-delay systems with delayed impulses, focusing on both impulsive control and impulsive perturbation. Delays in impulses are shown to have dual effects: They can either destabilize a previously stable system or stabilize an otherwise unstable one. Both the linear rate and nonlinear rate in discrete dynamics are considered, where a relationship among continuous dynamics, delayed impulses, and the initial region was presented to guarantee the LES property. As applications, the stability of certain nonlinear systems with nonlinear delayed impulses was studied with the help of LMIs. Several examples have validated the efficiency of the proposed theorems. In the future, more efforts will be made to explore the average impulsive interval method to extend our proposed results.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (11501333) and Major Basic Research Program of the Natural Science Foundation of Shandong Province in China (ZR2021ZD04, ZR2020ZD24).

Conflict of interest

All authors declare no conflicts of interest in this paper.