Reachable set estimation for 2-D switched nonlinear positive systems with impulsive effects and bounded disturbances described by the Roesser model

1.   Introduction

Studies of the structure and properties of small copper and iron clusters became important because of the recent development of nanotechnologies. Moreover, the observation of changes in the atomic structure and electronic properties of clusters in relation to their size affords information on the mechanism of the transition from macroscopic to nanosized state. These nanoparticles are attractive as sensors ^[1], catalysts ^[2], nanoelectronics, and optoelectronic devices ^[3]. Their electronic, structural, magnetic, and optical properties are dramatically different from their bulk counterparts and are subject to intense investigation. With the intention of control the properties of nanoparticles through their size, their mechanism of nucleation and growth needs to be clarified, while physical properties associated with downsizing the metal nanoparticles into small nanoclusters attract attention in experimental and theoretical aspects ^[4]. A fundamental challenge for experimentalists and theorists alike is to obtain qualitative and quantitative information about the structural properties of nanoparticles that are not amenable to direct imaging.

In this regard, X-ray absorption fine structure (XAFS) analysis has proven to be a powerful qualitative and quantitative tool for structural investigations of nanoclusters. XAFS is divided into two parts, depending whether we are referring to the region near the absorption edge, which is X-ray absorption near-edge structure (XANES), or at higher energy with respect to the edge, it is extended X-ray absorption fine structure (EXAFS). XANES is now the recognized method allowing to define in principle the full 3D local atomic geometry, including symmetry and fine details of the electronic structure of the materials under study. EXAFS is a very powerful structural technique to measure the mean values of interatomic distances, coordination numbers, and static disorder. FEFF9 ^[5] is a software package which does both XANES as well as EXAFS calculations in an advanced manner. This computer code uses the real-space Green's function approach and includes improved treatments of many-body effects such as inelastic losses, core-hole effects, vibrational amplitudes, and the extension to full spectrum calculations of optical constants including solid-state effects. Each FEFF calculation involves the following 3 steps:

● Selection of the absorbing site and the cluster of atoms to be included in the scattering calculations.

● Generation of the FEFF input files for each site and its surrounding atomic cluster.

● Execution of the FEFF binary on the generated input files ^[6].

In this work, we describe the XANES and EXAFS simulation focused on the early stage of nucleation and the growth of Cu and Fe nanoparticles. Structural evolution for both Cu and Fe clusters were studied at different cluster sizes starting close to the unit cell size for each of them.

2.   Computational technique

Theoretical analysis of the Cu and Fe K-edges of absorption in the different cluster sizes was carried out based on a self-consistent real space full multiple-scattering method using FEFF9 code ^[5]. The code builds in inelastic losses in terms of a self-energy and includes vibrational effects in terms of Debye–Waller factors. For periodic structures, reciprocal space calculations based on periodic boundary conditions are also available. FEFF can use both full multiple scattering based on Lanczos algorithms and a high-order path expansion based on the Rehr–Albers multiple scattering formalism. The spectra have been simulated using several types of exchange potential: partially nonlocal potential, Hedin–Lundqvist potential and Dirac–Hara potential. Spectral dependence on the relaxation of electrons in the presence of a core hole has been studied as well. The best agreement with the experimental data has been achieved for the spectra calculated with Hedin–Lundqvist potential in the presence of core-hole. For the Cu K-edge calculation of an fcc phase, a lattice with the parameter equal to 3.61 Å ^[7] with space group Fm-3m was used. For the calculation of the Fe K-edge in the bcc phase, a lattice with the parameter equal to 2.87 Å ^[7] with space group Im-3m was used. ATOMS on the web connected to FEFF9 site was used in order to create an input file for FEFF9 program. The parameters required for ATOMS are the space group, the lattice constants, the edge of interest (Cu or Fe k-edge in the present case) and finally the central atom and cluster size. At that place there are many other parameters defined in control cards. These cards have utilized in self-consistent field that required in XANES calculation for the Fermi level estimation and full multiple scattering card that used to adjust the number of atoms used in the computation. In addition, the exchange and core hole cards which specify the exchange correlation potential model and the core treatment during calculation respectively, have applied ^[6].

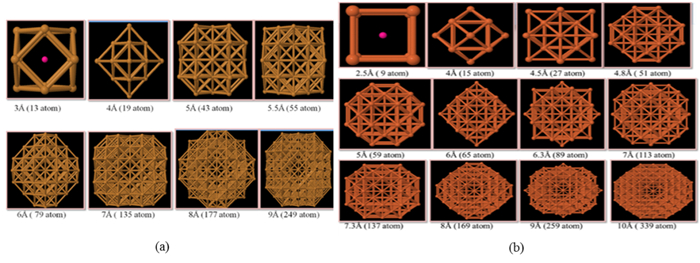
The theoretical models have constructed for metallic nanoparticles such as copper and iron at n-atoms of clusters (n = 13 to 249 atoms) for copper, and (n = 9 to 339 atoms) for iron. Then, we have carried some adjustments to the experimental reference data ^[8,9], which used in the simulation comparison. Proposed models of the copper and iron nanoclusters can be achieved when the size of the cluster changes in the diameter from 3 to 9 Å and from 2.5 to 10 Å for copper and iron respectively, as in Figure 1. Finally, extract the structural parameters and the electronic properties of metallic nanoparticles in different sizes by comparing theoretical models with reference spectra of experimental data. To extract the structural parameters such as coordination number (N), interatomic distance (R) and Debye–Waller factor (σ²) by EXAFS technique we carried out the fit procedure with experimental data as a reference by using IFEFFIT software package ^[10]. In the FEFF software, the oscillations are taken as a sum of different multiple scattering contributions. Each of them can be expressed as:

Figure 1.  Cluster models of Cu (a) and Fe (b) displaying the cluster sizes in angstrom and the number of atoms in the various shells, the absorbing atoms (shown as pink color) come along with the first models in Cu and Fe.

DownLoad: Full-Size Img PowerPoint

where, n represents different single or multiple scattering paths and ${{L_n}}$ is the total path length. F and ${{\theta _n}}$ are the amplitude and phase, which depend on k, on the specifics of the scattering path involved, and on the atomic potential parameters ^[11].

3.   Results and discussion

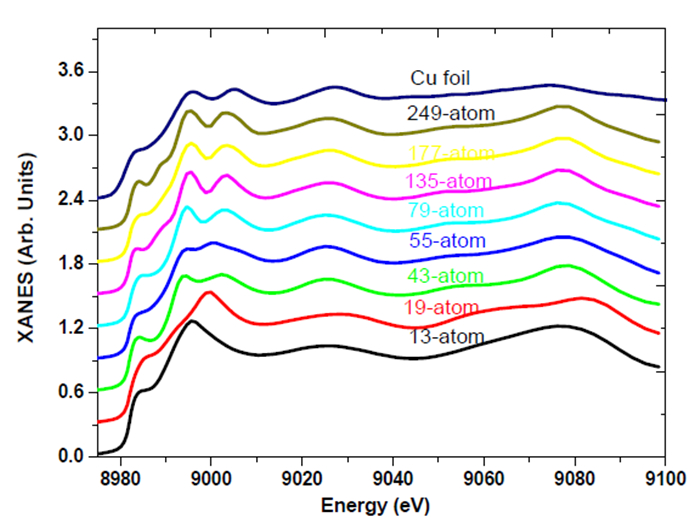
Figure 2 summarizes the calculated XANES spectra for the model n-atom clusters (n = 13–249) compared to the experimental data. The results for an fcc metal reproduce the characteristic near-edge features around 9000 eV which appear when n exceeds 43. As smaller clusters (n ≤ 19) have a single peak at this energy, the presence/absence of another peak around 9000 eV can serve as a signature of a small cluster (n ≤ 19). Focusing on small n-atom clusters (n ≤ 19), the existence of divergence observed in that curves may be because the cluster sizes (3–4 Å) are close to the lattice parameter of Cu (3.61 Å). Bazin and Rehe ^[11] have shown that the 13-atom cluster environment is not enough to produce the resonance of the second peak, and the same approach was made for a55-copper-atom cluster, where the authors considered that the features of copper K-edge are already present but with lower intensities because the surface atoms have a nonisotropic environment. It is visible that all main details of the experimental spectrum can be seen already in a cluster of 79 atoms. The further addition of atoms results only on a minor variation of relative intensities of some peaks.

Figure 2.  Calculated XANES spectra for model N-atom Cu clusters (N = 13–249) compared with experimental K-edge Cu foil ^[9].

DownLoad: Full-Size Img PowerPoint

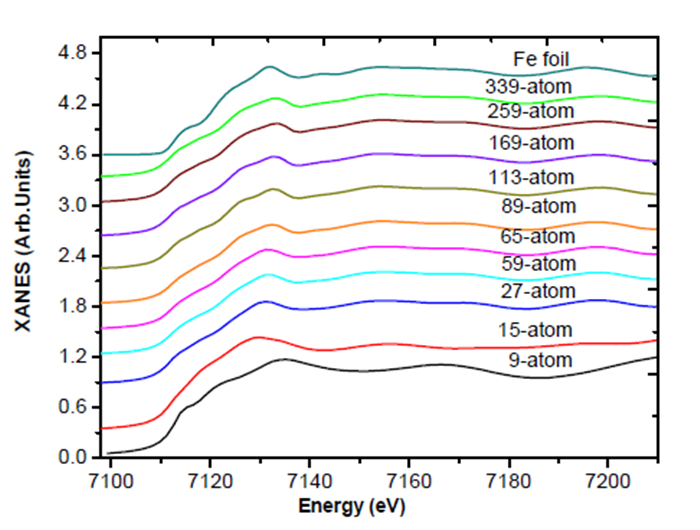
In Figure 3 the results of calculations of the Fe K-edge XANES in bcc iron for atomic clusters having different sizes are presented. From Figure 3 it can be observed that all main features of the XANES spectrum were reproduced already for a cluster containing 89 atoms. The addition of the next spheres of atoms does not result in significant changes in the spectrum. Like in Cu for small n-atoms clusters (n ≤ 27), the divergence observed in that curves may be because the cluster sizes (2.5–4.5 Å) are close to the lattice parameter of Fe (2.87 Å) or the previous interpretation of Bazin and Rehr ^[11] for copper could be applied here for iron.

Figure 3.  Calculated XANES spectra for model N-atom Fe clusters (N = 9–339) compared with experimental K-edge Fe foil ^[8].

DownLoad: Full-Size Img PowerPoint

The agreement obtained between theoretical and experimental data (Figures 1 and 2) shows that theoretical approach used in the present study works well and it is possible to apply this technique to obtain the information on local atomic structure Cu and Fe nanoparticles.

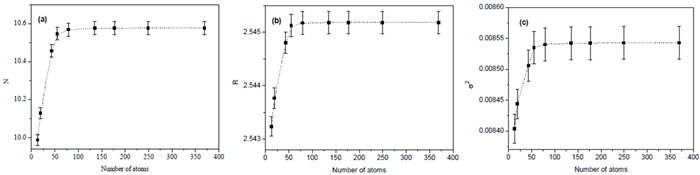
By using the EXAFS technique and fitting method for the first peak Fourier transform, it is possible to calculate the structural parameters N, R, and σ² of the first coordination shell in all proposed models. The coordination number of atoms around the absorbing atom in cluster size from 3 to 9 Å has been calculated when fitting the models with experimental data of Cu bulk, as well as interatomic distance and Debye–Waller factor. When representing the relationship between the number of atoms and the three structural parameters, it find that, increasing the number of atoms leads to rapidly increase the structural parameters until we reach the size of 5 Å (43 atoms) for Cu, after that the values of these parameters are approximately stable, as shown in Figure 4.

Figure 4.  Coordination number (a), interatomic distance (b) and Debye–Waller factor (c) for Cu K-edge.

DownLoad: Full-Size Img PowerPoint

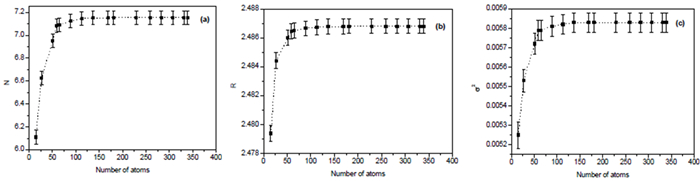
This steadiness indicates that the form of clusters began approaching the form of face-centered cubic copper crystals and arrived at stability in this form. This finding proves what has previously been achieved in the XANES spectra that have started to stability after size 5 Å (43 atoms). Figure 5 represents the relationship between the size of clusters or number of atoms and the three structural parameters for Fe. Here also the increasing of the size cluster rapidly leads to increase the structural parameters until we reach the size of 6.3 Å (89 atoms); after that, the values of these parameters are approximately stable. This stability indicates that the form of clusters began approaching the form of the body-centered cubic structure of iron crystals and arrived at stability in this form. This finding proves what has previously been achieved in the XANES spectra that have started to stability after size 6.3 Å (89 atoms).

Figure 5.  Coordination number (a), interatomic distance (b), and Debye–Waller factor (c) for Fe K-edge.

DownLoad: Full-Size Img PowerPoint

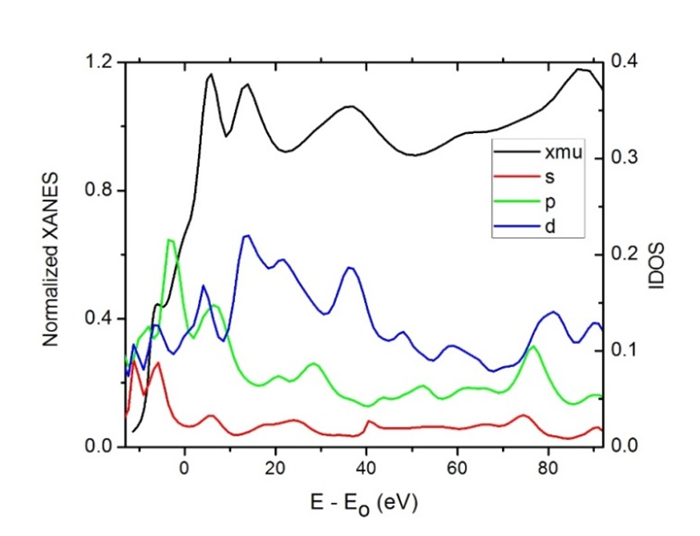
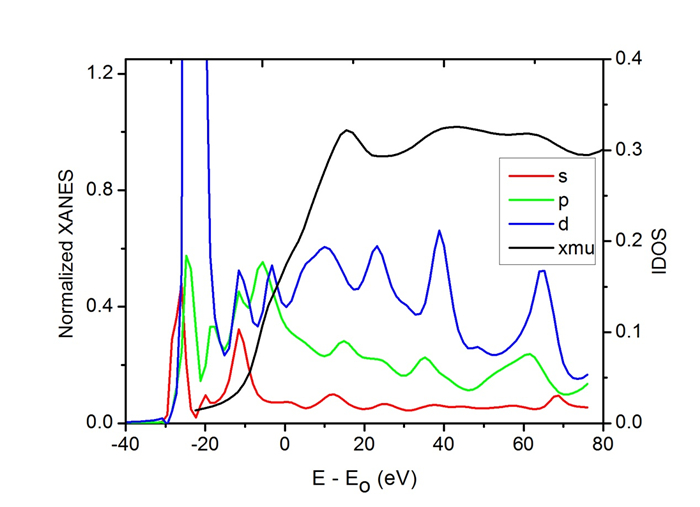
The angular momentum projected density of states (lDOS) and simulated XANES spectra of Cu cluster (135-atoms) and Fe cluster (51-atoms) are presented in Figures 5 and 6 respectively. The Figures display the density of states (s, p, and d) together with the absorption coefficient (xmu) of the normalized XANES spectra. In a metal, the Fermi level is inside one of more allowed bands. The band is partially occupied. In the semiconductor and insulating materials, the Fermi level is halfway between the conduction and valence bands ^[12]. The green line indicates the calculated local density of p states of the central copper and iron atoms in their clusters. It can be seen from Figure 6 that p-orbital contributions dominate the K absorption edge, and this is not the case for s-orbital where its maximum is observed before the edge. The absorption edge of Cu clusters almost reproduces the unoccupied band of p electrons. It is clear that the theoretically evaluated p-orbital in Figure 7 reproduces most details of the XANES particularly at the pre-edge feature of iron. The density of states for Fe appears to be due to excitation into the unoccupied p and d orbitals. Despite the 1 s→3 d transition is forbidden by dipole selection rules, the contribution of d-orbital is seen. May be the both of the 3 d + 4 p combining and the direct quadrupolar coupling is the cause for the appearing of the d-orbit ^[13].

Figure 6.  The electron DOS and the normalized XANES spectra of Cu. The Fermi level was calculated to be ca. -6.674 eV.

DownLoad: Full-Size Img PowerPoint

Figure 7.  The electron DOS and the normalized XANES spectra of Fe. The Fermi level was calculated to be ca. -17.455 eV.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

Comparing to the size-dependent XANES calculation based on a multiple scattering (MS) calculation for n-atom model clusters, it was found that the experimental XANES data are well-reproduced by a model structure consisting of 79 copper atoms and 89 iron atoms for Cu and Fe respectively. Increase the size of the clusters affects the characteristics of the structure for both Cu and Fe clusters, which was observed in the different XANES spectra at different cluster sizes. The Cu K absorption edge is dominated by p-orbital contributions. The variation of the cluster sizes influences the structural parameters such as N, R, and σ² as revealed from EXAFS results.

Conflicts of interests

All authors declare no conflicts of interest in this paper.