A new reverse Mulholland-type inequality with multi-parameters

1.   Introduction

Various modelling approaches have been proposed for the time series of counts and recent reviews on this topic can be found in many sources (^{[5,15,16,21,22,24,32,34]}). The time series of counts analysis in the literature can generally be classified into parameter-driven or observation-driven models. Zeger ^[38] initiated a class of parameter-driven models for time series of counts, which introduces autocorrelation as well as over-dispersion into the model through a latent process. Despite having wide applications in various fields, there is difficulty with efficient estimation for such parameter-driven models. Recently, Koh et al. ^[24] showed that the Monte Carlo Expectation Maximization (MCEM) algorithm is one of the alternative for the estimation of the parameters, and particle filter and smoother are useful approaches in inferencing the unobserved latent variables of the model. Jung et al. ^[21] and Jung and Tremayne ^[22] have reviewed both approaches of the parameter-driven and observation-driven models for time series of counts as well as the estimation and diagnostic tests performed for these time series models.

Observation-driven thinning-based models are commonly used to model over-dispersed or under-dispersed count data, see for example Weiß ^[33], Bourguignon and Weiß ^[3], Yang ^[37] and Kang ^[23]. Weiß ^[33] showed that the first-order nonnegative integer-value autoregressive (INAR(1)) model based on binomial thinning operator with Good- and power-law weighted Poisson-distributed innovations are particularly well-suited for modelling under-dispersed counts. Bourguignon and Weiß ^[3] proposed a new INAR(1) model for stationary count data processes with Bernoulli-geometric (BerG) marginal distributions, that can model time series of counts with over-, equi- and under-dispersion, from a new generalized thinning operator based on the convolution of binomial and negative binomial random variables. Recently, Yang ^[37] introduced a novel thinning operator based on the generalized Poisson distribution, called GP thinning operator, and Kang ^[23] defined a new thinning operator, called GSC thinning operator, based on a new discrete distribution proposed by Gómez-Déniz et al. ^[17], to construct a new INAR(1) model to capture the dispersion features of count time series count.

Another popular observation-driven approach for modelling time series of count are the INGARCH models. Heinen ^[19] proposed the autoregressive conditional Poisson (ACP) model, Ferland et al. ^[14] called it as integer-valued generalised autoregressive conditional heteroscedasticity (INGARCH) model, that has the advantage in the ease of application of the likelihood to evaluate the model. More specifically, the time series of counts $\left\{{Y}_{t}\right\}$ for $t\ge 1$ follows a conditional Poisson distribution with an autoregressive mean ${\mu }_{t}$, which is defined as

where ${\alpha }_{0} > 0$, ${\alpha }_{i}\ge 0$, ${\beta }_{j}\ge 0$, $i = \mathrm{1, 2}, \dots, p$, $j = \mathrm{1, 2}, \dots, q$, $p\ge 1, q\ge 0$ and ${\mathcal{F}}_{t-1}$ denotes the information available on the series up to and including time $t-1$. It is worth noting that the conditional mean (1.1), dependent on past observed counts and past conditional means, is similar to the conditional variance in the GARCH model by Bollerslev ^[2] as well as the conditional intensity of the autoregressive conditional duration model by Engle and Russell ^[12] for continuous-valued discrete-time data. However, the INGARCH model with Poisson distribution is suitable only for positive serial correlation and over-dispersion in the count data.

In this paper, we will focus on developing a class of observation-driven INGARCH-type models for modelling time series of counts that may exhibit over-, equi- and under-dispersion. The Poisson distribution, which has been commonly used to model time series of counts, is restrictive to the model variance equal to the mean; that is, for modelling equi-dispersed data. Therefore, Heinen ^[19] proposed the generalised double autoregressive conditional Poisson model which can model over-, equi- and under-dispersion of count time series. The double Poisson (DP) distribution proposed by Efron ^[11], which has two parameters, is used in this model. Bourguignon et al. ^[4] also used the double Poisson distribution to extend the INAR(1) for modelling count time series with over-, equi- and under-dispersion. However, Winkelmann ^[36] found that the results of the DP with its normalizing constant approximated by Efron's original method are not exact, making it a hurdle for applications. Moreover, Zhu ^[41] also argued that the DP distribution, having intractable normalizing constant and moments, is difficult to utilize for modelling and many of its properties remained unknown. Hence, some of the theoretical aspects of the resulting DP-INGARCH(1, 1) models may be difficult to establish. On the other hand, Zou et al. ^[42] noted that while DP provides a good fit when the mean is high for all dispersion types, the fit is highly unreliable when the mean is small. With these shortcomings, the DP distribution may be unattractive for the analysis of time series despite being able to model over-, equi- and under-dispersion of the count data.

Zhu ^[39] presented the negative binomial INGARCH (NB-INGARCH) model that works well for an over-dispersed poliomyelitis monthly data, and claimed that the proposed model is better than the Poisson- and DP-INGARCH models. Although the mean-variance relationship of the NB enables over-dispersion to be captured, there is difficulty in handling data characterized by under-dispersion (^[26]). Subsequently, Zhu ^[41] proposed a generalized Poisson INGARCH (GP-INGARCH) model as an alternative model to account for both over- and under-dispersion in time series of counts data. The generalized Poisson (GP) distribution has been studied extensively by many sources (^[6,7,13]). Unfortunately, Zhu ^[40] states that the GP model is not a true probability model under certain conditions, leading to its inability to model some levels of under-dispersion.

Zhu ^[40] in turn addressed the weakness of this model by proposing a COM-Poisson INGARCH model and indicating that this model is a powerful competitor to the GP model. The COM-Poisson (COMP) distribution has been proposed by Conway and Maxwell ^[8] as a model for queuing systems with state-dependent service times. This distribution has been used widely after Shmueli et al. ^[29] further examined its statistical and probabilistic properties. The COMP distribution has two parameters with λ as the centering parameter and v as the dispersion parameter. Zhu ^[40] noted that a COMP model based on the COMP formulation for λ would be difficult to interpret. To overcome this problem, a re-parameterization of the COMP distribution, $\mu = {\lambda }^{1/v}$, has been proposed by Guikema and Goffelt ^[18] to provide a clear centering parameter. Recently, Qian and Zhu ^[27] used the generalized COMP distribution, which has one more parameter than COMP distribution to handle heavy-tailed count time series.

Suitable to model both over- and under-dispersed data, the hyper-Poisson (HP) distribution is a popular distributions besides DP, GP and COMP distributions and belongs to the two-parameter family of discrete distributions. The HP distribution, introduced by Bardwell and Crow ^[1], is generated by the confluent function and admits over-dispersion as well as under-dispersion. Although the HP distribution was applied in generalized linear models and regression models for over-dispersed and under-dispersed count data (see Sáez-Castillo and Conde-Sánchez ^[28]), it is difficult to apply in INGARCH model. The mean and variance are in confluent hypergeometric form and hence, the conditional mean and conditional variance for INGARCH model are hard to derive. Kumar and Nair ^[25] then introduced an alternative hyper-Poisson (AHP) distribution, which has simpler forms of the mean and variance.

In this paper, we introduce the AHP distribution as an INGARCH model for modelling over-dispersed and under-dispersed count time series data, and then compare it to existing INGARCH models. The AHP distribution has simpler forms for the mean and variance compared to the HP distribution, making it potentially more viable and useful choice as an INGARCH model. We also investigate the properties of the AHP distribution and derive a lower bound for one of the parameters to ensure a valid probability mass function (pmf) for the case of under-dispersion. Similar to Weiß ^[31], we provide a set of Yule-Walker type equations from which the autocorrelation function of general AHP-INGARCH($p, q$) models can be obtained. In particular, we derive the equations of variance and autocorrelation function for AHP-INGARCH(1, 1) model. It is worth to noting that the unconditional variance of AHP-INGARCH(1, 1) model is more general than the unconditional variance of INGARCH model of Weiß ^[31]. The INGARCH model of Weiß ^[31] is a special case of AHP-INGARCH model when $\gamma = 1$. In the applications to three real-life data sets, we have included five existing INGARCH models, namely the Poisson-, NB-, COMP-, GP- and DP-INGARCH models in direct comparison against the proposed AHP-INGARCH model, highlighting the usefulness of AHP-INGARCH as a competitive model in practice.

The contents of this paper are organized as follows. Section 2 presents the AHP distribution along with its basic properties, while Section 3 outlines the proposed INGARCH model with the AHP distribution. The maximum likelihood estimation for the proposed model is briefly discussed in Section 4, followed by a simulation study to assess the performance of this estimation method in Section 5. Section 6 demonstrates the application of the proposed model to three real-life data sets, which exhibit different types of dispersions, in comparison to some existing models for time series of counts. Finally, Section 7 provides some concluding remarks.

2.   Some properties of the alternative hyper-Poisson distribution

In this section, we give a brief review of the hyper-Poisson (HP) distribution and its alternative form. The two-parameter HP distribution is first introduced by Bardwell and Crow ^[1] through the following probability generating function (pgf):

where $\phi \left(\mathrm{a}; b;c\right) = \sum _{k = 0}^{\mathrm{\infty }}\frac{{\left(\mathrm{a}\right)}_{k}{c}^{k}}{{\left(b\right)}_{k}k!}$ is the confluent hypergeometric series, or known as the Kummer M function, in which ${\left(a\right)}_{k} = \frac{\mathrm{\Gamma }\left(a+k\right)}{\mathrm{\Gamma }\left(a\right)}$ is the Pochhammer symbol and $\mathrm{\Gamma }\left(\bullet \right)$ is a gamma function. Sáez-Castillo and Conde-Sánchez ^[28] utilize the HP distribution to model over-dispersed and under-dispersed count data and showed that the range of values of the dispersion index of HP distribution is wide in both situations of over- and under-dispersion. However, the mean of HP distribution can only be expressed in term of the confluent hypergeometric series.

Kumar and Nair ^[25] then introduced an alternative form of HP distribution, called AHP. The pmf and pgf of AHP distribution ($AHP\left(\theta, \gamma \right))$ can be written, respectively as

and

where $Z$ is the AHP distributed random variable. Note that when $\gamma = 1$, we have $G\left(u\right) = \sum _{k = 0}^{\mathrm{\infty }}\frac{{\left[\theta \left(u-1\right)\right]}^{k}}{k!} = {e}^{\theta \left(u-1\right)}$, the pgf of a Poisson distribution with parameter $\theta$.

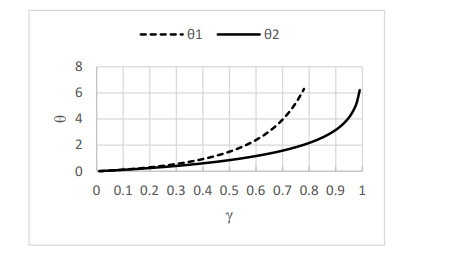
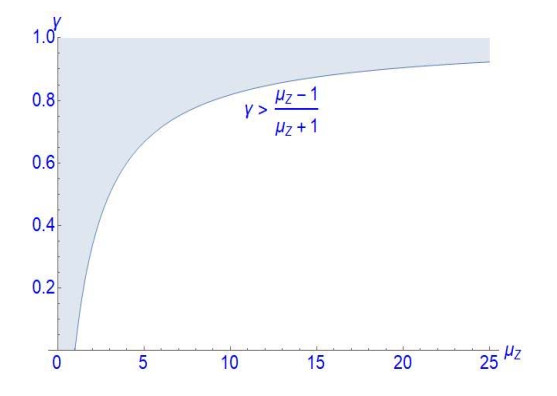
The mean and variance of a AHP distributed random variable $Z$ are, respectively, ${\mu }_{Z} = E\left[Z\right] = \frac{\theta }{\gamma }$ and ${\sigma }_{Z}^{2} = \frac{\theta }{\gamma }\left[1+\frac{\theta }{\gamma }\left(\frac{\gamma -1}{\gamma +1}\right)\right] = {\mu }_{Z}-{\mu }_{Z}^{2}+\frac{2\gamma {\mu }_{Z}^{2}}{1+\gamma }$. However, we found that in order to guarantee the positivity of the variance, the parameter $\gamma$ needs to be constrained by $\gamma > \frac{-1-\theta +\sqrt{{\theta }^{2}+6\theta +1}}{2}$ (or $\gamma > \frac{{\mu }_{Z}-1}{{\mu }_{Z}+1}$). Figure 1 shows the feasible range of $\gamma$ for a given ${\mu }_{Z}$; we note that large $\gamma$ is required for large ${\mu }_{Z}$ so that ${\sigma }_{Z}^{2} > 0$.

The parameter constraint for the positivity of the variance can also be rewritten as $\theta < {\theta }_{1}$, for $0 < \gamma < 1$, where ${\theta }_{1} = \frac{\gamma (\gamma +1)}{1-\gamma }$. However, in order to guarantee the positivity of the pmf of AHP distribution, the parameter $\theta$ needs to be constrained by $\theta < {\theta }_{2}$, where ${\theta }_{2}$ is the solution of $\phi \left(\gamma -1;\gamma; {\theta }_{2}\right) = 0$ (see Appendix A.1 for the poof). Figure 2 shows the boundary lines of ${\theta }_{1}$ and ${\theta }_{2}$ for a given $\gamma \in \left(\mathrm{0, 1}\right)$. For an AHP distribution, the feasible region of $\theta$ for a given $\gamma \in \left(\mathrm{0, 1}\right)$ is the region below the solid line in Figure 2.

The dispersion index of AHP distribution is given by

We note that the AHP distribution is under-dispersed $\left(0 < {I}_{Z} < 1\right)$ when $\frac{-1-\theta +\sqrt{{\theta }^{2}+6\theta +1}}{2} < \gamma < 1$, equi-dispersed $\left({I}_{Z} = 1\right)$ when $\gamma = 1,$ and over-dispersed $\left({I}_{Z} > 1\right)$ when $\gamma > 1$. Hence, the parameter $\gamma$ is the dispersion parameter for AHP distribution. Bourguignon and Weiß ^[3] studied the dispersion behaviour of a BerG distribution, that is, the distribution of the convolution of a Bernoulli and a geometric random variable. They found that the BerG distribution can be used in count time series modelling with over-, equi- and under-dispersion. As noted by Bourguignon and Weiß ^[3], there is no feasible region for under-dispersion when the mean is larger than two for a BerG distribution. However, the AHP distribution can be seen to cover a wider range of dispersion regions compared to the BerG distribution.

In addition, the third and fourth central moments of an AHP random variable $Z$ are obtained as follows:

3.   The AHP-INGARCH(p, q) model

Let $\left\{{\left.{Y}_{t}\right\}}_{t\ge 1}\right.$ denotes a univariate time series of counts and ${\mathcal{F}}_{t-1}$ be the $\sigma$ -field generated by $\left\{\left.{Y}_{t-1}, {Y}_{t-2}, \dots \right\}\right.$. We assume that process $\left\{{Y}_{t}\right\}$ is conditionally independent given ${\mathcal{F}}_{t-1}$ and the conditional distribution of ${Y}_{t}$ given ${\mathcal{F}}_{t-1}$ is specified by an AHP distribution, that is

where ${\alpha }_{0} > 0, {\alpha }_{i}\ge 0, {\beta }_{j}\ge 0,$ $i = 1, \dots, p$, $j = 1, \dots, q$, $p\ge 1$, $q\ge 0$, and $\gamma > 0$. This model is denoted by AHP-INGARCH(p, q). Since the conditional distribution of ${Y}_{t}$ given ${\mathcal{F}}_{t-1}$ is specified by an AHP distribution, this model will be able to account for equi- ($\gamma = 1$), over- ($\gamma > 1$) and under-dispersion ($\frac{-1-{\theta }_{t}+\sqrt{{\theta }_{t}^{2}+6{\theta }_{t}+1}}{2} < \gamma < 1$). When $\gamma = 1$, the model (3.1) is equal to the Poisson-INGARCH model introduced by Heinen ^[19] and Ferland et al. ^[14] Some of the important properties of the AHP-INGARCH(p, q) time series model are given next.

Theorem 3.1. Let $\left\{{Y}_{t}\right\}$ be a weakly stationary process with range $\left\{\mathrm{0, 1}, \dots \right\}$ following the AHP-INGARCH(p, q) model in (3.1). If $\sum _{i = 1}^{p}{\alpha }_{i}+\sum _{j = 1}^{q}{\beta }_{j} < 1$ , then

(ⅰ) the unconditional expectation of ${Y}_{t}$ is given by

(ⅱ) the covariance Cov $\left[{Y}_{t}, {\mu }_{t-k}\right]$ fulfills

(ⅲ) the autocovariances ${\gamma }_{Y}\left(k\right) = Cov\left[{Y}_{t}, {Y}_{t-k}\right]$ and ${\gamma }_{\mu }\left(k\right) = Cov\left[{\mu }_{t}, {\mu }_{t-k}\right]$ will satisfy the following equations:

The proof of Theorem 3.1 is provided in Appendix A.2.

From (3.1), the conditional mean and conditional variance of ${Y}_{t}$ are given by, respectively,

and

Then, the unconditional mean and unconditional variance of ${Y}_{t}$ are, respectively,

and

3.1.   AHP-INGARCH(1, 1) model

Consider the special case of an AHP-INGARCH(1, 1) model. With arguments similar to those in Example 1 of Weiß ^[31], we obtain the unconditional variance of the AHP-INGARCH(1, 1) model as

with the variance of the conditional mean given by $V\left({\mu }_{t}\right) = \frac{{\alpha }_{1}^{2}{\mu }_{Y}\left(\gamma +1\right)+{\alpha }_{1}^{2}{\mu }_{Y}^{2}\left(\gamma -1\right)}{\left(\gamma +1\right)\left({1-\beta }_{1}^{2}-2{\alpha }_{1}{\beta }_{1}\right)-2{\gamma \alpha }_{1}^{2}}$.

The autocovariance is

giving the autocorrelations as

The proof of this special case is provided in Appendix A.3.

Corollary 3.1. Suppose that $\left\{{Y}_{t}\right\}$ following the AHP-INARCH $\left(p\right)$ model with $q = 0$ in model (3.1) is second-order stationary, then the autocovariance function ${\gamma }_{Y}\left(k\right)$ satisfies the equation

3.2.   AHP-INARCH(1) model

Consider the AHP-INARCH(1) model. The unconditional mean and unconditional variance are given by respectively,

and

From Corollary 3.1, one immediately obtains the autocovariance function of the AHP-INARCH(1) model as

Hence, the autocorrelation function of the AHP-INARCH(1) model is

like in the standard AR(1) case.

4.   Maximum likelihood estimation

In this section, we will discuss the maximum likelihood estimation (MLE) for the AHP-INGARCH (p, q) model (3.1), that is

Let $\boldsymbol{\alpha } = {\left({\alpha }_{1}, \dots, {\alpha }_{p}\right)}^{T}, \boldsymbol{\beta } = {\left({\beta }_{1}, \dots, {\beta }_{q}\right)}^{T},$ ${\boldsymbol{\lambda }}^{*} = {\left({\alpha }_{0}, {\boldsymbol{\alpha }}^{T}, {\boldsymbol{\beta }}^{T}\right)}^{T},$ $\boldsymbol{\lambda } = {\left(\gamma, {\boldsymbol{\lambda }}^{*{\rm T}}\right)}^{T},$ and write the true value of $\boldsymbol{\lambda }$ as ${\boldsymbol{\lambda }}^{0}$. Suppose that the observation $\mathbf{Y} = \left({Y}_{1}, \dots, {Y}_{n}\right)$ is fitted with the model (3.1). The conditional likelihood function at time t is

where ${\theta }_{t} = \gamma {\alpha }_{0}+\gamma {\sum }_{i = 1}^{p}{\alpha }_{i}{Y}_{t-i}+{\sum }_{j = 1}^{q}{\beta }_{j}{\theta }_{t-j}$. The conditional log-likelihood function is

where $h\left({\theta }_{t}\right) = \mathrm{ln}\left[\phi \left(1+{Y}_{t}; \gamma +{Y}_{t}; -{\theta }_{t}\right)\right]$. The score function is defined by

with

where $\psi \left(x\right) = \frac{\partial }{\partial x}\left[\mathrm{ln}\mathrm{\Gamma }\left(x\right)\right] = \frac{1}{\mathrm{\Gamma }\left(x\right)}\frac{\partial }{\partial x}\left[\mathrm{\Gamma }\left(x\right)\right]$ is the digamma function (^[20]). The solution of the equation $\frac{\partial l\left(\boldsymbol{\lambda }\right)}{\partial \boldsymbol{\lambda }} = 0$, if it exists, gives the conditional MLE of $\boldsymbol{\lambda }$, denoted by $\widehat{\boldsymbol{\lambda }}$.

The Hessian matrix is given by

with

where ${\psi }^{{{'}}}\left(x\right) = \frac{\partial }{\partial x}\left[\psi \left(x\right)\right]$ is the trigamma function. According to White ^[35], the standard errors of $\widehat{\boldsymbol{\lambda }}$ can be computed from the robust sandwich matrix ${H}_{n}^{-1}\left(\widehat{\boldsymbol{\lambda }}\right){S}_{n}\left(\widehat{\boldsymbol{\lambda }}\right){H}_{n}^{-1}\left(\widehat{\boldsymbol{\lambda }}\right)$, where ${S}_{n}\left(\boldsymbol{\lambda }\right) = \sum _{t = 2}^{n}\frac{\partial \mathrm{ln}{l}_{t}\left(\boldsymbol{\lambda }\right)}{\partial \boldsymbol{\lambda }}\frac{\partial \mathrm{ln}{l}_{t}\left(\boldsymbol{\lambda }\right)}{\partial {\boldsymbol{\lambda }}^{T}}$, and ${H}_{n}\left(\boldsymbol{\lambda }\right) = -\sum _{t = 2}^{n}\frac{{\partial }^{2}\mathrm{ln}{l}_{t}\left(\boldsymbol{\lambda }\right)}{\partial \boldsymbol{\lambda }\partial {\boldsymbol{\lambda }}^{T}}$.

5.   Monte Carlo simulation study

Since the autocorrelation function of AHP-INGARCH(1, 1) model is derived, the parameter of AHP-INGARCH(1, 1) model can also be estimated according to the Yule-Walker approach. It is of interest to compare the efficiency of the Yule-Walker (YW) estimator with the maximum likelihood (ML) estimator. In this section, we conduct a Monte Carlo simulation study to investigate the performance of the YW and ML estimators for the proposed AHP-INGARCH(1, 1) model. The simulations are computed by using the R programming language. The data set ${Y}_{1}, {Y}_{2}, \dots, {Y}_{n}$ is generated in accordance to model (3.1) for different sample sizes $n$ and different parameter values. Due to space constraints, we showed only the simulation results for the data with fixed mean equal to one and parameters ${(\alpha }_{0} = 0.6, {\alpha }_{1} = 0.3, {\beta }_{1} = 0.1)$ for several sample sizes ($n = 100, 200\;\; \mathrm{a}\mathrm{n}\mathrm{d}\;\; 500)$ with over-dispersion $\left(\gamma = 2\right)$, equi-dispersion $\left(\gamma = 1\right)$ and under-dispersion $\left(\gamma = 0.8\right)$ in Table 1. Similar results are obtained for other sets of parameter values considered. The parameter estimates and mean square errors for the parameters ${(\alpha }_{0}, {\alpha }_{1}, {\beta }_{1}, \gamma)$ are computed over 1000 replications. In the MLE estimation, we use sample mean as the initial mean value, namely ${\mu }_{1} = \frac{1}{n}{\sum }_{i = 1}^{n}{Y}_{i}$.

Based on the results from the simulation study, the parameter estimates approach the true values along with small mean square errors at all three types of dispersions as the sample size increases.

6.   Comparison of INGARCH models

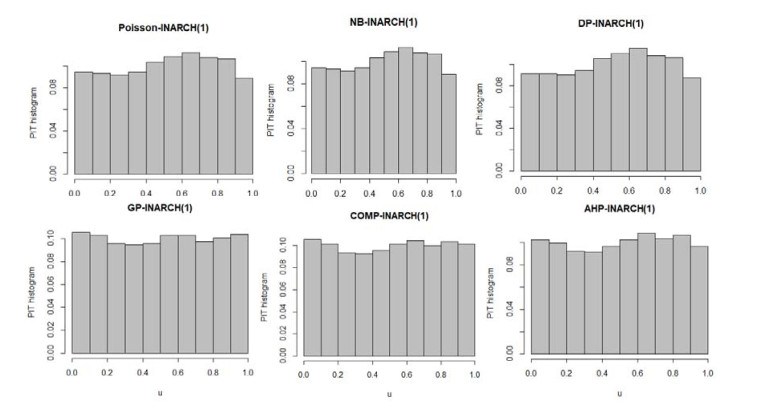
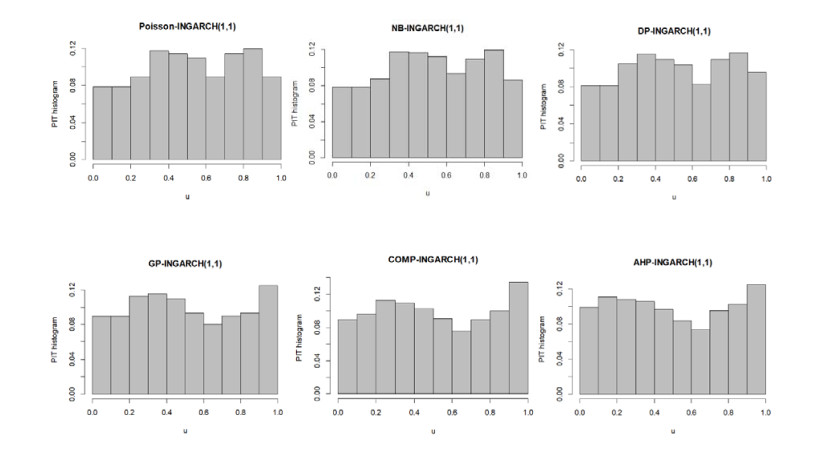
This section describes the analysis of three real-life data sets fitted by the Poisson, NB, DP, GP, COMP, and AHP distributed INGARCH-type modes. Based on the sample mean and variance, the first data set exhibits over-dispersion and the last two data sets exhibit under-dispersion. The MLE results are obtained using the R software through the Box constraints optimization (L-BFGS-B) function with the initial conditional mean equals to the sample mean. Statistical consistency between the predictive and observed distributions is investigated by plotting the histogram of probability integral transform (PIT) (see, Dawid ^[10]). According to Czado et al. ^[9], from the PIT histogram, under-dispersed predictive distribution is signified by a U-shaped histogram whereas over-dispersed predictive distribution is indicated by a hump or inverse-U shaped histogram. When central tendencies are biased, a skewed histogram is observed.

6.1.   Polio series

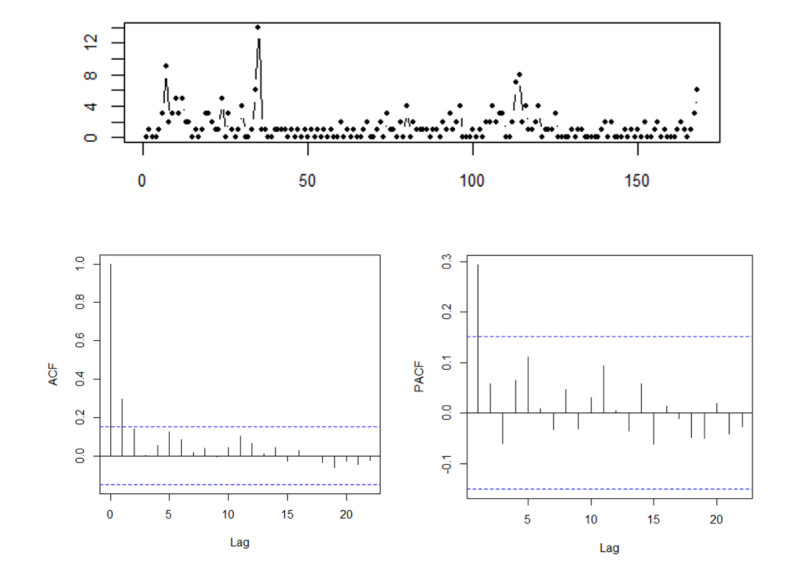
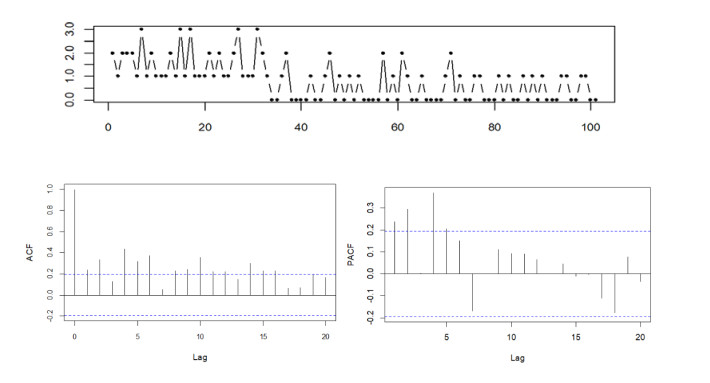
The polio data is a time series of length 168, which has been fitted by Zhu ^[39] using the NB-INGARCH model. The data series is the monthly number of cases of poliomyelitis reported by the U.S. Centers for Disease Control from 1970 to 1983 with a sample mean of 1.33 and a sample variance of 3.50. These statistics indicate that the series is over-dispersed and the sample first-order autocorrelation coefficient (FOAC), $\widehat{\rho }\left(1\right) = 0.2948$.

Figure 3 describes the original data, autocorrelation function (ACF) and partial autocorrelation function (PACF) of the polio series while Table 2 summarizes the result of six fitted INGARCH(1, 1) models.

Based on the Akaike information criterion (AIC) and Bayesian information criterion (BIC) for all the models, the AHP-INGARCH(1, 1) model is found to be comparable to the NB-INGARCH(1, 1) but better than the Poisson, DP-, GP- and COMP-INGARCH(1, 1) models for this over-dispersed polio dataset. It is worth noting that the values of the parameter estimates for NB-INGARCH(1, 1) model are different from Zhu ^[39] because they fixed the parameter $r = 2$.

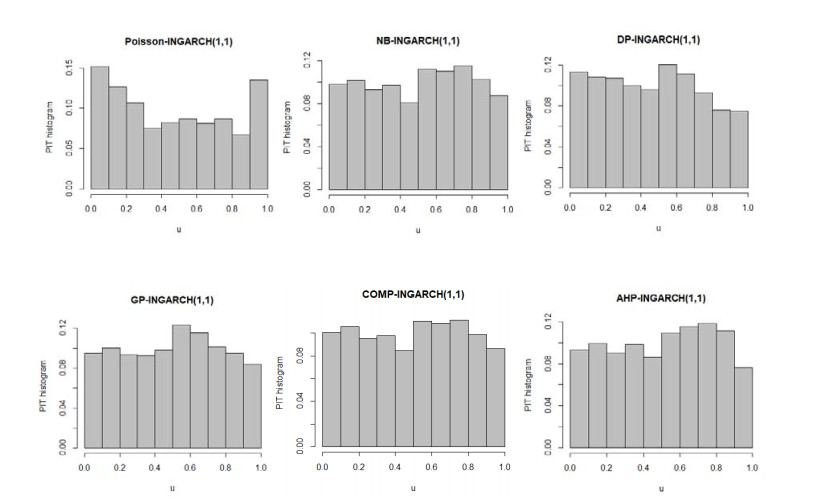
Figure 4 shows the PIT histogram of the six INGARCH(1, 1) models. Overall, Poisson-INGARCH(1, 1) model have a U-shaped histogram while DP-INGARCH(1, 1) model has a skewed histogram. Although not uniform, the NB-, GP-, COMP- and AHP-INGARCH(1, 1) have only a slight hump in the histogram indicating better performance than the Poisson- and DP-INGARCH(1, 1) models.

Comparison of the estimated means, variances, dispersion index and FOACs within the fitted Poisson, NB, DP, GP, COMP and AHP models for polio data and another two under-dispersion data sets that will be discussed later in the next sections are summarized in Table 3. The dispersion index for NB- and AHP-INGARCH(1, 1) models are closest to the dispersion index for the polio data compared to the Poisson-, DP-, GP- and COMP-INGARCH(1, 1) models.

6.2.   Internet Protocol (IP) count series

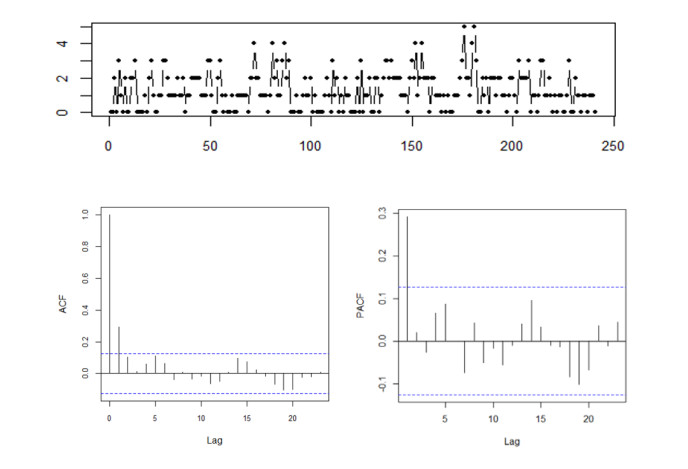
The IP counts data is a time series of length 241 that gives the number of different IP addresses registered within periods of 2-min length at the server of the Department of Statistics of the University of W $\ddot{u}$ rzburg in 29 November 2005 between 10 a.m and 6 p.m. This data set has been investigated by Weiß ^[30] and Zhu ^[40,41]. The data examined is under-dispersed since the variance (1.2052) is smaller than the mean (1.2863) with the sample FOAC of 0.2925. Figure 5 presents the IP counts time series, ACF and PACF, respectively.

Zhu ^[41] fitted the Poisson INAR(1), the Poisson-, DP- and GP- INARCH(1) and INGARCH(1, 1) models to the data and claimed that the GP-INARCH(1) model is more appropriate for this time series. Comparison of existing INARCH(1) and AHP-INARCH(1) models are summarized in Table 4. It is worth noting that the over-dispersed NB-INARCH(1) model of Zhu ^[39] is added in our analysis for comparison. As seen from Table 4, the estimated value of the NB-INARCH(1) parameter $\widehat{r}$ is large and significant, but unreliable. This is because the differentiation of the likelihood function with respect to the parameter $r$ is problematic as reported in Zhu ^[39]. We obtain the same conclusion as Zhu ^[40], that is, (ⅰ) the estimated dispersion index of GP-, COMP- and AHP-INARCH(1) models are less than 1, which indicate that the data set is under-dispersed count time series, and Poisson-, DP- and NB- INARCH(1) models wrongly indicate that the data set is over-dispersed; (ⅱ) GP model performs better in AIC and Poisson INARCH(1) performs better in BIC, but the difference of AIC and BIC values between other models are rather small. Typically, a difference in AIC value less than 2 is considered not significant (Zhu ^[40]). Based on Figure 6, the PIT histogram of the AHP, GP and COMP models shows approximate uniformity, while Poisson-, NB- and DP-INARCH(1) are slightly hump-shaped.

6.3.   COVID-19 series

The COVID-19 data is a time series of length 101 that gives the number of daily COVID-19 new deaths recorded in Saudi Arabia between 26^th January 2023 to 6^th May 2023. This data is publicly available at the website https://ourworldindata.org/. The data examined is under-dispersed since the variance (0.7347) is smaller than the mean (0.8416) with the sample FOAC of 0.2374. Figure 7 presents the COVID-19 new deaths time series, ACF and PACF, respectively.

Table 5 summarizes the results of six INGARCH(1, 1) models for the COVID-19 new deaths data. Based on AIC and BIC, the AHP-INGARCH(1-1) model is the best. The estimated value of the NB-INGARCH(1, 1) parameter $\widehat{r}$ is again large and significant, but unreliable. Besides the over-dispersed Poisson- and NB-INGARCH(1, 1) models, the dispersion index of DP-, GP-, COMP- and AHP-INGARCH(1, 1) are all less than 1 which indicate that these models are capable of capturing under-dispersed feature from the empirical data (see Table 3). All the PIT histrograms in Figure 8 visibly deviate from uniformity (with a slight preference for the AHP-INGARCH(1, 1) model). In particular, the PIT histrograms of Poisson-, NB- and DP-INGARCH(1, 1) models are slightly hump-shaped while GP-, COMP- and AHP-INGARCH(1, 1) models are slightly U-shaped.

7.   Conclusions

This work introduces a new family of AHP-INGARCH models for analysing over-dispersed and under-dispersed count time series data. The advantages of the AHP-INGARCH-type model are (ⅰ) the ease in obtaining the model mean and variance compared to distributions like the COMP and DP distributions, making the AHP distribution a useful choice for an INGARCH model, and (ⅱ) the ability to accommodate a wider range of dispersion, placing the AHP distribution as a flexible model for applications. The application of the AHP-INGARCH models to three real-life data sets clearly demonstrates the model competitiveness in studying both over-dispersed and under-dispersed data. Since $\gamma$ is the dispersion parameter of AHP distribution, one of the potential future research is to relax the assumption of constant dispersion by allowing time-varying dispersion. Another direction of future research is to extend the results to multivariate cases.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

The authors would like to thank the editor and the referees for their valuable comments.

Seng Huat Ong is supported by the Ministry of Higher Education grant FRGS/1/2020/STG06/SYUC/02/1 and UCSI University grant REIG-FBM-2022/050. The authors would like to thank INTI International University for funding the publication of this work.

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendix A

A.1.   Parameter constraint of AHP distribution

Let $Z\sim AHP\left(\theta, \gamma \right)$. The probability mass function of $Z$ can be written as

where the second equality is obtained from Johnson et al. ^[20]. Since $\frac{{\theta }^{z}{e}^{-\theta }}{{\left(\gamma \right)}_{z}} > 0$ for $\theta > 0$ and $\gamma > 0$. The positivity of the pmf of $Z$ depends on the confluent hypergeometric function

It is easy to see that $\phi \left(\gamma -1;\gamma +z; \theta \right) > 0$ when $\gamma \ge 1$. Hence, the positivity of the pmf of $Z$ is guaranteed for $\gamma \ge 1$.

For $0 < \gamma < 1$, we note that ${\left(\gamma +z\right)}_{k}\ge {\left(\gamma \right)}_{k}$ for all $z\ge 0$ and $k\ge 0.$ Since

we have

for all $z\ge 1$. Thus, for $0 < \gamma < 1$, the positivity of the pmf of $Z$ is guaranteed as long as $P\left(Z = 0\right) > 0$. This condition can be further simplified as

It is worth to note that the confluent hypergeometric function $\phi \left(\gamma -1;\gamma; \theta \right)$ is a decreasing function on $\theta$. Hence, for a given $\gamma \in \left(\mathrm{0, 1}\right)$, $\phi \left(\gamma -1;\gamma; \theta \right) > 0$ iff $\theta < {\theta }^{*}$, where ${\theta }^{*}$ is the solution of $\phi \left(\gamma -1;\gamma; {\theta }^{*}\right) = 0$.

A.2.   Proof of Theorem 3.1

(ⅰ) Let ${\mu }_{Y} = E\left[{Y}_{t}\right]$ denote the unconditional expectation of ${Y}_{t}$ if it exists. Then by the tower property of conditional expectation, we have

where $E\left[{\mu }_{t-j}\right] = E\left[E\left[{Y}_{t-j}|{\mathcal{F}}_{t-j-1}\right]\right] = {\mu }_{Y}$ by the tower property of conditional expectation.

(ⅱ) By the definition of covariance and the tower property, we have

for $k\ge 0$, where ${\mu }_{t}$ is ${\mathcal{F}}_{t-1}$ measurable, i.e, $E\left[{\mu }_{t}|{\mathcal{F}}_{t-1}\right] = {\mu }_{t}.$ The proof is completed by noticing that

For $k < 0$, by the same argument, we have

Again, we use the property that ${\mu }_{t-k}$ is ${\mathcal{F}}_{t-k-1}$ measurable, i.e., $E\left[{\mu }_{t-k}|{\mathcal{F}}_{t-k-1}\right] = {\mu }_{t-k}$ and $E\left[{Y}_{t-k}\left|{\mathcal{F}}_{t-k-1}\right.\right] = {\mu }_{t-k}$. The proof is completed by noticing that

(ⅲ) Finally, applying part (ⅱ), we have for $k\ge 0,$

Again, applying part (ⅱ), we obtain for $k\ge 1$,

A.3.   Proof of Special Case AHP-INGARCH(1, 1)

(ⅰ) Unconditional variance

From Eq (3.2), we obtain for $k\ge 2$ that

${\gamma }_{Y}\left(k\right) = {\alpha }_{1}{\gamma }_{Y}\left(k-1\right)+{\beta }_{1}{\gamma }_{Y}\left(k-1\right) = {\left({\alpha }_{1}+{\beta }_{1}\right)}^{k-1}{\gamma }_{Y}\left(1\right).$ (*)

Again, from Eq (3.2), for $k = 1$, we have

To determine an expression for $V\left({\mu }_{t}\right)$, note first that for $k\ge 1$, Eq (3.3) can be written as

For $k = 0$, Eq (3.3) can be written as

Therefore, the unconditional variance of ${Y}_{t}$ can be obtained from

(ⅱ) Autocovariance function

Given that $V\left({\mu }_{t}\right) = \frac{{\alpha }_{1}^{2}{\mu }_{Y}\left(\gamma +1\right)+{\alpha }_{1}^{2}{\mu }_{Y}^{2}\left(\gamma -1\right)}{\left(\gamma +1\right)\left({1-\beta }_{1}^{2}-2{\alpha }_{1}{\beta }_{1}\right)-2{\gamma \alpha }_{1}^{2}} = \frac{{\alpha }_{1}\left(\gamma +1\right)\left({\alpha }_{1}{\mu }_{Y}+{\alpha }_{1}{\mu }_{Y}^{2}\frac{\left(\gamma -1\right)}{\left(\gamma +1\right)}\right)}{\left(\gamma +1\right)\left({1-\beta }_{1}^{2}-2{\alpha }_{1}{\beta }_{1}\right)-2{\gamma \alpha }_{1}^{2}}$ and from Eqs (*) and (**), we obtain for $k\ge 2$ that

Note that for $k = 1$, we have