Estimating fixed points of non-expansive mappings with an application

1.   Introduction

The fixed point theory is an important and fascinating branch of mathematics. From the last century, it becomes not only a field with great development but also a strong tool for solving different kinds of problems in several fields of pure and applied mathematics. Fixed point theory is a beautiful mixture of analysis, topology, and geometry and also serves as a bridge between pure and applied mathematics besides facilitating a very fruitful area of intersection between the two. The metric fixed point theory was initiated by the Polish mathematician S. Banach in 1922. He proved a very eminent and useful result known as Banach contraction principle which stated as "Every contraction on a complete metric space has a unique fixed point". Since the applications of Banach contraction principle are restricted to only contraction mappings. Therefore we need some appropriate and nice nonlinear mappings.

Throughout this paper, $\mathbb{Z_{+}}$ denotes the set of all nonnegative integers and $\mathbb{R_{+}}$ denotes the set of all nonnegative real numbers. We assume that $\mathcal{D}$ is a nonempty subset of a Banach space $\mathcal{B}$ with norm $\Vert \cdot \Vert$, $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ a mapping and $F(\mathcal{G}) = \{t\in \mathcal{D}: \mathcal{G}t = t\}$.

A mapping $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is called non-expansive if $\Vert \mathcal{G}x-\mathcal{G}y \Vert \leq \Vert x-y \Vert$, for all $x, y\in \mathcal{D}$. A Banach space $\mathcal{B}$ is said to be uniformly convex if for any $\epsilon\in (0, 2]$ there exists a $\delta = \delta (\epsilon) > 0$ such that if $x, y \in \mathcal{B}$, $x\neq y$ with $\Vert x \Vert \leq 1$, $\Vert y \Vert \leq 1$ and $\Vert x-y \Vert \geq \epsilon$, then

However to find the fixed points of some operators is not an easy task, that's why we use the iterative schemes to approximate them. In 1979, Reich ^[1] proved weak convergence theorems for non-expansive mappings in Banach spaces and then several authors introduced the iterative schemes to approximate the fixed points of different nonlinear mappings, e.g. Mann scheme ^[2], Ishikawa scheme ^[3] and others ^[4,5]. Most of the problems in differential equations, delay differential equations, fractional differential equations, etc. have no exact solutions. So iterative schemes have to use to approximate the solutions of such problems.

The following iterative schemes have been introduced by Agrawal et al. (S) ^[6], Gursoy and Karakaya (Picard-S) ^[7], Thakur et al. (Thakur-New) ^[8], respectively. With initial point $\tau_0\in \mathcal{D}$, the sequence $\{\tau_{n}\}$ is developed as follows:

The following iterative scheme is introduced by Ali and Ali ^[9]. In this scheme the sequence $\{\tau_{n}\}$ with initial point $\tau_0\in \mathcal{D}$ is defined as follows:

where $\{\theta_n\}$ and $\{\mu_n\}$ are sequences in $(0, 1)$ called control sequences. Authors proved in ^[9] that this scheme converges faster than S, Picard-S, Vatan ^[10], Thakur-New, $M^{*}$ ^[11] and $M$ ^[12] schemes for Zamfirescu mappings ^[13].

The purpose of this paper is to prove convergence results for non-expansive mappings using the iterative scheme (1.4). Moreover we also numerically show that the iterative scheme (1.4) converges faster than S, Picard-S, Thakur-New iterative schemes for a particular non-expansive mapping. Finally, we approximate the solution of a second order boundary value problem.

2.   Preliminaries

This section contains some lemmas and definitions that will be used in the next results.

Definition 2.1. A Banach space $\mathcal{B}$ is said to satisfy Opial's property ^[14] if for each weakly convergent sequence $\{\tau_{n}\}$ to $x\in \mathcal{B}$, the following inequality

holds, for all $y\in \mathcal{B}$ with $y\neq x$.

Definition 2.2. ^[15] A self mapping $\mathcal{G}$ on a Banach space $\mathcal{B}$ is said to be demiclosed at $y$, if for any sequence $\{\tau_{n}\}$ which converges weakly to $x$, and if the sequence $\{\mathcal{G}(\tau_{n})\}$ converges strongly to $y$, then $\mathcal{G}(x) = y.$

Lemma 2.1. ^[16] Let $\mathcal{D}$ be a nonempty closed and convex subset of a uniformly convex Banach space $\mathcal{B}$ and $\mathcal{G}$ a non-expansive mapping on $\mathcal{D}$. Then, $I-\mathcal{G}$ is demiclosed at zero, that is $\mathcal{G}x = x$.

Lemma 2.2. ^[17] Let $\mathcal{B}$ be a uniformly convex Banach space and $0 < a\leq s_{n}\leq b < 1$, $\forall$$n\geq 0$. Let $\{\tau_{n}\}$ and $\{\sigma_{n}\}$ be two sequences in $\mathcal{B}$ such that $\lim\limits_{n\to\infty}\sup \Vert \tau_{n}\Vert \leq w$, $\lim\limits_{n\to\infty}\sup \Vert \sigma_{n}\Vert \leq w$ and $\lim\limits_{n\to\infty} \Vert s_{n}\tau_{n}+(1-s_{n})\sigma_{n}\Vert = w$ holds, for some $w\geq 0$. Then $\lim\limits_{n\to\infty}\Vert \tau_{n}-\sigma_{n}\Vert = 0$.

Definition 2.3. ^[18] A mapping $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is said to satisfy condition $(I)$, if there is a nondecreasing function $\psi: \mathbb{R_{+}} \to \mathbb{R_{+}}$ with $\psi(0) = 0$ and $\psi(z) > 0$, $\forall z > 0$ such that $d(x, \mathcal{G}x)\geq \psi(d(x, F(\mathcal{G})))$, $\forall x\in \mathcal{D}$, where $d(x, F(\mathcal{G})) = \inf\{\Vert x-t\Vert : t\in F(\mathcal{G})\}$, $i.e.$, the distance between the point and set.

3.   Convergence results

Throughout this section, we presume that $\mathcal{D}$ is a nonempty, closed and convex subset of a uniformly convex Banach space $\mathcal{B}$ and $\mathcal{G}:\mathcal{D}\to \mathcal{D}$ is a non-expansive mapping. Now, we prove the following useful lemmas which are used to prove the next results of this section.

Lemma 3.1. Let $\{\tau_{n}\}$ be a sequence developed by the iterative scheme $(1.4)$, then $\lim\limits_{n\to\infty}\Vert \tau_{n}-t\Vert$ exists for all $t\in F(\mathcal{G})$.

Proof. Let $t\in F(\mathcal{G})$ and $\{\tau_n\}\in \mathcal{D}$. From $F$ iteration (1.4), we get

From (3.1), we get

Also by (3.2), we get

Thus the sequence $\{\Vert \tau_n-t\Vert\}$ is decreasing and bounded below for all $t\in F(\mathcal{G })$. Hence, $\lim\limits_{n\to\infty}\Vert \tau_n-t\Vert$ exists.

Lemma 3.2. Let $\{\tau_{n}\}$ be a sequence developed by the iterative scheme (1.4) and $F(\mathcal{G})\neq \emptyset$. Then $\lim\limits_{n\to\infty}\Vert \tau_{n}-\mathcal{G}\tau_{n}\Vert = 0$.

Proof. In view of Lemma 3.1, $\lim\limits_{n\to\infty}\Vert \tau_n-t\Vert$ exists for $t \in F(\mathcal{G})$. Presume that,

From (3.1), (3.2) and (3.4), we have

Since $\mathcal{G}$ is non-expansive mapping, we have

Now,

So

Using (3.6) and (3.7), we get

And

So

From (3.5) and (3.9), we have

Thus,

Hence,

From (3.11) and Lemma 2.2, we have

Now, we prove the following weak convergence theorem for non-expansive mappings via the iterative scheme (1.4).

Theorem 3.1. Presume that $\mathcal{B}$ is equipped with Opial's property, then the sequence $\{\tau_{n}\}$ developed by the iterative scheme $F$ in $(1.4)$ converges weakly to a fixed point of the mapping $\mathcal{G}$.

Proof. From Lemma 3.1, we get $\lim\limits_{n\to\infty} \Vert \tau_n-t\Vert$ exists. Now our purpose is to show that $\{\tau_n\}$ does not have different weak sub-sequential limits in $F(\mathcal{G })$. Let $p$ and $q$ be two weak sub-sequential limits of $\{\tau_{n_{j}}\}$ and $\{\tau_{n_{k}}\}$, respectively. Where $\{\tau_{n_{j}}\}$ and $\{\tau_{n_{k}}\}$ are two subsequences of $\{\tau_n\}$. From Lemma 3.2, $\lim\limits_{n\to\infty}\Vert \tau_n-\mathcal{G }\tau_n\Vert = 0$ and by Lemma 2.1, $I-\mathcal{G}$ is demiclosed at zero. Thus $(I-\mathcal{G})p = 0$, that is, $p = \mathcal{G}p$. Similarly, $q = \mathcal{G}q$.

Now it is enough to show that $p = q$. If $p\neq q$, then applying Opial's property, we obtain

which is a contradiction. Hence $p = q$. It concludes that $\{\tau_{n}\}$ converges weakly to a fixed point of $\mathcal{G}$.

Theorem 3.2. The sequence $\{\tau_{n}\}$ developed by the iterative scheme $F$ in $(1.4)$ converges to a fixed point of $\mathcal{G}$ if and only if $\lim\limits_{n\to\infty}\inf d(\tau_{n}, F(\mathcal{G})) = 0$.

Proof. First part is trivial. Now we prove the converse part. Presume that $\lim\limits_{n\to\infty}\inf d(\tau_{n}, F(\mathcal{G})) = 0$. From Lemma 3.1, $\lim\limits_{n\to\infty} \Vert \tau_n-t\Vert$ exists, for all $t\in F(\mathcal{G})$ and by hypothesis $\lim\limits_{n\to\infty} d(\tau_n, F(\mathcal{G})) = 0$.

Now our assertion is that $\{\tau_n\}$ is a Cauchy sequence in $\mathcal{D}$. As $\lim\limits_{n\to\infty} d(\tau_n, F(\mathcal{G})) = 0$, for a given $\lambda > 0$, there exists $N\in \mathbb{N}$ such that for all $n\geq N,$

Specifically, $\inf\{\Vert \tau_{N}-t\Vert : t\in F(\mathcal{G})\} < \frac{\lambda}{2}$. So there exists $t\in F(\mathcal{G})$ such that

Now for $m, n\geq N$,

Thus, $\{\tau_{n}\}$ is a Cauchy sequence in $\mathcal{D}$, so there exists an element $\ell \in \mathcal{D}$ such that $\lim\limits_{n\to\infty} \tau_{n} = \ell$. Now $\lim\limits_{n\to\infty} d(\tau_{n}, F(\mathcal{G})) = 0$ implies $d(\ell, F(\mathcal{G})) = 0$, hence we get $\ell\in F(\mathcal{G})$.

By applying condition $(I)$, we now prove the following strong convergence result.

Theorem 3.3. Presume that the mapping $\mathcal{G}$ satisfies condition $(I)$. Then the sequence $\{\tau_{n}\}$ developed by the iterative scheme $F$ in $(1.4)$ converges strongly to a fixed point of $\mathcal{G}$.

Proof. We already proved in Lemma 3.2 that

Applying condition $(I)$ and Eq $(3.12)$, we obtain

And hence,

So by Theorem 3.2, the sequence $\{\tau_{n}\}$ converges strongly to a fixed point of $\mathcal{G}$.

Now, we present the following example to compare (numerically) the speed of convergence of iterative schemes (1.1)–(1.4) for a non-expansive mapping.

Example 3.1. Let $\mathcal{B} = \mathbb{R}^{3}$ be a Banach space with the usual norm, and $\mathcal{D} = \{x\in\mathbb{R}^{3}:||x||\leq1\}$ the unit ball in $\mathbb{R}^{3}$. Define $\mathcal{G}:\mathcal{D}\rightarrow \mathcal{D}$ by

It can be easily verify that $\mathcal{G}$ is non-expansive mapping but not contraction. Now we choose control sequences $\theta_n = 0.5$ and $\mu_n = 0.4$ with initial guess $x_1 = 0.5$, $x_2 = 0.25$ and $x_3 = 0.15$, then the iterative schemes (1.1)–(1.4) converges to $t = (0.3, 0.3, 0.3)$.

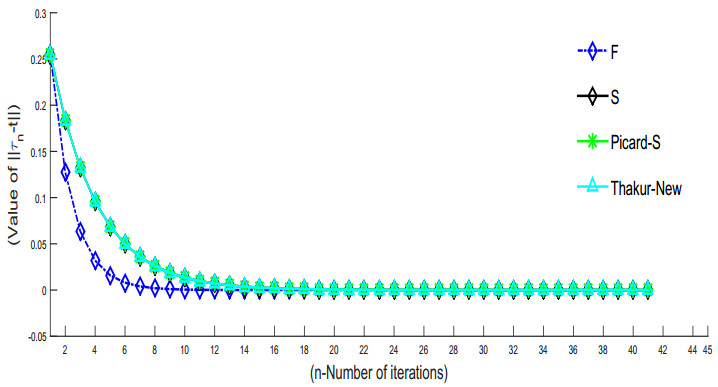
By Matlab R2015a, we exhibit that iterative scheme (1.4) converges faster than the iterative schemes (1.1)–(1.3), this is shown in Tables 1, 3 and Figure 1. It can be easily seen from Tables 1, 3 and Figure 1 that $F$ iterative scheme converges in twenty iterations while other iterative schemes converge in more than twenty iterations. We also showed error of the iterations at each step as shown in Tables 2 and 4. In each iteration, we can see that error is less than previous one. The error obtain by iterative scheme (1.4) is less than the error obtain by Thakur-New, S, Picard-S iterative schemes.

4.   Application to nonlinear ordinary differential equations

In this section, we approximate the solution of two-point boundary value problem of second order differential equation:

where $f:[0, 1]\times\mathbb{R}\rightarrow \mathbb{R}$ is a continuous function.

Let $\mathcal{B} = C[0, 1]$ be the space of all continuous function defined on $[0, 1]$ with maximum norm. Green's function associated to $(4.1)$ is defined by

Many authors studied the existence of the solution of problem $(4.1)$ (e.g. see ^[19,20,21]). Now we approximate the solution of problem $(4.1)$ by utilizing iterative scheme (1.4) with the following assumption:

$(C_1) \; \vert f(t, a)-f(t, b) \vert \leq \max_{a, b \in [0, 1]} \vert a-b \vert$, for all $t\in [0, 1]$.

Theorem 4.1. Let $\mathcal{B} = C[0, 1]$ be a Banach space with maximum norm. Let $\{\tau_n\}$ be a sequence defined by $F$ iterative scheme $(1.4)$ for the operator $\mathcal{G}:\mathcal{B}\rightarrow \mathcal{B}$ defined by

Assume that the condition $(C_1)$ is satisfied. Then the sequence defined by $F$ iterative scheme $(1.4)$ converges to a solution, say $x\in \mathcal{B}$ of the problem $(4.1)$.

Proof. Observe that $x\in \mathcal{B}$ is a solution of (4.1) if and only if $x\in \mathcal{B}$ is a solution of the integral equation

Let $x, y \in \mathcal{B}$ and using $(C_1)$, we get

As $\int_{0}^{1} G(t, s)ds = -\frac{t^{2}}{2}+\frac{t}{2}$, for all $t\in [0, 1]$, $\sup_{t\in [0, 1]}\int_{0}^{1}G(t, s)ds = \frac{1}{8}$, we obtain

Thus $\mathcal{G}$ is non-expansive mapping. Hence $F$ iterative scheme converges to the solution of (4.1).

Example 4.1. Consider the following differential equation

The exact solution of problem (4.3) is given by

The operator $\mathcal{G}:C[0, 1]\to C[0, 1]$ is defined by

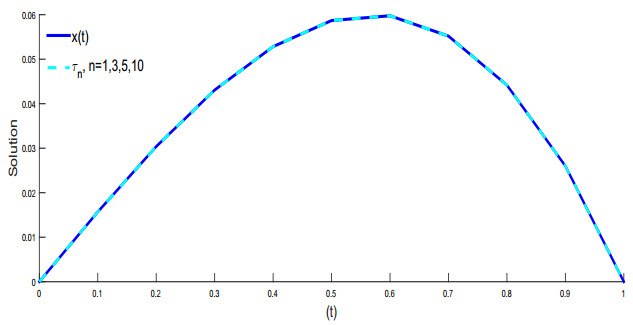
for initial guess $\tau_{0}(t) = t(1-t), \; t\in [0, 1]$ and control sequence $\theta_{n} = 0.85, \; n\in \mathbb{Z_+}$, we observe that $F$ iterative scheme converges to the exact solution of problem (4.3) for the operator defined in Eq (4.4) which is shown in Table 5 and Figure 2. Further, it can be easily seen in Table 5, the absolute error at each step of $F$ iterative scheme is zero.

5.   Conclusions

In this paper, the convergence analysis of the iterative scheme $F$ has been studied for non-expansive mappings. Further, $F$ iterative scheme has been successfully applied to the solution of a boundary value problem of second order ordinary differential equation. We compared the rate of convergence of iterative schemes (1.1)–(1.4) numerically for non-expansive mapping. High rates of convergence have been achieved. The numerical results show that the presented process (1.4) outperforms other iterative schemes.

Acknowledgments

The first author would like to thank to the University Grant Commission, India for providing the Senior Research Fellowship. The authors are grateful to the anonymous referees for their valuable suggestions and fruitful comments.

Conflict of interest

The authors declare no conflict of interest.