Fever is a common symptom of many diseases. Fever temporal patterns can be different depending on the specific pathology. Differentiation of diseases based on multiple mathematical features and visual observations has been recently studied in the scientific literature. However, the classification of diseases using a single mathematical feature has not been tried yet. The aim of the present study is to assess the feasibility of classifying diseases based on fever patterns using a single mathematical feature, specifically an entropy measure, Sample Entropy. This was an observational study. Analysis was carried out using 103 patients, 24 hour continuous tympanic temperature data. Sample Entropy feature was extracted from temperature data of patients. Grouping of diseases (infectious, tuberculosis, non-tuberculosis, and dengue fever) was made based on physicians diagnosis and laboratory findings. The quantitative results confirm the feasibility of the approach proposed, with an overall classification accuracy close to 70%, and the capability of finding significant differences for all the classes studied.
%An abstract is a brief of the paper; the abstract should not contain references, the text of the abstract section should be in 12 point normal Times New Roman.
1.
Introduction
Fever is a frequent symptom that can be the manifestation of many pathologies [1]. It can be found at different clinical settings: primary, emergency, hospital, or ambulatory care. Besides, temperature temporal profile exhibits a significant variability depending on subject, age, sex, anatomy, pathology, and time of day, among many other possible factors [2,3]. As a consequence, the diagnosis of fever's causes can be challenging and it can also be a costly task in terms of time and clinical resources: blood cultures, haemoglobin, creatinine, etc. [4]. This is specially critical in resource-limited countries [5], such as many Asian, South-American, and African countries, where fever-related diseases are most prevalent, and the few resources available are geographically very scattered.
The recent advent of affordable long-term ambulatory body temperature monitors and other similar wearable devices, has provided a new perspective on the analysis of temperature data [6]. The continuous readings now available enable a richer physiological analysis beyond the plain dichotomy fever/no fever [7]. If this analysis could contribute to the diagnosis of fever's causes, it would become a very cost-effective tool in contrast to current methods. The main hypothesis is that different pathologies exhibit different fever dynamics or patterns [1] that could be detected by a suitable algorithm.
Body temperature time series analysis is a field only recently explored using non-linear methods. In contrast to other physiological data such as RR-interval or electroencephalogram (EEG) time series, temperature has not been so widely analysed yet. However, there are some promising results that illustrate the potential of these data, mainly as an unobtrusive and inexpensive diagnosis aid. For example, in [8], the authors propose a logistic model to classify temperature records from patients that did or did not develop a fever episode, combining Permutation Entropy (PE) and Approximate Entropy (ApEn). The non-linear processing of suitable temperature data can even become an early marker of fever episodes before they are actually developed, in order to anticipate diagnosis and treatment, as demonstrated in [9]. Temperature and sepsis have also been studied in a number of papers. In [10], researchers used temperature patterns to anticipate hospital-acquired infections in an intensive care unit. Papaioannou et al. [11], developed a diagnosis technique based on the Wavelet transform and Multiscale Entropy (MSE) of temperature data to distinguish among subjects with inflammatory response syndrome, sepsis, and septic shock. Other studies have been focused on the role of temperature as a marker of patient prognosis, such as [12,13]. A general view of possible applications of body temperature data analysis was provided in [7].
An even more recent body of research about temperature is devoted to finding differences not only between healthy and ill subjects, or between fever and no-fever, but to finding differences among a group of diseases that manifest by means of changes in the temperature level or/and dynamics. Along this line, the work described in [14] trains an artificial neural network using several features to classify infectious and non-infectious diseases from 24-hour continuous tympanic temperature recordings. Using a similar dataset, the study in [15] successfully classified time series from tuberculosis, dengue, infectious, and non-infectious disease types. They used a multi-feature approach, including the Fast Fourier Transform, entropy, energy, power, many other coefficients, and visual observations.
The present study addresses the same problem of trying to classify diseases where fever is one of the main symptoms. In contrast to previously commented works such as [14] and [15], the classification will be based on a single non-linear feature, Sample Entropy (SampEn). Although arguably a single feature could provide a lower classification performance than a more complete set, implementation on a real computer-aided diagnosis tool will be simpler and faster. We also hypothesized that SampEn is able to capture much of the information that is included in other features such as temperature frequency content, or variations [16], and therefore the detrimental effect on performance will be minimised. SampEn will also be reinforced with a suitable non-uniform downsampling method.
2.
Materials and methods
2.1. Sample Entropy
The SampEn method was proposed in [17]. This method belongs to a family of very similar methods that includes ApEn [18] and FuzzyEn [19], among many other variations and customizations [20,21]. SampEn was introduced as an improvement over ApEn, since SampEn does not count self-matches, the results are more consistent, and the algorithm is more efficient. FuzzyEn is based on SampEn, but replacing the crisp dissimilarity measure by a suitable continuous function.
Although improvements have been sequentially introduced from ApEn up to FuzzyEn, each method has its optimal field of application where it outperforms the other statistics, and not necessarily in that order. In principle, FuzzyEn is expected to yield the best performance [22,23], and, although SampEn could be considered a particular implementation of FuzzyEn, it outperforms FuzzyEn in applications such as in [24]. In a few cases, ApEn was the best one [8,13]. A preliminary exploratory analysis was conducted in the present study in order to find out which one was the optimal statistic, SampEn, as will be justified in Section 3.
The temperature data is featured by a time series x of length N: x={x0,x1,x2,⋯,xN−1}. Given a subsequence length m, with m<<N, and starting at the i−th sample, xi={xi,xi+1,xi+2,…,xi+m−1}, xi is compared with all the other possible subsequences in the time series xj,j≠i. This comparison is quantified in terms of a maximum distance between pairs of samples, given by dij=max(|xi+k−xj+k|),0≤k≤m−1. Another input parameter, r, is used as a distance threshold to consider two subsequences similar.
For example, let xi be {−0.8762,1.3210,0.2009} and xj be {1.2392,1.0931,0.7841}, with r=0.25, and m=3. The distance between pairs of samples is in this case dij=max(|−0.8762−1.2392,1.3210−1.0931,0.2009−0.7841|)=max(|−2.1154,0.2279,−0.5832|)=2.1154. Since dij>r, these two subsequences are not considered similar.
The number of similar subsequences to xi found in x is stored in a counter Bmi(r). This process is repeated for each possible xi, and the final average number of matches is computed as:
As in the previous example, let xi={−0.8762,1.2128,0.1717} and xj={−1.0191,1.3433,0.3913}, again with r=0.25 and m=3. The distance between pairs of samples is in this case dij=max(|−0.8762+1.0191,1.2128−1.3433,0.1717−0.3913|)=max(|0.1429,−0.1305,−0.2196|)=0.2196. Since now dij≤r, these two subsequences are considered similar, and therefore the counter is increased by 1, Bmi(r)←Bmi(r)+1.
The length of the subsequences, m, is then increased by 1, and the previous process of computing the distances and counter averages is repeated, obtaining a new counter termed Am(r) (This new counter, in fact, could be considered as Am(r)=Bm+1(r)). From the two counters for two consecutive lengths, SampEn can finally be obtained as:
An implementation example is shown in Algorithm 1. The specific value of parameter N in the SampEn algorithm was set in advance by the clinical procedure for body temperature recording, as described in Section 2.3. The value of the other two parameters, although usually recommended to lie in the vicinity of m=2 and r=0.25, was optimised using a grid search [25]. The parameter space explored corresponded to the region defined by 1≤m≤6 and 0.1≤r≤0.5.
2.2. Trace segmentation
An additional approach we used to reinforce the role of the possible temperature peak distribution was to apply a non-uniform downsampling scheme (the effects of uniform downsampling on SampEn have been studied elsewhere, such as in [26,27,28]). Specifically, we applied the so-called Trace Segmentation (TS) method [29,30,31]. The adequacy of this method to the purpose of this experiment stems from the fact that TS samples the input signal at those points where the greatest signal variation takes place.
Mathematically, the TS method proceeds as follows. Given an input time series, x={x0,x1,x2,⋯,xN−1}, and accumulated derivative is obtained as:
where k∈[1,N−1], and TS0=0. The last point, TSN−1, provides the maximum value of the accumulated derivative, from which the amplitude of the sampling intervals Δ can be obtained as Δ=TSN−1N′−1, being N′ the desired number of output samples, with N′<N. The minimum index i of x for which TSi exceeds an integer multiple q of Δ provides a sampling point for the new output sequence x′, analytically:
with x′0=x0. TS reinforces the presence of peaks in a non-linear way. Its algorithm is shown in Algorithm 2.
2.3. Experimental dataset
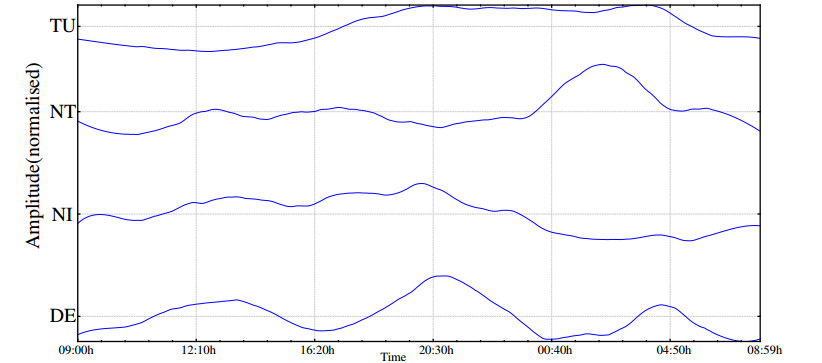
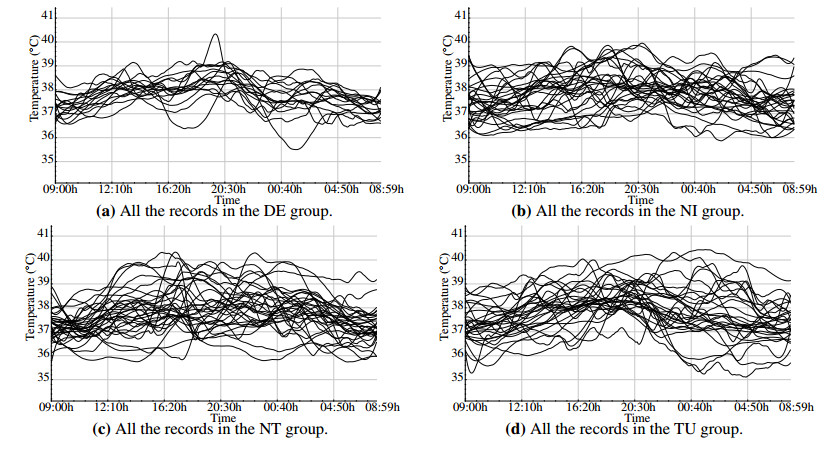
A total of 103 body temperature time series were included in the experimental dataset (Figure 1). The duration of each record was 24h, sampled at 1 sample/minute, 1440 samples. The acquisition started at 9:00 AM, and ended at 8:59 AM of the following day. The records were preprocessed for artifact minimisation. The final diagnosis of each patient was established according to other clinical findings. This experimental dataset was composed of the following groups:
● DE: Dengue. This group contains 16 records of dengue patients. All the records in this group are shown in Figure 1a.
● NI: Non-Infectious. This group contains 28 records from patients with no evidence of infection. All the records in this group are shown in Figure 1b.
● NT: Non-Tubercular. This group contains 31 records of bacterial infections that do not cause tuberculosis. All the records in this group are shown in Figure 1c.
● TU: Tuberculosis. This group contains 28 records of tuberculosis patients. All the records in this group are shown in Figure 1d.
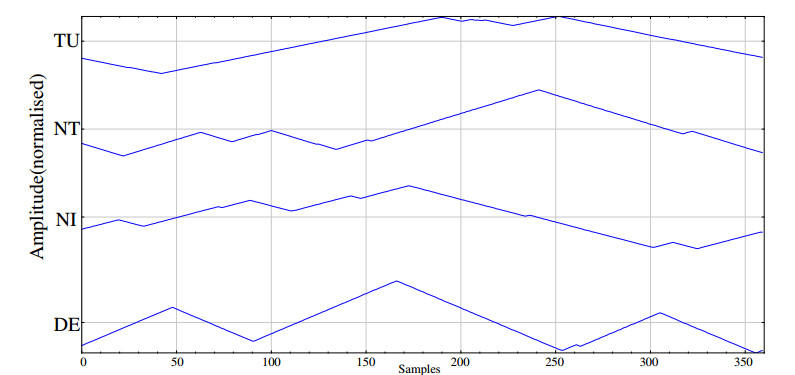
This experimental dataset is a superset of that used in [15], where further information of the clinical setting and acquisition stage can be found. A more detailed example plot of the database is depicted in Figure 2.
3.
Experiments and results
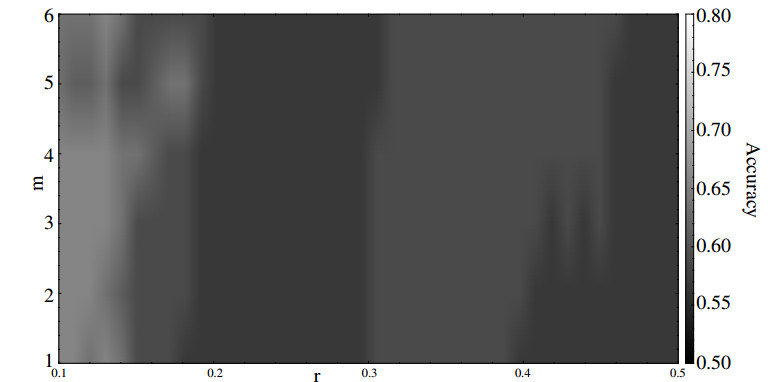
Using only SampEn as the distinguishing feature, all the classes in the experimental dataset were compared in pairs. For each one of these pairs, a grid search was conducted in order to find the best combination of m and r parameters for a maximum classification performance. In general, there was not a great variation in this performance. To illustrate this point, Figure 3 shows the heatmap of the classification achieved for pair DE-NI. The maximum accuracy was around 0.60, for low r values.
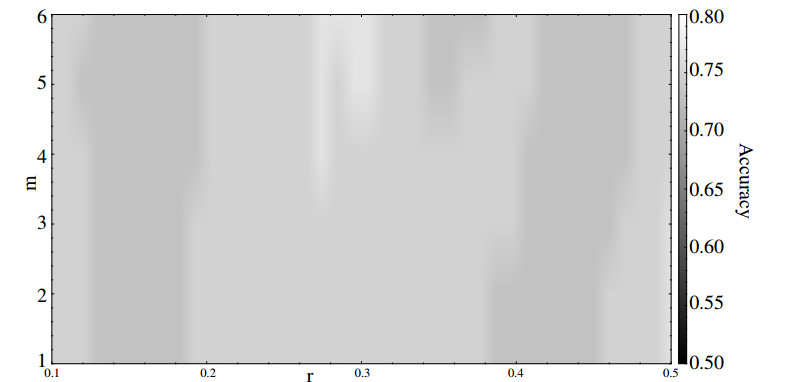
In the same way, Figure 4 depicts the heatmap for the accuracy achieved using classes NI and TU. In this case, the maximum performance was 0.77 for the parameter space defined by m>3 and 0.26<r<0.31, although there is a small region with the same performance at r=0.5 and m<4, at the lower right corner of the plot. Anyway, the accuracy in this case was above 0.70 in practically the entire region explored.
The analysis of each pair yielded a different optimal parameter configuration, as can be inferred from Figures 3 and 4. Therefore, the resulting optimal setting in each case was used for the classification analysis, using Sensitivity, Specificity, and Accuracy. The statistical significance of the results was assessed using an unpaired Wilcoxon-Mann-Whitney test, with the α threshold set at 0.05. The results of this analysis using SampEn are shown in Table 1, including the p−value, and the m and r values for which such performance was achieved. It is important to note that other cases not reported in Table 1 also achieved a very similar accuracy, if not the same. There were also configurations with higher accuracy, but at the expense of very unbalanced Sensitivity and Specificity, or without statistical significance, that are not included in Table 1.
The experiments were repeated using also ApEn and FuzzyEn, but the best performance was achieved using SampEn. For example, while SampEn accuracy was 0.77 for NI-TU, ApEn was 0.75, with p = 0.0014. The other ApEn results were similar, but always slightly below those of SampEn. Even for NI-NT, ApEn did not achieve statistical significance. FuzzyEn performance was also lower than that of SampEn, only for NT-NU was it higher, but just 0.65 against 0.64, with p = 0.0335. In addition, FuzzyEn needs the customisation of another parameter.
In a more realistic scenario, each class would have to be segmented from a set including all the pathologies simultaneously. In this regard, experiments were repeated where the pairs to be segmented were a single class on one side, and all the other classes together on another side. The results in this case are shown in Table 2. Only TU and NI classes could be significantly segmented from the other sets, with an accuracy equal or slightly greater than 70%.
Since fever profiles usually exhibit a strong temporal component correlated with the underlying diagnosis, like slow temperature variations [32], early fever onset, persistent hyperthermia, or a spiking pattern [33], an additional time series analysis was carried out using only part of the data. Specifically, the 20 first hours, the 20 central hours, and the last 20 hours of the records (1200 samples). The purpose of this segmentation was to study the possible temporal distribution of the differences between the fever dynamics.
Using the first 20 hours of the records, the overall classification performance decreased in terms of number of separable pairs. Classes NT-TU become undistinguishable, whereas using the complete 24h records the accuracy in this case was 0.64 with p = 0.0467. In the same way, using the last 20 hours, only DE-TU and NI-TU were significantly separable. On the contrary, using the central 20 hours, the performance was very similar to that shown in Table 1 with a swapped separable pair: DE-NT classes could be classified with an accuracy of 0.71, with p = 0.0433, but not NT-TU any more.
Finally, TS was applied as a new preprocessing stage in order to find out if classification results could be improved by emphasising the temporal differences between classes. The percentage of samples remaining after downsampling were: 95%, 50%, and 25%. The numerical results achieved are shown in Table 3. This was the only scheme (TS+SampEn) able to find statistically significant differences between all the pairs studied, although with low accuracy in some cases. Visually, the TS effect is shown in Figure 5.
4.
Discussion
The classification of pathologies based on a single feature of their fever profile is a very difficult task, but with a potentially huge impact on the healthcare system of many countries. This study analysed 4 different common pathologies in order to find out whether such classification was possible or not.
Using the complete records, the two classes most easily distinguished using only SampEn were NI and TU, as shown in Table 1. Other significant classification results were achieved for classes DE and TU, and classes NI and NT, with an overall accuracy of at least 70%. The poorest performance, but still statistically significant, was achieved for classes NT and TU, with an accuracy of 64%. It was not possible to distinguish between DE and NI, and DE and NT, in any case included in the analysis related to results in Table 1. Related entropy measures as ApEn and FuzzyEn did not improve the results achieved using SampEn.
With regard to the optimal parameter values, m=3 seemed to yield good results across all the significant cases studied. There was a slightly greater variability in terms of r parameter. For DE-TU and NI-NT, r=0.10 was the best choice. Although not reported in Table 1, this configuration for r also yielded an accuracy above 70% in the NI-TU case. The classification of NT-TU was more demanding and critical, and only values of r in the 0.41-0.45 region yielded statistically significant results.
Windowing was another technique tried in the experiments in order to find out if the distinguishing information was not uniformly distributed along the entire records. With a window length of 20h, the accuracy achieved was lower than using the entire records. In principle, we can rule out possible border effects in the experimental dataset.
The duration of the time series can also play a key role in the classification performance potential. Although the current available length, 1440 samples, suffices according to the general recommendations in this SampEn context [17], or it is even longer than in other applications [21], it could become insufficient for greater m values, or from a physiological standpoint, since some pathologies exhibit a longer pattern, for example 48h in Malaria [1]. In addition, provided there are not non-stationarities in the time series, the longer, usually the better [34]. In the specific case of fever, given its marked cyclic behaviour in most cases [35], noise or artifact robustness could be arguably increased just by having more repeated temporal patterns or data redundancy.
The segmentation of a single disease from the complete set is even more difficult. Significant differences were found only in two cases, for TU and NI (Table 2). However, even in this unfavourable scenario, being able of diagnosing TU or NI with a 70% accuracy is a good starting point for further studies, and such a tool can be complementary to current systems in place by itself.
The method that seemed to perform best was to add TS before computing SampEn to reinforce the differences between classes. It was the only case, using a 25% percentage, to find differences between all the pairs as shown in Table 3, and it is the most promising future line of research. The goal should be to increase the accuracy up to as close to 80% as possible.
5.
Conclusion
Fever can be the manifestation of a great number of pathologies, and its identification is not straightforward, specially in scarcely equipped clinical facilities.
A few studies have been published recently trying to find a correlation between several fever data features and the underlying pathology with promising results [15]. Our goal was to further simplify this approach using a single non-linear feature, SampEn.
The results obtained were very similar to those obtained using many more features. Applying TS, significant differences were found for all cases. However, further studies are necessary before such a tool can be implemented in real clinical settings, including more and longer records, from different hospitals, and with a healthy reference group. Anyway, at least a similar tool could be arguably used as an additional diagnosis aid, in combination with other tools currently in place. No specific classifier was proposed since this was a feasibility study aimed at exploring the potential of the scheme proposed.
There is an important feature of body temperature regulation that has not been exploited in the dataset used in this work and could have important clinical implications from a diagnosis point of view. Not only can temporal temperature variations be representative of the underlying pathology, but also their local variations. The concept of a single body temperature is not correct, since at least there are three different settings referred to as body temperature in clinical procedures: core, peripheral, and basal body temperature [6], which can also be measured at many body locations. Relative changes between core and peripheral temperature have already been demonstrated to be clinically significant [9], representative of the temperature regulatory system output, and future studies should include more than a single location simultaneously in order to find out if differences among febrile diseases become more apparent.
The study concludes that a single mathematical feature such as SampEn, could be able to classify the pathologies included in the experimental dataset significantly. With further studies as stated above, exploring more entropy related measures, and more optimal preprocessing techniques such as TS, it can be hypothesized that the classification accuracy could be far greater than the 70% currently achieved. It can also be hypothesized that the difficulty of finding differences between some classes can be due to the coexistence of more than a single factor that causes the fever, among other possible interfering factors, and the temperature records should be more deeply characterised before trying to classify them.
Acknowledgements
The Spanish researchers were supported by the Torres Quevedo program of the Spanish Ministry of Science, code PTQ-16-08538. The Indian researchers were supported by the Kasturba Medical College and Hospitals, Manipal University, Mangaluru, Karnataka, India.
Conflict of interest
The authors declare that they have no conflict of interest.










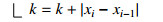
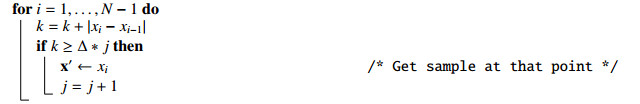
 DownLoad:
DownLoad: