Impulsive control for stationary oscillation of nonlinear delay systems and applications

1.   Introduction

In many real systems there are two common phenomena: Delay effects and impulsive effects ^{[1,2,3,4,5,6,7,8]}. For example, time delays will inevitably occur in the communication and response of neurons owing to the unavoidable finite switching speed of amplifiers in the electronic implementation of analog neural networks ^[3,4]. In many nonnegative and compartmental models, the transfers of material, energy or information between compartments are not instantaneous and some information of the past system states are always considered for capturing the realistic dynamics of systems, which leads to time delay systems ^[5,6]. Moreover, it has been shown that the existence of time delays may lead to oscillation, instability and other bad performances of systems ^[7,8].

Examples of impulsive phenomena can be found in many fields such as biological neural networks, bursting rhythm models in pathology, information science, frequency-modulated signal processing systems and telecommunication ^{[1,2,9,10,11,12]}. Such kinds of systems are characterized by abrupt changes of state at certain instants, in the form of impulses, which cannot be well described by using pure continuous or pure discrete models. Additionally, impulse as a control method has been applied to many interesting fields such as ecosystems management, orbital transfer of satellites, optimal control of economic systems, synchronization of chaos-based secure communication systems and so on ^{[13,14,15,16]}. The main idea of impulsive control is to change the states of continuous dynamic systems via discontinuous control inputs at certain time moments. There are many cases where impulsive control can make better performance than continuous control ^[17,18,19]. Therefore, it is of great theoretical and practical significance to study and develop the fundamental theory of impulsive nonlinear delay systems. Up until now, numerous works dealing with the fundamental theory such as existence-uniqueness, differentiability, controllability, boundedness, oscillation, stability and periodic solution problems for impulsive functional differential equations have been reported in the literature, see ^{[20,21,22,23,24,25,26,27,28]} and the references therein. In particular, Alzabut and Abdeljawad ^[25] investigated the existence of a globally attractive periodic solution for a class of impulsive delay logarithmic population model. Recently, Alzabut et al. ^[26] further investigated the almost periodic solutions of the impulsive delay logarithmic population model by employing the contraction mapping principle and Gronwall-Bellman inequality. Considering the fact that the existing work mainly focuses on some special scalar delay differential equations with impulses, Yang and Xu ^[27] and Weng and Sun ^[28] studied the stationary oscillation for generalized nonlinear impulsive delay differential equations by establishing an exponential estimate for delay differential inequality with impulsive initial condition and employing Banach fixed point theorem. The obtained results extended and improved some earlier works. However, one may note that all of those results ^{[25,26,27,28]} dealing with periodic solution problems of impulsive delay differential equations have a common property that the system still admits a stationary oscillation even there is no impulsive effects. Since impulses can make an unstable system stable, it is nature to ask, under impulsive control, whether there exists some criteria that can ensure the delay systems admits a stationary oscillation even it is originally unstable or divergent. More specifically, when $a_1(t) < a_2(t)$ in ^[26], $\alpha(t) < \beta(t)$ in ^[26] and some of the eigenvalues of the parameter matrix $A(t)$ have positive real parts in ^[27,28], it is a question whether we can design some impulsive control strategies to ensure the existence of stationary oscillation for those systems. This is a real problem in applications.

Motivated by the above statements, in this paper, we shall further consider the impulsive nonlinear delay systems which is same as that in ^[27,28]. The difference is that, from the impulsive control point of view, some new sufficient conditions ensuring the existence of stationary oscillation are derived by using the inequality technique that has been given by ^[29]. Based on the obtained results, we further consider the single species logarithmic population model and establish a new criterion to guarantee the existence of positive stationary oscillation. The organization of this paper is as follows. In Section 2, we introduce some notations and definitions. In Section 3, we present the main results on stationary oscillation of the addressed equations. In Section 4, three numerical examples and their computer simulations are given to show the effectiveness of our development control method. Finally, we shall make concluding remarks in Section 5.

2.   Preliminaries

Notations. Let $\mathbb{R}$ denote the set of real numbers, $\mathbb{R}_{+}$ the set of positive real numbers, $\mathbb{Z}_+$ the set of positive integers, $\mathbb{R}^{n\times m}$ the $n\times m$-dimensional real spaces and $\mathbb{R}^{n}$ the $n$-dimensional real spaces equipped with the norm $\|x\| = \sum_{i = 1}^n|x_i|$. The impulse times $t_{k}$ satisfies $0\leq t_{0} < t_{1} < \ldots < t_{k}\rightarrow \infty$ as $k\rightarrow \infty$. For any interval $J\subseteq \mathbb{R}$, set $S\subseteq \mathbb{R}^k (1\leq k\leq n), C(J, S) = \{\varphi:J\rightarrow \ S$ is continuous$\}$ and $PC(J, S) = \{\varphi:J\rightarrow \ S$ is continuous everywhere except at finite number of points $t$, at which $\varphi(t^{+})$, $\varphi(t^{-})$ exist and $\varphi(t^{+}) = \varphi(t)\}.$ In particular, for a given $\tau\in [0, \infty),$ let $\mathbb{PC} = PC([-\tau, 0], \mathbb{R}^{n})$ with the norm $\|\bullet\|_\tau$ defined by $\|\varphi \|_\tau = \sup_{-\tau\leq s\leq 0}\|\varphi(s)\|.$ $\alpha\vee\beta$ denotes the maximum value of $\alpha$ and $\beta.$ $[\bullet]^\ast$ denotes the integer function.

Consider the following nonlinear delay systems with impulses:

where $\phi\in \mathbb{PC},$ $A(t) = (a_{ij}(t))_{n\times n}\in PC(\mathbb{R}_+, \mathbb{R}^{n\times n})$ and $f(t, x_t): \mathbb{R}_+\times \mathbb{PC}\rightarrow \mathbb{R}^{n};$ For each $t\geq t_0, \ x_t\in \mathbb{PC}$ is defined by $x_t(s) = x(t+s), s\in [-\tau, 0];$ For each $k\in \mathbb{Z}_+, \ I_k(t, x)\in C(\mathbb{R}_{+}\times \mathbb{R}^{n}, \mathbb{R}^{n}).$

In this paper, we make the following assumptions:

$(H_1)$ There exists a constant $\omega > 0$ such that $A(t+\omega) = A(t), \ f(t+\omega, \bullet) = f(t, \bullet), \ I_k(t+\omega, \bullet) = I_k(t, \bullet), \ t\in \mathbb{R}_+, \ k\in \mathbb{Z}_+;$

$(H_2)$ For given $\omega > 0$, there exists a constant $q\in \mathbb{Z}_+$ such that $t_{k+q} = t_k+\omega, \ I_{k+q}(t, \bullet) = I_{k}(t, \bullet), \ t\in \mathbb{R}_+, \ k\in \mathbb{Z}_+;$

$(H_3)$ There exists some positive functions $L_{ij}(t)\in PC(\mathbb{R}_+, \mathbb{R}_{+}^{n\times n})$ such that

where $i\in \Lambda$, $\varphi_1, \varphi_2\in \mathbb{PC}$, $t\in\mathbb{R}_+$, $\Lambda = \{1, 2, \cdots, n\}, \varphi_i = (\varphi_{i1}, \cdots, \varphi_{in})^T, i = 1, 2;$

$(H_4)$ There exists some positive constants $\rho_{ik}\in(0, 1)$ such that

where $u, v\in \mathbb{R}$, $t\in \mathbb{R}_+$, $i\in \Lambda$, $k\in \mathbb{Z}_+$;

$(H_5)\ a^\star_{ii} = \sup_{t\in [0, \omega]} a_{ii}(t), \ a^\star_{ij} = \sup_{t\in [0, \omega]} |a_{ij}(t)| (i\neq j), \ L^\star_{ij} = \sup_{t\in [0, \omega]} L_{ij}(t), i, j\in\Lambda.$

Remark 2.1. Under the above assumptions $(H_3)$ and $(H_4),$ the solution of Eq (1) exists on $[t_0, +\infty)$ and is unique ^[20]. In the following, denote by $x(t) = x(t, t_0, \phi)$ the solution of Eq (1) with initial value $(t_0, \phi)$. On the other hand, it should be noted that assumptions $(H_1)$ and $(H_3)$ imply that $a^\star_{ij}$ and $L^\star_{ij}$ exist in assumption $(H_5).$

Definition 2.1. A map $x: \mathbb{R}_+\rightarrow \mathbb{R}^n$ is said to be a $\omega$-periodic solution of Eq (1), if

(1) $x(t)$ is a piecewise continuous map with first-class discontinuity points and satisfies Eq (1);

(2) $x(t)$ satisfies $x(t+\omega) = x(t), t\neq t_k$ and $x(t_k+\omega^{+}) = x(t_k^{+}), k\in \mathbb{Z}_+.$

Definition 2.2. Let $x^\ast = x^\ast(t, t_0, \phi^\ast)$ be a solution of Eq (1) with initial value $(t_0, \phi^\ast).$ Then the solution $x^\ast$ is said to be a stationary oscillation of Eq (1), if

(1) $x^\ast$ is the unique $\omega$-periodic solution of Eq (1);

(2) For any other solution $x = x(t, t_0, \phi)$ of Eq (1) through $(t_0, \phi)$, it holds that

Lemma 2.1. (^[29]). Let $p\in \mathbb{R}, q\geq 0, \delta > 1$ be some real constants and function $f\in PC(\mathbb{R}, \mathbb{R}_+)$ satisfying

Assume that $p+q \delta-\frac{\ln \delta}{\sigma} < 0,$ where $\sigma\doteq\sup_{k\in \mathbb{Z}_+}\{t_k-t_{k-1}\},$ then Eq (2) has the following estimate:

in which $\lambda > 0$ is a constant.

Remark 2.2. In particular, when $p+q < 0,$ constant $\delta$ in Lemma 2.1 can be sufficiently close to $1^+.$ In this case, it is known that Eq (2) still has above estimate even there is no impulsive effects (see ^[30]). Since the aim of this paper is to consider the effect of impulsive control, in the following we will employ Lemma 2.1 under the assumption that $p+q > 0.$

Lemma 2.2. (^[27]).Assume that $(H_1)$ and $(H_2)$ hold. Then $Eq (1)$ has an $\omega$-periodic solution if there exists a $\phi\in \mathbb{PC}$ such that $x_{t_0+\omega}(t_0, \phi) = \phi,$ where $x(t, t_0, \phi)$ is a solution of $Eq (1)$ through $(t_0, \phi).$

3.   Main results

In this section, we shall present some results on stationary oscillation for Eq (1) via impulsive control.

Theorem 3.1. Assume that assumptions $(H_1)-(H_5)$ hold. Then Eq (1) admits a stationary oscillation, if there exists a constant $\sigma > 0$ such that $t_k-t_{k-1}\leq \sigma, \ k\in \mathbb{Z}_+, \sup_{i\in\Lambda, k\in \mathbb{Z}_+}\rho_{ik} < 1$ and

Proof. Let $x = x(t, t_0, \phi)$ and $y = y(t, t_0, \varphi)$ be two arbitrary solutions of Eq (1) with initial values $(t_0, \phi)$ and $(t_0, \varphi),$ respectively, where $x = (x_1, \cdots, x_n)^T\in \mathbb{R}^n, y = (y_1, \cdots, y_n)^T\in \mathbb{R}^n$ and $\phi, \varphi\in \mathbb{PC}.$ Consider an auxiliary function

Clearly, $\Gamma\in PC(\mathbb{R}, \mathbb{R}_+).$ Calculating the upper right derivative of function $\Gamma,$ it can be deduced from assumption $(H_3)$ that

where $\bar{\Gamma}(t) = \sup_{t-\tau\leq s\leq t}\Gamma(s).$

On the other hand, it follows from assumption $(H_4)$ that

Considering assumption (3) and using Lemma 2.1, we know that there exists a constant $\lambda > 0$ such that

i.e.,

Thus one may choose a $T\geq t_0$ such that

Define an operator

$\mathcal{F}: \hat{\phi}\rightarrow x_{t_0+\omega}(t_0, \hat{\phi}),$ where $\hat{\phi}\in \mathbb{PC}.$ Note that $x_{t_0+\omega}(t_0, \hat{\phi})\in \mathbb{PC},$ which implies that operator $\mathcal{F}$ maps the set $\mathbb{PC}$ into itself. By simple induction, it can be deduced that

Let $k$ be large enough such that $t_0+k\omega-\tau\geq T,$ then it holds from (4) that

Hence, we get that $\mathcal{F}$ is a contraction mapping in Banach space $\mathbb{PC}.$ Using Banach fixed point theorem, there exists a unique $\phi^\star\in\mathbb{PC}$ such that $\mathcal{F}\phi^\star = \phi^\star,$ which implies that there exists a unique $\phi^\star\in\mathbb{PC}$ such that $x(t_0+\omega, t_0, \phi^\star) = \phi^\star.$ By Lemma 2.2, it can be deduced that Eq (1) has exactly one $\omega$-periodic solution which is globally exponentially stable, i.e., Eq (1) admits a stationary oscillation and the proof is therefore complete. □

In particular, if $A(t)$ is a diagonal matrix, then the following simple result can be derived by Theorem 3.1.

Corollary 3.1. Assume that assumptions $(H_1)-(H_5)$ hold. Then Eq (1) admits a stationary oscillation, if there exists a constant $\sigma > 0$ such that $t_k-t_{k-1}\leq \sigma, \ k\in \mathbb{Z}_+, \sup_{i\in\Lambda, k\in \mathbb{Z}_+}\rho_{ik} < 1$ and

Remark 3.1. From the estimate of $D^+\Gamma$ in Theorem 3.1, one may observe that Eq (1) may not has stationary oscillation even it is divergent and if there is no impulsive effects. However, the criteria established in Theorem 3.1 and Corollary 3.1 tell us that the proper impulsive control strategies may contribute to system periodicity and guarantee the existence of stationary oscillation. This assertion will be further illustrated in Section 4.

Now, we consider the following special equations:

where $A(t) = (a_{ij}(t))_{n\times n},$ $B(t) = (b_{ij}(t))_{n\times n}\in PC(\mathbb{R}_+, \mathbb{R}^{n\times n})$ and $\tau(t): \mathbb{R}_+\rightarrow \mathbb{R}_+$ is the time-varying delay function. $D_k =$diag$(D^{(1)}_k, \cdots, D^{(n)}_k)\in\mathbb{R}^{n\times n}, k\in \mathbb{Z_+}.$ Some assumptions are given here:

$(P_1)$ There exists a constant $\omega > 0$ such that $A(t+\omega) = A(t), \ B(t+\omega) = B(t), \ C(t+\omega) = C(t), \ \tau(t+\omega) = \tau(t), \ t\in \mathbb{R}_+;$

$(P_2)$ For a given $\omega > 0$, there exists a constant $q\in \mathbb{Z}_+$ such that $t_{k+q} = t_k+\omega, \ D_{k+q} = D_{k}, \ t\in \mathbb{R}_+, \ k\in \mathbb{Z}_+;$

$(P_3)$ $D^{(i)}_k\in(0, 1), \ i\in \Lambda, \ k\in \mathbb{Z}_+;$

$(P_4)\ a^\star_{ii} = \sup_{t\in [0, \omega]} a_{ii}(t), \ a^\star_{ij} = \sup_{t\in [0, \omega]} |a_{ij}(t)| (i\neq j), \ b^\star_{ij} = \sup_{t\in [0, \omega]} |b_{ij}(t)|, i, j\in\Lambda.$

Theorem 3.2. Assume that assumptions $(P_1)-(P_4)$ hold. Then Eq (5) admits a stationary oscillation, if there exists a constant $\sigma > 0$ such that $t_k-t_{k-1}\leq \sigma, \ k\in \mathbb{Z}_+, \sup_{i\in\Lambda, k\in \mathbb{Z}_+}D^{(i)}_k < 1$ and

Proof. Note that $f(t, x_t) = B(t)x(t-\tau(t))+ C(t)$ implies that $L_{ij} = b_{ij}, i, j\in \Lambda.$ By Theorem 3.1, the above result can be derived directly. □

Furthermore, we consider the well-known single species logarithmic population model with impulses (see ^[25,26]):

where $x$ denotes the size of population. Here $\gamma(t)$ is the growth rate. While there are plenty of resources and there is no intra-specific competition for these resources, $a_1(t)$ is the measure of the competition among the individuals, $a_2(t)$ is added to generalize the model with the same interpretation of competitive effects and $\tau(t)$ is a maturation delay in the sense that competition involves adults who have matured by an age of $\tau(t)$ units, $d_k$ represents the change exponent of population due to some impulsive factors such as human harvesting, weather change, birth pulse and natural enemies at some time $t_k,$ where $t_k$ represent the instants at which the population suffers those rapid changes.

Remark 3.2. Recently, the existence of periodic solution and an almost periodic solution of Eq (6) with/without impulses have been extensively studied in the literature, see ^[25,26]. However, there is very little work about the periodic solution problem of Eq (6) using impulsive control strategies due to technical difficulty. In the following, we shall give some conditions to guarantee the stationary oscillation of Eq (6) using proper impulsive control strategies. First, we need some assumptions as follows:

$(S_1)$ $\gamma, a_1, a_2, \tau\in PC(\mathbb{R}_+, \mathbb{R}_+)$ and moreover there exists a constant $\omega > 0$ such that $\gamma(t+\omega) = \gamma(t), \ a_1(t+\omega) = a_1(t), \ a_2(t+\omega) = a_2(t), \ \tau(t+\omega) = \tau(t), \ t\in \mathbb{R}_+;$

$(S_2)$ For given $\omega > 0$, there exists a constant $q\in \mathbb{Z}_+$ such that $t_{k+q} = t_k+\omega, \ d_{k+q} = d_{k}, \ t\in \mathbb{R}_+, \ k\in \mathbb{Z}_+;$

$(S_3)$ $d_k\in(0, 1), \ k\in \mathbb{Z}_+;$

$(S_4)\ \ a^\star_{1} = \inf_{t\in [0, \omega]} a_{1}(t), \ a^\star_{2} = \sup_{t\in [0, \omega]} a_{2}(t);$

$(S_5)$ The initial value $\phi\in C([-\tau, 0], \mathbb{R}_+),$ where $\tau = \sup_{t\in [0, \omega]} \tau(t).$

Lemma 3.1. Assume that $(S_5)$ holds. Then every solution of Eq (6) is positive on $[t_0, \infty).$

Proof. From Eq (6), we easily get

where

Since $x(t_0) = \phi(0)\in C([-\tau, 0], \mathbb{R}_+),$ it is clear that $x(t) > 0$ for $t\in [t_0, t_1).$ Note that $x(t_1) = [x(t^-_1)]^{d_1}$ implies that $x(t_1) > 0.$ By the same way, we get $x(t) > 0$ for $t\in [t_1, t_2).$ Hence, it can be deduced that $x(t) > 0$ for $t\in [t_0, \infty).$ The proof is complete. □

Based on Lemma 3.1, we can make a transformation $y(t) = \ln x(t),$ which leads to a new system:

Obviously, Eq (6) has a positive stationary oscillation if and only if Eq (7) has a stationary oscillation.

Theorem 3.3. Assume that assumptions $(S_1)-(S_5)$ hold. Then Eq (6) admits a positive stationary oscillation, if there exists a constant $\sigma > 0$ such that $t_k-t_{k-1}\leq \sigma, \ k\in \mathbb{Z}_+, \sup_{k\in \mathbb{Z}_+}d_k < 1$ and

Proof. By Theorem 3.2, the above result can be derived directly. □

4.   Applications

In this section, we employ three examples and their simulations to demonstrate the effectiveness of the obtained results.

Example 4.1. Consider the following simple impulsive delay differential equations:

where $x\in \mathbb{R}, \omega > 0$ and $\rho\in(0, 1)$ are two real constants.

Property 4.1. Equation (8) admits a stationary oscillation if there exists constants $\sigma > 0$ and $q\in \mathbb{Z}_+$ such that

Proof. Note that Eq (8) is $\omega$-periodic, by Theorem 3.1 we can obtain above result easily. □

Corollary 4.1. Equation (8) admits a stationary oscillation with $t_k = \sigma k, k\in \mathbb{Z}_+$ if there exists a constant $\sigma > 0$ such that

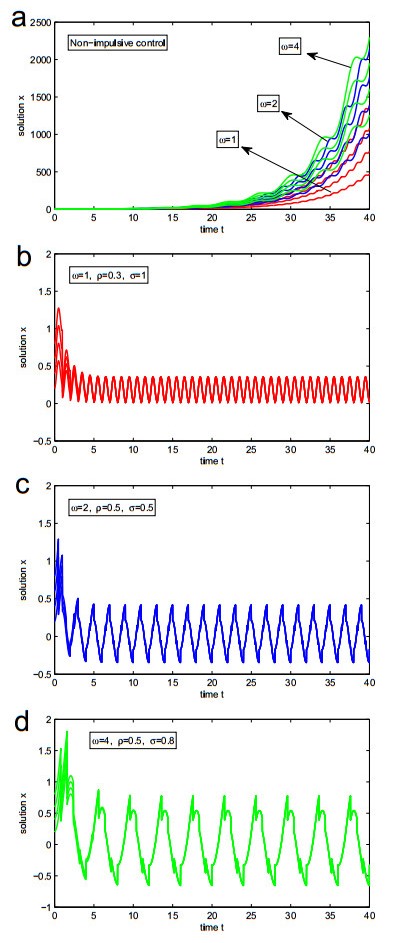
Remark 4.1. In particular, when there is no impulsive effect, i.e., $\rho = 1,$ Eq (8) has no stationary oscillation and moreover it is divergent, which is shown in Figure 1(a) for the case $\omega$ = 1, 2 and 4. Considering impulsive control, for instance, when $\omega = 1,$ one may choose $\rho = 0.3$ and $\sigma = 1$ such that the conditions in Corollary 4.1 hold. Then Eq (8) admits a stationary oscillation with $t_k = k, k\in \mathbb{Z}_+,$ which is shown in Figure 1(b). Additionally, when $\omega = 2$ or 4, one may choose different $\rho$ and $\sigma$ such that Eq (8) admits a stationary oscillation with $t_k = \sigma k, k\in \mathbb{Z}_+$ under the help of Corollary 4.1. The corresponding numerical simulations are shown in Figure 1(c, d). Those simulations results match our development method in this paper perfectly.

Example 4.2. Consider a two-dimensional impulsive delay differential equations:

with

where $\omega > 0$ and $d_1, d_2\in(0, 1)$ are some real constants.

Property 4.2. Eq (9) admits a stationary oscillation if there exists constants $\sigma > 0$ and $q\in \mathbb{Z}_+$ such that

Proof. Note that Eq (9) is $\omega$-periodic, by Theorem 3.2 we can obtain above result directly. □

Corollary 4.2. Eq (9) admits a stationary oscillation with $t_k = \sigma k, k\in \mathbb{Z}_+$ if there exists a constant $\sigma > 0$ such that

Remark 4.2. When there is no impulsive effect, i.e., $d_1 = d_2 = 1,$ Eq (9) has no stationary oscillation and moreover it is divergent, which is shown in Figure 2(a, b). Considering impulsive control, for instance, when $\omega = 1,$ one may choose $d_1 = d_2 = 0.5$ and $\sigma = 1$ such that the conditions in Corollary 4.2 hold. Then Eq (9) admits a stationary oscillation with $t_k = k, k\in \mathbb{Z}_+,$ which is shown in Figure 2(c, d). Additionally, when $\omega = 6,$ the numerical simulations are shown in Figure 3(a-d), where $d_1 = 0.3, d_2 = 0.25$ and $\sigma = 0.6.$ From those simulations, we can see that the proper impulsive control strategies may stabilize the divergent system and make it admit a stationary oscillation.

Example 4.3. Consider a logarithmic population model:

where $x\in \mathbb{R}$ and $d\in(0, 1)$ are two real constants.

Property 4.3. Eq (10) admits a positive stationary oscillation if there exist constants $\sigma > 0$ and $q\in \mathbb{Z}_+$ such that

Corollary 4.3. Eq (10) admits a positive stationary oscillation with $t_k = \sigma k, k\in \mathbb{Z}_+$ if there exists a constant $\sigma > 0$ such that

Remark 4.3. One may observe that Eq (10) has no stationary oscillation when there is no impulsive effect, which is shown in Figure 4(a, b). However, if we take $d = 0.5$ and $\sigma = 0.4$ such that the conditions in Corollary 4.3 hold. Then Eq (10) admits a positive stationary oscillation with $t_k = 0.4k, k\in \mathbb{Z}_+,$ which is shown in Figure 4(c, d).

Appendix. In the simulations, we choose the time step $h = 0.01$ and the initial values $\phi = 0.2m$ in Example 4.1, $\phi = (-0.2m, m)^T$ in Example 4.2 and $\phi = 0.5m$ in Example 4.3, where $m = 1, \cdots, 4.$

5.   Conclusions

This paper was dedicated to the problem of stationary oscillation for a class of nonlinear delay systems with impulses. By using inequality techniques, some new sufficient conditions ensuring the existence of stationary oscillation have been presented. As an application, we have investigated a special system, i.e., single species logarithmic population model. Unlike all methods considered in the literature, our results show that delay systems may admit a stationary oscillation via proper impulsive control strategies even if it was originally unstable or divergent. Three examples with their computer simulations have been provided to demonstrate the feasibility of our control method.

Conflict of interest

All authors declare no conflicts of interest in this paper.