Stochastic persistence and global attractivity of a two-predator one-prey system with S-type distributed time delays

1.   Introduction

In 1977 and 1984, Freedman and Waltman (^[1,2]) studied the following two-predator one-prey system:

where $x_{i}(t)$ stands for the size of the $i$th population and all the parameters are positive constants.

However, the deterministic system has its limitation in mathematical modeling of ecosystems since the parameters involved in the system are unable to capture the influence of environmental noises ^[3,4,5]. Therefore, it is of enormous importance to study the effects of environmental noises on the dynamics of population systems. Assume that the parameters $r_{i}$ are affected by white noises, i.e., $r_{1} \hookrightarrow r_{1}+\sigma_{1}\dot{B}_{1}(t)$, $-r_{2} \hookrightarrow -r_{2}+\sigma_{2}\dot{B}_{2}(t)$, $-r_{3} \hookrightarrow -r_{3}+\sigma_{3}\dot{B}_{3}(t)$, where $B_{i}(t)$ are mutually independent standard Wiener processes defined on a complete probability space $(\Omega, \mathcal{F}, P)$ with a filtration $\{\mathcal{F}_{t}\}_{t\geq 0}$ satisfying the usual conditions. Then, the stochastic two-predator one-prey system with white noises can be expressed as follows:

On the other hand, "all species should exhibit time delay" in the real world, and incorporating time delays in biological systems makes the systems much more realistic than those without time delays (^[6,7,8,9,10]). Hence, in this paper we concern the dynamics of the following stochastic two-predator one-prey system with S-type distributed time delays:

where $\mathcal{D}_{ji}(x_{i})(t) = a_{ji}x_{i}(t)+\int_{-\tau_{ji}}^{0}x_{i}(t+\theta){\mathrm{d}}\mu_{ji}(\theta)$, $\int_{-\tau_{ji}}^{0}x_{i}(t+\theta){\mathrm{d}}\mu_{ji}(\theta)$ are Lebesgue-Stieltjes integrals, $\tau_{ji} > 0$ are time delays, $\mu_{ji}(\theta)$ are nondecreasing bounded variation functions defined on $[-\tau, 0]$, $\tau = \max_{i, j = 1, 2, 3}\left\{\tau_{ji}\right\}$.

2.   Persistence in mean and Extinction

Denote $A_{ij} = a_{ij}+\int_{-\tau_{ij}}^{0}{\mathrm{d}}\mu_{ij}(\theta)$, $D_{1} = r_{1}-\frac{\sigma_{1}^{2}}{2}$, $D_{i} = r_{i}+\frac{\sigma_{i}^{2}}{2}$ $(i = 2, 3)$ and

Assume that $\Theta > 0$. For the matrix corresponding to $\Theta$ (respectively, $\Theta_{k}$), denote by ${\mathrm{M}}_{ij}^{\Theta}$ (respectively, ${\mathrm{M}}_{ij}^{\Theta_{k}}$) the complement minor of the element at the $i$-th row and the $j$-th column $(i, j, k = 1, 2, 3)$.

Theorem 2.1. For any $(\xi_{1}, \xi_{2}, \xi_{3})^{{\mathrm{T}}} \in C([-\tau, 0], \mathbb{R}_{+}^{3})$, system (1.3) has a unique global solution $(x_{1}(t), x_{2}(t), x_{3}(t))^{{\mathrm{T}}} \in \mathbb{R}_{+}^{3}$ on $t \in [0, +\infty)$ a.s. Moreover, for any constant $p > 0$, there are $K_{i}(p) > 0$ such that

Proof. The proof is rather standard and here is omitted (see, e.g., ^[11] and ^[12]).

Lemma 2.1. (^[13]) Suppose $Z(t)\in \mathcal{C}(\Omega\times [0, +\infty), \mathbb{R}_{+})$ and $\lim_{t\rightarrow +\infty}\frac{o(t)}{t} = 0$.

$\mathfrak{(i)}$ If there exists constant $\delta_{0} > 0$ such that for $t \gg 1$,

then

$\mathfrak{(ii)}$ If there exist constants $\delta > 0$ and $\delta_{0} > 0$ such that for $t \gg 1$,

then

Lemma 2.2. Consider the following auxiliary system:

$\mathfrak{(a)}$ If $D_{1} < 0$, then $\lim_{t \rightarrow +\infty}X_{i}(t) = 0$ a.s. $(i = 1, 2, 3)$.

$\mathfrak{(b)}$ If $D_{1} \geq 0$, $-D_{i}+A_{i1}\frac{D_{1}}{A_{11}} < 0$, then

$\mathfrak{(c)}$ If $D_{1} \geq 0$, $-D_{i}+A_{i1}\frac{D_{1}}{A_{11}} \geq 0$, then

Proof. By Itô's formula, we have

where

$\mathfrak{Case \, \, (i):}$ $D_{1} < 0$. Then $\lim_{t\rightarrow +\infty}X_{1}(t) = 0$ a.s. Hence, for $\forall \epsilon \in \left(0, \tfrac{D_{i}}{2}\right)$ and $t \gg 1$,

So, $\lim_{t \rightarrow +\infty}X_{i}(t) = 0$ a.s. $(i = 2, 3)$.

$\mathfrak{Case \, \, (ii):}$ $D_{1} \geq 0$. Then,

Consider the following SDDE:

Then, $X_{i}(t) \leq \widetilde{X_{i}(t)}$ a.s. $(i = 2, 3)$. By Itô's formula,

In view of Lemma 2.1, we obtain:

$(1)^{\dagger}$ If $D_{1} \geq 0$, $-D_{i}+A_{i1}\frac{D_{1}}{A_{11}} < 0$, then $\lim_{t \rightarrow +\infty} \widetilde{X_{i}(t)} = 0$ a.s. $(i = 2, 3)$.

$(2)^{\dagger}$ If $D_{1} \geq 0$, $-D_{i}+A_{i1}\frac{D_{1}}{A_{11}} \geq 0$, then

Therefore, for arbitrary constant $\gamma > 0$,

Based on (2.10) and system (2.7), for $i = 2, 3$,

Thanks to Lemma 2.1, we obtain:

$(1)^{‡}$ If $D_{1} \geq 0$, $-D_{i}+A_{i1}\frac{D_{1}}{A_{11}} < 0$, then $\lim_{t \rightarrow +\infty} X_{i}(t) = 0$ a.s. $(i = 2, 3)$.

$(2)^{‡}$ If $D_{1} \geq 0$, $-D_{i}+A_{i1}\frac{D_{1}}{A_{11}} \geq 0$, then

Therefore, the desired assertion $\mathfrak{(b)}$ follows from combining (2.9) with $(1)^{‡}$, and $\mathfrak{(c)}$ follows from combining (2.9) with $(2)^{‡}$.

Lemma 2.3. For system (1.3), $\limsup_{t \rightarrow +\infty} t^{-1} \ln x_{i}(t) \leq 0$ a.s. $(i = 1, 2, 3)$.

Proof. Thanks to Lemma 2.2 and (2.7), system (2.6) satisfies $\lim_{t \rightarrow +\infty}t^{-1}\ln X_{i}(t) = 0$ a.s. $(i = 1, 2, 3)$. From the stochastic comparison theorem, we obtain the desired assertion.

Theorem 2.2. For system (1.3):

$\mathfrak{(i)}$ If $D_{1} < 0$, then $\lim_{t \rightarrow +\infty}x_{i}(t) = 0$ a.s. $(i = 1, 2, 3)$.

$\mathfrak{(ii)}$ If $D_{1} \geq 0$, ${\mathrm{M}}_{33}^{\Theta_{2}} < 0$, ${\mathrm{M}}_{22}^{\Theta_{3}} < 0$, then

$\mathfrak{(iii)}$ If $D_{1} \geq 0$, ${\mathrm{M}}_{13}^{\Theta} \leq 0$, $\Theta_{3} < 0$, ${\mathrm{M}}_{33}^{\Theta_{2}} > 0$, then

$\mathfrak{(iv)}$ If $\Theta_{1} > 0$, $\Theta_{2} > 0$, $\Theta_{3} > 0$, $M_{11}^{\Theta} > 0$, then

$\mathfrak{(v)}$ If $D_{1} \geq 0$, ${\mathrm{M}}_{12}^{\Theta} \geq 0$, $\Theta_{2} < 0$, $M_{22}^{\Theta_{3}} < 0$, then

$\mathfrak{(vi)}$ If $D_{1} \geq 0$, ${\mathrm{M}}_{12}^{\Theta} \geq 0$, $\Theta_{2} < 0$, $M_{22}^{\Theta_{3}} \geq 0$, then

Proof. According to (2.10), for arbitrary constant $\gamma > 0$,

By Itô's formula and (2.11), we derive

$\mathfrak{Case \, \, (i)}:$ $D_{1} < 0$. From Lemma 2.2 $\mathfrak{(a)}$, $\lim_{t \rightarrow +\infty}x_{i}(t) = 0$ a.s. $(i = 1, 2, 3)$.

$\mathfrak{Case \, \, (ii)}:$ $D_{1} \geq 0$, ${\mathrm{M}}_{33}^{\Theta_{2}} < 0$, ${\mathrm{M}}_{22}^{\Theta_{3}} < 0$. Based on system (2.12), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

By Lemma 2.1 and the arbitrariness of $\epsilon$, we obtain

Hence, for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

According to Lemma 2.1 and the arbitrariness of $\epsilon$, we have

Based on (2.16) and system (2.12), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

In view of Lemma 2.1 and the arbitrariness of $\epsilon$, we obtain

$\mathfrak{Case \, \, (iii)}:$ $D_{1} \geq 0$, ${\mathrm{M}}_{13}^{\Theta} \leq 0$, $\Theta_{3} < 0$, ${\mathrm{M}}_{33}^{\Theta_{2}} > 0$. Compute

By Lemma 2.3, for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

From Lemma 2.1 and the arbitrariness of $\epsilon$, we deduce

By (2.20) and system (2.12), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

According to (2.21), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Thanks to Lemma 2.3, for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

In view of Lemma 2.1 and the arbitrariness of $\epsilon$, we obtain

Thanks to (2.21) and (2.22b), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Based on Lemma 2.1 and the arbitrariness of $\epsilon$, we obtain

Combining (2.22-1) with (2.24) yields

From (2.21) and (2.25), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Thanks to Lemma 2.1 and the arbitrariness of $\epsilon$, we have

Combining (2.22-2) with (2.27) yields

$\mathfrak{Case \, \, (iv)}:$ $\Theta_{1} > 0$, $\Theta_{2} > 0$, $\Theta_{3} > 0$, $M_{11}^{\Theta} > 0$. According to Lemma 2.1, (2.19) and the arbitrariness of $\epsilon$, we obtain

In view of system (2.12), we compute

Then, for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

According to Lemma 2.1 and the arbitrariness of $\epsilon$, we deduce

Therefore, for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Based on (2.31) and system (2.12), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Thanks to Lemma 2.1 and the arbitrariness of $\epsilon$, we obtain

Combining (2.30-1) with (2.33) yields

According to (2.31), (2.33) and system (2.12), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

From Lemma 2.1 and the arbitrariness of $\epsilon$, we have

Combining (2.30-2) with (2.36) yields

Similarly, for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Thanks to Lemma 2.1 and the arbitrariness of $\epsilon$, we obtain

Combining (2.29) with (2.39) yields

$\mathfrak{Case \, \, (v)}:$ $D_{1} \geq 0$, ${\mathrm{M}}_{12}^{\Theta} \geq 0$, $\Theta_{2} < 0$, ${\mathrm{M}}_{22}^{\Theta_{3}} < 0$. By Lemma 2.1, (2.30) and the arbitrariness of $\epsilon$, we have

Hence, for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Based on (2.42), we deduce

Therefore, for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

In view of Lemma 2.1 and the arbitrariness of $\epsilon$, we deduce

According to (2.42) and (2.45), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Clearly, (2.20) is true. From (2.20) and (2.42), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

In view of Lemma 2.1 and the arbitrariness of $\epsilon$, we obtain (2.18).

$\mathfrak{Case \, \, (vi)}:$ $D_{1} \geq 0$, ${\mathrm{M}}_{12}^{\Theta} \geq 0$, $\Theta_{2} < 0$, ${\mathrm{M}}_{22}^{\Theta_{3}} \geq 0$. Thanks to Lemma 2.1, (2.46) and the arbitrariness of $\epsilon$,

According to (2.42) and (2.48), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Based on Lemma 2.1 and the arbitrariness of $\epsilon$, we have

Combining (2.45) with (2.50) yields

By (2.42) and (2.50), for $\forall \epsilon \in (0, 1)$ and $t \gg 1$,

Thanks to Lemma 2.1 and the arbitrariness of $\epsilon$, we deduce

Combining (2.48) with (2.53) yields

The proof is complete.

3.   Global attractivity

Theorem 3.1. Assume that $2 a_{jj} > \sum_{i = 1}^{3}A_{ij}$ $(j = 1, 2, 3)$. Let $X(t; \phi) = : \left(x_{1}(t; \phi), x_{2}(t; \phi), x_{3}(t; \phi)\right)^{{\mathrm{T}}}$ be the solution to system (1.3) with initial condition $\phi \in C([-\tau, 0], \mathbb{R}_{+}^{3})$. Then, for any $\phi$ and $\phi^{*} \in C([-\tau, 0], \mathbb{R}_{+}^{3})$,

Proof. We only need to show

Define

From Itô's formula, we derive

According to (3.3), we have

which implies

Define $G_{i}(t) = \mathbb{E}\left[\left|x_{i}(t; \phi^{*})-x_{i}(t; \phi)\right|\right]$ $(i = 1, 2, 3)$. Then,

Based on Hölder's inequality, for $t_{2} > t_{1}$ and $p > 1$,

In view of Theorem 7.1 in ^[14], for $p \geq 2$, we obtain

From Hölder's inequality, we derive

According to Hölder's inequality, we get

Based on (3.6)-(3.9), for $p \geq 2$ and $|t_{2}-t_{1}| \leq \delta$,

where

Combining (3.5) with (3.10) yields

Therefore, (3.2) follows from (3.4), (3.11) and Barbalat's conclusion in ^[15].

4.   Numerical simulations

In this section we provide some numerical simulations to show the effectiveness of our main theoretical results by using the Milstein approach mentioned in ^[16]. Let $\tau_{ji} = \ln 2$, $\mu_{ji}(\theta) = \mu_{ji}{\mathrm{e}}^{\theta}$. Denote

4.1.   Example 1

Let

subject to $x_{1}(\theta) = 0.7 {\mathrm{e}}^{\theta}$, $x_{2}(\theta) = 0.6 {\mathrm{e}}^{\theta}$, $x_{3}(\theta) = 0.5 {\mathrm{e}}^{\theta}$, $\theta \in [-\ln 2, 0]$.

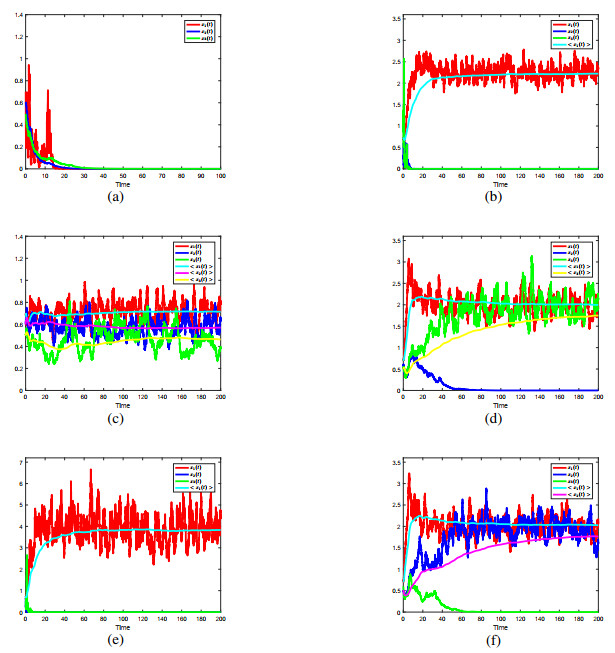
$\bf{Case \, \, 1.}$ $\sigma_{1} = 1.4$, $\sigma_{2} = 0.1$, $\sigma_{3} = 0.1$. Then, $D_{1} = -0.08$. By Theorem 2.2 $\mathfrak{(i)}$, all three species are extinctive. See Figure 1(a).

$\bf{Case \, \, 2.}$ $\sigma_{1} = 0.1$, $\sigma_{2} = 2.0$, $\sigma_{3} = 1.9$. Then, $D_{1} = 0.895$, $M_{33}^{\Theta_{2}} = -0.0745$, $M_{22}^{\Theta_{3}} = -0.046$. From Theorem 2.2 $\mathfrak{(ii)}$, $x_{1}(t)$ is persistent in mean, while $x_{2}(t)$ and $x_{3}(t)$ are extinctive. See Figure 1(b).

$\bf{Case \, \, 3.}$ $\sigma_{1} = 0.1$, $\sigma_{2} = 0.1$, $\sigma_{3} = 0.1$. Then, $\Theta = 0.225$, $\Theta_{1} = 0.16225$, $\Theta_{2} = 0.13375$, $\Theta_{3} = 0.09825$, $M_{11}^{\Theta} = 0.14$. In view of Theorem 2.2 $\mathfrak{(iv)}$, all three species are persistent in mean. See Figure 1(c).

4.2.   Example 2

Let

subject to $x_{1}(\theta) = 0.7 {\mathrm{e}}^{\theta}$, $x_{2}(\theta) = 0.6 {\mathrm{e}}^{\theta}$, $x_{3}(\theta) = 0.5 {\mathrm{e}}^{\theta}$, $\theta \in [-\ln 2, 0]$.

$\bf{Case \, \, 4.}$ $\sigma_{1} = 0.1$, $\sigma_{2} = 0.1$, $\sigma_{3} = 0.1$. Then, $\Theta = 0.001$, $D_{1} = 0.795$, $M_{12}^{\Theta} = 0.01$, $\Theta_{2} = -0.00975$, $M_{22}^{\Theta_{3}} = 0.1975$. According to Theorem 2.2 $\mathfrak{(vi)}$, both $x_{1}(t)$ and $x_{3}(t)$ are persistent in mean, while $x_{2}(t)$ is extinctive. See Figure 1(d).

$\bf{Case \, \, 5.}$ $\sigma_{1} = 0.2$, $\sigma_{2} = 1.8$, $\sigma_{3} = 1.5$. Then, $\Theta = 0.001$, $D_{1} = 0.78$, $M_{12}^{\Theta} = 0.01$, $\Theta_{2} = -0.0143$, $M_{22}^{\Theta_{3}} = -0.031$. Based on Theorem 2.2 $\mathfrak{(v)}$, $x_{1}(t)$ is persistent in mean, while both $x_{2}(t)$ and $x_{3}(t)$ are extinctive. See Figure 1(e).

4.3.   Example 3

Let

subject to $x_{1}(\theta) = 0.7 {\mathrm{e}}^{\theta}$, $x_{2}(\theta) = 0.5 {\mathrm{e}}^{\theta}$, $x_{3}(\theta) = 0.6 {\mathrm{e}}^{\theta}$, $\theta \in [-\ln 2, 0]$.

$\bf{Case \, \, 6.}$ $\sigma_{1} = 0.1$, $\sigma_{2} = 0.1$, $\sigma_{3} = 0.1$. Then, $\Theta = 0.001$, $D_{1} = 0.795$, $M_{13}^{\Theta} = -0.01$, $\Theta_{3} = -0.00975$, $M_{33}^{\Theta_{2}} = 0.1975$. Thanks to Theorem 2.2 $\mathfrak{(iii)}$, both $x_{1}(t)$ and $x_{2}(t)$ are persistent in mean, while $x_{3}(t)$ is extinctive. See Figure 1(f).

All mentioned above can be confirmed by Figure 1.

Acknowledgement

The work is supported by National Natural Science Foundation of China (No.11901166).

Conflict of interest

The authors declare that there are no conflicts of interest.