Multiple bifurcations of a discrete modified Leslie-Gower predator-prey model

1.   Introduction

Mathematical biology has gradually become one of the hot spots and frontier topics in recent decades. The advent of qualitative and quantitative analysis of biological models has made it possible to move from understanding the underlying mechanisms of principles to analyzing them scientifically. It provides a guarantee for making predictions about some biological phenomena. Analyzing species' interactions is one of the research directions in mathematical biology. Generally, a network of interacting species, called a trophic web, forms a complex structure. Each population of interacting species is affected by the others^[1]. Considering the interaction of two species, when the growth rate of one population increases and the other's decreases, these two species are in a predatory relationship. Within a region, the two species with a predatory relationship may coexist or experience the case of species extinction. These situations are of interest to biologists and mathematicians. Thus they construct predator-prey models to research the predatory relationship.

The general Leslie type predator-prey model is one of the most classical predator-prey models; it has the following form

where $\bar{x}$ is the population of the prey and $\bar{y}$ is the population of the predator. The parameters $r$ and $s$ are intrinsic growth rates for the prey and predator populations, respectively. $k_{1}$ reflects the carrying capacity for prey and $\bar{p}(\bar{x}, \bar{y})$ is the functional response function which represents how the predator deals with changes in the prey. $h\bar{x}$ is the carrying capacity for the predator which is proportional to the available prey.

Different functional response functions $\bar{p}(\bar{x}, \bar{y})$ have various effects on the dynamical properties of system (1.1). The authors of ^[2,3,4] have considered that $\bar{p}(\bar{x}, \bar{y})$ is replaced by Holling type III functional response. The case that $\bar{p}(\bar{x}, \bar{y})$ is Holling type IV functional response has been discussed by the authors of ^[5,6,7]. The authors of ^[8,9] have characterized the case that the functional response function $\bar{p}(\bar{x}, \bar{y})$ is related to the predator and prey populations. In 2003, Aziz-Alaoui and Okiye^[10] modified system (1.1) by introducing Holling type II functional response and predator's other food sources. This model is given as follows:

where $\frac{m\bar{y}}{\bar{x}+n}$ is Holling type II functional response. $h\bar{x}+k_{2}$ is the carrying capacity for the predator population and the term $k_{2}$ stands for other food sources for the predator population. All parameters of this system are positive.

Ever since system (1.2) was proposed, it has attracted many interested researchers. Giné and Valls ^[11] discussed the nonlinear oscillations in system (1.2). Lin and Jiang ^[12] applied $n = \frac{k_{2}}{h}$ to system (1.2), combined with stochastic perturbation. And, Xie et al. ^[13] investigated the case that $n = \frac{k_{2}}{h}$ with the linear harvesting of two species. In particular, Xiang et al. ^[14] applied the following scaling to system (1.2):

and they obtained the following:

where $k = \frac{mh}{r}$, $b = \frac{s}{r}$, $a_{1} = \frac{n}{k_{1}}$ and $a_{2} = \frac{k_{2}}{hk_{1}}$. They analyzed the codimension 2 and 3 bifurcations of system (1.3). Moreover, in their work, a lot of valuable results were found by adding the changing environment.

Besides the well-known continuous models, such as those described in ^[15,16,17], the discrete ones have a profound influence and are equally noteworthy. The discrete systems are more applicable to populations with non-overlapping generations, and they have many unique phenomena in addition to the dynamics corresponding to the continuity. The bifurcation of discrete systems plays a key role. When the bifurcation parameter is slightly perturbed near the critical value, the topology of the discrete system changes. Then, it will exhibit a series of dynamic changes that deserve attention. Especially, the study of the discrete codimension 2 bifurcations is more difficult and should receive attention. In the analysis of codimension 2 bifurcations, two independent coefficients of the difference equation are selected as bifurcation parameters. Crossing the two-dimensional bifurcation curves can cause the occurrence of some corresponding codimension 1 bifurcations. There are many attractive results about the bifurcations in discrete systems, such as those described in ^{[18,19,20,21,22]}. Among them, the authors of ^[21] discretized system (1.2) and analyzed its dynamics, which involved the codimension 1 bifurcations and Marotto's chaos. To the best of our knowledge, there are no works about codimension 2 bifurcations of the discrete form of system (1.2). Thus, this issue is the major research topic of our work.

There are many methods of obtaining the discrete form of continuous systems, such as the Runge-Kutta, Taylor series and linear multistep methods. Although these are higher-accuracy methods, they use more calculations, more past values or derivatives ^[23]. However, the Euler method is a traditional and simple way. In particular, the stability of the Euler integrator is associated with the value of the step size. When the step size of the Euler method is large, it may be possible to obtain dynamics that are very different from those of the original continuous system. Chaos is also related to this artificially induced instability ^[20].

Therefore, we apply the same scaling as in ^[14] to system (1.2) and use the Euler method. Then the following model is obtained:

where $d$ is the step size and all parameters are positive. We provide the stability and bifurcation analysis of system (1.4), and this paper is organized as follows. In Section 2, the existence and local stability of fixed points are investigated mainly through the use of the stability theory and center manifold theorem. In Section 3, we analyze the occurrence of codimension 1 and 2 bifurcations of the interior fixed points, including fold bifurcation, 1:1 and 1:2 strong resonance bifurcations and fold-flip bifurcation. Moreover, the results are demonstrated through numerical analysis in Section 4. A brief conclusion is shown in Section 5.

2.   The existence and stability of fixed points

From the following equations:

it is easy to know that system (1.4) has the trivial fixed point $P_{0}(0, 0)$ and the semitrivial fixed points $P_{1}(1, 0)$, $P_{2}(0, a_{2})$. For the positive fixed points, we have the following assumptions.

$(i)$ If $k, a_{1}, a_{2}\in \bigl\{a_{2} = \frac{(1-k-a_{1})^2+4a_{1}}{4k}, k+a_{1} < 1\bigr\}$, then system (1.4) has a positive fixed point $P_{3}(x_{3}, y_{3}) = \bigl(\frac{1-k-a_{1}}{2}, \frac{1-k-a_{1}+2a_{2}}{2}\bigr)$.

$(ii)$ If $k, a_{1}, a_{2}\in\bigl\{\frac{a_{1}}{k} < a_{2} < \frac{(1-k-a_{1})^2+4a_{1}}{4k}, k+a_{1} < 1 \bigr\}$, then system (1.4) has two positive fixed points $P_{4, 5}(x_{4, 5}, y_{4, 5}) = \biggl(\frac{1-k-a_{1}\mp \sqrt{(1-k-a_{1})^2-4(ka_{2}-a_{1})}}{2},$ $\frac{1-k-a_{1}+2a_{2}\mp \sqrt{(1-k-a_{1})^2-4(ka_{2}-a_{1})}}{2}\biggr)$.

$(iii)$ If $k, a_{1}, a_{2}\in\bigl\{a_{2}\leq\frac{a_{1}}{k}, k+a_{1} < 1\bigr\}$, then system (1.4) has a unique positive fixed point $P_{5}(x_{5}, y_{5})$.

Next, we consider the stability of these fixed points and have the following propositions.

Proposition 1. The fixed point $P_{0}$ is unstable and $P_{1}$ is a saddle.

Proof. $J(P_{0})$ and $J(P_{1})$ are the Jacobian matrices of system (1.4) at $P_{0}$ and $P_{1}$, respectively, where

and

Apparently, the eigenvalues associated with $P_{0}$ satisfy that $|\lambda_{P_{0}, 1}| = 1+d > 1$ and $|\lambda_{P_{0}, 2}| = 1+bd > 1$. $\lambda_{P_{1}, 1} = 1-d$ and $\lambda_{P_{1}, 2} = 1+bd$ are the eigenvalues associated with $P_{1}$, where $\lambda_{P_{1}, 1} < 1$ and $\lambda_{P_{1}, 2} > 1$. Hence, we know that the fixed point $P_{0}$ is unstable and $P_{1}$ is a saddle. □

Proposition 2. If $a_{2} < \frac{a_{1}}{k}$, then the fixed point $P_{2}$ is a saddle. If $a_{2} > \frac{a_{1}}{k}$, then the fixed point $P_{2}$ is stable. And if $a_{2} = \frac{a_{1}}{k}$, then $P_{2}$ is semi-stable from the left.

Proof. The Jacobian matrix of system (1.4) at $P_{2}$ is

$\lambda_{P_{2}, 1} = 1+d-\frac{kda_{2}}{a_{1}}$ and $\lambda_{P_{2}, 2} = 1-bd$ are the associated eigenvalues, where $\lambda_{P_{2}, 2} < 1$. It follows from $a_{2} < (>)\frac{a_{1}}{k}$ that $|\lambda_{P_{2}, 1}| = 1+d-\frac{kda_{2}}{a_{1}} > (<)1$. If $a_{2} < (\text{or} > )\frac{a_{1}}{k}$, then the fixed point $P_{2}$ is a saddle (or stable).

When $a_{2} = \frac{a_{1}}{k}$, let $u_{n} = x_{n}$ and $v_{n} = y_{n}-\frac{a_{1}}{k}$. Thus, system (1.4) become as follows:

Applying the invertible transformation

to system (2.5), we get

where

By the center manifold theorem, we assume that $Y_{n} = \mathcal{h}(X_{n}) = \alpha X^2_{n}+\beta X^3_{n}+\mathscr{O}(|X_{n}|^4)$. And the equation

is ought to be satisfied. Then the coefficients $\alpha = \frac{a_{1}+k-1-bk}{ba_{1}}$ and $\beta = \frac{(3k-bk+2a_{1}-2)(a_{1}+k-1-bk)}{a_{1}b}$ are calculated. Substituting $Y_{n} = \mathcal{h}(X_{n})$ into (2.7), we obtain

Naturally, we conclude that $\mathscr{F}'(0) = 1$ and $\mathscr{F}''(0) = \frac{2d(1-k-a_{1})}{a_{1}} > 0$. Hence, by the theory in ^[24], $P_{2}$ is an unstable fixed point and it is semi-stable from the left. □

Proposition 3. The fixed point $P_{3}$ is non-hyperbolic.

Proof. The Jacobian matrix of system (1.4) at $P_{3}$ is

The associated eigenvalues are $\lambda_{P_{3}, 1} = 1$ and $\lambda_{P_{3}, 2} = \frac{k-1-kd+k^2d+bd-kbd-a_{1}+kda_{1}+bda_{1}}{k-1-a_{1}}$. Therefore, $P_{3}$ is non-hyperbolic. □

In order to obtain the conditions that make the fixed point $P_{5}$ (or $P_{4}$) stable, we emphasize the following lemma first.

Lemma 4. ^[25,26] Let $H(\lambda) = \lambda^{2}+A\lambda+B$, where A and B are two real constants. Suppose that $\lambda_{1}$ and $\lambda_{2}$ are two roots of $H(\lambda) = 0$. Then, the following statements are true.

$(i)$ If $H(1) > 0$, then

$(i.1)$ $|\lambda_{1}| < 1$ and $|\lambda_{2}| < 1$ if and only if $H(-1) > 0$ and $B < 1$;

$(i.2)$ $\lambda_{1} = -1$ and $\lambda_{2}\neq-1$ if and only if $H(-1) = 0$ and $A\neq2$;

$(i.3)$ $|\lambda_{1}| < 1$ and $|\lambda_{2}| > 1$ if and only if $H(-1) < 0$;

$(i.4)$ $|\lambda_{1}| > 1$ and $|\lambda_{2}| > 1$ if and only if $H(-1) > 0$ and $B > 1$;

$(i.5)$ $\lambda_{1}$ and $\lambda_{2}$ are a pair of conjugate complex roots, and $|\lambda_{1}| = |\lambda_{2}| = 1$ if and only if $-2 < A < 2$ and $B = 1$;

$(i.6)$ $\lambda_{1} = \lambda_{2} = -1$ if and only if $H(-1) = 0$ and $A = 2$.

$(ii)$ If $H(1) = 0$, namely, if $1$ is one root of $H(\lambda) = 0$, then the other root $\lambda$ satisfies that $|\lambda| = (<, > )1$ if and only if $B = (<, > )1$.

$(iii)$ If $H(1) < 0$, then $H(\lambda) = 0$ has one root lying in $(1, +\infty)$. Moreover,

$(iii.1)$ the other root $\lambda$ satisfies that $\lambda < ( = )-1$ if and only if $H(-1) < ( = )0$;

$(iii.2)$ the other root $\lambda$ satisfies that $-1 < \lambda < 1$ if and only if $H(-1) > 0$.

Proposition 5. If conditions (2.9)–(2.11) are satisfied, then $P_{5}$ is stable.

Proof. The Jacobian matrix of system (1.4) at $P_{5}$ is

According to Lemma 4, we come to the result as follows. If

and

hold, then $P_{5}$ is stable. □

Remark. The example with specific parameters given in Section 4 can intuitively illustrate this proposition. The conditions for $P_{4}$ stability are similar, so we omit them.

3.   Bifurcation analysis

3.1.   Bifurcations at $P_{3}$

In this subsection, we discuss the codimension 1 and 2 bifurcations at $P_{3}$. The coefficients that are not listed explicitly in Subsection 3.1 will be given in Appendices A, B and C.

First, we focus on the case that $b\neq\frac{-k(a_{1}+k-1)}{1-k+a_{1}}$ and $b\neq\frac{2}{d}-\frac{k(a_{1}+k-1)}{1-k+a_{1}}$, i.e., $|\lambda_{P_{3}, 1}| = 1$ and $|\lambda_{P_{3}, 2}|\neq1$. We derive the following theorem about the codimension 1 bifurcation of $P_{3}$.

Theorem 6. If $b\neq\frac{-k(a_{1}+k-1)}{1-k+a_{1}}$ and $b\neq\frac{2}{d}-\frac{k(a_{1}+k-1)}{1-k+a_{1}}$, then system (1.4) undergoes a fold bifurcation at $P_{3}$.

Proof. $a_{2}$ is chosen as the bifurcation parameter and a new variable. Let $a_{2} = \frac{(1-k-a_{1})^2+4a_{1}}{4k}+a^*_{f}$, where $a^*_{f}$ is a sufficiently small perturbation. Then we transform $P_{3}$ into $(0, 0)$ by taking $U_{n} = x_{n}-x_{3}$ and $V_{n} = y_{n}-y_{3}$. Thus, system (1.4) can be expanded at the origin and we obtain the following form

where

Denote $Q = \frac{dk(a_{1}+k-1)}{1-k+a_{1}}$ and $\lambda_{2} = \frac{k-1-kd+k^2d+bd-kbd-a_{1}+kda_{1}+bda_{1}}{k-1-a_{1}}$. Applying the following invertible transformation to system (3.1):

then we have

where

According to the center manifold theorem, $Y_{f, n} = \mathscr{H}(X_{f, n}, a_{f}) = \mathcal{h}_{1}X^2_{f, n}+\mathcal{h}_{2}X_{f, n}a_{f}+\mathcal{h}_{3}a^2_{f}+\mathscr{O}((|X_{f, n}|+|a_{f}|)^3)$ is assumed and the equation

should be satisfied. We calculate that $\mathcal{h}_{1} = 0$, $\mathcal{h}_{2} = \frac{\check{b}_{1}}{1-\lambda_{2}}$ and $\mathcal{h}_{3} = \frac{\check{b}_{3}(1-\lambda_{2})}{(1-\lambda_{2})^2+\check{b}_{1}}$. Then substituting $Y_{f, n} = \mathscr{H}(X_{f, n}, a_{f})$ into (3.3), we attain

Naturally, $\bar{\mathscr{F}}(0, 0) = 0$, $\frac{\partial\bar{\mathscr{F}}}{\partial X_{f, n}}(0, 0) = 1$, $\frac{\partial\bar{\mathscr{F}}}{\partial a_{f}}(0, 0) = 1$ and $\frac{\partial^2\bar{\mathscr{F}}}{\partial X^2_{f, n}}(0, 0) = \frac{2d(a_{1}+k-1)}{1-k+a_{1}}\neq0$ are calculated. Hence, system (1.4) undergoes a fold bifurcation at $P_{3}$. □

When $b = \frac{-k(a_{1}+k-1)}{1-k+a_{1}}$ or $b = \frac{2}{d}-\frac{k(a_{1}+k-1)}{1-k+a_{1}}$, the eigenvalues corresponding to $P_{3}$ satisfy that $|\lambda_{P_{3}, 1}| = |\lambda_{P_{3}, 2}| = 1$. Therefore, we next investigate the codimension 2 bifurcations at $P_{3}$ in Theorems 7 and 8.

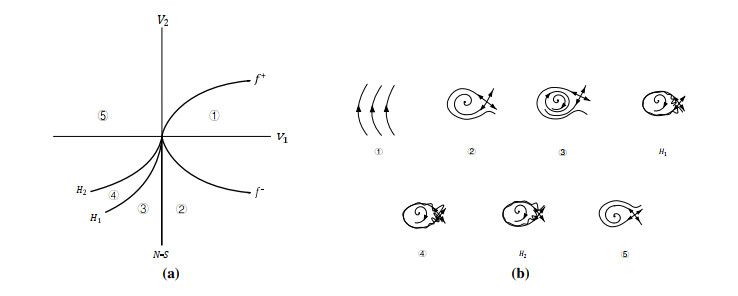
Theorem 7. If the conditions $(k-1)^2\neq a_{1}(3k-1), a_{1}(a_{1}+4k)$ and $det D_{\gamma}V(0)\neq0$ hold, then system (1.4) undergoes a 1:1 strong resonance bifurcation at $P_{3}$. Denote that $\gamma = \{b^*_{R1}, a^*_{R1}\}$ and $\{b, a_{2}\}$ is a small neighborhood of $\{b_{R1}, a_{R1}\}$, where $b = b_{R1}+b^*_{R1}$, $a_{2} = a_{R1}+a^*_{R1}$, $b_{R1} = \frac{-k(a_{1}+k-1)}{1-k+a_{1}}$ and $a_{R1} = \frac{(1-k-a_{1})^2+4a_{1}}{4k}$. When $|\gamma|$ is sufficiently small, the following local dynamics exist:

$1)$ There is a fold bifurcation that occurs on

in the $\gamma$-space.

$2)$ For one of the fixed points born at the fold bifurcation of $1)$, there is a Neimark-Sacker bifurcation that occurs on

in the $\gamma$-space. Moreover, the invariant closed curve of the Neimark-Sacker bifurcation is attracting (repelling) if

$3)$ There is a homoclinic bifurcation at which the stable and unstable manifolds of the saddle point born at the fold bifurcation of $1)$ occurs on two curves $H_{1, 2}$ and has the asymptotic form:

in the $\gamma$-space. The distance between two homoclinic bifurcation curves $H_{1, 2}$ is exponentially small with regard to $\sqrt{|\gamma|}$.

The above-described curves and phase portraits are shown schematically in Figure 1.

Proof. Let $b = b_{R1}+b^*_{R1}$, $a_{2} = a_{R1}+a^*_{R1}$, $\bar{u}_{n} = x_{n}-x_{3}$ and $\bar{v}_{n} = y_{n}-y_{3}$; then, we can expand system (1.4) at $(0, 0)$ as follows

where

Denote that $Q = \frac{dk(a_{1}+k-1)}{1-k+a_{1}}$ and $J_{R1}(\gamma)$ is the Jacobian matrix of system (3.4) at the origin. When $b^*_{R1} = a^*_{R1} = 0$, the two eigenvalues of $J_{R1}(0)$ are $\bar{\lambda}_{1} = \bar{\lambda}_{2} = 1$. We can select the following linearly independent eigenvectors (generalized eigenvectors):

which satisfy the following equations

where the symbol $\langle *, *\rangle$ stands for the standard scalar product in $\mathbb{R}^2$. Then, we can construct the invertible transformation

to simplify the linear part of system (3.4). And, the following equations are deduced:

Under these new coordinates, system (3.4) becomes

where

and $\bar{a}_{00}(0) = \bar{a}_{10}(0) = \bar{a}_{01}(0) = \bar{b}_{00}(0) = \bar{b}_{10}(0) = \bar{b}_{01}(0) = 0$.

According to Lemma 9.6 ^[27], system (3.8) can be written in the following form if $|\gamma|$ is sufficiently small:

where $\varphi^1_{\gamma}(\bar{l}_{n}, \bar{m}_{n})$ is the flow of the planar system

where

Especially, $\bar{c}_{00}(0) = \bar{c}_{10}(0) = \bar{c}_{01}(0) = \bar{d}_{00}(0) = \bar{d}_{10}(0) = \bar{d}_{01}(0) = 0$.

By calculation, the nondegeneracy condition $\bar{d}_{20}(0) = \bar{b}_{20}(0) = 2dQ-\frac{4da_{1}(1+k+a_{1})Q}{(1-k+a_{1})^2}\neq0$ is equal to

And, the following equivalence relationship is deduced:

Suppose that conditions (3.11) and (3.12) hold. According to Lemma 3.2 ^[28], we get the new system

by applying the analytic changes of coordinates and a scaling of time to system (3.10), where $s = sign[\bar{d}_{20}(0)(\bar{c}_{20}(0)+\bar{d}_{11}(0))] = \pm 1$ and

Further, a series of complex calculations provide that

If conditions (3.11) and (3.12) and the transversality condition $det D_{\gamma}V(0)\neq0$ hold, then system (3.13) is the versal unfolding of the Bogdanov-Takens singularity of codimension 2. Referring to Proposition 3.1 ^[28], the existence of 1:1 strong resonance bifurcation of system (1.4) is obtained. □

Theorem 8. Assume that $d\neq\frac{2(1-k+a_{1})}{k(a_{1}+k-1)}$ and $d\neq \frac{a_{1}(k+4+4a_{1})}{2k(a_{1}^2-(k-1)^2)}$. The fold-flip bifurcation of system (1.4) occurs at $P_{3}$ when $\{b, a_{2}\}$ varies in a sufficiently small neighborhood of $\{b_{ff}, a_{ff}\}$, where $b_{ff} = \frac{2}{d}-\frac{k(a_{1}+k-1)}{1-k+a_{1}}$ and $a_{ff} = \frac{(1-k-a_{1})^2+4a_{1}}{4k}$. Furthermore, there are the following local dynamical behaviors taking place:

$1)$ There exists a nondegenerate fold bifurcation on the curve $(\hat{X}, \ \hat{Y}, \ \alpha_{1}) = \Bigl(\frac{-\alpha_{2}}{\hat{A}(0)}+\mathscr{O}\bigl(\alpha^2_{2}\bigr), \ 0, \ \frac{\alpha^2_{2}}{2\hat{A}(0)+\mathscr{O}\bigl(\alpha^3_{2}\bigr)}\Bigr)$.

$2)$ There exists a nondegenerate flip bifurcation on the curve $(\hat{X}, \ \hat{Y}, \ \alpha_{1}) = (0, \ 0, \ 0)$.

$3)$ If $\hat{B}(0) > 0$, $\alpha_{1} < 0$ and $(\hat{A}(0))^2\hat{B}(0)+3\hat{A}(0)\hat{B}(0)+\hat{A}(0)\hat{D}(0)-\hat{B}(0)\hat{C}(0)\neq0$, then there exists a nondegenerate Neimark-Sacker bifurcation of the second iteration of system (3.17) on the curve $(\hat{X}, \ \hat{Y}, \ \alpha_{2}) = \Bigl(0, \ \sqrt{\frac{-2\alpha_{1}}{\hat{B}(0)}}+\mathscr{O}\bigl(\alpha^\frac{2}{3}_{1}\bigr), \ \frac{\alpha^2_{1}(\hat{D}(0)+2\hat{B}(0))}{\hat{B}(0)}+\mathscr{O}\bigl(\alpha^2_{1}\bigr)\ \Bigr)$.

Proof. We select $b$ and $a_{2}$ as bifurcation parameters. Denote $b = b_{ff}+b^*_{ff}$, $a_{2} = a_{ff}+a^*_{ff}$ and $\mu = \{a^*_{ff}, b^*_{ff}\}$. By the transformations $\hat{u}_{n} = x_{n}-x_{3}$ and $\hat{v}_{n} = y_{n}-y_{3}$, system (1.4) can be rewritten in the following form

where

Define that $J_{ff}(\mu)$ is the Jacobian matrix of system (3.15) at $(0, 0)$. Then, the associated eigenvalues are $\hat{\lambda}_{1}(\mu) = 1$ and

The vectors $\hat{p}_{1}(\mu)\ (\text{or}\ \hat{q}_{1}(\mu))$ and $\hat{p}_{2}(\mu)\ (\text{or}\ \hat{q}_{2}(\mu))$ are the eigenvectors of $J_{ff}(\mu)\ (\text{or}\ J^T_{ff}(\mu))$ belonging to the eigenvalues $\hat{\lambda}_{1}(\mu)$ and $\hat{\lambda}_{2}(\mu)$, respectively, such that $J_{ff}(\mu)\hat{p}_{1}(\mu) = \lambda_{1}(\mu)\hat{p}_{1}(\mu)$, $J_{ff}^T(\mu)\hat{q}_{1}(\mu) = \lambda_{1}(\mu)\hat{q}_{1}(\mu)$, $J_{ff}(\mu)\hat{p}_{2}(\mu) = \lambda_{2}(\mu)\hat{p}_{2}(\mu)$ and $J_{ff}^T(\mu)\hat{q}_{2}(\mu) = \lambda_{2}(\mu)\hat{q}_{2}(\mu)$. By calculation, we can choose a set of vectors

satisfying that $\langle \hat{p}_{1}(\mu), \hat{q}_{1}(\mu)\rangle = \langle \hat{p}_{2}(\mu), \hat{q}_{2}(\mu)\rangle = 1$ and $\langle \hat{p}_{1}(\mu), \hat{q}_{2}(\mu)\rangle = \langle \hat{p}_{2}(\mu), \hat{q}_{1}(\mu)\rangle = 0$, where

For simplification of the linear part of system (3.15), we express $(\hat{u}_{n}, \hat{v}_{n})^T$ as the linear combination of eigenvectors, as follows:

and have the following new coordinates:

Under the coordinates $(\hat{l}_{n}, \hat{m}_{n})^T$, system (3.15) has the following form

where

Assume that $Q = \frac{dk(a_{1}+k-1)}{1-k+a_{1}}\neq2$, i.e., $d\neq\frac{2(1-k+a_{1})}{k(a_{1}+k-1)}$; the coefficients $\hat{c}_{00}(\mu)$, $\hat{d}_{00}(\mu)$, $\hat{\lambda}_{1}(\mu)$ and $\hat{\lambda}_{2}(\mu)$ can be expanded as follows

where

Supposing that $M = 2dQ-\frac{dka_{1}}{(1-k+a_{1})^2}-\frac{4da_{1}(1+a_{1})}{(1-k+a_{1})^2}\neq0$, i.e., $d\neq \frac{a_{1}(k+4+4a_{1})}{2k(a_{1}^2-(k-1)^2)}$, it is easy to obtain that $\hat{d}_{11}(0) = \frac{M}{Q(2-Q)}\neq0$,

and $4\hat{d_{11}}(0)\triangle\neq0$. Therefore, according to Proposition 2.1.3 ^[29], system (3.16) is smoothly equivalent to the following:

where

And considering the critical state, we have

Apparently, $\hat{A}(0)$ and $\hat{B}(0)$ are not equal to zero because $k+a_{1} < 1$.

By the knowledge of the local codimension 1 bifurcation in ^[29] and ^[30], we know the following:

$1)$ If $\hat{A}(0)\neq0$, then there exists a nondegenerate fold bifurcation on the curve $(\hat{X}, \ \hat{Y}, \ \alpha_{1}) = \Bigl(\frac{-\alpha_{2}}{\hat{A}(0)}+\mathscr{O}\bigl(\alpha^2_{2}\bigr), \ 0, \ \frac{\alpha^2_{2}}{2\hat{A}(0)+\mathscr{O}\bigl(\alpha^3_{2}\bigr)}\Bigr)$.

$2)$ If $\hat{B}(0)\neq0$, then there exists a nondegenerate flip bifurcation on the curve $(\hat{X}, \ \hat{Y}, \ \alpha_{1}) = (0, \ 0, \ 0)$.

$3)$ If $\hat{B}(0) > 0$, $\alpha_{1} < 0$ and $(\hat{A}(0))^2\hat{B}(0)+3\hat{A}(0)\hat{B}(0)+\hat{A}(0)\hat{D}(0)-\hat{B}(0)\hat{C}(0)\neq0$, then there exists a nondegenerate Neimark-Sacker bifurcation of the second iteration of system (3.17) on the curve $(\hat{X}, \ \hat{Y}, \ \alpha_{2}) = \Bigl(0, \ \sqrt{\frac{-2\alpha_{1}}{\hat{B}(0)}}+\mathscr{O}\bigl(\alpha^\frac{2}{3}_{1}\bigr), \ \frac{\alpha^2_{1}(\hat{D}(0)+2\hat{B}(0))}{\hat{B}(0)}+\mathscr{O}\bigl(\alpha^2_{1}\bigr)\ \Bigr)$.

We summarize the results in Theorem 8. In addition, the schematic diagrams of bifurcation curves and phase portraits classfied by different values of $\hat{A}(0)$ and $\hat{B}(0)$ can be found on pp. 476–478 in ^[27]. □

3.2.   Bifurcations at $P_{5}$

If $k, a_{1}, a_{2}\in\bigl\{\frac{a_{1}}{k} < a_{2} < \frac{(1-k-a_{1})^2+4a_{1}}{4k}, k+a_{1} < 1 \bigr\}$, then system (1.4) has two positive fixed points $P_{4, 5}(x_{4, 5}, y_{4, 5})$. When $a_{2}$ decreases to $\frac{a_{1}}{k}$ (or is less than it), $P_{4}$ is not positive and system (1.4) has the unique interior fixed point $P_{5}$. Because of the different levels of details, in this work, we consider the bifurcations at $P_{5}$ when $k, a_{1}, a_{2}\in\bigl\{a_{2}\leq\frac{a_{1}}{k}, k+a_{1} < 1\bigr\}$. The coefficients that are not listed explicitly in this subsection will be given in Appendix D.

Theorem 9. Suppose that $2a_{1}(b_{R2}+d)^2-6a_{1}+(b_{R2})^2d^2x_{5}\neq0$, $\tilde{A}_{1}(0)\neq0$ and $\tilde{B}_{1}(0)\neq 0$. If $\{k, b\}$ varies in a sufficiently small neighborhood of $\{k_{R2}, b_{R2}\}$, then system (1.4) undergoes a 1:2 strong resonance bifurcation at $P_{5}$, where

Moreover, the following dynamics take place in system (1.4):

$(i)$ there exists a flip bifurcation curve $\{(s_{1}, s_{2}):s_{1} = 0\}$;

$(ii)$ there exists the nondegenerate Neimark-Sacker bifurcation curve $\{(s_{1}, s_{2}):s_{2} = 0, \ s_{1} < 0\}$;

$(iii)$ there is a heteroclinic bifurcation curve $\{(s_{1}, s_{2}):s_{2} = \frac{-5s_{1}}{3}+\mathit{\text{o}}(s_{1}), \ s_{1} < 0\}$.

Proof. Let $k = k_{R2}+k^*_{R2}$ and $b = b_{R2}+b^*_{R2}$. By taking $\tilde{u}_{n} = x_{n}-x_{5}$ and $\tilde{v}_{n} = y_{n}-y_{5}$, $P_{5}$ is transformed to $(0, 0)$. Then, system (1.4) has the following new form

where $\theta = \{k^*_{R2}, b^*_{R2}\}$. The Jacobian matrix of system (3.18) is

When $k^*_{R2} = b^*_{R2} = 0$, we have

The associated eigenvalues are $\tilde{\lambda}_{1} = \tilde{\lambda}_{2} = -1$. By calculations, we can choose a set of eigenvectors and generalized eigenvectors

such that

Construct the transformation

Then, the new coordinates are given by

Applying (3.19) and (3.20) to system (3.18), we obtain

where

To further simplify the linear part of system (3.21), the following non-singular linear coordinate transformation is applied to this system:

Then, we have the following system:

where

When $k^*_{R2} = 0$ and $b^*_{R2} = 0$, we have

Supposing that $2a_{1}(b^2_{R2}d^2-2)-6a_{1}+(b_{R2})^2d^2x_{5}\neq0$, (3.23) is not equal to zero. It means that the map $\{k^*_{R2}, b^*_{R2}\}\rightarrow \{\tilde{\varepsilon}(\theta), \tilde{\delta}(\theta)\}$ is regular when $k^*_{R2} = b^*_{R2} = 0$. Therefore, we can transform $\theta = \{k^*_{R2}, b^*_{R2}\}$ to $\zeta = \{\zeta_{1}, \zeta_{2}\}$, where $\zeta_{1} = \tilde{\varepsilon}(\theta)$ and $\zeta_{2} = \tilde{\delta}(\theta)$. The perturbations $k^*_{R2}$ and $b^*_{R2}$ can be seen as the functions of $\zeta_{1}$ and $\zeta_{2}$ as follows

where $P_{R2} = \frac{-d^2b_{R2}y_{5}(2a_{1}+x_{5})+2dy_{5}a_{1}}{(x_{5}+a_{1})^2}$, $Q_{R2} = \frac{-dy_{5}a_{1}}{(x_{5}+a_{1})^2}$ and $M_{R2} = \frac{-1}{b_{R2}}$. With $\{\zeta_{1}, \zeta_{2}\}$, system (3.22) can be expressed as

where

According to Lemma 9.8 ^[27], system (3.24) can be rewritten as

where

Obviously, the linear part of system (3.25) is

when $\zeta_{1} = \zeta_{2} = 0$. Because the eigenvalues of matrix (3.26) are negative, it is impossible to approximate system (3.25) by a flow. Hence, we consider the second iteration of this system and get

where

Denote $\rho = \{\tilde{L}_{n}, \tilde{M}_{n}\}^T.$When $||\zeta||$ is sufficiently small, then system (3.27) can be represented by $\Phi_{\zeta}(\rho)+\mathscr{O}(||\rho||^4)$, where $\Phi_{\zeta}(\rho)$ is a flow of the planar system given by

$p(\zeta, \rho)$ is the symbol of homogeneous cubic terms. Moreover, $\Phi_{\zeta}(\rho)+\mathscr{O}(||\rho||^4)$ can be further simplified. The planar system is smoothly equivalent to the following:

where $\eta_{1}(\zeta) = 4\zeta_{1}+\mathscr{O}(||\zeta||^2)$, $\eta_{2}(\zeta) = -2\zeta_{1}-2\zeta_{2}+\mathscr{O}(||\zeta||^2)$, $\tilde{A}_{1}(0) = 4\tilde{A}(0)$ and $\tilde{B}_{1}(0) = -2\tilde{B}(0)-6\tilde{A}(0)$.

If $\tilde{A}_{1}(0), \tilde{B}_{1}(0)\neq0$, the bifurcations of system (3.30) can be analyzed by using the following system:

where $s_{3} = \text{sign}(\tilde{A}_{1}(0))$. By applying the theory in ^[27] and ^[31], we summarize our analysis into Theorem 9. The schematic diagrams of bifurcation curves and phase portraits can be found on pp. 444–446 in ^[27]. □

4.   Numerical analysis

In this section, we use some cases with specific values to explain our theoretical analysis.

4.1.   The example of Proposition 5 with specific parameters

Let $a_{1} = 0.1$, $a_{2} = 0.4$, $k = 0.3$, $b = 1.5$ and $d = 0.7$. We find that the conditions $H(1) = 0.330403 > 0$, $H(-1) = 1.95787 > 0$ and $Det(J(E_{5}))-1 = -0.855866 < 0$ hold. Therefore, $P_{5}(0.564575, 0.964575)$ is the stable interior fixed point of system (1.4). Figure 2 is the time-series diagram of the prey and predator populations. As the number of iterations increases, the populations of both species are constant, which implies that $P_{5}$ is stable.

4.2.   Fold bifurcation

Let $a_{1} = 0.2$, $k = 0.4$, $d = 0.8$ and $b = 0.5$. $a_{2} = 0.6$ is the critical value such that the fold bifurcation of system (1.4) occurs. Figure 3 is the fold bifurcation diagram. By analyzing this diagram, we find that there is no positive fixed point of system (1.4) when $a_{2} > 0.6$. If $a_{2} = 0.6$, there is a unique interior fixed point $P_{3}(0.2, 0.8)$. And if $a_{2} < 0.6$, there are two interior fixed points $P_{4}$ and $P_{5}$ bifurcate from $P_{3}$. According to the eigenvalues of $P_{4}$ and $P_{5}$, we know that $P_{5}$ is stable and $P_{4}$ is unstable.

4.3.   1:1 strong resonance bifurcation

Fixing $d = 0.8$, $k = 0.7$ and $a_{1} = 0.1$. The critical values of the bifurcation parameters are $a_{R1} = 0.15714286$ and $b_{R1} = 0.35$ when $\lambda_{P_{3}, 1} = \lambda_{P_{3}, 2} = 1$. Then we calculate that the conditions $(k-1)^2 = 0.03\neq a_{1}(3k-1) = 0.11$, $(k-1)^2 = 0.03\neq a_{1}(a_{1}+4k) = 0.29$ and $det D_{\gamma}V(0) = -3770.47\neq0$ are satisfied. Hence, system (1.4) undergoes a 1:1 strong resonance bifurcation at $P_{3}(0.1, 0.25714286)$ as $\{b, a_{2}\}$ varies in a small neighborhood of $\{0.35, 0.15714286\}$. The software package MatContM has been applied to confirm our analysis. For more details of this package, ^[32,33] are available for reference. The Neimark-Sacker (NS) and fold (LP) curves are shown in Figure 4(a) and the symbol R1 denotes the 1:1 strong resonance bifurcation point. In Figure 4(b), we plot the phase portrait with $a_{2} = 0.13$ and $b = 0.35$. Based on observation of this subfigure, there exists an invariant closed curve. Figure 4(c) is the time series diagram of the prey $x$ and predator $y$ populations with the same specific parameters as Figure 4(b). The blue and magenta points represent the populations of prey and predator, respectively. Both species exist in periodic oscillations due to the invariant closed curve.

4.4.   Fold-flip bifurcation

Let $d = 0.8$, $k = 0.3$ and $a_{1} = 0.3$. $b = 2.63$ and $a_{2} = 1.13333$ are the critical values of the bifurcation parameters such that $\lambda_{P_{3}, 1} = 1$ and $\lambda_{P_{3}, 2} = -1$. Then, we have that conditions $d\neq\frac{2(1-k+a_{1})}{k(a_{1}+k-1)} = -16.66667$ and $d\neq \frac{a_{1}(k+4+4a_{1})}{2k(a_{1}^2-(k-1)^2)} = -5.75$. By Theorem 8, the fold-flip bifurcation of system (1.4) occurs at $P_{3}(0.2, 1.33333)$ when $\{b, a_{2}\}$ varies in a sufficiently small neighborhood of $\{2.63, 1.13333\}$. Figure 5(a) illustrates our analysis and LPPD is the symbol of the fold-flip bifurcation point. Then, let $a_{2} = 1.15$ and $b = 3.5$. The phase portrait is shown in Figure 5(b). At this point, system (1.4) is in a chaotic state in which the predator and prey populations cannot coexist stably. In Figure 5(c), the positive values of the corresponding maximum Lyapunov exponents also explain the existence of chaos.

4.5.   1:2 strong resonance bifurcation

Suppose that $d = 2.3$, $a_{1} = 0.2$ and $a_{2} = 0.4$. $k_{R2} = 0.336956$ and $b_{R2} = 1.47749$ are the critical bifurcation parameters such that $\tilde{\lambda}_{1} = \tilde{\lambda}_{2} = -1$. The conditions $2a_{1}(b^2_{R2}d^2-2)-6a_{1}+(b_{R2})^2d^2x_{5} = 9.27343\neq0$, $\tilde{A}_{1}(0) = -178.936\neq0$ and $\tilde{B}_{1}(0) = 26.7684\neq0$ hold. According to Theorem 9, the 1:2 strong resonance bifurcation of system (1.4) takes place at $P_{5}(0.576225, 0.976225)$, when $\{k, \ b\}$ varies in a small neighborhood of $\{0.336956, 1.47749\}$. The NS and PD curves are plotted in Figure 6(a) which illustrates the existence of this bifurcation. The symbol R2 stands for the 1:2 strong resonance bifurcation point. In this example, we take the step size of the Euler method as $2.3$. The choice of a large step size changes the dynamical behaviors of the original continuous system. Moreover, we can also find fold-flip and generalized period-doubling bifurcation points in Figure 6(a), where the symbol $GPD$ represents the period-doubling bifurcation point. Figure 6(b) is the phase portrait of $x$ and $y$, when $k = 0.33$ and $b = 1.47$. From this subfigure, we can observe that due to the existence of this bifurcation, the dynamical properties of system (1.4) change in the neighborhood of the critical parameters and produce an invariant closed curve.

Then, select $d$ and $b$ as the bifurcation parameters. Let $k = 0.6$, $a_{1} = 0.2$ and $a_{2} = 0.3$. By numerical simulation, we know that a 1:2 strong resonance bifurcation of system (1.4) exists at $P_{5}(0.27320508, 0.57320508)$ when $\{b, d\}$ varies in a sufficiently small neighborhood of $\{1.0728398, 4.3176514\}$. The PD and NS curves in Figure 6(c) intuitively show the existence of 1:2 strong resonance bifurcation. The critical values of bifurcation parameter $d$ are large which illustrates the effect of step size on the dynamics.

5.   Conclusions

In this paper, we discuss the existence and stability of the fixed points of system (1.4). The bifurcations of system (1.4) have also been investigated and numerical analysis has been used to support our work. We provide an analysis of the codimension 1 and 2 bifurcations at $P_{3}$, including fold, 1:1 strong resonance and fold-flip bifurcations. It demonstrates the abundant dynamics of system (1.4). Further, we have analyzed the existence of 1:2 strong resonance bifurcation at $P_{5}$. And, through examples with specific values, we found that selecting another two independent coefficients as bifurcation parameters does not change the existence of this bifurcation. In addition, the continuation curves are used to show the new dynamical behaviors, including the generalized period-doubling and fold-flip bifurcations at $P_{5}$. For the interior fixed point $P_{4}$, the analysis of bifurcations is similar, so we have omitted the detailed descriptions in this work. The occurrences of these codimension 2 bifurcations imply that system (1.4) undergoes local codimension 1 bifurcations, such as fold, flip, homoclinic and Neimark-Sacker bifurcations. These complex phenomena may lead to the species not being able to coexist in a stable state.

To the best of our knowledge, the content of our analysis for system (1.4) has not been studied. Our work demonstrates that, compared to the continuous system, the dynamical properties of the discrete system are variable. In particular, the dynamics of discrete systems are affected by the choice of a large step size of the Euler method. The difference between continuous and discrete systems is attractive. Additionally, 1:1 strong resonance bifurcation corresponds to Bogdanov-Takens bifurcation in continuous systems. However, generalized period-doubling bifurcation, fold-flip bifurcation and 1:2 strong resonance bifurcation are unique to the discrete system and have many interesting properties. And, the discrete systems can reflect the interactions of species more realistically when the populations of species are small or the processes of birth and death occur at discrete times. Moreover, other codimension 2 bifurcations and the harvesting of species are meaningful topics. We will consider these in the future.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

The second author was supported by the National Natural Science Foundation of China (No. 12001503) and the third author was supported by the Project of Beijing Municipal Commission of Education (KM 202110015001).

Conflict of Interest

The authors declare that they have no conflicts of interest.

Appendix

A.   The coefficients in the proof of Theorem 6

The coefficients of system (3.3) are as follows:

B.   The coefficients in the proof of Theorem 7

1)The coefficients $\bar{a}_{ij}(\gamma)$, $\bar{b}_{ij}(\gamma)$ ($0\leq i+j < 3$) of system (3.8):

2) The coefficients $\bar{c}_{ij}(\gamma)$, $\bar{d}_{ij}(\gamma)$ ($0\leq i+j < 3$) of system (3.10):

3) The coefficients $A_{0}$, $A_{i}(\gamma)$ ($i = 1, 2, 3, 4$) of system (3.13):

C.   The coefficients in the proof of Theorem 8

1) The coefficients $\hat{a}_{ij}(\gamma)$, $\hat{b}_{ij}(\gamma)$ ($0\leq i+j < 4$) of system (3.15):

2) The coefficients $\hat{c}_{00}(\mu)$, $\hat{d}_{00}(\mu)$, $\hat{c}_{ij}(\gamma)$, $\hat{c}_{ij}(\gamma)$ ($2\leq i+j < 4$) of system (3.16):

where

D.   The coefficients in the proof of Theorem 9

1)The coefficients $\tilde{k}_{ij}(\theta)$, $\tilde{r}_{ij}(\theta)$ ($1\leq i+j < 4$) of system (3.18)

2)Denote $P_{R2} = \frac{-d^2b_{R2}y_{5}(2a_{1}+x_{5})+2dy_{5}a_{1}}{(x_{5}+a_{1})^2}$, $Q_{R2} = \frac{-dy_{5}a_{1}}{(x_{5}+a_{1})^2}$ and $M_{R2} = \frac{-1}{b_{R2}}$. The coefficients $\tilde{a}(\theta)$, $\tilde{b}(\theta)$, $\tilde{c}(\theta)$, $\tilde{d}(\theta)$, $\tilde{a}_{ij}(\theta)$, $\tilde{b}_{ij}(\theta)$ ($2\leq i+j < 4$) of system (3.21):

3) The coefficients $\tilde{\varepsilon}(\theta)$, $\tilde{\delta}(\theta)$, $\tilde{c}_{ij}(\theta)$, $\tilde{d}_{ij}(\theta)$ ($2\leq i+j < 4$) of system (3.22):

4) The coefficients $\tilde{g}_{ij}(\zeta)$, $\tilde{h}_{ij}(\zeta)$ ($2\leq i+j < 4$) of system (3.24):