Figure 1.
Elbow joint finite element model.
To enhance the reproducibility of motor unit number index (MUNIX) for evaluating neurological disease progression, this paper proposes a negative entropy-based fast independent component analysis (FastICA) demixing method to assess MUNIX reproducibility in the presence of inter-channel mixing of electromyography (EMG) signals acquired by high-density electrodes. First, composite surface EMG (sEMG) signals were obtained using high-density surface electrodes. Second, the FastICA algorithm based on negative entropy was employed to determine the orthogonal projection matrix that minimizes the negative entropy of the projected signal and effectively separates mixed sEMG signals. Finally, the proposed experimental approach was validated by introducing an interrelationship criterion to quantify independence between adjacent channel EMG signals, measuring MUNIX repeatability using coefficient of variation (CV), and determining motor unit number and size through MUNIX. Results analysis shows that the inclusion of the full (128) channel sEMG information leads to a reduction in CV value by 1.5±0.1 and a linear decline in CV value with an increase in the number of channels. The correlation between adjacent channels in participants decreases by 0.12±0.05 as the number of channels gradually increases. The results demonstrate a significant reduction in the number of interrelationships between sEMG signals following negative entropy-based FastICA processing, compared to the mixed sEMG signals. Moreover, this decrease in interrelationships becomes more pronounced with an increasing number of channels. Additionally, the CV of MUNIX gradually decreases with an increase in the number of channels, thereby optimizing the issue of abnormal MUNIX repeatability patterns and further enhancing the reproducibility of MUNIX based on high-density surface EMG signals.
Citation: Suqi Xue, Farong Gao, Xudong Wu, Qun Xu, Xuecheng Weng, Qizhong Zhang. MUNIX repeatability evaluation method based on FastICA demixing[J]. Mathematical Biosciences and Engineering, 2023, 20(9): 16362-16382. doi: 10.3934/mbe.2023730
| [1] | Huihao Wang, Kuan Wang, Zhen Deng, Xiaofei Li, Yi-Xian Qin, Hongsheng Zhan, Wenxin Niu . Effects of facet joint degeneration on stress alterations in cervical spine C5–C6: A finite element analysis. Mathematical Biosciences and Engineering, 2019, 16(6): 7447-7457. doi: 10.3934/mbe.2019373 |
| [2] | Yan Li, Kuan Wang, Lejun Wang, Tongbo Chang, Shengnian Zhang, Wenxin Niu . Biomechanical analysis of the meniscus and cartilage of the knee during a typical Tai Chi movement—brush-knee and twist-step. Mathematical Biosciences and Engineering, 2019, 16(2): 898-908. doi: 10.3934/mbe.2019042 |
| [3] | Xiaoguang Liu, Jiawei Wang, Tie Liang, Cunguang Lou, Hongrui Wang, Xiuling Liu . SE-TCN network for continuous estimation of upper limb joint angles. Mathematical Biosciences and Engineering, 2023, 20(2): 3237-3260. doi: 10.3934/mbe.2023152 |
| [4] | Chengliang Wu, Weiya Hao, Wei He, Xiaofei Xiao, Xuhong Li, Wei Sun . Biomechanical and neuromuscular strategies on backward somersault landing in artistic gymnastics: A case study. Mathematical Biosciences and Engineering, 2019, 16(5): 5862-5876. doi: 10.3934/mbe.2019293 |
| [5] | Won Man Park, Young Joon Kim, Shaobai Wang, Yoon Hyuk Kim, Guoan Li . Investigation of lumbar spine biomechanics using global convergence optimization and constant loading path methods. Mathematical Biosciences and Engineering, 2020, 17(4): 2970-2983. doi: 10.3934/mbe.2020168 |
| [6] | Xiang Xiao, Huijing Hu, Lifang Li, Le Li . Comparison of dominant hand to non-dominant hand in conduction of reaching task from 3D kinematic data: Trade-off between successful rate and movement efficiency. Mathematical Biosciences and Engineering, 2019, 16(3): 1611-1624. doi: 10.3934/mbe.2019077 |
| [7] | Lin Chen, Mingjun Wang, Zhanyu Wu, Jinbo Sun, Jianglong Li, Chun Chen, Chuan Ye . Advancements in health informatics: finite element insights into medial open-wedge high tibial osteotomy and lateral meniscal tears. Mathematical Biosciences and Engineering, 2024, 21(4): 5394-5410. doi: 10.3934/mbe.2024237 |
| [8] | Linxuan Zhou, Jingwei Gao, Qiao Li, Cheng Hu . Simulation study on tractive performance of off-road tire based on discrete element method. Mathematical Biosciences and Engineering, 2020, 17(4): 3869-3893. doi: 10.3934/mbe.2020215 |
| [9] | Zhizhou Ma, Yujun Qi, Weiqing Liu . A comparative study of pull-out performance of bolted joints in pultruded FRP with drilled holes or punched holes. Mathematical Biosciences and Engineering, 2019, 16(5): 4213-4228. doi: 10.3934/mbe.2019210 |
| [10] | Zhigao Zeng, Changjie Song, Qiang Liu, Shengqiu Yi, Yanhui Zhu . Diagnosis of musculoskeletal abnormalities based on improved lightweight network for multiple model fusion. Mathematical Biosciences and Engineering, 2024, 21(1): 582-601. doi: 10.3934/mbe.2024025 |
To enhance the reproducibility of motor unit number index (MUNIX) for evaluating neurological disease progression, this paper proposes a negative entropy-based fast independent component analysis (FastICA) demixing method to assess MUNIX reproducibility in the presence of inter-channel mixing of electromyography (EMG) signals acquired by high-density electrodes. First, composite surface EMG (sEMG) signals were obtained using high-density surface electrodes. Second, the FastICA algorithm based on negative entropy was employed to determine the orthogonal projection matrix that minimizes the negative entropy of the projected signal and effectively separates mixed sEMG signals. Finally, the proposed experimental approach was validated by introducing an interrelationship criterion to quantify independence between adjacent channel EMG signals, measuring MUNIX repeatability using coefficient of variation (CV), and determining motor unit number and size through MUNIX. Results analysis shows that the inclusion of the full (128) channel sEMG information leads to a reduction in CV value by 1.5±0.1 and a linear decline in CV value with an increase in the number of channels. The correlation between adjacent channels in participants decreases by 0.12±0.05 as the number of channels gradually increases. The results demonstrate a significant reduction in the number of interrelationships between sEMG signals following negative entropy-based FastICA processing, compared to the mixed sEMG signals. Moreover, this decrease in interrelationships becomes more pronounced with an increasing number of channels. Additionally, the CV of MUNIX gradually decreases with an increase in the number of channels, thereby optimizing the issue of abnormal MUNIX repeatability patterns and further enhancing the reproducibility of MUNIX based on high-density surface EMG signals.
As an essential joint, the function of the elbow joint is closely related to the body's activity and quality of life. A statistical study showed a significant prevalence of serious elbow injuries brought on by sports, falls and auto accidents [1]. Although there are more comprehensive treatments for elbow injuries, the complex biomechanical environment and anatomy of the elbow joint often lead to elbow stiffness after injury [2,3]. Sojbjerg [4] reported that the incidence of post-traumatic elbow stiffness was about 5%. In contrast, Dunham et al. [5] suggested that the rate was as high as 50%. The development of elbow stiffness can have more adverse effects on the patient's emotional state and daily work. Therefore, in order to provide targeted rehabilitation treatment, it is valuable to comprehend the mechanical characteristics and the soft tissue stress distribution around the elbow joint following stiffness.
The upper arm and forearm are connected by the elbow joint. It consists of the lower end of the humerus and the upper ends of the ulna and radius. The three joints (both the ulnar, brachioradial and superior radial-ulnar joints) are encased in the same joint capsule. The ligaments are closely related to the joint capsule [6,7]. After suffering a relatively minor injury, the structural and biochemical properties of the joint capsule are altered, resulting in thickening, reduced compliance and loss of mobility [7,8]. Capsule contracture contributes significantly to elbow stiffness, and the most basic pathological change is a fibrotic contracture of the joint capsule [9,10,11,12]. Morrey et al. [13] found that an elbow range of motion of 30° to 130° could accomplish 90% of the activities required for daily life. With the significant changes in modern life and work styles, the range of motion of the elbow necessary for modern life requires even larger amounts of motion [14,15]. Elbow stiffness is defined as the limitation of extension > 30° and flexion < 120° [5]. According to research, a 50% decrease in elbow range of motion can result in an 80% loss in upper extremity function [7,16]. Therefore, the aim of treatment is to restore the above range of motion.
For elbow stiffness due to capsular contracture, dynamic orthoses can be used as a measure to improve functional elbow motion and avoid reoperation [17]. Dynamic orthoses generate continuous traction on contracted tissues through specific mechanical structures. Plastic deformation of the soft tissue is achieved on the basis of the creep mechanism [18], increasing the range of motion of the joint [17,19]. However, the appropriate traction load for the elbow is unknown. Overstretching during treatment can cause soft tissue tears leading to greater soft tissue contractures [20]. Inadequate traction prevents the joint from being in maximum flexion and extension resulting in a contracture that can recur [17]. Therefore, it is necessary to determine the appropriate traction force. Current researchers use dynamic orthotics primarily on the basis of the principle that more force is needed to remodel the tissue [20]. A traction force of around 2N is used as a recommended value for the treatment of finger contractures [21], and it is clear that for the elbow a greater traction load is needed. Gluck et al. [22] used 40 N as the interaction force between the elbow and the orthosis to assess the biomechanical strength of the orthosis. Quantitative studies on the mechanical behavior of the interaction between the dynamic orthosis and the elbow joint during treatment are scarce [20,23,24]. Therefore, it is of practical interest to study the mechanical behavior of the elbow with a dynamic orthosis through biomechanical methods to select the appropriate traction force for the treatment of elbow contractures.
Finite element modeling is an important tool in the study of human biomechanical investigations. It is especially widely used to study hip and knee joints [25,26]. In addition, the emergence of new models has greatly enriched the field of biomechanical research [27,28,29,30,31,32]. Recently, several researchers have analyzed the biomechanics of the elbow joint with FE models. For example, Kamei et al. [33] constructed a FE model of the adult elbow to assess the effect of ulnar collateral ligament dysfunction on the stress and stress distribution in the humeral capitellum. Zarifian et al. [34] simulated different implants for the treatment of distal humerus fractures to determine the optimal implant configuration. Akkurt et al. [35] evaluated commonly used internal fixation of humeral shaft fractures with an FE model to provide further guidance to therapists. However, few studies have investigated FE models of joint capsular contracture, especially for traction treatment of the elbow joint.
In this study, we evaluated the effect of capsular contracture on the elbow joint using the FE approach to obtain appropriate traction. In addition, the mechanical behavior of traction in the treatment of elbow joint stiffness caused by joint capsular contracture was quantitatively evaluated. An FE model of the human elbow joint containing active muscle forces was created to simulate elbow joint traction with a dynamic orthosis. The results of the study provided a reference for the appropriate mechanical properties of different traction forces regarding joint capsular contracture.
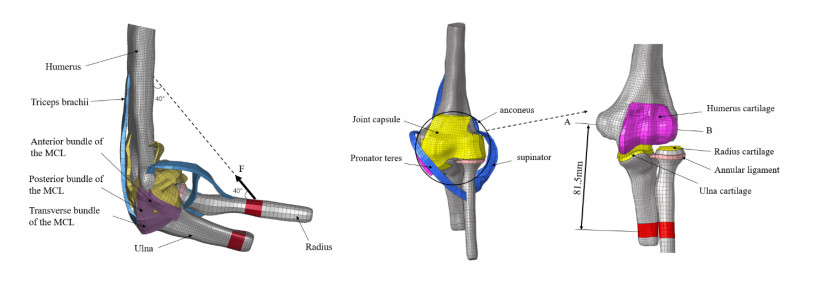
Computed tomography (CT) images (map tomography thickness, 1 mm; resolution, 256 × 256) were obtained for the elbow of a healthy 43-year-old male volunteer who signed a consent form. The CT images were imported into Mimics (Materialise Technologies, Leuven, Belgium) software, and the humerus, radius and ulna were extracted through a threshold segmentation method. Then, Geomagic software (Geomagic, Inc., NC, USA) was used to fill and smooth the bone models to obtain a high-quality 3D elbow joint bone model. Hypermesh (Altair Engineering Inc., USA) was used to create the soft tissue of the elbow joint in the appropriate anatomical position, as directed by an orthopedic surgeon. The process of mesh delineation, assignment of material properties, loading and application of boundary conditions were also completed in Hypermesh. Hexahedral mesh has the advantages of good deformation characteristics and high computational accuracy, and the number of elements and nodes required to achieve the same accuracy is much less than that of tetrahedral mesh [36]. Furthermore, hexahedral elements showed improved convergence. Therefore, an eight-node hexahedral finite element was used for meshing each part of the elbow joint. The complete finite element model is shown in Figure 1, including the ligaments (medial collateral ligament and lateral ulnar collateral ligament), bones, muscles and articular cartilage. A total of 32,725 nodes and 27,648 elements were included in the FE model. Table 1 shows that the material properties of each part of the model were derived from the data of several previous studies. Bone was analyzed biomechanically by treating it as an isotropic elastic material [37,38], which made the simulation results more accurate and closer to the real situation. Similarly, we defined ligaments, joint capsules, contractured capsule and articular cartilage as hyperelastic materials, following existing research [39,40,41].
| Model parameters | Parameter values | Parameter description |
| ρ (g·mm-3) | 1.06 × 10-3 | Density of the QLV model |
| v | 0.495 | Poisson's ratio of the QLV model |
| Ci | 0.991; 0; 34.65 | Instantaneous elastic response of the QLV model |
| Gi / MPa | 0.697; 1.086; 0.102; 0.1 | Viscous shear modulus of the QLV model |
| βi / s-1 | 589.1; 312.4; 1; 4.5 × 10-3 | Response to viscosity of the QLV model |
| бMax (MPa) | 0.5 | Maximum isometric contraction force |
| Lopt | 1.05 | Optimum length |
| Csh | 0.45 | Shape parameter of f(x) |
| VMax (m/s) | 0.945 | Maximum contraction velocity |
DownLoad:
CSV
Combining the passive nonlinear viscoelastic (QLV) element with the active Hill truss element allowed researchers to simulate both the active and passive dynamics of the muscle [42,43]. Integration of the nonlinear transient elastic response based on strain time produced the viscoelastic response of the QLV model. The instantaneous elastic response function, viscoelastic stress function, and viscoelastic stress relaxation function were defined by Eqs (1)–(3), respectively.
| σe=∑iciεi, | (1) |
| σ=∫t0G(t−τ)∂σe∂ε∂ε∂τdτ, | (2) |
| G(t)=∑nz=1G˙ie−βit. | (3) |
where Ci and σe are the instantaneous elastic response parameters and instantaneous elastic response, σ and Gi are the total stress and relaxation modulus and βi is the time constant. Equation (4) defined the active contraction force that the Hill model calculates.
| Fce=A(t)Fl(l)Fv(v)Fmax. | (4) |
where Fv(v) and Fmax are the muscle's velocity curve and maximal isometric contraction force, and A(t) and Fl(l) are the muscle's activation level curve and length curve, respectively [43,44,45]. The parameters of the QLV material proprioceptive model and Hill muscle proprioceptive model are recorded in Table 1.
Validation of the finite element model was completed by us. The validity of the model was demonstrated by applying forces ranging from 98 N to 490 N to the humeral interface, and the stress at the contact surface of the brachioradial joint was compared with the experimental findings of Takatori et al. [46]. The details of the validation procedure can be found in the literature [47].
Stretching with a dynamic orthosis within two weeks of elbow capsule injury may be counterproductive. Stretching traction caused additional differentiation of myofibroblasts, leading to further contracture of the joint capsule [2]. Dynamic orthoses may be appropriate three to four weeks after an elbow injury. At this time, collagen fibers are gradually forming and the orientation of the collagen fibers is determined by the direction of mechanical tension [48]. We chose to simulate a traction load intervention during the fourth week after the joint capsule injury. Early myofibroblasts were distributed in the anterior or posterior part of the joint capsule or both. In addition, clinical studies have suggested that myofibroblasts are an important cause of joint capsule contracture [2]. Therefore, three types of joint capsule contracture were considered in this paper: Total capsule contracture, anterior capsule contracture and posterior capsule contracture. The joint capsule was divided by us into anterior and posterior capsules according to the anatomical structure. The material parameters of the contractured capsule in Table 2 were assigned to the anterior capsule, posterior capsule and total capsule to realize the anterior capsular contracture model (ACC), posterior capsular contracture model (PCC) and total capsular contracture model (TCC). The healthy model was also assigned material parameters according to Table 2.
| Components | Elasticity's modulus (MPa) | Poisson's ratio |
| Bone | 15,000 | 0.3 |
| Articular cartilage | Neo-Hookean, C10 = 1.79 | |
| Healthy capsule | Neo-Hookean, C10 = 1.44 | |
| Ligaments | Neo-Hookean, C10 = 1.44 | |
| Contractured capsule | Neo-Hookean, C10 = 1.66 |
DownLoad:
CSV
In this model, the humerus was completely fixed, and the ulna and radius could be rotated only around the flexion axis. According to clinical statistics, the average restriction angle of the contractured elbow joint in flexion is 80 degrees [49]. Therefore, we used a flexion angle between 30 and 80 degrees. This work modeled elbow flexion under three conditions using an angular velocity of 1 rad/s [50,51]. TCC, ACC and PCC. Hackl et al. [52] fixed the elbow joint in flexion on a test stand. When the load was applied to the shaft end of the humerus, the forces through the ulnar-humeral and radial-humeral joints were approximately 25 and 75%, respectively. Therefore, at 80 degrees of elbow flexion, the traction forces were loaded on the ulna and radius at 25 and 75%, respectively, so that the FE model was closer to the actual force situation (Figure 1). The traction load sizes were 10, 20, 30 and 40 N. In addition, the distance between the position of the traction load application and the position of the axis of rotation of the elbow joint was approximately 81.5 mm, and the bending moments were approximately 0.524 N⋅m, 1.048 N⋅m, 1.572 N⋅m and 2.065 N⋅m [52].
Figure 2(a) shows how the ulnar cartilage (UC) was stressed during elbow flexion. The distribution of ulnar cartilage stress was very similar in TCC and PCC. In the initial phase of flexion, the ulnar cartilage stress was small, and the change was not apparent. As the flexion angle increased, the stress moved to the anterior medial side and reached its peak on the anterior medial side. At the end of flexion, the ulnar cartilage stress shifted toward the posterior medial side. Figure 2(b) demonstrates the ulnar cartilage stress distribution for the three contracture models under the four traction loads and shows significant changes in ulnar cartilage stress for each model after applying the traction loads. The stresses on the ulnar cartilage under traction were distributed on the edge and posterior medial side of the ulnar cartilage. During TCC, the ulnar cartilage stress distribution at 20 N was similar to that of the ulnar cartilage at 30 N, and during ACC, the ulnar cartilage stress distribution at 10 N was similar to that of the ulnar cartilage at 40 N. Figure 3 presents the changing traits of stress in the ligaments and cartilage under different stimuli. Compared with the healthy model, we observed a marked increase in stresses in all soft tissues except the anterior capsule and the transverse bundle of the MCL (tMCL) under different traction load conditions.
Stress trends in ulnar cartilage were similar for TCC and PCC (Figure 4(a)), with elevated ulnar cartilage stress between 30 and 50 degrees, and both were greater than ulnar cartilage stress in healthy model flexion. From 50 degrees to 60 degrees, the ulnar cartilage stress decreased and was less than the ulnar cartilage stress in healthy model flexion between 60 and 70 degrees. The peak stress of PCC at a flexion angle of 70 degrees was 1.06 MPa, which was around 1.05 times the maximum stress of healthy model flexion. The trend of the change in stress in ACC between 30 and 50 degrees of flexion was the opposite of that in the other cases, with the highest stress of 1.167 MPa observed at 70 degrees of flexion. The stress values of the anterior bundle of the MCL (aMCL) and the posterior bundle of the MCL (pMCL) increased with an increasing flexion angle, as shown in Figure 4(b), (c). For the aMCL, the stress trends were essentially the same for TCC and PCC from 30 degrees to 60 degrees. Overall, we observed the highest stress values in the TCC and PCC had from 30 degrees to 80 degrees of flexion and the lowest stress values in healthy model flexion. The maximum peak stress at 80 degrees of flexion was 4.06 MPa (PCC), which was around 1.05 times the maximum flexion stress in the healthy model. The stress values of the pMCL in different states were very similar, and the stress values of TCC from 40 degrees to 60 degrees were the smallest. For the tMCL, the stress values for ACC and healthy model flexion were essentially the same, and the stress values for TCC from 30 degrees to 50 degrees were higher than those in the other cases. The TCC and PCC stress values from 50 degrees to 80 degrees were lower than those in the other two cases. The stress values for TCC and PCC from 50 degrees to 80 degrees were lower than those in the other two cases, and the peak stress for PCC decreased by 34% from that in healthy model flexion (Figure 4(d)). The difference in stress variation in the lateral ulnar collateral ligament (LUCL) was more pronounced, with a maximum peak stress in TCC and PCC 1.78 times greater than that in healthy model flexion (Figure 4(e)). The stress values of the anterior capsule in different states are shown in Figure 4(f). The ACC had the lowest stress value, with a 49% reduction in maximum peak stress from that in healthy model flexion. The TCC had the largest stress value, with a maximum peak stress approximately 1.1 times higher than that in healthy model flexion. For the posterior capsule (Figure 4(g)), the ACC had the largest value of stress in the overall range of flexion, with a maximum peak stress approximately 1.3 times higher than that in the healthy model flexion stress value.
Dynamic orthoses are an effective means of treating elbow stiffness and restoring the functional arc of motion to the elbow [2]. The treatment process requires appropriate traction to achieve soft tissue plastic deformation and thus increase elbow mobility. Currently, improvement in elbow mobility in rehabilitation is mainly observed with macroscopic movements [19,24]. The internal biomechanics of the elbow joint is complex, and the study of stress in the soft tissue of the elbow under the state of capsular contracture is not completely clear. Furthermore, quantitative studies on the mechanical behavior of the interaction between the dynamic orthosis and the elbow joint are scarce. In this study, we developed a healthy model, TCC model, ACC model and PCC model. First, we assessed the stresses of different types of soft tissues in the elbow joint during flexion in comparison with the healthy model to provide constructive options for traction force treatment for elbow joint contracture. Then, we investigated the mechanical response of the elbow joint after applying the traction load to determine the appropriate traction load.
The results showed that the soft tissue stress values were very similar for TCC and PCC, and the ulnar cartilage stress distribution was also very similar. In the range of 50 to 60 degrees of flexion, the stress on the posterior medial aspect of the ulnar cartilage was transferred to the anterior medial aspect of the ulnar cartilage, where the notch of the ulnar trochlear was located. This was consistent with clinical autopsy results [53]. In addition, the distribution and transfer of ulnar cartilage stress in TCC and PCC during elbow flexion were comparable to those in healthy model flexion (Figure 2(a)). In the range of 30 degrees to 50 degrees, ulnar stresses in TCC and PCC were greater than those in the healthy model and increased with an increasing flexion angle (Figure 4(a)). The ulnar cartilage stress was reduced by 18% (at 50 degrees) in TCC compared with PCC. This suggests that ulnar cartilage stress was less affected by the anterior capsule. Therefore, we hypothesized that the posterior capsule plays a greater role in the flexion process than the anterior capsule after the contracture of the joint capsule. This was consistent with the findings of King et al. [54]. When the elbow was flexed from 30 to 80 degrees, more posterior capsule stress was observed in the ACC state than in other situations (Figure 4(g)). According to reports, the collagen fibers in the healthy anterior capsule were extremely dispersed and relatively thin and elastic [11]. We speculated that the reduced flexibility of the contracted anterior capsule created an obstacle in the process of elbow flexion, resulting in increased stress on the posterior capsule. This finding was consistent with the findings of Gallay et al. [55], who found that the compliance of the contracted elbow capsule was one-sixth that of the healthy elbow joint. We further hypothesized that for the ACC condition, traction should not be excessive to avoid straining the posterior capsule. We found that posterior capsular contracture and total capsular contracture had a greater effect on tMCL stress during 60 to 80 degrees of elbow flexion, whereas anterior capsular contracture had little effect on tMCL stress (Figure 4(d)). This suggests that there is some connection between the posterior capsule and the tMCL. The reason for this we can find an explanation in the anatomic structure of the elbow. Kimata et al. [56] found that the tMCL is strongly connected to the posterior capsule. tMCL contributes the least to the stability of the contracted elbow joint [57]. When the posterior capsule is contracted, the stress on the tMCL decreases and its contribution to elbow stability is further weakened. This was an additional finding of this study.
Higher traction forces can lead not only to soft tissue injuries but also to the instability of the elbow joint. Morrey et al. [58] reported that the articular surface of the superior ulna was the primary stabilizer of the elbow joint. Joint instability is indicated by changes in the ulnar cartilage stress distribution compared with a healthy model. Therefore, it was necessary to analyze the stability of the elbow joint by comparing the stress distribution of the ulnar cartilage under various traction forces. We compared the ulnar cartilage stress distribution in a contracture model loaded with traction (Figure 2(b)) and in a healthy model flexed to 80 degrees (Figure 2(a)). The stress distribution of the ulnar cartilage under 20 and 30 N traction loads during TCC (Figure 2(b)) was similar to that of the ulnar cartilage of the healthy model with a flexion angle of 80 degrees (Figure 2(a)). This phenomenon showed that the elbow joint with TCC was more stabilized by traction loads of 20 and 30 N than by traction loads of 10 and 40 N. By analyzing Table 3 and Figure 3(a), we found that in TCC, the stress values of each soft tissue at 20 N were closer to those in the healthy model than at 30 N. It was reported that low load traction helped the tissue slowly undergo plastic deformation [19]. Consequently, it was important to focus on the traction load that brought the stress values of each soft tissue of the contractured elbow joint close to the stress values of each soft tissue in the healthy model while maintaining the stability of the elbow joint. This showed that the elbow joint with TCC was more conducive to tissues slowly undergoing plastic deformation by traction loads of 20 N than by traction loads of 30 N. Thus, the appropriate traction force for the elbow joint with TCC was determined to be 20 N. Following the same approach, we found that the stress distribution of the ulnar cartilage under 10 N and 40 N traction loads during ACC (Figure 2(b)) was similar to that of the ulnar cartilage of the healthy model with a flexion angle of 80 degrees (Figure 2(a)). As stated in the previous paragraph, we concluded that the traction load should not be excessive in ACC. As shown in Table 4 and Figure 3(b), we found that in ACC, the stress values of each soft tissue at 10 N were more similar to those in the healthy model than at 40 N. Consequently, the appropriate traction force for the elbow joint with ACC was determined to be 10 N. The stress distribution of the ulnar cartilage under 10 and 20 N traction loads during PCC (Figure 2(b)) was similar to that of the ulnar cartilage of the healthy model with a flexion angle of 80 degrees (Figure 2(a)). As shown in Table 5 and Figure 3(c), we found that in PCC, the stress values of each soft tissue at 20 N were more similar to those in the healthy model than at 10 N. Therefore, we determined that the appropriate traction force for the elbow joint with PCC was 20 N. The results showed that most of the soft tissue stress values increased under all four traction loads, indicating that the traction loads exerted pull on the soft tissues, which is consistent with the creep mechanism of the dynamic orthosis in the actual treatment process [19]. Unsuitable traction can lead to soft tissue tears [20], which can be painful. We also found that unsuitable traction can lead to changes in the stress distribution in the ulnar cartilage, which may be responsible for the patient's discomfort.
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.543 | 1.26 | 1.54 | 2.61 |
| aMCL | 3.46 | 4.13 | 3.94 | 3.93 | 3.95 |
| pMCL | 8.11 | 8.22 | 8.21 | 8.4 | 8.52 |
| tMCL | 0.405 | 0.285 | 0.27 | 0.306 | 0.305 |
| LUCL | 2.26 | 4.18 | 4.08 | 4.06 | 4.08 |
| Capsule | 11.5 | 12 | 12.1 | 12.5 | 12.6 |
DownLoad:
CSV
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.691 | 0.951 | 2.26 | 2.58 |
| aMCL | 3.46 | 3.59 | 3.68 | 3.51 | 3.54 |
| pMCL | 8.11 | 8.28 | 8.5 | 8.65 | 8.75 |
| tMCL | 0.405 | 0.429 | 0.421 | 0.471 | 0.474 |
| LUCL | 2.26 | 3.02 | 3.05 | 3.09 | 3.1 |
| PC | 11.5 | 13.9 | 14 | 15 | 12.5 |
| AC | 11.5 | 5.46 | 5.41 | 5.53 | 6.22 |
DownLoad:
CSV
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.533 | 0.55 | 1.94 | 2.44 |
| aMCL | 3.46 | 4.04 | 4.17 | 3.99 | 3.73 |
| pMCL | 8.11 | 8.36 | 8.18 | 8.4 | 8.68 |
| tMCL | 0.405 | 0.267 | 0.27 | 0.293 | 0.296 |
| LUCL | 2.26 | 3.85 | 3.97 | 3.95 | 4.15 |
| PC | 11.5 | 12.3 | 12.2 | 12.4 | 12.6 |
| AC | 11.5 | 9.12 | 9.28 | 8.84 | 9.06 |
DownLoad:
CSV
Although many studies have investigated the treatment of elbow contractures with braces, few studies have assessed the selection of appropriate traction for the treatment of elbow contractures. At this stage, researchers have mainly applied traction forces based on the principle that more force is needed to remodel the tissue [20]. In addition, many studies have been conducted to evaluate the clinical efficacy of dynamic orthoses for the treatment of elbow contractures [59,60,61] and focused on the mechanical design of dynamic orthoses [62,63,64,65]. The traction in our study can be used as a reference for clinical treatment to achieve satisfactory therapeutic results. The method can also be combined with a clinical approach to customize rehabilitation programs for specific patients based on the different contracture locations of the elbow joint.
This study was limited by the simplification of the FE model. Because of this, the model could not respond to the elbow biomechanical environment with high accuracy. In addition, the model developed in this work simulated the state of traction load intervention during the fourth week of joint capsule injury. However, traction bracing for elbow stiffness is a long-term process [23]. In this study, we did not account for the long-term behavior of the traction support with the elbow. As the soft tissues of the elbow undergo plastic deformation by traction, the material properties and internal structure of the soft tissues are altered [19]. Therefore, in a future study, we will consider this biological process by studying soft tissue material properties in animal models.
We constructed a finite element model of the elbow to simulate the flexion process of the contracted elbow and investigated the mechanical response of the elbow joint after applying the traction load. We observed a significant increase in posterior capsule stress with anterior capsular contracture, and the maximum peak stress was 1.3 times higher than that in the healthy model. The traction load was shown to have a significant effect on the biomechanical response of the elbow joint. The appropriate traction forces for total, anterior and posterior capsular contractures were 20, 10 and 20 N, respectively, in the fourth week after elbow capsule injury, which could maintain a stable biomechanical environment for the elbow joint and achieve a soft tissue pulling effect, thereby increasing elbow mobility. The results could provide quantitative guidance to the rehabilitation physician in determining the traction load for a specific patient.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
This study was supported by funds from National Natural Science Foundation of China (NSFC) Research Grants (12102301; 31871212; 51975411).
The authors declare that there are no conflicts of interest.
| [1] |
A. A. Lari, A. A. Ghavanini, H. R. Bokaee, A review of electrophysiological studies of lower motor neuron involvement in amyotrophic lateral sclerosis, Neurol. Sci., 40 (2019), 1125–1136. https://doi.org/10.1007/s10072-019-03832-4 doi: 10.1007/s10072-019-03832-4
|
| [2] |
J. Nijssen, L. H. Comley, E. Hedlund, Motor neuron vulnerability and resistance in amyotrophic lateral sclerosis, Acta Neuropathol., 133 (2017), 863–885. https://doi.org/10.1007/s00401-017-1708-8 doi: 10.1007/s00401-017-1708-8
|
| [3] |
S. D. Nandedkar, D. S. Nandedkar, P. E. Barkhaus, E. V. Stalberg, Motor unit number index (MUNIX), IEEE Trans. Biomed. Eng., 51 (2004), 2209–2211. https://doi.org/10.1109/TBME.2004.834281 doi: 10.1109/TBME.2004.834281
|
| [4] |
S. D. Nandedkar, P. E. Barkhaus, E. V. StÅlberg, Motor unit number index (MUNIX): principle, method, and findings in healthy subjects and in patients with motor neuron disease, Muscle Nerve, 42 (2010), 798–807. https://doi.org/10.1002/mus.21824 doi: 10.1002/mus.21824
|
| [5] |
Q. Xu, S. Xue, F. Gao, Q. Wu, Q. Zhang, Evaluation method of motor unit number index based on optimal muscle strength combination, Math. Biosci. Eng., 20 (2023), 3854–3872. https://doi.org/10.3934/mbe.2023181 doi: 10.3934/mbe.2023181
|
| [6] |
W. A. Boekestein, H. J. Schelhaas, M. J. A. M. van Putten, D. F. Stegeman, M. J. Zwarts, J. P. van Dijk, Motor unit number index (MUNIX) versus motor unit number estimation (MUNE): a direct comparison in a longitudinal study of ALS patients, Clin. Neurophysiol., 123 (2012), 1644–1649. https://doi.org/10.1016/j.clinph.2012.01.004 doi: 10.1016/j.clinph.2012.01.004
|
| [7] |
C. Neuwirth, P. E. Barkhaus, C. Burkhardt, J. Castro, D. Czell, M. de Carvalho, et al., Tracking motor neuron loss in a set of six muscles in amyotrophic lateral sclerosis using the motor unit number index (MUNIX): a 15-month longitudinal multicentre trial, J. Neurol. Neurosurg. Psychiatry, 86 (2015), 1172–1179. https://doi.org/10.1136/jnnp-2015-310509 doi: 10.1136/jnnp-2015-310509
|
| [8] |
J. Furtula, B. Johnsen, P. B. Christensen, K. Pugdahl, C. Bisgaard, M. K. Christensen, et al., MUNIX and incremental stimulation MUNE in ALS patients and control subjects, Clin. Neurophysiol., 124 (2013), 610–618. https://doi.org/10.1016/j.clinph.2012.08.023 doi: 10.1016/j.clinph.2012.08.023
|
| [9] |
S. D. Nandedkar, P. E. Barkhaus, E. V. Stålberg, Reproducibility of MUNIX in patients with amyotrophic lateral sclerosis, Muscle Nerve, 44 (2011), 919–922. https://doi.org/10.1002/mus.22204 doi: 10.1002/mus.22204
|
| [10] |
C. Neuwirth, S. Nandedkar, E. Stålberg, P. E. Barkhaus, M. de Carvalho, J. Furtula, et al., Motor unit number index (MUNIX): a novel neurophysiological marker for neuromuscular disorders; test-retest reliability in healthy volunteers, Clin. Neurophysiol., 122 (2011), 1867–1872. https://doi.org/10.1016/j.clinph.2011.02.017 doi: 10.1016/j.clinph.2011.02.017
|
| [11] |
N. Dias, X. Li, C. Zhang, Y. Zhang, Innervation asymmetry of the external anal sphincter in aging characterized from high-density intra-rectal surface EMG recordings, Neurourol. Urodyn., 37 (2018), 2544–2550. https://doi.org/10.1002/nau.23809 doi: 10.1002/nau.23809
|
| [12] |
R. Günther, C. Neuwirth, J. C. Koch, P. Lingor, N. Braun, R. Untucht, et al., Motor unit number index (MUNIX) of hand muscles is a disease biomarker for adult spinal muscular atrophy, Clin. Neurophysiol., 130 (2019), 315–319. https://doi.org/10.1016/j.clinph.2018.11.009 doi: 10.1016/j.clinph.2018.11.009
|
| [13] |
C. Neuwirth, C. Burkhardt, J. Alix, J. Castro, M. de Carvalho, M. Gawel, et al., Quality control of motor unit number index (MUNIX) measurements in 6 muscles in a single-subject "round-robin" setup, PLoS One, 11 (2016), e0153948. https://doi.org/10.1371/journal.pone.0153948 doi: 10.1371/journal.pone.0153948
|
| [14] |
S. W. Ahn, S. H. Kim, J. E. Kim, S. M. Kim, S. H. Kim, K. S. Park, et al., Reproducibility of the motor unit number index (MUNIX) in normal controls and amyotrophic lateral sclerosis patients, Muscle Nerve, 42 (2010), 808–813. https://doi.org/10.1002/mus.21765 doi: 10.1002/mus.21765
|
| [15] |
C. Neuwirth, N. Braun, K. G. Claeys, R. Bucelli, C. Fournier, M. Bromberg, et al., Implementing motor unit number index (MUNIX) in a large clinical trial: Real world experience from 27 centres, Clin. Neurophysiol., 129 (2018), 1756–1762. https://doi.org/10.1016/j.clinph.2018.04.614 doi: 10.1016/j.clinph.2018.04.614
|
| [16] |
D. Fathi, B. Mohammadi, R. Dengler, S. Böselt, S. Petri, K. Kollewe, Lower motor neuron involvement in ALS assessed by motor unit number index (MUNIX): long-term changes and reproducibility, Clin. Neurophysiol., 127 (2016), 1984–1988. https://doi.org/10.1016/j.clinph.2015.12.023 doi: 10.1016/j.clinph.2015.12.023
|
| [17] |
C. Neuwirth, S. Nandedkar, E. StåLberg, M. Weber, Motor unit number index (MUNIX): a novel neurophysiological technique to follow disease progression in amyotrophic lateral sclerosis, Muscle Nerve, 42 (2010), 379–384. https://doi.org/10.1002/mus.21707 doi: 10.1002/mus.21707
|
| [18] |
F. Fatehi, E. Delmont, A. M. Grapperon, E. Salort-Campana, A. Sévy, A. Verschueren, et al., Motor unit number index (MUNIX) in patients with anti-MAG neuropathy, Clin. Neurophysiol., 128 (2017), 1264–1269. https://doi.org/10.1016/j.clinph.2017.04.022 doi: 10.1016/j.clinph.2017.04.022
|
| [19] |
F. Fatehi, A. M. Grapperon, D. Fathi, E. Delmont, S. Attarian, The utility of motor unit number index: a systematic review, Neurophysiol. Clin., 48 (2018), 251–259. https://doi.org/10.1016/j.neucli.2018.09.001 doi: 10.1016/j.neucli.2018.09.001
|
| [20] |
E. Issoglio, P. Smith, J. Voss, On the estimation of entropy in the FastICA algorithm, J. Multivar. Anal., 181 (2021), 104689. https://doi.org/10.1016/j.jmva.2020.104689 doi: 10.1016/j.jmva.2020.104689
|
| [21] |
F. Gao, Y. Cao, C. Zhang, Y. Zhang, A preliminary study of effects of channel number and location on the repeatability of motor unit number index (MUNIX), Front. Neurol., 11 (2020), 191. https://doi.org/10.3389/fneur.2020.00191 doi: 10.3389/fneur.2020.00191
|
| [22] |
Y. Peng, J. He, B. Yao, S. Li, P. Zhou, Y. Zhang, Motor unit number estimation based on high-density surface electromyography decomposition, Clin. Neurophysiol., 127 (2016), 3059–3065. https://doi.org/10.1016/j.clinph.2016.06.014 doi: 10.1016/j.clinph.2016.06.014
|
| [23] |
B. Cao, X. Gu, L. Zhang, Y. Hou, Y. Chen, Q. Wei, et al., Reference values for the motor unit number index and the motor unit size index in five muscles, Muscle Nerve, 61 (2020), 657–661. https://doi.org/10.1002/mus.26837 doi: 10.1002/mus.26837
|
| [24] | Q. Li, J. Yang, Research on the surface electromyography signal decomposition based on multi-channel signal fusion analysis, J. Biomed. Eng., 29 (2012), 948–953. |
| [25] |
A. Hyvarinen, Fast and robust fixed-point algorithms for independent component analysis, IEEE Trans. Neural Networks, 10 (1999), 626–634. https://doi.org/10.1109/72.761722 doi: 10.1109/72.761722
|
| [26] |
Z. Liu, D. Yang, Y. Wang, M. Lu, R. Li, EGNN: Graph structure learning based on evolutionary computation helps more in graph neural networks, Appl. Soft Comput., 135 (2023), 110040. https://doi.org/10.1016/j.asoc.2023.110040 doi: 10.1016/j.asoc.2023.110040
|
| [27] |
M. L. Escorcio-Bezerra, A. Abrahao, D. Santos-Neto, N. I. de Oliveira Braga, A. S. B. Oliveira, G. M. Manzano, et al., Why averaging multiple MUNIX measures in the longitudinal assessment of patients with ALS? Clin. Neurophysiol., 128 (2017), 2392–2396. https://doi.org/10.1016/j.clinph.2017.09.104 doi: 10.1016/j.clinph.2017.09.104
|
| [28] |
C. Dai, X. Hu, Independent component analysis based algorithms for high-density electromyogram decomposition: experimental evaluation of upper extremity muscles, Comput. Biol. Med., 108 (2019), 42–48. https://doi.org/10.1016/j.compbiomed.2019.03.009 doi: 10.1016/j.compbiomed.2019.03.009
|
| [29] |
J. Thomas, Y. Deville, S. Hosseini, Differential fast fixed-point algorithms for underdetermined instantaneous and convolutive partial blind source separation, IEEE Trans. Signal Process., 55 (2007), 3717–3729. https://doi.org/10.1109/TSP.2007.894243 doi: 10.1109/TSP.2007.894243
|
| [30] |
M. Chen, X. Zhang, Z. Lu, X. Li, P. Zhou, Two-source validation of progressive FastICA peel-off for automatic surface EMG decomposition in human first dorsal interosseous muscle, Int. J. Neural Syst., 28 (2018), 1850019. https://doi.org/10.1142/S0129065718500193 doi: 10.1142/S0129065718500193
|
| [31] |
M. Chen, X. Zhang, P. Zhou, A novel validation approach for high density surface EMG decomposition in motor neuron disease, IEEE Trans. Neural Syst. Rehabil. Eng., 26 (2018), 1161–1168. https://doi.org/10.1109/TNSRE.2018.2836859 doi: 10.1109/TNSRE.2018.2836859
|
| [32] |
M. Liu, J. Yang, E. Fan, J. Qiu, W. Zheng, Leak location procedure based on the complex-valued FastICA blind deconvolution algorithm for water-filled branch pipe, Water Supply, 22 (2022), 2560–2572. https://doi.org/10.2166/ws.2021.450 doi: 10.2166/ws.2021.450
|
| [33] |
M. Chen, P. Zhou, Automatic decomposition of pediatric high density surface EMG: a pilot study, Med. Novel Technol. Devices, 12 (2021), 100094. https://doi.org/10.1016/j.medntd.2021.100094 doi: 10.1016/j.medntd.2021.100094
|
| [34] |
M. Drey, C. Grösch, C. Neuwirth, J. M. Bauer, C. C. Sieber, The motor unit number index (MUNIX) in sarcopenic patients, Exp. Gerontol., 48 (2013), 381–384. https://doi.org/10.1016/j.exger.2013.01.011 doi: 10.1016/j.exger.2013.01.011
|
| [35] |
W. Qi, S. E. Ovur, Z. Li, A. Marzullo, R. Song, Multi-sensor guided and gesture recognition for a teleoperated robot using a recurrent neural network, IEEE Rob. Autom. Lett., 6 (2021), 6039–6045. https://doi.org/10.1109/LRA.2021.3089999 doi: 10.1109/LRA.2021.3089999
|
| [36] |
W. Qi, H. Su, A cybertwin based multimodal network for ECG patterns monitoring using deep learning, IEEE Trans. Ind. Inf., 18 (2022), 6663–6670. https://doi.org/10.1109/TⅡ.2022.3159583 doi: 10.1109/TⅡ.2022.3159583
|
| [37] |
C. Tian, Z. Xu, L. Wang, Y. Liu, Arc fault detection using artificial intelligence: challenges and benefits, Math. Biosci. Eng., 20 (2023), 12404–12432. https://doi.org/10.3934/mbe.2023552 doi: 10.3934/mbe.2023552
|
| [38] |
Y. Shi, L. Li, J. Yang, Y. Wang, S. Hao, Center-based transfer feature learning with classifier adaptation for surface defect recognition, Mech. Syst. Signal Process., 188 (2023), 110001. https://doi.org/10.1016/j.ymssp.2022.110001 doi: 10.1016/j.ymssp.2022.110001
|
| [39] |
Y. Wang, Z. Liu, J. Xu, W. Yan, Heterogeneous network representation learning approach for ethereum identity identification, IEEE Trans. Comput. Social Syst., 10 (2023), 890–899. https://doi.org/10.1109/TCSS.2022.3164719 doi: 10.1109/TCSS.2022.3164719
|
| [40] |
M. Gawel, M. Kuzma-Kozakiewicz, Does the MUNIX method reflect clinical dysfunction in amyotrophic lateral sclerosis: a practical experience, Medicine, 95 (2016), e3647. https://doi.org/10.1097/MD.0000000000003647 doi: 10.1097/MD.0000000000003647
|
| [41] |
S. Li, J. Liu, M. Bhadane, P. Zhou, W. Z. Rymer, Activation deficit correlates with weakness in chronic stroke: evidence from evoked and voluntary EMG recordings, Clin. Neurophysiol., 125 (2014), 2413–2417. https://doi.org/10.1016/j.clinph.2014.03.019 doi: 10.1016/j.clinph.2014.03.019
|
| [42] |
Y. Peng, Y. C. Zhang, Improving the repeatability of motor unit number index (MUNIX) by introducing additional epochs at low contraction levels, Clin. Neurophysiol., 128 (2017), 1158–1165. https://doi.org/10.1016/j.clinph.2017.03.044 doi: 10.1016/j.clinph.2017.03.044
|
| [43] |
C. W. Chin, A short and elementary proof of the central limit theorem by individual swapping, Am. Math. Mon., 129 (2022), 374–380. https://doi.org/10.1080/00029890.2022.2027711 doi: 10.1080/00029890.2022.2027711
|
| [44] |
J. Miettinen, K. Nordhausen, H. Oja, S. Taskinen, Deflation-based FastICA with adaptive choices of nonlinearities, IEEE Trans. Signal Process., 62 (2014), 5716–5724. https://doi.org/10.1109/TSP.2014.2356442 doi: 10.1109/TSP.2014.2356442
|
| [45] |
J. P. van Dijk, J. H. Blok, B. G. Lapatki, I. N. van Schaik, M. J. Zwarts, D. F. Stegeman, Motor unit number estimation using high-density surface electromyography, Clin. Neurophysiol., 119 (2008), 33–42. https://doi.org/10.1016/j.clinph.2007.09.133 doi: 10.1016/j.clinph.2007.09.133
|
| [46] |
X. Li, Y. C. Wang, N. L. Suresh, W. Z. Rymer, P. Zhou, Motor unit number reductions in paretic muscles of stroke survivors, IEEE Trans. Inf. Technol. Biomed., 15 (2011), 505–512. https://doi.org/10.1109/TITB.2011.2140379 doi: 10.1109/TITB.2011.2140379
|
Figures(9) / Tables(3)
Suqi Xue, Farong Gao, Xudong Wu, Qun Xu, Xuecheng Weng, Qizhong Zhang. MUNIX repeatability evaluation method based on FastICA demixing[J]. Mathematical Biosciences and Engineering, 2023, 20(9): 16362-16382. doi: 10.3934/mbe.2023730
| Model parameters | Parameter values | Parameter description |
| ρ (g·mm-3) | 1.06 × 10-3 | Density of the QLV model |
| v | 0.495 | Poisson's ratio of the QLV model |
| Ci | 0.991; 0; 34.65 | Instantaneous elastic response of the QLV model |
| Gi / MPa | 0.697; 1.086; 0.102; 0.1 | Viscous shear modulus of the QLV model |
| βi / s-1 | 589.1; 312.4; 1; 4.5 × 10-3 | Response to viscosity of the QLV model |
| бMax (MPa) | 0.5 | Maximum isometric contraction force |
| Lopt | 1.05 | Optimum length |
| Csh | 0.45 | Shape parameter of f(x) |
| VMax (m/s) | 0.945 | Maximum contraction velocity |
DownLoad:
CSV
| Components | Elasticity's modulus (MPa) | Poisson's ratio |
| Bone | 15,000 | 0.3 |
| Articular cartilage | Neo-Hookean, C10 = 1.79 | |
| Healthy capsule | Neo-Hookean, C10 = 1.44 | |
| Ligaments | Neo-Hookean, C10 = 1.44 | |
| Contractured capsule | Neo-Hookean, C10 = 1.66 |
DownLoad:
CSV
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.543 | 1.26 | 1.54 | 2.61 |
| aMCL | 3.46 | 4.13 | 3.94 | 3.93 | 3.95 |
| pMCL | 8.11 | 8.22 | 8.21 | 8.4 | 8.52 |
| tMCL | 0.405 | 0.285 | 0.27 | 0.306 | 0.305 |
| LUCL | 2.26 | 4.18 | 4.08 | 4.06 | 4.08 |
| Capsule | 11.5 | 12 | 12.1 | 12.5 | 12.6 |
DownLoad:
CSV
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.691 | 0.951 | 2.26 | 2.58 |
| aMCL | 3.46 | 3.59 | 3.68 | 3.51 | 3.54 |
| pMCL | 8.11 | 8.28 | 8.5 | 8.65 | 8.75 |
| tMCL | 0.405 | 0.429 | 0.421 | 0.471 | 0.474 |
| LUCL | 2.26 | 3.02 | 3.05 | 3.09 | 3.1 |
| PC | 11.5 | 13.9 | 14 | 15 | 12.5 |
| AC | 11.5 | 5.46 | 5.41 | 5.53 | 6.22 |
DownLoad:
CSV
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.533 | 0.55 | 1.94 | 2.44 |
| aMCL | 3.46 | 4.04 | 4.17 | 3.99 | 3.73 |
| pMCL | 8.11 | 8.36 | 8.18 | 8.4 | 8.68 |
| tMCL | 0.405 | 0.267 | 0.27 | 0.293 | 0.296 |
| LUCL | 2.26 | 3.85 | 3.97 | 3.95 | 4.15 |
| PC | 11.5 | 12.3 | 12.2 | 12.4 | 12.6 |
| AC | 11.5 | 9.12 | 9.28 | 8.84 | 9.06 |
DownLoad:
CSV
| Model parameters | Parameter values | Parameter description |
| ρ (g·mm-3) | 1.06 × 10-3 | Density of the QLV model |
| v | 0.495 | Poisson's ratio of the QLV model |
| Ci | 0.991; 0; 34.65 | Instantaneous elastic response of the QLV model |
| Gi / MPa | 0.697; 1.086; 0.102; 0.1 | Viscous shear modulus of the QLV model |
| βi / s-1 | 589.1; 312.4; 1; 4.5 × 10-3 | Response to viscosity of the QLV model |
| бMax (MPa) | 0.5 | Maximum isometric contraction force |
| Lopt | 1.05 | Optimum length |
| Csh | 0.45 | Shape parameter of f(x) |
| VMax (m/s) | 0.945 | Maximum contraction velocity |
| Components | Elasticity's modulus (MPa) | Poisson's ratio |
| Bone | 15,000 | 0.3 |
| Articular cartilage | Neo-Hookean, C10 = 1.79 | |
| Healthy capsule | Neo-Hookean, C10 = 1.44 | |
| Ligaments | Neo-Hookean, C10 = 1.44 | |
| Contractured capsule | Neo-Hookean, C10 = 1.66 |
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.543 | 1.26 | 1.54 | 2.61 |
| aMCL | 3.46 | 4.13 | 3.94 | 3.93 | 3.95 |
| pMCL | 8.11 | 8.22 | 8.21 | 8.4 | 8.52 |
| tMCL | 0.405 | 0.285 | 0.27 | 0.306 | 0.305 |
| LUCL | 2.26 | 4.18 | 4.08 | 4.06 | 4.08 |
| Capsule | 11.5 | 12 | 12.1 | 12.5 | 12.6 |
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.691 | 0.951 | 2.26 | 2.58 |
| aMCL | 3.46 | 3.59 | 3.68 | 3.51 | 3.54 |
| pMCL | 8.11 | 8.28 | 8.5 | 8.65 | 8.75 |
| tMCL | 0.405 | 0.429 | 0.421 | 0.471 | 0.474 |
| LUCL | 2.26 | 3.02 | 3.05 | 3.09 | 3.1 |
| PC | 11.5 | 13.9 | 14 | 15 | 12.5 |
| AC | 11.5 | 5.46 | 5.41 | 5.53 | 6.22 |
| soft tissue | Healthy model (MPa) | 10 N (MPa) | 20 N (MPa) | 30 N (MPa) | 40 N (MPa) |
| UC | 0.573 | 0.533 | 0.55 | 1.94 | 2.44 |
| aMCL | 3.46 | 4.04 | 4.17 | 3.99 | 3.73 |
| pMCL | 8.11 | 8.36 | 8.18 | 8.4 | 8.68 |
| tMCL | 0.405 | 0.267 | 0.27 | 0.293 | 0.296 |
| LUCL | 2.26 | 3.85 | 3.97 | 3.95 | 4.15 |
| PC | 11.5 | 12.3 | 12.2 | 12.4 | 12.6 |
| AC | 11.5 | 9.12 | 9.28 | 8.84 | 9.06 |
