A comparative study of pull-out performance of bolted joints in pultruded FRP with drilled holes or punched holes

1.   Introduction

The pultrusion process is an industrial production process for preparing the uniform-section linear composite products. Compared with other composite molding processes, it boasts such advantages as high production efficiency and stable product quality ^[1]. Composite profiles prepared by the pultrusion process enjoy advantages such as light weight, high strength and corrosion resistance as compared against traditional structural materials such as steel and concrete. Pultruded fiber reinforced polymer (PFRP) structures have been increasingly applied in the field of structural engineering, such as composite truss bridges, bridge decks, canopies, photovoltaic support brackets, railings, cooling towers, power towers, and so on ^[2,3,4].

The joint connection of composite profiles is a critical issue in engineering. Commonly-used connection forms include bolted joints, adhesive joints and hybrid (bonded/bolted) connection ^[5]. Among them, the adhesive joints have a small bearing capacity. Therefore, in projects where large loading capacity is required, the bolted joints or the hybrid connection is usually used. However, as the composite profile belongs to a typical orthotropic anisotropic material ^[6], it has a high longitudinal strength and modulus, yet a low lateral and shear strength and modulus, resulting in more complicated distribution of stress around the bolt hole ^[7], and thereby augmenting the difficulty of the bolted connection of composite profiles. Bearing this problem in mind, numerous scholars have made meaningful attempts, such as Rosner ^[8], Turvey ^[9], Erik ^[10] and Cooper and Turvey ^[11], and positive outcomes have been obtained. In their studies, all bolt holes were produced using the drilling method. Based on the valuable findings reported by the scholars, to ensure the safety of connection joints in composite profiles in engineering, the design specifications of composite profiles in various countries require that the bolt holes of composites shall be drilled ^[12,13,14]. For instance, according to American Composites Manufacturers Association, the holes in PFRP structures must be drilled or reamed ^[15]. However, drilling may not fully meet the requirements of the engineering. On the one hand, the manual drilling is low in efficiency. When the number of components and the number of bolted holes required in the engineering are numerous, it takes more time for manual drilling. On the other hand, drilling can only form round holes, and cannot form in-line and other non-round holes, which are widely used in the actual engineering. Therefore, it is imperative to adopt new hole forming methods to bore the composite profiles so as to meet the requirements of engineering.

Due to the continuous improvement in the pultrusion process, the application of high-performance resin and the breakthrough in the pultrusion process of multi-axial FRP, the lateral mechanical performance and shear performance of composite profiles are significantly improved, which further brings new potentials for the hole forming methods of FRP.

In this study, we propose a punching hole-making process for PFRP structures and investigate its feasibility in application. To the best of our knowledge, this approach has not been reported before. Using two types of PFRP composite profiles with high-performance resin and pultrusion process of multi-axial FRP as the experimental materials, we make various patterns of holes. Then, we carry out a pull-out experiment to study the mechanical performance and failure modes of the punched holes and bolted joints. Finally, using finite element software ABAQUS, we establish a more sophisticated model, combined with the progressive damage analysis (PDA) method, to simulate the pull-out process of the bolted joints in specimens with drilled holes or punched holes, respectively, and predict their failure behavior.

2.   Materials and method

2.1.   Experimental specimens

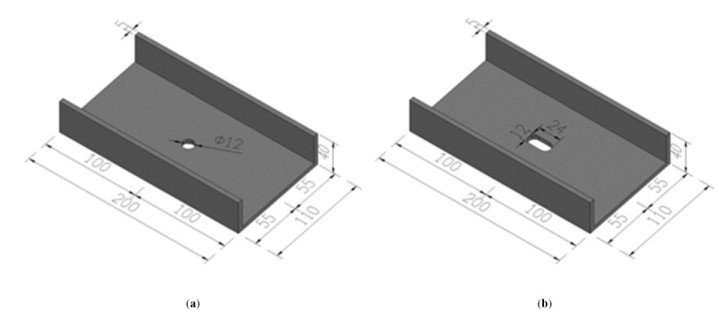
To investigate the impact of different resins and fiber directions on the pull-out performance of bolted joints, three types of pultruded FRP specimens are used in this experiment, namely, uni-axial unsaturated resin-based FRP, uni-axial polyurethane-based FRP and multi-axial unsaturated resin-based FRP. For each type, three parallels are made. All specimens together with some more details have been listed in Table 1, in which PU represents polyurethane resin, UP unsaturated polyester resin, S uni-axial fiber, M multi-axial fiber, D drilled holes, and P punched holes. The main material parameters of the specimens are shown in Table 2. The specimens are 200 ± 2.0 mm in length. The web width is 110 ± 1.1 mm, and the flange is 40 ± 0.5 mm in width. The thickness of both the web and flange is 5 ± 0.3 mm. The dimensions are detailed in Figure 1. The bolt hole diameter of the drilled specimens is 12 ± 0.2 mm. The long axis and short axis of the bolt hole of the punched specimens is 24 ± 0.2 mm and 6 ± 0.2 mm, respectively. The bolts used in the experiment are M10 steel bolts, provided with matching nuts as well as washers. The outer diameter and thickness of the washers are 25 ± 0.2 mm and 1 ± 0.2 mm, respectively.

Table 1.  Matrix, fiber directions (the angles are relative to the pultrusion direction) and fiber volume fractions of specimens (n = 3).

Specimens	Matrix	Fiber directions	Vf (%)
UPSD, UPSP	Unsaturated polyester resin	0°	64-68
PUSD, PUSP	Polyurethane resin	0°	76-82
UPMD, UPMP	Unsaturated polyester resin	0°:90°:±45°(6:4:3)	62-65

---

 | Show Table

DownLoad: CSV

Table 2.  Material properties of specimens.

Specimens	UPSD, UPSP	PUSD, PUSP	UPMD, UPMP
Longitudinal modulus, E1 (GPa)	20.45 ± 1.82	24.40 ± 2.23	18.20 ± 1.69
Transverse modulus, E2 (GPa)	8.80 ± 0.92	11.20 ±0.98	5.10 ± 0.46
In-plane shear modulus, G12 (GPa)	4.90 ± 0.45	6.10 ± 0.54	2.35 ± 0.21
Longitudinal tensile strength, XT (MPa)	2550 ± 196	3020 ±26	2360 ± 192
Transverse tensile strength, YT (MPa)	180 ± 14	340 ± 27	170 ± 15
Longitudinal compression strength, XC (MPa)	1560 ± 153	1747 ± 145	1340 ± 132
Transverse compression strength, YC (MPa)	250 ± 25	460 ± 37	230 ± 21
In plane shear strength, S12 (MPa)	96 ± 7	158 ± 13	140 ± 10
Out-of-plane shear strength, S23 (MPa)	50 ± 5	78 ± 7	19 ± 2

---

 | Show Table

DownLoad: CSV

Figure 1.  Size of specimens: (a) specimen withdrilled hole; (b) specimen with punched hole.

DownLoad: Full-Size Img PowerPoint

2.2.   Loading and measurement scheme

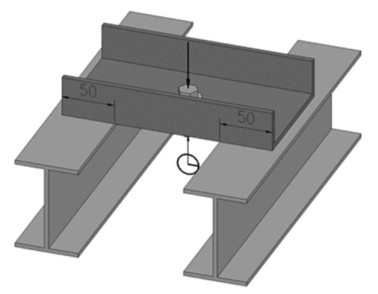
The loading device of the experiment is shown in Figure 2. The specimen is placed on the supports on both sides. The net span of the specimen is 100 ± 5 mm. The screw and washer are adjusted to the central position of the oblong hole. The bolt is screwed to the "tightening status" by means of the hand. Then load is added on the bolt head.

Figure 2.  Test set-up.

DownLoad: Full-Size Img PowerPoint

The loading is conducted by using the computer-controlled universal testing machine MTS5205, and controlled by means of displacement, with a loading rate of 1 mm/min.

A displacement meter is arranged on the lower end surface of the screw to measure the vertical displacement of the bolt under the action of load.

3.   Results

3.1.   Load-displacement curves

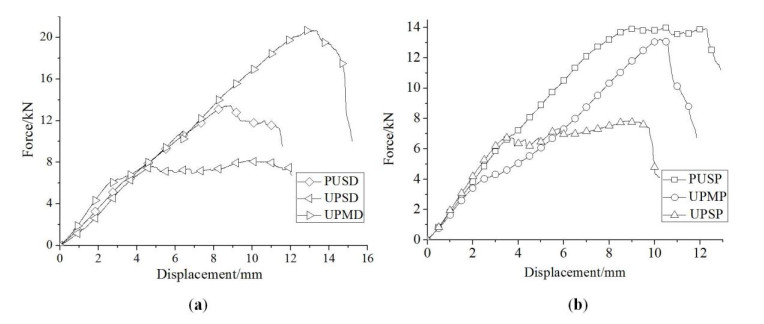
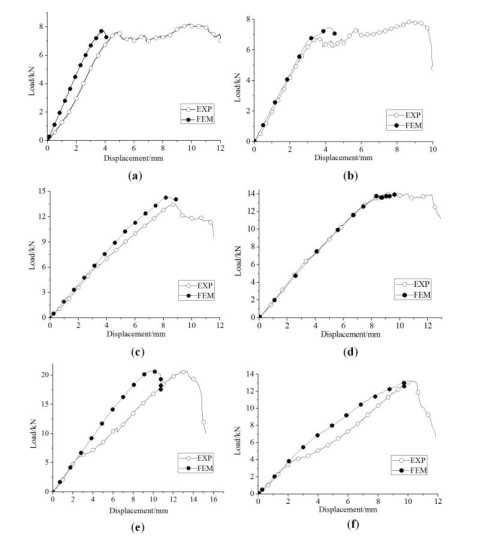
According to the experimental data, the pull-out load-displacement curve is plotted for the bolt joints of six specimens (Figure 3), with the equivalent yield point for each specimen indicated. It is shown in the figure that the load-displacement curve of each specimen shows similar characteristics. Before reaching the peak load, their stiffness variation can be divided into two phases: (1) the elastic phase, where stiffness is constant; (2) the stiffness reduction phase, where stiffness gradually declines. After the peak load, the load-displacement curve of each specimen displays a platform phase of a varying length, and the bearing capacity plummets after the platform phase.

Figure 3.  Load-displacement curves of specimens: (a) Specimens withdrilled holes; (b) Specimens with punched holes.

DownLoad: Full-Size Img PowerPoint

3.2.   Failure mode

According to the observation of the failure process of each specimen and analysis of the load-displacement curve, the damage to the bolted joints of the specimen displays the characteristics of a progressive failure. The damage characteristics of the material around the hole for each specimen are shown in Figure 4.

Figure 4.  The damage characteristics of specimens: (a) UPSP; (b) PUSD; (c) UPMD.

DownLoad: Full-Size Img PowerPoint

The uni-axial FRP specimens UPSD, UPSP, PUSD and PUSP exhibit similar failure modes, as shown in Figure 4(a) and (b). At the initial phase of loading, the specimens first undergo an elastic deformation phase, and a significant local depression around the hole. With the increase in displacement load, the specimens enter a phase in which the longitudinal splitting expands, during which, the pull-out stiffness decreases continually until reaching the equivalent yield. After the equivalent yield point being reached, the specimens enter a phase where the longitudinal fiber cracks around the hole, during which period, there appears a continuous fluctuation of or sustained decrease in the bearing capacity.

The multi-axial FRP specimens UPMD and UPMP also exhibit similar failure modes, as shown in Figure 4(c). At the initial phase of loading, the specimens first go through an elastic deformation phase, and experience an obvious local depression around the hole. Subsequently, they enter a phase where the shear cracks expand at an angle of ±45° and experience an interlaminar separation around the hole, also characterized by a continuous decrease in pull-out stiffness until the equivalent yield point is reached. After the equivalent yield point, they enter a shear cracking phase along the thickness direction of the fiber matrix, during which period, the pull-out bearing capacity of the specimen decreases continuously.

For all specimens, no pull-out failure occurs to the bolts from the initial loading till the final damage to the specimens, indicating that there still exists a certain surplus pull-out strength even after the materials around the hole have experienced a failure.

3.3.   Bearing capacity and pull-out ductility

The ultimate bearing capacity of each specimen and its corresponding displacement data and ductility coefficients are summarized in Table 3. The ultimate pull-out performance of the bolt takes the load value at the equivalent yield point on the load-displacement curve of each specimen.

Table 3.  Bearing capacity and ductility.

Specimens	Ultimate bearing capacity (kN)	Displacement (mm)	Ductility coefficient
UPSD	7.62 ± 0.57	4.82 ± 0.42	2.50 ± 0.26
UPSP	6.75 ± 0.64	3.58 ± 0.36	2.77 ± 0.30
PUSD	13.41 ± 0.86	8.60 ± 0.75	1.31 ± 0.16
PUSP	13.93 ± 0.92	8.93 ± 0.86	1.42 ± 0.23
UPMD	20.67 ± 1.49	12.93 ± 1.08	1.13 ± 0.11
UPMP	13.21 ± 0.85	10.22 ± 0.98	1.05 ± 0.13

---

 | Show Table

DownLoad: CSV

The ductility coefficient is an index for the plastic variable force of a structure or a component. The ductility coefficient μ_D of displacement is as expressed in Eq 1:

where D_y is deformation when the specimen begins to yield. This study takes the deformation corresponding to the ultimate load; D_u is deformation where the bearing capacity of the specimen does not decline significantly. This study takes the deformation that occurs at 0.85 times the ultimate bearing capacity.

The following conclusions can be drawn through comparing and analyzing the data in Table 3:

(1) There isn't much difference in the ultimate bearing capacity of the specimens UPSD and UPSP, and that of PUSD and PUSP, whereas the ultimate bearing capacity of the specimen UPMP declines by 36% compared with that of the specimen UPMD, indicating punching can greatly undermine the bearing capacity of the bolt holes of the multi-axial FRP. On the one hand, the stress around the hole is more concentrated on account of the oblong bolt hole. On the other hand, the punching process causes a great damage to the area around the bolt hole, causing the materials around the hole to fail in advance, and leading to the occurrence of progressive damage.

(2) The ultimate bearing capacity of the specimen PUSD is improved by 76% as compared to that of the specimen UPSD, and the ultimate bearing capacity of the specimen PUSP is improved by 106% as compared to that of the specimen UPSP, indicating that the improvement in performance of the resin matrix can effectively enhance the ultimate bearing capacity of the specimen.

(3) The ultimate bearing capacity of the specimen UPMD is improved 2.7 and 1.5 times as against the specimens UPSD and PUSD, respectively, indicating that the multi-axial fiber is conducive to facilitate the ultimate bearing capacity of the specimens with drilled holes.

(4) The pull-out ductility of the specimens UPSD and UPSP are significantly superior to other specimens in this respect.

4.   Numerical simulation

The universal finite element software ABAQUS6.14-4 is used to simulate the specimen loading process. Combined with the PDA method, this study gives predictions concerning the pull-out performance of the bolted joints.

4.1.   Finite element model

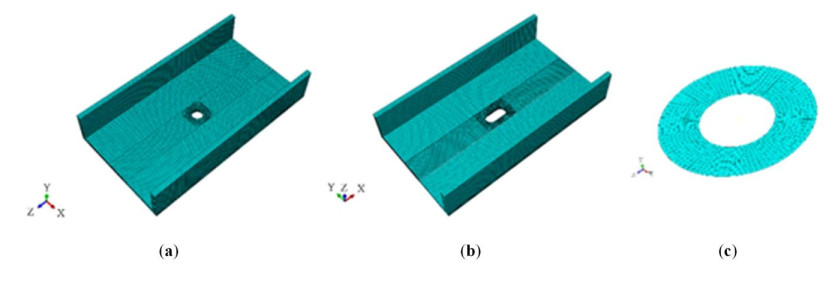
The finite element models for the specimens with drilled holes or punched holes are shown in Figure 5(a) and (b), respectively, in which, the composite profiles adopt the C3D8R solid element for simulation. The C3D8R solid element is a linear reduced integral element, can generate accurate displacement results, and thereby is suitable for specimens whose grids are severely distorted, and can effectively simulate the mechanical behavior of the composite profiles under the action of shear load ^[16]. To simulate the longitudinal crack generated during the loading process of the specimen, contact pairs are introduced at the corresponding position on the specimen. By setting their cohesive properties, the opening mode, sliding mode and tearing mode cracks can be simulated in the fracture mechanics ^[17]. The adoption of the cohesive properties of contact pairs to simulate the cracking behavior of the material does not require inserting additional elements, thereby having little impact on the stress distribution around contact pairs, and making the simulation approximate to the real situation. The contact surface between the specimen and the support is simulated by the contact pair. The contact belongs to hard contact, and the friction between the surfaces adopts the penalty friction. The bolt, whose inner and outer ring radii are 6 and 12.5 mm respectively, is simplified as a rigid ring surface (Figure 5(c)). Ignoring the interaction between the bolt rod and hole wall, contact pairs are only established with the bolt hole surface of the specimen. The contact belongs a hard contact, and the friction between the surfaces adopts the penalty friction. Finally, the displacement load is applied through this rigid ring.

Figure 5.  The finiteelement models of specimens: (a) Specimens withdrilled holes; (b) Specimens with punched holes; (c) Rigid ring surface.

DownLoad: Full-Size Img PowerPoint

For the constitutive setting of the finite element model, it is assumed that the single layer of the FRP is a transversely isotropic body, then the modulus parameter satisfies Eqs 2-6 ^[18]:

Generally, υ₁₂ = 0.33. The elastic constants can be derived by combining the material data in Table 2.

The strength parameters satisfy Eqs 7-9:

Given the strength data in Table 2, nine strength parameters can be obtained.

The material constitutive parameters of the finite element model are summarized in Table 4 for the three types of specimens.

Table 4.  Material properties of finite element models.

Specimens	UPSD, UPSP	PUSD, PUSP	UPMD, UPMP
Longitudinal modulus, E1 (GPa)	20.45	24.40	18.20
Transverse modulus, E2 (GPa)	8.80	11.20	5.10
Transverse modulus, E3 (GPa)	8.80	11.20	5.10
In-plane shear modulus, G12 (GPa)	4.90	6.10	2.35
Out-of-plane shear modulus, G13 (GPa)	1.69	2.07	0.80
Out-of-plane shear modulus, G23 (GPa)	1.69	2.07	0.80
Major Poisson's ratio, υ12	0.33	0.33	0.33
Through thickness Poisson's ratio, υ13	0.33	0.33	0.33
Through thickness Poisson's ratio, υ23	0.454	0.453	0.474
Longitudinal tensile strength, XT (MPa)	2550	3020	2360
Transverse tensile strength, YT (MPa)	180	340	170
Transverse tensile strength, ZT (MPa)	180	340	170
Longitudinal compression strength, XC (MPa)	1560	1747	1340
Transverse compression strength, YC (MPa)	250	460	230
Transverse compression strength, ZC (MPa)	250	460	230
In plane shear strength, S12 (MPa)	96	158	140
Out-of-plane shear strength, S13 (MPa)	50	78	19
Out-of-plane shear strength, S23 (MPa)	50	78	19

---

 | Show Table

DownLoad: CSV

4.2.   Failure criteria and degradation models

Due to the anisotropic properties of the composite profiles, their failure mechanism is quite complicated, making it difficult to judge their failure by adopting a simple uniform failure criterion. Common failure criteria include Tsai-Wu tensor criterion, Hashin failure criterion, Yamada-sun failure criterion, etc., among which, the Hashin failure criterion is a mode-related failure criterion ^[19], as it provides not only the conditions, but also the mode for material failure. Therefore, this criterion is adopted in the finite element simulation in this study. The specific expressions are as expressed in Eqs 10-16:

(1) Fiber tensile failure (σ₁ > 0)

(2) Fiber compression failure (σ₁ < 0)

(3) Matrix tensile failure (σ₁ > 0)

(4) Matrix compression failure (σ₂ < 0)

(5) Matrix fiber shear failure (σ₁ < 0)

(6) Tensile delamination failure (σ₃ > 0)

(7) Compression delamination failure (σ₃ < 0)

The material stiffness degradation model, corresponding to the Hashin failure criterion, is based on the Camanho degradation model ^[20]. The material stiffness degradation model is realized by means of the reduction factor, taking the degradation of elastic modulus, shear modulus and Poisson's ratio into account. For different materials, the value of the reduction factor is usually different. With reference to Warren ^[21], Kong ^[22], A Du ^[23], and others' researches, the material reduction factor of the three specimens is selected according to Table 5 in this study.

Table 5.  Degradation parameters.

Specimens	UPSD, UPSP	PUSD, PUSP	UPMD, UPMP
Fiber tensile failure	E1D=0.01E1 ν12D=0.01ν12 ν13D=0.01ν13 ν23D=0.01ν23	E1D=0.08E1 ν12D=0.08ν12 ν13D=0.08ν13 ν23D=0.08ν23	E1D=0.01E1 ν12D=0.01ν12 ν13D=0.01ν13 ν23D=0.01ν23
Fiber compression failure	E1D=0.065E1 ν12D=0.01ν12 ν13D=0.01ν13 ν23D=0.01ν23	E1D=0.065E1 ν12D=0.08ν12 ν13D=0.08ν13 ν23D=0.08ν23	E1D=0.065E1 ν12D=0.01ν12 ν13D=0.01ν13 ν23D=0.01ν23
Matrix tensile or compression failure	E2D=0.01E2 G12D=0.01G12 G23D=0.01G23 ν12D=0.01ν12 ν23D=0.01ν23	E2D=0.08E2 G12D=0.08G12 G23D=0.08G23 ν12D=0.08ν12 ν23D=0.08ν23	E2D=0.01E2 G12D=0.01G12 G23D=0.01G23 ν12D=0.01ν12 ν23D=0.01ν23
Tensile or compression delamination failure	E3D=0.01E3 G13D=0.01G13 G23D=0.01G23 ν13D=0.01ν13 ν23D=0.01ν23	E3D=0.08E3 G13D=0.08G13 G23D=0.08G23 ν13D=0.08ν13 ν23D=0.08ν23	E3D=0.19E3 G13D=0.19G13 G23D=0.19G23 ν13D=0.19ν13 ν23D=0.19ν23
Matrix fiber shear failure	G12D=0.08G12 G13D=0.08G13 G23D=0.08G23 ν12D=0.08ν12 ν13D=0.08ν13 ν23D=0.08ν23	G12D=0.4G12 G13D=0.4G13 G23D=0.4G23 ν12D=0.4ν12 ν13D=0.4ν13 ν23D=0.4ν23	G12D=0.01G12 G13D=0.01G13 G23D=0.01G23 ν12D=0.01ν12 ν13D=0.01ν13 ν23D=0.01ν23

---

 | Show Table

DownLoad: CSV

4.3.   Load-displacement curves

By establishing a sophisticated finite element analysis model, combined with the above material failure criterion and material degradation model, we conduct the progressive damage analysis of the pull-out process of the bolted joints of each specimen, and obtain the load-displacement curve for each specimen, as shown in Figure 6 (a), (b), (c), (d), (e), and (f), respectively, which are compared with those obtained from the experiment. The errors between the simulated prediction results and the experimental results are summarized in Table 6. It is clear that the simulation curve of each specimen displays characteristics in three phases, namely: (1) linear elastic phase; (2) around-the-hole crack expansion phase; (3) bearing capacity declining phase. The predicted curves always tend to be consistent with the experimental curves. Since the finite element model in this study does not take the initial damage to the material around the bolt hole into consideration, there are deviations to some extent between the predicted equivalent yield point from the experimental equivalent yield point. However, in general, the PDA method can effectively simulate the pull-out process of the bolt.

Figure 6.  The finiteelement models of specimens: (a) UPSD; (b) UPSP; (c) PUSD; (d) PUSP; (e) UPMD; (f) UPMP.

DownLoad: Full-Size Img PowerPoint

Table 6.  Deviation analysis.

Specimens	Ultimate bearing capacity (kN)		Deviation	Displacement (mm)		Deviation
	EXP	FEM		EXP	FEM
UPSD	7.62 ± 0.57	7.75	1.7%	4.82 ± 0.42	3.81	-20.9%
UPSP	6.75 ± 0.64	6.77	0.3%	3.58 ± 0.36	3.19	-10%
PUSD	13.41 ± 0.86	14.32	6.8%	8.60 ± 0.75	8.26	-4.0%
PUSP	13.93 ± 0.92	13.84	-0.5%	8.93 ± 0.86	8.99	0.7%
UPMD	20.67 ± 1.49	20.77	0.5%	12.93 ± 1.08	9.94	-23.1%
UPMP	13.21 ± 0.85	13.01	-1.5%	10.22 ± 0.98	9.73	-4.8%
Notes: EXP, experimental specimens. FEM, the value based on finite element method. Deviation is the percentage based on the difference between the average of the values of the EXPs and that of the value obtained based on the FEM.

---

 | Show Table

DownLoad: CSV

4.4.   Distribution of stress around the bolt holes

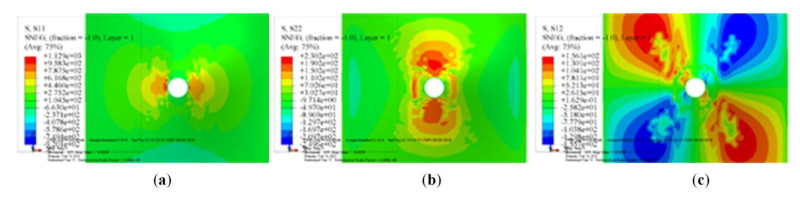
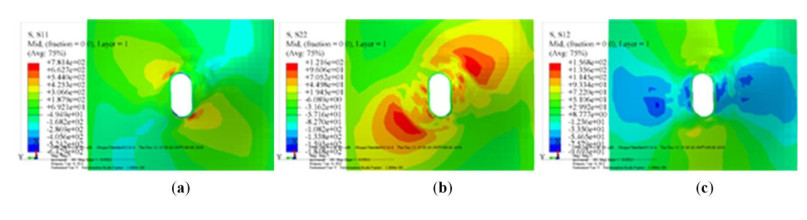
The anisotropic stress nephograms around the hole for the two typical specimens PUSD and UPMP under the peak load are shown in Figure 7 and Figure 8, respectively. From the stress nephogram, it is obvious that the stress distribution around the bolt hole under the action of peak load is very complicated. The adoption of the PDA method predicts the damage to the material around the hole and reduces the stiffness of the element accordingly, so that the value of the stress in the damage area is significantly lower than that in the surrounding undamaged area.

Figure 7.  The stress nephograms of PUSD:(a) Longitudinal stress; (b) Transverse stress; (c) In plane shear stress.

DownLoad: Full-Size Img PowerPoint

Figure 8.  The stress nephograms of UPMP: (a) Longitudinal stress; (b) Transverse stress; (c) In plane shear stress.

DownLoad: Full-Size Img PowerPoint

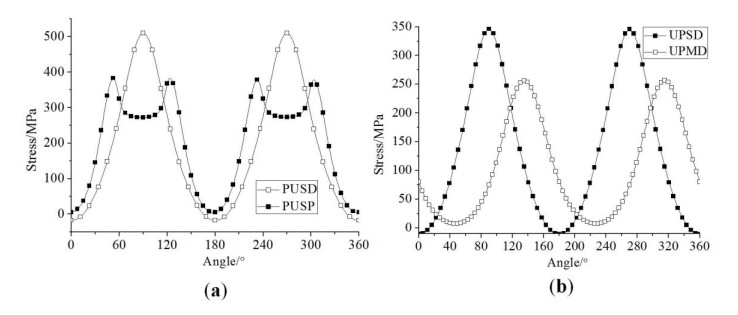
To compare the impact of bolt hole shape and fiber direction on the stress distribution around the hole, we use the bolt hole side as the stress path, and plot the distribution curve of the longitudinal stress around the hole when the bolt displacement is 3 mm for the specimens PUSD and PUSP, and 2.25 mm for the specimens UPSD and UPMD in Figure 9(a) and (b) respectively. In the figure, the zero direction is the pultrusion direction. In Figure 9(a), there is a significant difference between these two specimens in that longitudinal stresses around the hole are concentrated in a different manner. For the round hole, the stresses concentrate on the 90°and 270°positions, and for the oblong hole, they concentrate on the four intersections between the long and short sides. It can be seen from Figure 9(b) that, due to the influence of fiber direction, stresses around the hole in the specimen UPMD concentrate approximately on 135° and 315° positions, deviating a little from those in the specimen UPSD, with a deviation angle of 45°.

Figure 9.  The distribution curve of the longitudinal stress around the holes: (a) PUSD and PUSP; (b) UPSD and UPMD.

DownLoad: Full-Size Img PowerPoint

5.   Conclusion

This study conducts experiments on the pull-out performance of bolted joints with drilled or punched holes on FRP specimens respectively, and performs a finite element analysis. The following conclusions are arrived at:

(1) There isn't much difference in the pull-out performance of bolted joints on the uni-axial pultruded FRP specimens (PUSD, UPSD) with drilled holes and the uni-axial pultruded FRP specimens (PUSP, UPSP) with punched holes. The bolt hole shape and hole-opening method exert little impact on their pull-out performance, and both hole-opening methods apply to this type of material. However, the ultimate pull-out performance of bolted joints on the multi-axial pultruded FRP specimen (UPMP) with punched holes is significantly lower than that of bolted joints on the multi-axial pultruded FRP specimen (UPMD) with drilled holes. The main reason is that the punching method has caused a big initial damage to the multi-axial FRP, and the impact of stress concentration resulted from the oblong hole shape is also bigger than that on the uni-axial pultruded FRP. However, its bearing capacity is still on the same level as that of the specimen PUSP, indicating that the punching method can also be applied to the multi-axial FRP to some extent.

(2) For different types of PFRP, we make bolt holes by both the drilling and punching method. The experiment on the pull-out performance of bolted joints reveals different failure modes: the failure characteristics for the uni-axial PFRP specimens PUSD, PUSP, UPSD and UPSP belong to the longitudinal tearing cracks and their further expansion. The failure characteristics for the multi-axial PFRP specimens UPMD and UPMP belong to the 45° oblique cracks and their further expansion with a local shear damage to materials in the stress concentrated area.

(3) The pull-out performance of bolted joints for different types of pultruded profiles differs quite a lot. The pull-out bearing capacity of the specimens UPSD, PUSD and UPMD with drilled holes is 7.62, 13.41, and 20.67 kN, respectively. The pull-out bearing capacity of specimens UPSP, PUSP and UPMP with punched holes is 6.75 kN, 13.93 kN and 13.21 kN, respectively. The above differences are mainly attributed to the fact that the mechanical properties of the polyurethane resin matrix are better than the unsaturated polyester resin. As a result, the ultimate bearing capacity of specimen PUSD is better than that of UPSD, and similarly, the ultimate bearing capacity of PUSP is better than that of UPSP. The fiber at an angle of 45° and 90° enhances the transverse strength of the specimen UPMD, effectively preventing the occurrence of longitudinal cracks, and making its ultimate bearing capacity superior to those of the specimens PUSD and UPSD.

(4) The finite element software ABAQUS6.14-4 is adopted in this study, combined with the PDA method, to simulate the pull-out performance of the bolted joints on PFRP with punched holes. The simulation results are in good agreement with the experiment results, indicating that the finite element simulation method is applicable to the simulation and prediction of bolted joints on PFRP.

Acknowledgments

This research was funded by National Key R & D Program of China (2017YFC0703006) and the National Natural Science Foundation of China (Grant No. 51778286) and the Natural Science Foundation of Jiangsu Province (Grant No. BK20171469).

Conflict of interest

The authors declare no conflict of interest in this paper.