Force transmission characteristics in a multiple-fulcrum supporting platform with heavy loads

1.   Introduction

For the force transmission characteristics of mechanism, Gan studied the force transmission characteristics of a metamorphic parallel mechanism (MPM) with reconfigurable 3T and 3R motions ^[1,2,3]. Dai proved the relationship between the screw system and its reciprocal system by combining linear algebra and advanced kinematics theory, and obtained some physical properties of the screw system ^[4,5]. These studies on the force transmission characteristics of the above mechanism analyzed the corresponding relationship between different positions of the actuator in space and the output force from the perspective of dynamics. Given that it is a dynamic question, the corresponding relationship between the spatial position and the output force is dynamic ^[6], and finding a stable state to establish the relationship between the two is difficult. When the output force of the end-effector is equal, the conditions needed by the spatial position of the actuators to meet with a unified relation are not easy to describe. Therefore, from the perspective of dynamics, the special force transmission relationship between the spatial position of the actuator and the output force (such as the spatial position relationship of the actuator corresponding to the equal output force) is complicated. It provides a new way of thinking for studying some special force transmission relations from the perspective of statics.

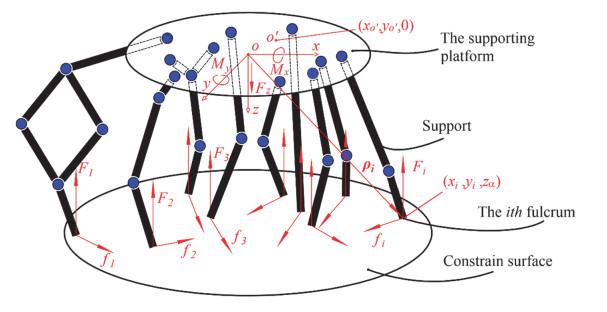
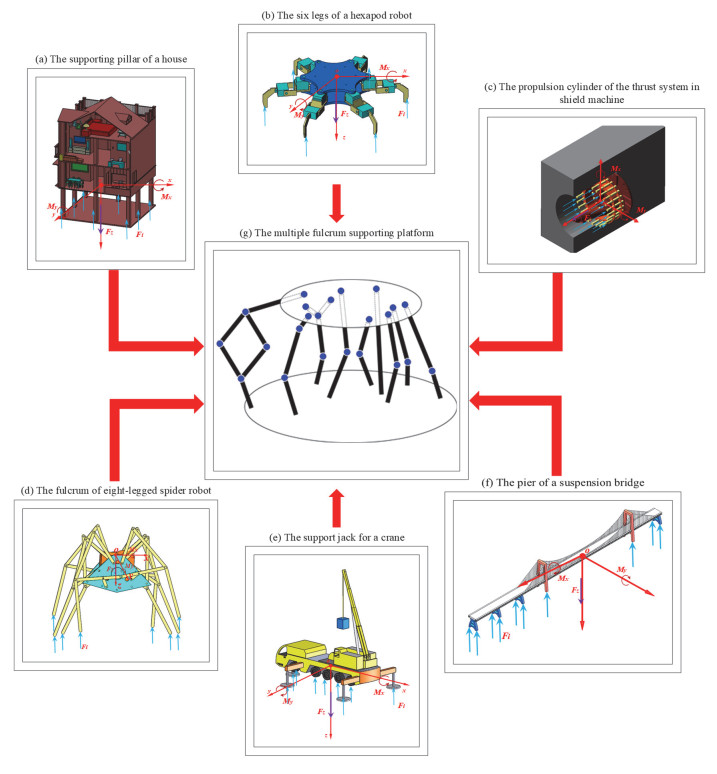
In vehicle engineering, the crane adopts the layout of jacks shown in Figure 1e to support the car body and prevent it from rolling over, and the truck often adopts the structure form of the rear eight wheels to provide support and prevent severe deformation of the tire due to excessive load. In shield machine construction, the hydraulic cylinder of the shield propulsion system is designed and optimized with the non-equidistant layout depicted in Figure 1c to reduce the influence caused by partial load effectively and prevent the rupture and collapse of the rear pipe segments caused by excessive partial load ^[7,8]. In civil engineering, the ground floor is often supported by the distribution of pillars in Figure 1a to increase the carrying capacity of the house. In robot research, the zero moment point is an important indicator to determine the dynamic and stable motion of robots ^[9,10,11]. The supporting part of the hexapod robot is often in the form of a circular uniform layout as shown in Figure 1b and the fulcrum of eight-legged spider robot is often in the form of layout described in Figure 1d to ensure the stability of the main body ^[12]. In other fields, suspension bridges are often supported as shown in Figure 1f to allow vehicles to cross the river ^[13]. The above discussion shows that crane jacks, truck tires, hydraulic cylinders in the shield propulsion system, the support structure of hexapod robot and eight-legged spider robot, pillars of house and the pier of suspension bridge have the same characteristics. That is, the external combined resistance and the supporting forces acting on all fulcrums are parallel and perpendicular to the same surface, and the vertical stiffness of all supporting structures remains the same. As shown in Figure 1g, the structure with the above typical characteristics is the multiple-fulcrum supporting platform, the part acted by the supporting force is the support, the point on which the supporting force acts is the fulcrum, and the distribution plane in which all fulcrums can be reconfigured is the constraint surface.

From the perspective of structural mechanics, when a multiple-fulcrum supporting platform is subjected to external loads, the distribution of forces on all fulcrums not only satisfies the equilibrium condition of Newton's second law ^[14,15] but also distributes forces in a way that makes the whole system achieve the minimum energy, that is, the Hamiltonian principle ^[16,17]. Under specific external loads, the force transmission characteristics of the multiple-fulcrum supporting platform will constantly change with the different layout positions of its fulcrums on the constraint surface. If the layout positions of the fulcrums are reconfigured so that the supporting forces provided by these fulcrums are all equal, the force transmission performance of the multiple-fulcrum supporting platform reaches the optimal when the vertical deformation of each support remains consistent, and the energy consumption of all supports achieves the minimum. The characteristics of the above optimal force transmission have the following general functions in practical engineering: ensure that the wear degree of each support is basically consistent, avoid some supports bearing too much to cause rupture, ensure that all supports are in the lowest energy state under the action of the external force, and prevent the supporting platform from turning over. In addition to the above general functions, the characteristics of the optimal force transmission of the multiple-fulcrum supporting platform in specific engineering applications also have special functions. For example, when the hydraulic cylinder of the shield propulsion system is in the optimal force transmission, all the hydraulic cylinders exert the same jacking force on the rear segments, which can effectively avoid the crushing of the rear segments due to excessive partial load ^[18,19]. Again for example, in one area, the load-bearing wall of a high-rise building was torn down and the whole house collapsed. It is assumed that the load-bearing column of the house can achieve the optimal force transmission performance by adding a certain load-bearing column under the condition that there is no load-bearing wall, and if the load-bearing wall is knocked down unintentionally, the whole house will not collapse due to the support function of the new added load-bearing column ^[20].

Considering the above-mentioned advantages of optimal force transmission, the present study focuses on how to realize the optimal force transmission of the multiple-fulcrum supporting platform by reconfiguring the position of the fulcrum under specific external loads. Therefore, the optimal force transmission model and force transmission characteristic model of the multiple-fulcrum supporting platform are established. Some layout reconfiguration methods to achieve the optimal force transmission performance of the platform are proposed, and relevant conclusions are drawn by applying these layout reconfiguration methods, which are described in detail in the following sections.

2.   Materials and methods

2.1.   Force transmission model of the multiple-fulcrum supporting platform

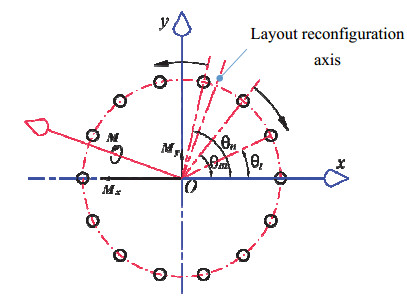
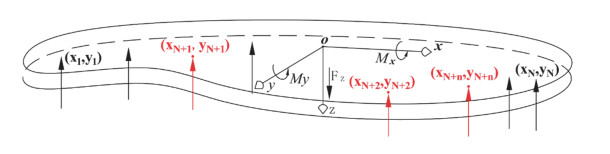
The constraint surface where the fulcrum is located is depicted in Figure 2. The external loads on the supporting platform are F_z, M_x, and M_y (the external loads acting on the coordinate origin o can be represented as F_z, M_x, and M_y). By taking the geometric center of the supporting platform as the coordinate origin o, the z-axis is parallel to all supporting forces, the y-axis is vertical to the z-axis and points to the direction depicted in Figure 2, and the direction of the x-axis is decided by the right-hand rule ^[21] to establish the Cartesian coordinate system o-xyz. As described in Figure 2, M_y is the external combined resistance moment along the positive direction of the y-axis; M_x is the external combined resistance moment along the positive direction of the x-axis; M is the external combined resistance moment; F_z is the external combined resistance along the positive direction of the z-axis; and F_i (i = 1, 2, 3, ..., N) is the supporting force provided by the i^th fulcrum, whose direction is opposite to that of F_z; f_i is the friction on the i^th fulcrum; The structure has N supports, and the vertical stiffness coefficient of each support is k.

Three static equilibrium equations of (1)–(3) can be obtained according to the force on the multiple-fulcrum supporting platform in Figure 2:

where ρ_i is the polar radial vector of the i^th fulcrum shown in Figure 2.

According to the principle of minimum energy ^[22,23], the lower the energy, the more stable the system. Eqs (1)–(3) are used as the basis to construct the optimization function (4) and minimize the energy of all supports. Supports can reach static equilibrium very quickly because the deformation of all supports is small and the damping is large ^[24,25]. In this process, the kinetic energy of the whole system eventually tends to zero, and the gravitational potential energy decreases while the elastic potential energy increases. Therefore, the establishment of Eq (4) only needs to consider the situation when the elastic potential energy of the system achieves the minimum.

where $\Delta {l_i}$ is the vertical deformation generated by the i^th fulcrum, and $\Delta {l_i} = {{{F_i}} / k}$.

If W in the optimization function (4) achieves the minimum value, then all supports in the multiple-fulcrum supporting platform have the minimum energy, and the system is in the most stable state, which is conducive to saving the overall energy consumption of the system.

Using simultaneous optimization function (4) and static equilibrium Eqs (1)–(3), we can construct the Lagrange function of Eq (5) as follows ^[26]:

where ${\lambda _{\, 1}}, \; {\lambda _{\, 2}}, \; {\lambda _{\, 3}}$ are the Lagrange parameters; (x_i, y_i) refers to the coordinate point of force provided by each fulcrum in the o-xy plane.

The partial derivatives of Lagrange equation (5) are calculated to obtain Eqs (6) and (7):

On the ground of Eqs (6) and (7), the matrix equation can be gained as follows:

Assume that matrix D is the inverse matrix of the coefficient matrix of Eq (8), and let it be

and

Solving Eq (9) obtains the following Lagrange parameters ${\lambda _{\, 2}}$ and ${\lambda _{\, 3}}$:

Considering the relationship between matrix D and its own invertible matrix ^[27], we can acquire,

From Eq (12), the following equations can be deduced:

Substituting Eq (13) into Eqs (14) and (15) obtains the following two equations:

In a uniform force system, when the supporting force is equal to each other, the following equation must be built:

Substituting Eq (18) into Eq (7) obtains

The above derivation process manifests that Eq (19) must be true when the supporting forces provided by fulcrums are all equal. On the premise of the principle of minimum energy, if Eq (19) is true, then the supporting forces provided by all fulcrums must be equal.

Substituting Eq (19) into Eqs (16) and (17) achieves

Substituting Eqs (20) and (21) into Eqs (10) and (11) results in the following equation:

On the ground of Eq (8), the following equation can be deduced:

Substituting Eq (22) into Eq (23) acquires

Substituting Eqs (22) and (24) into Eq (6) establishes Eq (18), that is, the supporting force provided by each fulcrum is equal.

The force translation theorem of statics ^[28,29] states that an additional torque is generated when a force transfers from one point to another in space. As depicted in Figure 2, a point ${o'}$ with a coordinate of $\left({{x_{{o'}}}, {y_{{o'}}}} \right)$ exists in the o-xy plane of the constructed Cartesian coordinate system o-xyz, so that the effect of external loads F_z, M_x, and M_y can be replaced by the external combined resistance F_z acting on this point called the force equivalent point (FEP). At this moment,

Transforming Eq (19) obtains

where $\overline x = {{\sum\limits_{i = 1}^N {{x_i}} } / N}\; , \; \overline y = {{\sum\limits_{i = 1}^N {{y_i}} } / N}$, the point represented by the coordinate $\left({\overline x \, , \, \overline y } \right)$ is called the layout central point (LCP).

As demonstrated in Eqs (19), (25), and (26), when the FEP coincides with the LCP, namely ${x_{{o'}}} = \overline x \; , \; {y_{{o'}}} = \overline y$, the supporting forces provided by all fulcrums are equal, which prevents some supports from collapsing under excessive pressure and saves energy. In this study, the finding that all the supporting forces provided by the fulcrums are equal when the FEP coincides with the LCP is named as the law of uniform force characteristics of the multiple-fulcrum supporting platform.

2.2.   Force transmission characteristics of typical multiple-fulcrum supporting platform

In the Section 2.1, the optimal force transmission of the multiple-fulcrum supporting platform has been discussed. In the following part, the force transmission characteristics of the platform for constraint surfaces with three common shapes are discussed.

2.2.1.   Force transmission characteristics of the multiple-fulcrum supporting platform with rectangular or square constrained surface

As shown in Figure 2, the distribution of the fulcrum (x_i, y_i, z_α) on the constraint surfaceα: z = z_α satisfies the following equation:

where p and q respectively represent the length and width of the rectangle. When p is equal to q, they represent the side length of the square.

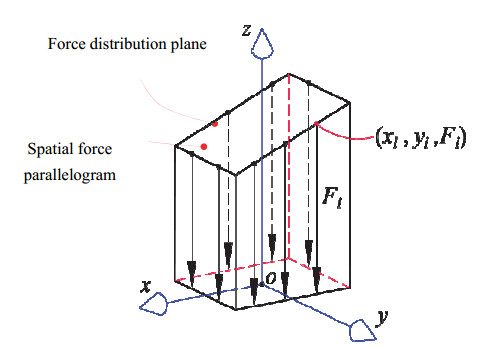
If the spatial distribution of the supporting force provided by each fulcrum can be solved, then the Cartesian coordinate system shown in Figure 3 needs to be established with variables F_i, x, and y as axes. Combining the plane Eq (6) and the rectangular cylindrical Eq (29) shows that the solution of F_i must be on the intersection line of the two space surfaces, and the spatial parallelogram plane formed by the intersection line is called the force distribution plane (FDP). The specific expression is as follows:

where ${\lambda _{\, c}} = {{\left({{d_{N + i1}}{F_z} - {d_{N + i2}}{M_y} + {d_{N + i3}}{M_x}} \right)} / k}, \; \left({c = 1\; , \; 2\; , \; 3} \right)$.

As shown in Figure 3, the maximum and minimum values of the supporting force must appear at the two diagonal vertices of the spatial parallelogram, and the coordinate of the central symmetric point about the force distribution plane of spatial parallelogram is $\left({0, \; 0, \; - k{\lambda _{\, 1}}} \right)$. The geometric characteristics of the spatial force parallelogram can be completely determined by the above description. Under the condition of the external loads and the layout position of each fulcrum given, the supporting force provided by each fulcrum can be calculated by Eq (30).

2.2.2.   Force transmission characteristics of the multiple-fulcrum structure with circular constraint surface

The distribution of the fulcrum (x_i, y_i, z_α) on the constraint surfaceα: z = z_α satisfies the following equation:

where r is the radius of the circle.

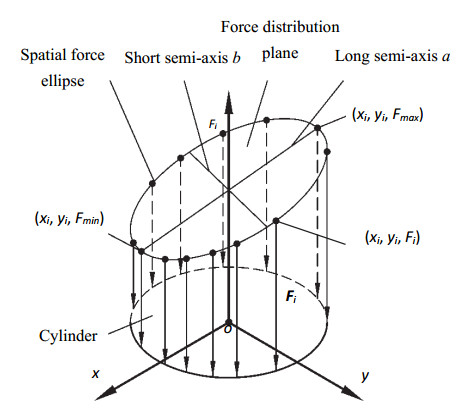
In the same way, the Cartesian coordinate system shown in Figure 4 is established with variables F_i, x, and y as axes. Combining the plane Eq (6) and cylinder Eq (31) shows that the solution of F_i must be on the intersection line of the two space surfaces.

On the basis of the analysis, the maximum and minimum values of the supporting force in this case are as follows:

On the basis of Eqs (32) and (33), three parameters of the spatial ellipse force distribution plane can be obtained as follows:

where a, b, and e are the long semi-axis, short semi-axis, and eccentricity of the spatial ellipse force distribution plane, respectively.

Transforming Eq (36) obtains

Substituting Eqs (10) and (11) into Eq (37) achieves

Eq (38) indicates that in the Cartesian coordinate system with variables F_z, M_x, and M_y as the axes, an ellipse can be formed according to Eq (38) in the plane o-M_xM_y when the external resistance F_z and eccentricity e are given.

2.3.   Layout reconfiguration method for the uniform force characteristics of the multiple-fulcrum supporting platform under different types of constrained surface

For different types of constrained surface, reconfiguration methods of the uniform force characteristics of the multiple-fulcrum supporting platform are different. Reconfiguration difficulty and energy consumption can be greatly reduced to achieve force uniformity effectively by reconfiguring as few layout positions of the fulcrums as possible and shortening the adjustment range of the fulcrum. The specific implementation method is described below.

2.3.1.   Layout reconfiguration method for uniform force characteristics of the multiple-fulcrum supporting platform under rectangular constraint surface

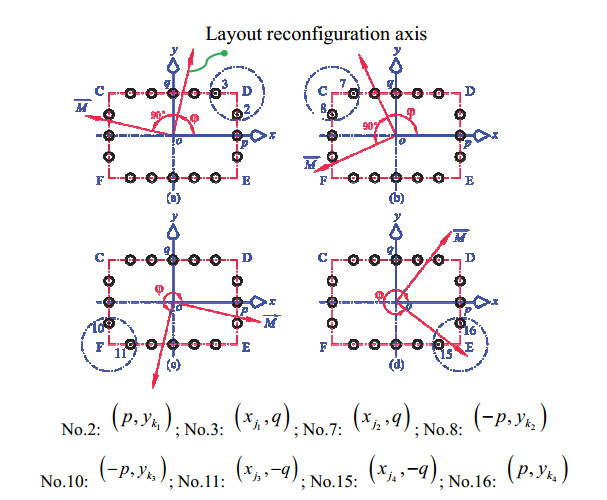
Suppose the geometric center of the rectangular constraint surface is at the origin of the o-xy plane. The four vertices of the rectangular constraint surface are C, D, E, and F as shown in Figure 5. The expression of line l_CD is y = q (q > 0), and the expression of line l_DE is x = p (p > 0). Similarly, the expression of line l_EF is y = −q, and the expression of line l_CF is x = −p. If the direction of the external combined resistance moment M is depicted in Figure 5, then the straight line obtained by clockwise rotating π/2 along the direction of M is called the layout reconfiguration axis, and the angle between the positive direction of the x-axis and the layout reconfiguration axis is φ. Before adjustment, each fulcrum is in uniform distribution, and the following equation must be acquired:

In Figure 5 (a)–(d), when, the coordinate positions $\left({{x_{{j_s}}}, \sqrt 2 q\, \cdot \, \cos \left[{{\pi / 4} + \left({s - 1} \right)\, \cdot {\pi / 2}} \right]} \right)$ and $\left({\sqrt 2 p\, \cdot sin\left[{{\pi / 4} + \left({s - 1} \right)\, \cdot {\pi / 2}} \right], {y_{{k_s}}}} \right)$ of the two fulcrums are selected for adjustment, while the positions of other fulcrums remain unchanged. As depicted in Eqs (19) and (39), when the following equation is satisfied, the supporting force provided by each fulcrum is equal.

where $\left({x_{{j_s}}', \sqrt 2 q\, \cdot \, \cos \left[{{\pi / 4} + \left({s - 1} \right)\, \cdot {\pi / 2}} \right]} \right)$ and $\left({\sqrt 2 p\, \cdot \, sin\left[{{\pi / 4} + \left({s - 1} \right)\, \cdot {\pi / 2}} \right], y_{{k_s}}'} \right)$ are the adjusted coordinates of the two corresponding fulcrums $\left({{x_{{j_s}}}, \sqrt 2 q\, \cdot \, \cos \left[{{\pi / 4} + \left({s - 1} \right)\, \cdot {\pi / 2}} \right]} \right)$ and $\left({\sqrt 2 p\, \cdot \, sin\left[{{\pi / 4} + \left({s - 1} \right)\, \cdot {\pi / 2}} \right], {y_{{k_s}}}} \right)$, respectively.

2.3.2.   Layout reconfiguration method for the uniform force characteristics of the multiple-fulcrum supporting platform under circular constraint surface

When all fulcrums of the multiple-fulcrum supporting platform are uniformly distributed under the circular constraint surface, the layout phase angle of each fulcrum shown in Figure 6 satisfies the following equation:

where θ_t refers to the angle between the radius r of the circular constraint surface and the positive direction of the x-axis.

Transformation of Eqs (41) and (42) obtains

where θ_t (t = 1, 2, …, N and t ≠ m, n), θ_m and θ_n are the layout phase angles when all fulcrums are uniformly distributed.

When the multiple-fulcrum supporting platform is subjected to external loads shown in Figure 6, the positions of θ_m and θ_n are adjusted to θ_m^' and θ_n^', respectively, where θ_m and θ_n are the layout phase angles of adjacent fulcrums on both sides of the layout reconfiguration axis obtained by clockwise rotating 90° along the external combined resistance moment M shown in Figure 6, and the positions of other fulcrums are unchanged. The following equations can be established by combining Eqs (43) and (44). At this time, all the supporting forces provided by all fulcrums are equal.

2.3.3.   Layout reconfiguration method for uniform force characteristics of the multiple-fulcrum supporting platform under unconstrained surface

As shown in Figure 7, suppose N fulcrums are present in the multiple fulcrum supporting platform, among which the position of N-n fulcrums remains original, and the position of the j^th (j = u, u+1, …, u+n-1) fulcrum changes from the original coordinate $\left({{x_j}, {y_j}} \right)$ to $\left({x_j', y_j'} \right)$, so that the adjusted LCP of the structure coincides with the FEP. The specific elaboration is as follows:

After adjustment, the following formula can be established:

Through adjusting the position of some fulcrums, the supporting force provided by each fulcrum can be equal. This method does not increase the number of fulcrums in the structure. Thus, it is called "displacement reconfiguration method."

On the basis of the relationship between the number of equations and the unknowns, Eq (19) can solve two unknowns. Thus, the following formula can be established:

Eq (48) indicates that the supporting force provided by each fulcrum can also be equal by adjusting only the position of a certain fulcrum $\left({{x_u}, {y_u}} \right)$ to $\left({x_u', y_u'} \right)$.

As shown in Figure 8, the original N fulcrums of the multiple-fulcrum supporting platform are assumed to remain unchanged. When fulcrums are added and reach the coordinate position $\left({{x_v}, {y_v}} \right)$ (v = N+1, N+2, …, N+n), the LCP of the structure only coincides with the FEP. The specific elaboration is as follows:

After adjustment, the following formula can be established:

In this method, the supporting force of each fulcrum is equal by adding some fulcrums and then adjusting the positions of the fulcrums. This reconfiguration method needs to adjust the position of the newly added fulcrums. Thus, it is called "reconfiguration method combined by number and displacement."

On the bases of the relationship between the number of equations and the unknowns, Eq (19) can solve two unknowns. Thus, the following formula can be established:

Eq (50) reveals that the supporting force provided by each fulcrum can also be equal by adding a fulcrum $\left({{x_v}, {y_v}} \right)$ and then adjusting the position of the fulcrum.

3.   Results

In section 2.3, layout reconfiguration methods are proposed for different types of constraint surfaces. However, in the engineering application, the above layout reconfiguration methods should be combined with the actual engineering background of the multiple-fulcrum supporting platform. The following is an illustration about the application of the layout reconfiguration methods to realize the uniform force characteristics of the multiple-fulcrum supporting platform.

3.1.   Application of layout reconfiguration methods for uniform force characteristics of the support structure of a truck under rectangular constraint surface

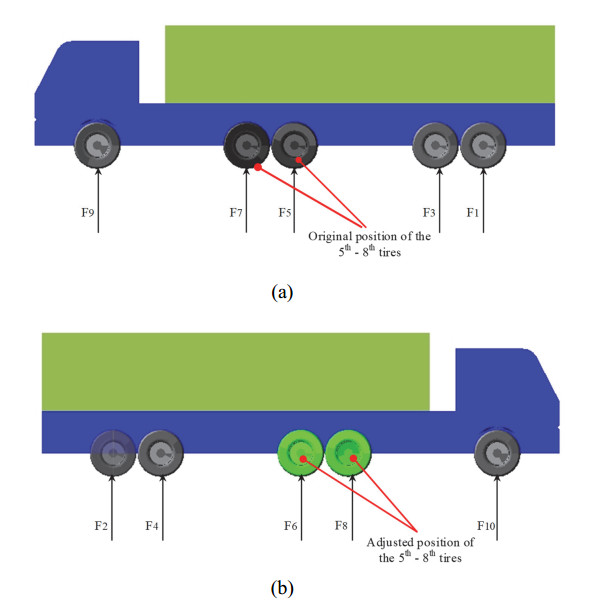
The cartesian coordinate system o-xyz shown in Figure 9 is established. The acceleration of the truck in the y-axis direction is assumed to be zero, that is, the force on the y-axis is in static equilibrium, and the goods loaded by the truck are uniformly distributed in the tail-box, that is, the deviation of the barycenter of the whole truck on the x-axis is zero, and all tires of the truck have the same vertical stiffness. The tires cannot be moved in the direction of the x-axis because of the limitation of the truck structure. Therefore, the same supporting forces of all tires can be achieved by adjusting the tires along the z-axis in accordance with the engineering practice and the relevant theories in section 2.1. The four front wheels of the eight back wheels are regarded as an adjustable unit, known as group A adjustable support unit, and the four rear wheels of the eight back wheels are also regarded as an adjustable unit, known as group B adjustable support unit. With SolidWorks, the barycenter coordinate of the truck is (0 m, –0.418 m, –2.119 m) when the goods are not loaded and (0 m, 0.098 m, –3.254 m) when the goods are loaded. The barycenter is shifted backward, such that the group A adjustable support unit is moved along the negative direction of the z-axis, while the position of the group B adjustable support unit is unchanged. The supporting force of each tire is equal when Eq (19) is met. The original and adjusted positions of each tire in the z-axis direction are shown in Table 1.

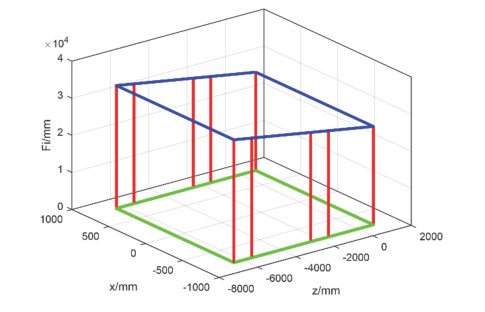
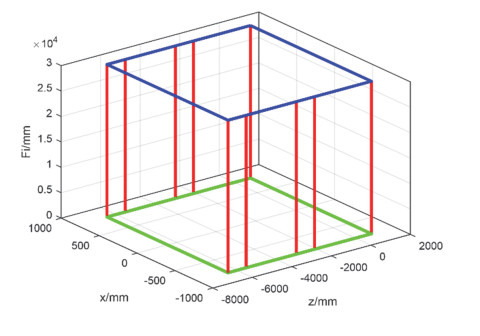
The original and adjusted truck models (Figure 10) are imported from SolidWorks into ADAMS for simulation ^[30,31], and the experimental results of simulation are shown in Figures 11 and 12. In the established Cartesian coordinate system o-zxF_i, the original and adjusted spatial FDPs composed of the position of each tire in the o-zx plane and supporting force of the each tire as coordinate points are shown in Figures 13 and 14. As shown in Figures 13 and 14, the supporting force of the truck tires is distributed in a parallelogram in space before the adjustment, whereas the supporting force of the truck tires is distributed in a rectangular parallel to the o-zx plane in space after the adjustment.

3.2.   Application of layout reconfiguration methods for uniform force characteristics of the support structure of a truck under rectangular constraint surface

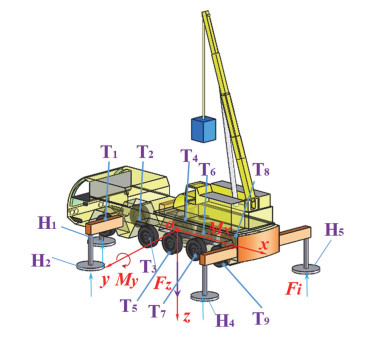
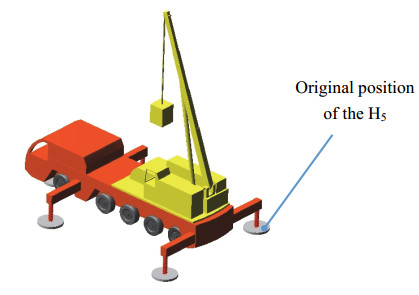
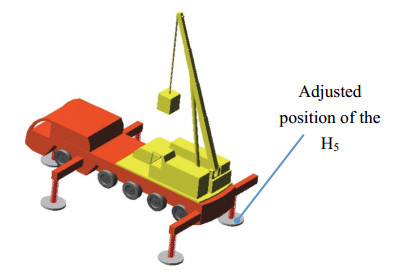
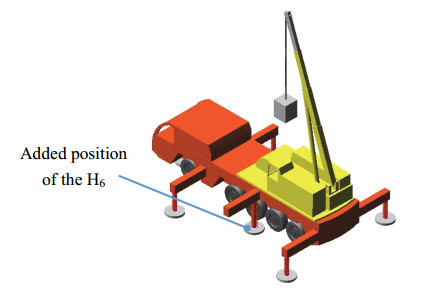
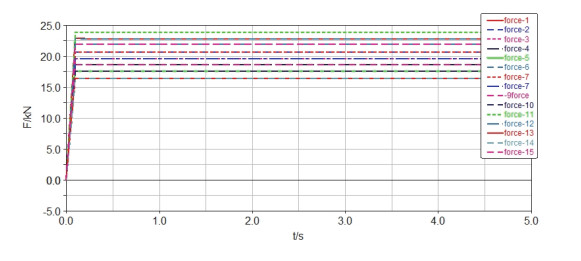
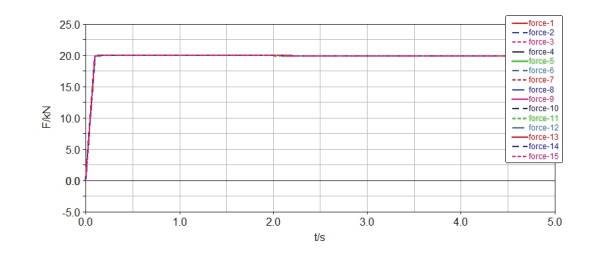
Given the forces on the crane (Figure 15), the external loads F_z, M_x, and M_y acting on the crane are assumed to be 300, −30, and 30 KN·m, respectively, and the jacks and the tires of the crane have the same vertical stiffness. The adjusted layout position of the jacks and tires can be obtained using the displacement reconfiguration method in section 2.3.3, which is listed in Table 2 together with the original position. The number of corresponding jacks and tires in Table 2 is shown in Figure 15. The adjusted layout position of jacks and tires can also be obtained according to the reconfiguration method combined by number and displacement in section 2.3.3, which is listed in Table 3 together with the original position.

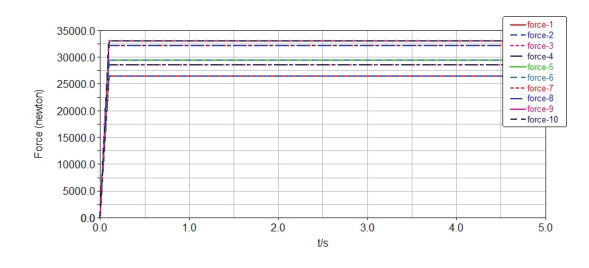
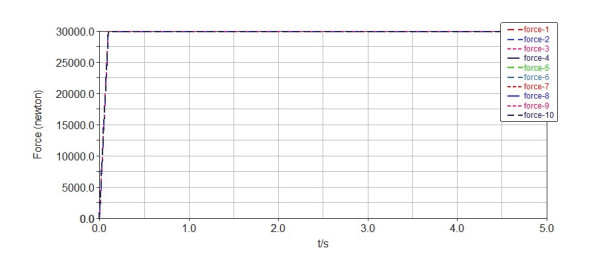
As shown in Figures 16–18, the original and adjusted virtual prototype models of the crane established in SolidWorks are imported into ADAMS for simulation, and the specific simulation results of the original and adjusted supporting forces of five jacks and ten tires are obtained (Figures 19–21, respectively). Simulation results show that all jacks and tires do not have the same supporting force before the layout adjustment but obtain the same supporting force of 20 or 18.75 KN after the later adjustment.

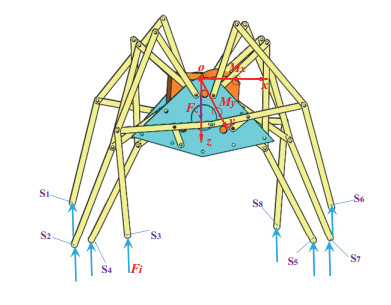
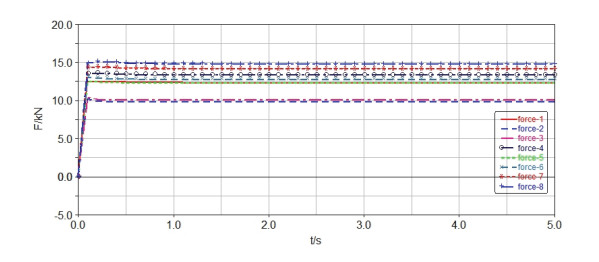
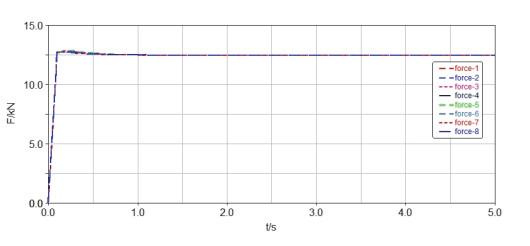
3.3.   Application of layout reconfiguration methods for uniform force characteristics of the support structure of eight-legged spider robot under unconstrained surface

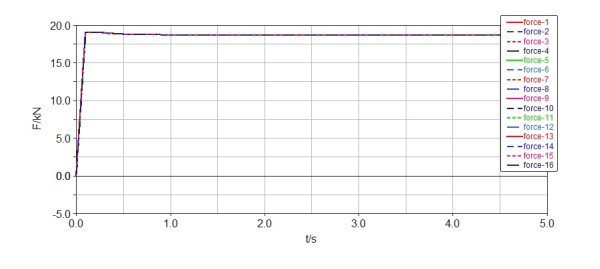
The forces on the eight-legged spider robot are shown in Figure 22. The external loads F_z, M_x, and M_y acting on the eight-legged spider robot are assumed to be 100, 50, and 20 KN·m, respectively. The adjusted layout position of the fulcrum can be obtained using the displacement reconfiguration method in section 2.3.3. The results together with the original position are listed in Table 4. The number of corresponding fulcrums in Table 4 is shown in Figure 22. As listed in Table 4, selecting the position of the fourth fulcrum for adjustment not only achieves the uniform force characteristics of the structure but also avoids mutual interference of the supporting structure during adjustment. If the position of the fifth fulcrum is selected for adjustment, the coordinate of the adjusted position is (3.6, –1) according to the calculation of Eq (19), and interference occurs between this position and the position of the seventh fulcrum (4, –1). Selecting the position of one fulcrum for adjustment in practical engineering is theoretically feasible, but the interference effect of the supporting structure size and spatial position on the adjustment should also be considered.

The original and adjusted virtual prototype models of the crane established in SolidWorks are imported into ADAMS for simulation, and the specific simulation results of the original and adjusted supporting forces provided by eight fulcrums are obtained (Figures 23 and 24, respectively). Simulation results show that all fulcrums do not have the same supporting force before the layout adjustment but obtain the same supporting force of 12.5 KN after the adjustment.

4.   Conclusion

A model of the optimal force transmission of the multiple-fulcrum supporting platform and a model of the force transmission characteristics of the multiple-fulcrum supporting platform with rectangular and circular constrained surfaces are established, and the relationship between the two is demonstrated. Based on the above two models, layout reconfiguration methods for the uniform force characteristics of fulcrums under rectangular and circular constrained surfaces and unconstrained surfaces are proposed. Then, the application of these layout reconfiguration methods in practical engineering is discussed in detail. After studying the force transmission of the multiple-fulcrum supporting platform in the above aspects, the following conclusions can be drawn:

(1) In a multiple fulcrum supporting platform, no matter what the structural form of the support, as long as the stiffness of all supports in the vertical direction is equal, and when the LCP coincides with the FEP by adjusting the position of the fulcrum, the supporting force of all fulcrums in the multiple-fulcrum supporting platform becomes equal.

(2) The FDPs of the multiple-fulcrum supporting platform with rectangular and circular constrained surfaces are parallelograms and ellipses, respectively. If and only if the LCP coincides with the FEP, the FDPs of the multiple-fulcrum supporting platform with rectangular and circular constraint surfaces become rectangular and circular, respectively.

(3) For the multiple-fulcrum supporting platform with rectangular and circular constrained surfaces, only the position of the two fulcrums needs to be adjusted to achieve the uniform force characteristics of the fulcrum. For the multiple-fulcrum supporting platform with unconstrained surfaces, only the position of one fulcrum needs to be adjusted to achieve the uniform force characteristics of the fulcrum.

(4) With the layout reconfiguration methods, the uniform force characteristics of the fulcrum can be efficiently and quickly realized by selecting the fulcrum near the layout reconfiguration axis obtained by clockwise rotating 90° along the direction of external combined resistance moment M for layout adjustment.

Acknowledgments

This research is supported by the Key Laboratory of Road Construction Technology and Equipment (Chang'an University; No. 300102259509), Hunan Province Education Department Key Research Project (No. 18A181) and Hunan Provincial Natural Science Foundation China (No. 2018JJ2122). All authors thank the anonymous reviewers for constructive comments that helped improve this manuscript.

Conflict of interest

There is no conflict of interest for all the authors in this article.