A numerical approach to approximate the solution of a quasilinear singularly perturbed parabolic convection diffusion problem having a non-smooth source term

1.   Introduction

This work focuses on a quasilinear singularly perturbed convection diffusion parabolic initial-boundary value problem, where the source term exhibits a spatial discontinuity. The nonlinear convection coefficient, which characterizes the problem as quasilinear, is the novel aspect of the paper. Here, the source term has a jump discontinuity in space resulting in a weak interior layer appearing near the discontinuity, in addition to the presence of a boundary layer. The aim of this study is to propose a robust $\varepsilon$-uniform method, achieved by discretizing the spatial variable using the standard upwind scheme on a piecewise Shishkin mesh and the temporal variable using the backward Euler scheme on a uniform mesh. The choice of the standard upwind scheme is motivated by its computational efficiency and simplicity, making it a suitable baseline solution for future comparisons with more advanced techniques. Problems of this type can be found in ^[1]. For studies on singular perturbation, one can refer to ^[2,3,4,5], in which various numerical and asymptotic methods are discussed. Regarding singularly perturbed problems with discontinuous terms, among all existing studies in the literature, we will refer only to a few related to our problem. The problem in ^[6] is time independent and has a strong interior layer because of the discontinuity in the source term and the convection coefficient. The problem was solved using the standard upwind scheme. In ^[7], a quasilinear convection-diffusion problem with discontinuous data resulting in strong interior layers was considered. Recently, a semilinear reaction-diffusion parabolic system with a discontinuous source term was studied in ^[8], while a system of quasilinear convection-diffusion problems with discontinuities in both the source term and the convection coefficient was investigated in ^[9]. Singularly perturbed problems occur in numerous scientific and engineering fields, including fluid dynamics ^[10,11], chemical kinetics, population dynamics, control theory ^[12], and semiconductor modeling ^[13,14].

Model problem

Let us first introduce some important notations:

A function $u(s, t)$ is said to be Hölder continuous of order $\lambda$ on $\Omega, \; \text{with} \; \lambda\in (0, 1],$ if and only if $u\in C^0(\Omega)$ and

is finite. This is denoted as $u\in C^{\lambda}(\Omega)$ (for more details, one can refer to ^[15]). For every integer $n\ge0,$

Now, consider the following quasilinear singularly perturbed parabolic initial-boundary value problem where $z\in C^{1+\lambda}(\mathbb{D})\cap C^{2+\lambda}(\mathbb{D}^-\cup\mathbb{D}^+)$:

subject to the boundary and initial conditions

It is assumed that the source term $f(s, t)\in C^{2+\lambda}(\mathbb{D}^-\cup\mathbb{D}^+),$ the convection coefficient $p(s, z)\in C^{2+\lambda}(\bar{\mathbb{D}}),$ and the coefficients $q(s)$, $r(s)\in C^{4+\lambda}\bar{\mathbb{D}}_s$ are smooth functions in their respective domains. The perturbation parameter is assumed to be sufficiently small, such that $0 < \varepsilon < < 1.$ Furthermore, it is assumed that

where $s = \zeta$ is the line of discontinuity, and the source term has a jump discontinuity along $s = \zeta.$ A weak interior layer appears on the right side of the discontinuity, and there is a boundary layer at $s = 0.$ The initial and boundary conditions are assumed to be sufficiently smooth on $\bar{\mathbb{D}}$ and fulfill the compatibility conditions at the two corner points $(0, 0), \; (1, 0)$ as follows:

and

Similarly, compatibility conditions are assumed to be fulfilled at the transition point $(\zeta, 0)$. Under these conditions, problem (1.1)–(1.5) has a unique solution $z\in C^{(1+\lambda)}(\mathbb{D})\cap C^{(2+\lambda)}(\mathbb{D}^-\cap\mathbb{D}^+),$ as explained in ^[15,16,17].

This paper is organized as follows: In section 2, some analytical results are presented. Discretizations of the mesh and the solution are given in Section 3. Section 4 deals with error analysis, and in Section 5, two numerical examples are given to illustrate the performance of the proposed method. Finally, a conclusion of the paper is given in Section 6.

Throughout the paper, $C$ denotes a generic constant that is independent of $\varepsilon$ and the mesh parameters $\mathcal{N}, \; \mathcal{M}$. The maximum pointwise norm is used, denoted as $\|w\|_D = \max_{(s, t)\in D}|w(s, t)|$. When $D = \bar {\mathbb{D}}$, we will simply write $\|w\|,$ avoiding the subscript.

2.   Analytical results

In this section, some theoretical results are presented. Although the proofs of the following results are well known in the literature, we include them here for the sake of clarity and completeness.

Theorem 2.1. (Minimum principle): Let $w \in C^{0}(\bar{\mathbb{D}})\cap C^{2}(\mathbb{D}^-\cup \mathbb{D}^+)$ satisfy

Then, $\; \; \; \; \; \; \; \; \; \; \; \; \; w(s, t) \leq 0\; \; \mathit{\text{for all}} \; (s, t)\in \bar{\mathbb{D}}$.

Proof. Consider a function $\nu,$ such that

where $\alpha\geq\alpha_1\geq\alpha_2.$ Let $(s^*, t^*)$ be any point at which $\nu$ attains its maximum value in $\mathbb{D}.$ If $\nu(s^*, t^*)\le 0,$ then there is nothing to prove. Now, we proceed by contradiction. Consider that $\nu(s^*, t^*) > 0,$ then either $(s^*, t^*)\in (\mathbb{D}^-\cup\mathbb{D}^+)$ or $(s^*, t^*) = (\zeta, t^*).$ If $(s^*, t^*)\in (\mathbb{D}^-\cup\mathbb{D}^+),$ then

Hence,

which is a contradiction.

If $(s^*, t^*) = (\zeta, t^*),$ then $[w_s](\zeta, t^*) = [\nu_s](\zeta, t^*)+\dfrac{\alpha_1-\alpha_2}{2\varepsilon}\nu(\zeta, t)\leq 0,$ which is also a contradiction. This completes the proof. □

Theorem 2.2. Let $z$ be the solution of (1.1)–(1.5). Then, it holds:

and

where the suffix $(\kappa)$ denote the $\kappa^{th}$ derivative of $z$ with respect to $s$.

Proof. Consider the following barrier functions

We note that $\Psi^{\pm}\in C^{0}(\bar{\mathbb{D}})\cap C^{2}(\mathbb{D}^-\cup \mathbb{D}^+),$ and

Consequently, with the help of Theorem 2.1, the required result can be proved. By following a similar procedure as in ^[3], the bounds of the derivatives can be obtained. □

Decomposition of the solution

We decompose the solution as the sum of a regular component $x$ and a singular component $y$ as:

where the regular component $x\in C^0(\mathbb{D})$ satisfies the following problem

and the singular component $y\in C^0(\mathbb{D})$ satisfies

Furthermore, the regular and singular components satisfy the conditions

The regular component $x$ can be further decomposed as

where $x_0, \; x_1, \; x_2\in C^0(\mathbb{D})$ and satisfy the following problems, respectively,

The singular component can be further decomposed as $y = y_1+y_2,$ where $y_1\in C^2(\mathbb{D})$ is the boundary layer function satisfying

and $y_2\in C^0(\mathbb{D})$ is the weak interior layer function, which is the solution of

The method of upper and lower solutions will be useful to prove the existence and uniqueness of the regular component. By reversing all the inequalities, we can obtain the corresponding definition of lower solutions. In what follows, the upper and lower solutions will be denoted by $\Phi$ and $\phi$, respectively.

Definition 2.3. A function $\Phi$ is an upper solution of problem (2.1) if

The solution of (2.1) satisfies Nagumo's condition on $\mathbb{D}^-\cup \mathbb{D}^+$ relative to the pair $\Psi(s, t) = \|f\|+\gamma s, \; \; \gamma: = \sup_{\phi \leq z \leq\Phi} |p(s, z(s, t))|.$ Thus, by using the result from [18, Thm 1.5.1], the existence of the regular component can be ensured by constructing lower and upper solutions. These components satisfy the bounds established in the following results.

Lemma 2.4. For any integers $\kappa, m$ satisfying $0\leq \kappa+m \leq2,$ the solution $x$ of (2.1) satisfies the following bounds:

Proof. Note that $x_0$ and its derivatives are independent of $\varepsilon,$ and

which gives

where $\hat{x}(s, t)$ is such that

Thus, the function $x_1$ satisfies the following problem

Hence, $|x_1|\leq C$ and $\left|\dfrac{\partial x_1}{\partial s}\right|\leq C.$ Differentiating the above equation, we can also get the remaining bounds. Now, from Eqs (2.6) and (2.7), we obtain

Hence, we get

which gives

where $\tilde{x}$ is given by

Hence, we have

Thus, by combining the bound of $x_0, \; x_1,$ and $x_2$, the proof is completed. □

Lemma 2.5. For any integers $\kappa, m,$ the solutions $y_1$ and $y_2$ of problems (2.8) and (2.9), respectively, satisfy the following bounds:

Proof. To find the bounds of $y_1,$ choose $C$ sufficiently large so that

Since $L y_1 = 0,$ and

then by the minimum principle ^[4], we get

Now, taking the stretching variable $\tilde{s} = s/\varepsilon$ and following a procedure similar to that in ^[19], we can easily obtain bounds for the derivatives of $y_1$.

To find the bounds for $y_2,$ we choose suitable barrier functions $\Psi(s, t) = -\psi(s, t) \pm y_2(s, t),$ where

Clearly, $\Psi(0, t) = -\psi(0, t)\le0, \; \Psi(1, t) = -\psi(1, t)\le0, \; \Psi(s, 0) = -\psi(s, 0)\le0.$ Also,

and $\left[\dfrac{\partial \Psi}{\partial s}\right](\zeta, t) = -\left[\dfrac{\partial \psi}{\partial s}\right](\zeta, t)\pm\left[\dfrac{\partial y_2}{\partial s}\right](\zeta, t)\ge0.$ Hence, Theorem 2.1 implies $\Psi(s, t)\leq0,$ for all $(s, t)\in\bar{\mathbb{D}},$ that is,

Hence, with the help of Theorem 2.1, we arrive at the required result.

Now, to get the derivative bounds, we follow a similar procedure as in ^[20]. The result is proven for $\mathbb{D}^-$ and a similar procedure can be adopted for $\mathbb{D}^+.$ Take $\eta = (s-\zeta)/\varepsilon$ and set $\tilde{\mathbb{D}} = (0, \zeta\varepsilon^{-1})\times(0, 1].$ Additionally, let $\tilde{y}_2(\eta, t) = y_2(s, t),$ and similarly define the transformed coefficients $\tilde{p}, \tilde{q}, \tilde{r}.$ Then, Eq (2.9) becomes

For each $\eta\in (0, \zeta\varepsilon^{-1})$ and each $\mu > 0,$ let $R_{\eta, \mu}$ denote the rectangle

and let $\bar{R}_{\eta, \mu}$ denote the closure of $R_{\eta, \mu}$ in the $(\eta, t)-$plane.

Now, since $\tilde{y}_2$ satisfies (2.9) and (2.12), by ^[15], for $0\le \kappa+2m\le4,$

Using bounds for $y_2$, we have

Changing variables, this becomes

□

3.   Discretization of the problem

3.1.   Mesh discretization

Let us subdivide the domain $\bar {\mathbb{D}}_s$ into

where the transition points are defined as

We will divide each of the four intervals in $\mathcal{N}/4$ subintervals. The mesh points are denoted by

Clearly, $\bar{\mathbb{D}}_s ^\mathcal{N} = \{s_i\}_{i = 0}^\mathcal{N}$ where $s_0 = 0, s_{\mathcal{N}/2} = \zeta$ and $s_\mathcal{N} = 1.$ The mesh width will be

Additionally, define ${H}_i = \dfrac{h_i+h_{i+1}}{2}.$

The time variable is discretized using a uniform mesh:

The piecewise uniform mesh is $\mathbb{D}^{\mathcal{N}, \mathcal{M}} = \mathbb{D}_s^\mathcal{N} \times \mathbb{D}_t^\mathcal{M}.$ Let us also define some useful discrete domains $\bar{\mathbb{D}}^{\mathcal{N}, \mathcal{M}} = \bar{\mathbb{D}}_s^\mathcal{N} \times \mathbb{D}_t^\mathcal{M}, \; \; \partial \mathbb{D}^{\mathcal{N}, \mathcal{M}}$ $= \bar{\mathbb{D}}^{\mathcal{N}, \mathcal{M}}\backslash\mathbb{D}^{\mathcal{N}, \mathcal{M}}, \; \; \mathbb{D}^{\mathcal{N}, \mathcal{M}-}$ $= \mathbb{D}_s^{\mathcal{N}-} \times \mathbb{D}_t^\mathcal{M}, \; \mathbb{D}^{\mathcal{N}, \mathcal{M}+} = \mathbb{D}_s^{\mathcal{N}+} \times \mathbb{D}_t^\mathcal{M}.$

3.2.   Discretization of the problem

The forward difference $D_s^+$ and backward difference $D_s^-$ operators in space and the backward difference operator $D_t^-$ in time are given by

A difference operator of second order in space is described as:

Using these operators, we obtain a discretization of problem (1.1)–(1.4) as:

where $Z_i^j$ denotes an approximate value of $z(s_i, t_j)$, $p_i^{j} = p(s_i, Z_i^{j}), \; \; q_i = q(s_i), \; \; r_i = r(s_i), \; \; f_i^j = f(s_i, t_j).$

The finite difference operator $L_{\mathcal{N}}^{\mathcal{M}}$ satisfies the following discrete minimum principle:

Theorem 3.1. (Discrete minimum principle) Let $W$ be a mesh function defined on the discretized domain $\bar{\mathbb{D}}^{\mathcal{N}, \mathcal{M}}.$ If $W\leq0$ on $\partial \mathbb{D}^{\mathcal{N}, \mathcal{M}}, \; L_\mathcal{N}^\mathcal{M}W_i^j\geq 0$ on $\mathbb{D}_s^{\mathcal{N}, }$ and $D^+_sW_{\mathcal{N}/2}^j-D^-_sW_{\mathcal{N}/2}^j\geq0, \; \; \mathit{\text{for}}\; j = 1, 2, ..., \mathcal{M},$ then $W_i^j\leq0$ for all $(s_i, t_j)\in\bar{\mathbb{D}}^{\mathcal{N}, \mathcal{M}}.$

Proof. By following the mehodology in ^[21], we proceed by contradiction. Let us assume that $(s_n, t_m)$ is a point where $W$ attains its maximum. If $W_n^m\le0,$ then there is nothing to prove. Now, suppose that $W_n^m > 0.$ Clearly, $n\neq 0, \mathcal{N},$ and hence, either $s_n\in \mathbb{D}^{\mathcal{N}, -}_s\cup \mathbb{D}^{\mathcal{N}, +}_s$ or $n = \mathcal{N}/2.$ First consider the case $s_n\in \mathbb{D}_s^{\mathcal{N}, -}\cup \mathbb{D}_s^{\mathcal{N}, +}.$ Then, $W_{n}^m-W_{n-1}^{m}\ge0, \; W_{n+1}^m-W_n^{m}\le0$ and $W_{n}^m-W_n^{m-1}\ge0.$ Hence,

which is a contradiction. Now, the only possibility is $n = \mathcal{N}/2,$ and we have

which is again a contradiction. Hence, the proof is completed. □

4.   Error estimate

To get a bound of the nodal error $|(Z- z)(s_i, t_j)|$, we will proceed as follows. First, we define the regular component $X$ and the singular component $Y$ of the discretized solution $Z.$ Later, the nodal errors are considered outside and within the layer using these mesh functions. We assume $\mathcal{M} = C\mathcal{N}$ throughout the rest of the paper.

Define the discrete regular component $X$ to be the solution of the following system:

Define the discrete singular components $Y$ to be the solution of the following system:

where for any mesh function $W,$ the jump discontinuity along the line $s = \zeta$ is represented by:

The singular component can be further decomposed as $Y = Y_1+Y_2$ where $Y_1$ is the boundary layer function satisfying

and $Y_2$ is the weak interior layer function, which solves the problem

So, the discretized solution can be expressed as

Lemma 4.1. The regular component $X$ of the discrete solution satisfies the following $\varepsilon$-uniform error estimate:

Proof. Let us first consider the case $s_i\leq\zeta,$ we have

Introduce the linear difference operator

where $\xi_i^j$ is defined implicitly by

Note that $\|p_z(s, \xi_i^j)\frac{\partial x }{\partial s}\|\le C.$ Now,

Then by using standard local truncation error estimates and by Lemma 2.4, we have

Using the barrier functions $\psi^{\pm}(s, t) = -C\mathcal{N}^{-1}(\zeta-s_i)\pm(X-x)(s_i, t_j)$ and the discrete minimum principle, the proof can be completed in the usual way. A similar procedure can be used for $s_i\ge\zeta$, using a suitable barrier function and Theorem 3.1. □

Lemma 4.2. For $(s_i, t_j)\in \mathbb{D}^{\mathcal{N}, \mathcal{M}},$ the boundary layer function $Y_1$ satisfies

Additionally, for $s_i\geq \theta_1,$ it holds that $|Y_1|\leq C\mathcal{N}^{-1}.$

Proof. Let us first consider the case $s\le \zeta.$ In the case when $\theta_1\le 1/4$ for the region away from the layer $[\theta_1, \zeta],$ using Lemma 2.5, we have

Now, consider the following transformation

where $|\Lambda(s_i, t_j)|\le C$ so that, for sufficiently large $\mathcal{N}\ge \mathcal{N}_0$ ($\mathcal{N}_0$ is independent of $\varepsilon$) and for sufficiently small $\varepsilon\le \varepsilon_0$ ($\varepsilon_0$ is independent $\mathcal{N}$)

and $\hat{Y_1}(0, t) = |y_1(0, t)|, \; \hat{Y_1}(\zeta, t) = 0.$ Now, we take

where $\xi_2 > \xi_1 > 0$ are suitably chosen constants. Let $\tilde{Y}_1$ be the solution of

Then, using the discrete comparison principle, we have

Hence,

Now, for the layer region $[0, \theta_1],$ we have

Let us define the linear discrete operator

where $\xi_i^j$ is given implicitly by $p_s(s, \xi_i^j)(Y_1-y_1)\equiv p(s, Y_1)-p(s, y_1).$ Proving that

this linear discrete operator satisfies the maximum principle.

Now, adopting the methodology as in ^[3], using a suitable barrier function $\bar{Y}_1,$ which is the solution of the problem:

and a discrete comparison principle, the proof is complete. Similarly, bounds for the case $s > \zeta$ can be proved easily. □

Lemma 4.3. The following $\varepsilon$-uniform bound holds:

Proof. Since

it is enough to prove the bounds for each term in the right side of the equation. Now,

and $\left\|{\dfrac{\partial x}{\partial s}}\right\|_{\mathbb{D}^-}\le C,$ which implies $|D_s^-x(\zeta, t_j)|\le C$ and $|D_s^-(X-x)(\zeta, t_j)| = |(X-x)(\zeta-h_l, t_j)/h_l|\le C\mathcal{N}^{-1}$ by Lemma 4.1. Hence,

Now, when $s_i\ge \zeta$,

and $\left\|{\dfrac{\partial x}{\partial s}}\right\|_{\mathbb{D}^+}\le C.$

Also by applying Lemma 3.14 of ^[3], for $s_i\ge \zeta,$ we get

which gives

Now, to get the bounds for $Y_1,$ note that $Y_1(s_i, t_j)\le C\mathcal{N}^{-1}, \; s_i\ge \theta_1,$ and hence

Finally,

Now, by following the arguments of Lemma 3.14 from ^[3] and using the bounds of the derivatives of $y_1,$ one can get

Hence,

Now, by combining the Eqs (4.6), (4.8), (4.9), and (4.11), the proof is complete. □

Concerning the interior layer function, the same bounds can be obtained, as stated in the following result.

Lemma 4.4. For $(s_i, t_j)\in \mathbb{D}^{\mathcal{N}, \mathcal{M}},$ the interior layer function $Y_2$ satisfies

Proof. Let us first get the error estimates at the line of discontinuity $s = \zeta.$ Recalling that $[x_s(\zeta, t)]+[(y_2)_s(\zeta, t)] = 0$, we obtain

Using [Lemma 3.14, ^[3]], we have

Also, it is

which implies

Finally,

Using inequalities (4.14)–(4.16) and Lemma 3.16 ^[3], we obtain from (4.13)

Consider the following transformation for the outer region $[\theta_1, \zeta],$

where $|\omega(s_i, t_j)|\leq C$ so that for $\mathcal{N}\geq \mathcal{N}_0$ and $\varepsilon\leq \varepsilon_0$ (where $\mathcal{N}_0$ is independent of $\varepsilon$ and $\varepsilon_0$ is independent of $\mathcal{N}$),

By choosing a suitable barrier function $\omega(s_i, t_j)$ given by

with $\hat{\xi}_2 > \hat{\xi}_1 > 0$ appropriate constants, the operator satisfies a comparison principle and we can get that

where $\tilde{Y}_2(s_i, t_j)$ is the solution of the following problem

Hence,

Now, let us consider the truncation error in the layer regions:

where $\bar{\xi}_i^j$ is defined implicitly by

Note that $\|p_z(s, \xi_i^j)\frac{\partial x }{\partial s}\|\le C.$ Now, we define the linear discrete operator

The operator satisfies a discrete comparison principle, providing that the inequality

holds. Now, the operator $\mathcal{L}_{y_2}^{\mathcal{N}, \mathcal{M}}$ follows the linear case as in ^[22]. With the help of a comparison principle and a suitable barrier function $B_{i, j}^{\pm} = C\mathcal{N}^{-1}+C\mathcal{N}^{-1}\ln\mathcal{N}\pm(Y_2-y_2)(s_i, t_j),$ we get the required result, as usually. □

Now, we will state the main theoretical result of this paper.

Theorem 4.5. Let $z$ be the solution of problem (1.1) and $Z$ be the numerical solution of (3.3). Then, the following error estimates hold:

and

Proof. Combining Lemmas 4.1, 4.2, and 4.4, the proof is completed.

To derive the error bound for approximations to the scaled derivative, by applying the arguments from [3, Section 3.5], separately on each subdomain $[0, \zeta]\times(0, T]$ and $[\zeta, 1]\times(0, T],$ we get

and from the proof of Lemma 4.3, we obtain

Now, again by applying the arguments from [3, Section 3.5], for $s_i\ge \zeta,$ we can get the following bounds

For, $s_i < \zeta$, define $\tilde{Y}_2(s_i, t_j) = Y_2(s_i, t_j)-Y_2(\zeta, t_j)$ with

Then, for $s_i < \zeta,$

where $\tilde{y}_2$ is defined analogously to $\tilde{Y}_2.$ Now, by adopting the methodology from ^[3], we can bound the second term $D_s^+(\tilde{Y}_2-\tilde{y}_2)(s_i, t_j)$ on the right side of Eq (4.17), whereas the first term $D_s^+(Y_2-y_2)(\zeta, t_j)$ of Eq (4.17) is already bounded. □

5.   Numerical results

To validate the theoretical results obtained in the previous sections, the proposed scheme has been employed for solving two test problems. In order to get numerical solutions, we have linearized system (3.3) and consider the following system

where we used a linearization technique as the one described in ^[23,24]. The above system can be expressed in matrix form as

where $A$ is the coefficient matrix, which is an M-matrix of order $(\mathcal{N} - 1)\times(\mathcal{N} - 1), \text{and}\; \textbf{Z}^j = \{\mathcal{Z}_1^0, \mathcal{Z}_2^j, ..., \mathcal{Z}_{N-1}^j\}, \; \; j = 1, 2, ..., \mathcal{M}.$

Using $\textbf{Z}^0 = \{\mathcal{Z}_1^0, \mathcal{Z}_2^0, ..., \mathcal{Z}_{N-1}^0\} = \{z_0(s_1), z_0(s_2), ..., z_0(s_{N-1})\}, \; \mathcal{Z}_0^j = z_l(t_j), \; \mathcal{Z}_N^j = z_r(t_j), \; j = 1, 2, ..., \mathcal{M},$ the above system can be solved for $\textbf{Z}^j.$

The double mesh principle ^[3] is applied to approximate the errors in the maximum norm. For simplicity, we take $\mathcal{M} = C\mathcal{N}.$ The errors are obtained through

where $\mathcal{Z}^{\mathcal{N}, \mathcal{M}}$ and $\mathcal{Z}^{2\mathcal{N}, 2\mathcal{M}}$ represent the numerical solutions to problem (1.1) on two meshes with $\mathcal{N}$ and $2\mathcal{N}$ number of subintervals, respectively. The finer mesh has the mesh points of the coarse mesh along with their midpoints. The maximum pointwise error norm is determined by

Furthermore, the approximate orders of convergence are calculated using the standard formula:

The errors and orders of convergence associated with time and space are calculated separately by fixing $\mathcal{N}$ and $\mathcal{M},$ respectively. The errors $E_{\mathcal{N}}, E_{\mathcal{M}}$ and the maximum pointwise error norms $E^{\mathcal{N}}, E^{\mathcal{M}}$ are obtained as

The estimate of orders of convergence for space and time are calculated, respectively, by

Example 5.1. Consider problem (1.1) with the following data

Example 5.2. Consider problem (1.1) with the following data

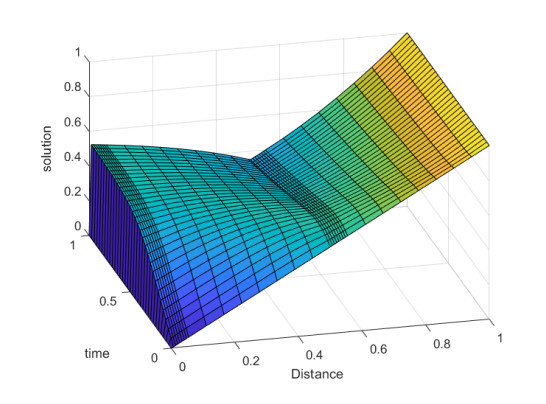
For $\varepsilon = 2^{-7}$ and $\mathcal{N} = 32$, solution graphs are given for both problems. From Figures 1 and 2, one can clearly observe that apart from a boundary layer at $s = 0$, a weak interior layer exists at the right side of the line of discontinuity. For $\varepsilon = 2^{-6}, ..., 2^{-25}$, $\mathcal{N} = 2^5, ..., 2^{10}$, Tables 1 and 2 provide the pointwise errors and convergence rates for Examples 1 and 2 with $\mathcal{N} = \mathcal{M}.$ To analyse the rate of convergence in the space and time variable, Tables 3 and 4 are presented with $\mathcal{N} = 256, \; \mathcal{M} = 2^5, ..., 2^{10}$ and Tables 5 and 6 are presented with $\mathcal{M} = 128, \; \mathcal{N} = 2^5, ..., 2^{10}.$ These tables demonstrate an almost first-order convergence in space and a first-order convergence in time. The numerical results presented in these tables corroborate the theoretical findings and confirm that the method achieves nearly first-order convergence.

6.   Conclusions

A quasilinear one-dimensional parabolic convection-reaction-diffusion problem with a discontinuous source term has been considered. The solution exhibits a boundary layer at $s = 0$ and a weak interior layer to the right of the discontinuity. A numerical method is constructed to solve the problem, yielding an $\varepsilon$-uniform convergent numerical approximation to the solution. The method employs the standard upwind scheme on the spatial domain and the backward upwind scheme on the temporal domain. A Shishkin mesh is used to discretize the space while the time is discretized using a uniform mesh. The scheme achieves nearly first-order convergence in space and first-order convergence in time. Two numerical examples supporting the theoretical results are presented.

Author contributions

Ruby: Conceptualization, Formal analysis, Investigation, Methodology, Writing – original draft. Vembu Shanthi: Conceptualization, Formal analysis, Investigation, Methodology, Supervision, Writing – review & editing. Higinio Ramos: Conceptualization, Formal analysis, Investigation, Methodology, Supervision, Writing – review & editing. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

The first author is grateful for financial support in the form of research fellowship(File no. 09/0895(12534)/2021-EMR-I) the Council of Scientific and Industrial Research (CSIR), India.

Conflict of interest

Prof. Higinio Ramos is a Guest Editor of special issue "Numerical Analysis of Differential Equations with Real-world Applications" for AIMS Mathematics. Prof. Higinio Ramos was not involved in the editorial review and the decision to publish this article.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.