A modified projection and contraction method for solving a variational inequality problem in Hilbert spaces

1.   Introduction

Let $H$ be a real Hilbert space, $C$ be a nonempty, closed, and convex subset of $H$, and $F: H\rightarrow H$ be a nonlinear mapping. The variational inequality problem (VIP in short) is to find a point $x^*\in C$ such that

Denote the set of the solutions of VIP (1.1) by $S$. VIP has many applications in economics, optimization, mechanics, and so on; see ^[1,2].

In recent decades, many methods have been proposed for solving the various classes of VIPs. Korpelevich ^[3] proposed the famous extragradient method and proved the weak convergence of the method under certain conditions. It is well known that the extragradient method needs compute two projections on the feasible set $C$ at each iteration, which adds the computation load especially when $C$ has a complex construction. To overcome the drawback, some authors proposed improved methods where only one projection is computed at each iteration, such as Tseng's method ^[4], the subgradient extragradient method ^[5], and the projection and contraction method ^[6]. To the content of this paper, we focus on the projection and contraction method. In ^[6], He proposed a projection and contraction method for solving the monotone VIP (1.1) as follows: $x_0\in H$, and

where $F$ is a monotone and $L$-Lipschitz continuous mapping, $\tau\in\left(0, \frac{1}{L}\right)$, $\gamma\in(0, 2)$ and

The author proved that under certain conditions the sequence $\{x_n\}$ generated by (1.2) converges weakly to a solution of the VIP (1.1).

Since He's result, many modified versions of the projection and contraction method (1.2) have been introduced. For example, Dong et al. ^[7] proposed the following inertial projection and contraction method for solving the monotone VIP (1.1): $x_0\in H$, and

where $F$ is a monotone and $L$-Lipschitz continuous mapping, $\tau\in\left(0, \frac{1}{L}\right)$, $\gamma\in(0, 2)$, $\{\alpha_n\}\subset [0, \alpha]$ with $\alpha < 1$, and

The authors proved that under certain conditions the sequence $\{x_n\}$ generated by (1.4) converges weakly to a solution of the VIP (1.1).

In 2023, Zhang and Chu ^[8] proposed a new extrapolation projection and contraction method by combining the golden ratio technique ^[9] for solving the VIP (1.1) as follows: $x_0, y_1\in H$, and

where $F$ is a pseudomonotone and $L$-Lipschitz continuous mapping, $\mu\in(0, 1)$, $\phi\in(1, \infty)$, $\gamma\in(0, 2)$,

with

and

where $\{\xi_n\}\subset[1, \infty)$ with $\sum_{n = 1}^\infty(\xi_n-1) < \infty$ and $\{\tau_n\}\subset(0, \infty)$ with $\sum_{n = 1}^\infty\tau_n < \infty$. The authors proved that under certain conditions, the sequence $\{x_n\}$ generated by (1.6) converges weakly to a solution of the VIP (1.1). Note the sequence $\{\lambda_n\}$ in (1.8) is permitted to be increasing. The similar definition with $\lambda_n$ in (1.8) can be found in ^[10,11].

On the more projection and contraction methods and golden ratio methods for solving VIPs, the interested readers may refer to ^[12,13,14].

In (1.3), (1.5), and (1.7), the sequence $\{\beta_n\}$ is computed in a self-adaptive manner involving $d(\cdot, \cdot)$ and the constant $\gamma$ is chosen from (0, 2). In fact, besides the projection and contraction methods mentioned above, in almost all versions of projection and contraction methods, the sequence $\{\beta_n\}$ is computed in a similar self-adaptive manner. A natural question is if the range of $\gamma$ can be relaxed or omitted and $\{\beta_n\}$ can be computed by other mains or is replaced by a sequence of numbers that is given in advance at the initial part of the proposed method. It seems that no authors consider the question. In addition, find that $y_n$ in (1.6) can be written as $y_n = \left(1-\frac{1}{\phi}\right)x_n+\frac{1}{\phi}y_{n-1}$, which is a convex combination of $x_n$ and $y_{n-1}$. Replacing $\phi$ with a sequence $\{\phi_n\}$ in $(1, \infty)$, $y_n$ will be $\left(1-\frac{1}{\phi_n}\right)x_n+\frac{1}{\phi_n}y_{n-1}$. In this case, if $\phi_n = \phi$, then $y_n$ is reduced to $y_n$ in (1.6) and so such that $y_n$ in (1.6) is the special case. Based on the above idea, in this paper, we propose a modified version of the method (1.6) where the constant $\gamma$ is omitted and the sequence $\{\beta_n\}$ replaced by a sequence of numbers in (0, 1). The main difference of our method with (1.6) is as follows:

(1) the constant $\phi$ in (1.6) is replaced by a sequence $\{\phi_n\}$;

(2) the constant $\gamma$ in (0, 2) is not needed, and the sequence $\{\beta_n\}$ in (1.7) is replaced by a sequence of numbers in (0, 1), which is the main novelty of our method.

We prove that under certain conditions the proposed method converges strongly to a solution of the VIP (1.1). The numerical examples are presented to illustrate the effectiveness of our method. Although our method is a slight modification of the method (1.6), the numerical results show that our method has a faster convergence rate than the method (1.6) and other related methods.

2.   Preliminaries

In this section, let $H$ be a real Hilbert space and $C$ be a nonempty, closed and convex subset of $H$. Denote the weak convergence by the symbol $\rightharpoonup$. For any $x, y \in H$, it holds that

Definition 2.1. ^[15] A mapping $F: H\to H$ is said to be

(i) Pseudomonotone on $C$ if

(ii) Pseudomonotone with respect to a subset $B\subset C$ on $C$ if

(iii) L-Lipschitz continuous on $H$ if there exists a constant $L > 0$ such that

(iv) Sequentially weakly continuous if for each sequence $\{x_n\}$, one has

Let $C$ be a nonempty closed convex subset of $H$. For any $x\in H$, there exists a unique $z\in C$ such that

Denote the element $z$ by $P_C(x)$. The mapping $P_C: H\to C$ is called the metric projection from $H$ onto $C$.

Lemma 2.1. ^[15] $P_C$ has the following properties:

Lemma 2.2. ^[16] Assume that $\{a_n\}\subset [0, \infty)$, $\{b_n\}\subset (0, 1)$, and $\{c_n\}\subset (0, \infty)$ satisfy the following

If $\sum_{n = 1}^{\infty}b_n = \infty$ and $\limsup_{n\to \infty} \frac{c_n}{a_n} \le 0$ hold, then $\lim_{n \to +\infty}a_n = 0.$

Lemma 2.3. ^[17] Let $\{a_n\}$ be a sequence of non-negative real numbers such that there exists a subsequence $\{a_{n_j}\}$ of $\{a_n\}$ such that $a_{n_j} < a_{n_j+1}$ for all $j\in \mathbb{N}$. Then there exists a non-decreasing sequence $\{m_k\}$ of $\mathbb{N}$ such that $\lim_{k\to \infty} m_k = \infty$ and the following properties are satisfied by all (sufficiently large) number, $k\in \mathbb{N}$:

3.   Main result

In this section, let $C$ be a nonempty, closed and convex subset of a real Hilbert space $H$ and $F: H\to H$ be a mapping. Considering the following conditions:

(A1) $S\ne \emptyset$.

(A2) $\langle F(y), y-z\rangle\ge0$ for all $z\in S$ and $y\in C$.

(A3) $F$ is $L$-Lipschitz continuous.

(A4) For any sequence $\{u_n\}\subset C$ with $u_n \rightharpoonup u$, it has $\langle F(u), u-y\rangle\le \limsup_{n\to\infty}\langle F(u_n), u_n-y\rangle$ for all $y\in C$.

Remark 3.1. Condition (A2), used for example in ^[18], is weaker than the pseudomonotonicity assumption. In fact, from Conditions (A1) and (A2), it follows that $F$ is pseudomonotone with respect to $S$ on $C$. In addition, it needs to be noted that Condition (A4) is not related to the condition that $F$ is sequentially weakly continuous on $C$.

For solving the VIP (1.1), we propose the projection and contraction method as follows.

Remark 3.2. In Algorithm 3.1, the definition of $w_n$ has the same manner as the ones in ^{[19,20,21,22]}. Clearly, if $\phi_n\equiv \phi$ with $\phi > 1$, then $y_n$ is reduced to the one in (1.4). In particular, if $\phi_n = \frac{1+\sqrt{5}}{2}$, then $\phi_n$ is the golden ratio. In the existing projection and contraction methods, $\{\beta_n\}$ is computed in a self-adaptive manner like (1.3), (1.5), and (1.7) and its value strictly depends on the result, which is computed by the self-adaptive formula. However, in our method, $\{\beta_n\}$ is a sequence of numbers in (0, 1) given in advance. Since there is no other restriction imposed on $\{\beta_n\}$, we have the greater freedom to choose or adjust $\{\beta_n\}$ in advance. It is the main difference of our method with the existing projection and contraction methods.

The following remark shows that the stopping criterion in Step 2 can work well.

Remark 3.3. By the definition of $\bar{y}_n$ and Lemma 2.1, we have

If $\bar{y}_n = w_n$ for some $n\in\mathbb{N}$, then it has

Since $\lambda_n > 0$, we have

It follows that $\bar{y}_n\in S$. In addition, it is clear that $F(\bar{y}_n) = 0$ leads to $\bar{y}_n\in S$.

In the rest of this section, for showing the convergence of Algorithm 3.1, we assume that $\{x_n\}$, $\{w_n\}$, $\{y_n\}$, and $\{\bar{y}_n\}$ are infinite sequences.

Lemma 3.1. ^[23] Assume that $\rm (A3)$ holds. Then the Armijo-line search rule $(3.1)$ is well defined, and $\min\left\{ \gamma, \frac{\mu\tau}{L}\right\}\le\lambda_n\le \gamma$ for all $n\in\mathbb{N}$.

Lemma 3.2. Assume that $\rm (A1)$–$\rm (A3)$ hold. Then the sequences $\{x_n\}$, $\{y_n\}$, $\{\bar{y}_n\}$ and $\{w_n\}$ are bounded.

Proof. For each $z\in S$ and $n\in\mathbb{N}$, by the definition of $\bar{y}_n$ and Lemma 2.1, it follows that

By (A2) it holds that

which, together with $\lambda_n > 0$, leads to that

Combining (3.2) with (3.3), we have

So

Multiplying $\beta_n$ on both sides of the above inequality, we get

Substituting (3.4) into

we have

Furthermore, by (3.1) we get

On the other hand, by the definition of $y_{n+1}$ we have

Substituting (3.6) into (3.5), we obtain

It follows that

Hence $\{y_n\}$ is bounded. The boundedness of $\{w_n\}$ is from $\|w_n\| = (1-\psi_n)\|y_n\|\le \|y_n\|$, which implies that $\{P_Cw_n\}$ is also bounded. In addition, $\{F(w_n)\}$ is bounded because of (A3). By the definition of $\bar{y}_n$ we have

From Lemma 3.1 it follows that $\{\bar{y}_n\}$ is bounded. Finally, by (3.5) and the boundedness of $\{w_n\}$, we obtain the boundedness of $\{x_n\}$. The proof is complete.

In the following lemma, we denote the set of weak cluster points of $\{w_n\}$ by $\omega_w(w_{n})$.

Lemma 3.3. Assume that $\rm (A1)$–$\rm (A3)$ hold. If $\lim_{n\to\infty}\|w_n-\bar{y}_{n}\| = 0$, then $\omega_w(w_{n})\subset S$.

Proof. Since $\{w_n\}$ is bounded, $\omega_w(w_{n})\ne\emptyset$. Choose $\bar{w}\in \omega_w(w_{n})$ arbitrarily and assume that $w_{n_k}$ is a subsequence of $\{w_n\}$ such that $w_{n_k}\rightharpoonup\bar{w}$ as $k\to\infty$. From $\lim_{k\to\infty}\|w_{n_k}-\bar{y}_{n_k}\| = 0$ it follows that $\bar{y}_{n_k}\rightharpoonup\bar{w}$ and so $\bar{w}\in C$. For each $y\in C$, from Lemma 2.1 and the definition of $\bar{y}_n$ we have

or equivalently,

Taking $\limsup_{k\to\infty}$ in (3.9), by $\lim_{k\to\infty}\|w_{n_k}-\bar{y}_{n_k}\| = 0$ and Lemma 3.1, we get

Since $F$ is Lipschitz continuous and $\lim_{k\to\infty}\|w_{n_k}-\bar{y}_{n_k}\| = 0$, we have

Note that

Taking $\limsup_{k\to\infty}$ in (3.12) and using (3.11) and (A4) we get

which together with $\bar{w}\in C$ and the arbitrariness of $y\in C$ leads to $\bar{w}\in S$. The proof is complete.

In the position we give the main result on Algorithm 3.1 as follows:

Theorem 3.1. Assume that ${\rm(A1)}$–$\rm (A4)$ hold. The sequence $\{x_n\}$ generated by Algorithm $3.1$ converges strongly to $x^* = P_S(0)$.

Proof. For each $n\in\mathbb{N}$, from the definition of $\{w_n\}$ and (2.1) it follows that

Replacing $z$ in (3.5) and (3.7), and using (3.13), we get

It follows that

Next we divide the following two cases to prove $\lim_{n\to\infty}\|y_n-x^*\| = 0$.

Case 1. Suppose there exists $N\in\mathbb{N}$ such that $\{\|y_n-x^*\|^2\}$ is monotonically nonincreasing for all $n > N$. Since $\{w_n\}$ is bounded, there exists a subsequence $\{w_{n_k}\}$ such that $w_{n_k}\rightharpoonup\bar{w}$. Without loss generality we may assume that

Hence $\{\|y_n-x^*\|^2\}$ is convergent. From (3.8) with $z = x^*$ we have

Since $\phi_n\ge \phi > 1$ and $\lim_{n\to\infty}\psi_n = 0$, letting $n\to\infty$ in (3.16), we get

By Lemma 3.3 and (3.17) we have $\bar{w}\in {S}$. From Lemma 2.1 it follows that

which together with (3.15) leads that

By the hypothesis on $\{\phi_n\}$ and $\{\psi_n\}$, we have

Applying Lemma 2.2 with $a_n = \|y_n-x^*\|^2$, $b_n = \psi_n\left(1-\frac{1}{\phi_{n+1}}\right)$ and $c_n = 2\psi_n\left(1-\frac{1}{\phi_{n+1}}\right)\langle-x^*, w_n-x^*\rangle$ to (3.17) and using (3.18) and (3.19), we obtain $\lim_{n\to\infty}\|y_n-x^*\| = 0$.

Case 2. Suppose that there exists a subsequence $\{m_k\}\subset\mathbb{N}$ with $m_k\to\infty$ such that

From Lemma 2.3 it follows that

By replacing $n$ in (3.14) with $m_k$ and using (3.20) we get

which implies that

By a similar process of showing (3.18), we can get

Hence

Combining (3.21) and (3.22), we have

It follows that $\lim_{k\to\infty}{\|y_{k}-x^*\|}^{2} = 0.$ By the above two cases, we obtain $\lim_{n\to\infty}\|y_n-x^*\| = 0$. Since $\lim_{n\to\infty}\psi_n = 0$, one has

Finally, by (3.5) and (3.23) we have

The proof is complete.

4.   Numerical examples

In this section, we provide the numerical examples to test the convergence of Algorithm 3.1 and compare the numerical experimental results with some related methods. The codes are executed in MATLAB 2016a using a PC (Surface Pro 5) with an Intel(R) Core(TM) i5-7300U CPU running at 2.60GHz and 8.00 GB of RAM.

We first present the following example to test the effectiveness of Algorithm 3.1 for solving the non-monotone VIP (1.1).

Example 4.1. ^[24] Let $H = \mathbb{R}^m$, $C = [0, \pi]\times[0, \pi]\times[0, 1]\times\cdots\times [0, 1]$, $F: H\to H$ be a mapping defined by

It follows that $S = \{\bf 0\}$, Conditions (A1)-(A4) hold and $F$ is not pseudomonotone; see ^[24].

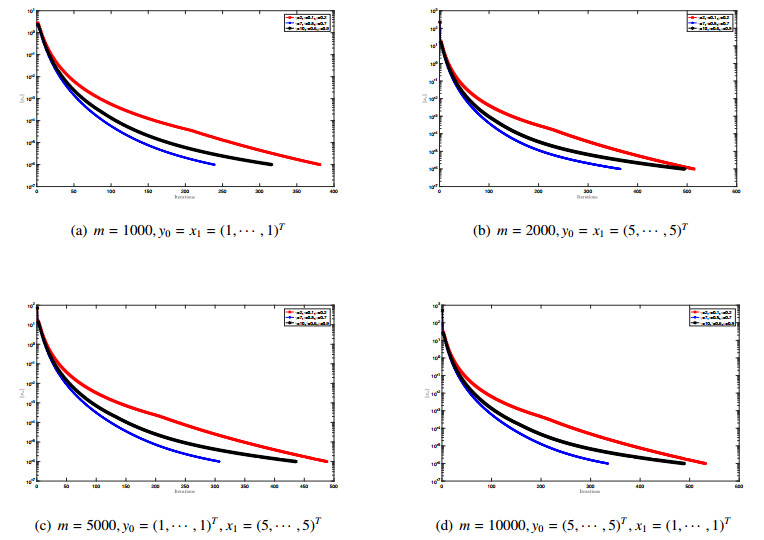
We choose $\phi_n = \frac{1+\sqrt{5}}{2}+\frac{1}{n}$, $\psi_n = \frac{10}{10+n}$, $\beta_n = \frac{110+n}{100+10n)}$ and use $\|x_n\|\le 10^{-6}$ as the stopping criterion of Algorithm 3.1. The computed results for $\{x_n\}$ by Algorithm 3.1 with the different initial points $y_0, x_1$, different dimension $m$, and different parameters $\gamma, \tau$ and $\mu$ are shown in Figure 1. Table 1 gives CPU time (in seconds) of Algorithm 3.1 for this example. From the curves in Figure 1 we see that the sequence $\{x_n\}$ converges to ${\bf0}$.

Next we use the following example to compare the numerical results by our Algorithm 3.1 and the algorithm (1.2) (denoted by Algorithm H), the algorithm (1.6) (denoted by Algorithm Z) and Algorithm 3.1 in ^[13] (denoted by Algorithm T).

Example 4.2. ^[19,25] Let $F: \mathbb{R}^m \to \mathbb{R}^m$ be a mapping defined by $F(x) = Mx+q$ with

where $N$ is an $m\times m$ matrix, $B$ is an $m\times m$ skew-symmetric matrix, and $D$ is an $m\times m$ diagonal matrix with its diagonal entries being nonnegative (hence $M$ is positive semidefinite). The feasible set is

where $E$ is a $k\times m$ matrix and $f\in\mathbb{R}^k$ is a vector. It follows that $F$ is monotone and Lipschitz continuous with the constant $L = \|M\|$. All entries of $N$, $B$ are generated randomly and uniformly in [-2, 2], those of $E$ and $f$ are generated randomly and uniformly in [0, 1], those of $D$ are generated randomly and uniformly in (0, 2). Conditions (A1)–(A4) are satisfied.

We choose the initial points $y_0 = x_{1} = (1, \cdots, 1)^T$ for Algorithm 3.1 and Algorithm Z, and $x_0 = (1, \cdots, 1)^T$ for Algorithm H, and $x_0 = x_{1} = (1, \cdots, 1)^T$ for Algorithm T. The parameters and control sequences for Algorithm 3.1, Algorithm H and Algorithm Z are as follows:

Algorithm 3.1: $\gamma = 2$, $\tau = 0.3$, $\mu = 0.2$, $\psi_n = \frac{100}{100+n}$, $\phi_n = \frac{\sqrt{5}+1}{2}+\frac{1}{n}$, $\beta_n = \frac{1}{10}+\frac{10}{10+n}$;

Algorithm H: $\tau = \frac{7L}{10}$, $\gamma = \frac{3}{2}$;

Algorithm Z: $\phi = \frac{\sqrt{5}+1}{2}$, $\lambda_1 = \frac{1}{20}$, $\gamma = \frac{3}{2}$, $\mu = \frac{3}{5}$, $\xi_n = 1+\frac{1}{n^2}$, $\tau_n = \frac{1}{n^2}$;

Algorithm T: $\phi = 0.6$, $\beta = 0.8$, $\gamma = 2$, $\delta = 0.4$, $l = 0.5$, $\tau = 1.5$, $\epsilon_n = \frac{100}{(1+n)^2}$, $\xi_n = \frac{1}{1+n}$, $\sigma_n = 0.5*(1-\xi_n)$.

We consider the following two cases for this example.

Case 1 $q = {\bf 0}$. In this case, $S = \{{\bf 0}\}$. We use $\|x_n\| < 10^{-3}$ or the maximum number of iterations $n = 1000$ as the common stopping criterion of these algorithms. The numerical results computed are shown in Figure 2 and CPU time (in seconds) is given in Table 2.

Case 2. All entries of $q$ are generated randomly and uniformly in (0, 2). In this case the solution of VIP (1.1) is not known. We use $\|x_n-x_{n-1}\| < 10^{-3}$ as the common stopping criterion of these algorithms. The numerical results computed are shown in Figure 3 and CPU time (in seconds) is given in Table 3.

From Figures 2 and 3, Tables 2 and 3, we see that our Algorithm 3.1 needs the lesser iteration numbers and CPU time than the other three algorithms, which shows that our method has the obvious competitive advantage compared with the algorithms for this numerical example.

5.   Conclusions

In this paper, we proposed a modified projection and contraction method for solving a nonmonotone variational inequality problem in a Hilbert space. Without prior knowledge of the Lipschitz constant of the mapping, we use a line search rule to update the step-size in our algorithm. The main novelty of our method lies in that we use a sequence of numbers in (0, 1) to replace the sequence $\{\beta_n\}$, which is computed in a self-adaptive manner involving $d(\cdot, \cdot)$ in other projection and contraction methods. Under certain conditions, we prove the strong convergence of the proposed method. The numerical examples are given to illustrate the effectiveness of our method. The numerical results show that our method has the obvious competitive advantage compared with the other related algorithms.

Author contributions

Limei Xue : Methodology, computing numerical examples, writing-original draft; Jianmin Song: Formal analysis, writing-original draft; Shenghua Wang: Design of algorithm, proof of conclusions. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

All authors declare no conflicts of interest in this paper.