Modeling hepatitis B transmission dynamics with spatial diffusion and disability potential in the chronic stage

1.   Introduction

In biology, discrete models of interspecific relationships in populations without generation-level overlap are more generalizable than continuous ones, which has attracted many scholars in recent years (see ^{[1,2,3,4,5,6,7,8,9,10,11,12]}). Obviously, all these works indicate that discrete systems have more complex dynamic behavior. The predator-prey model is a class of classical biomathematical model that has been studied by different scholars in terms of the evolutionary patterns of populations over time ^[13,14] and the effects of different functional responses on the stability of populations ^[15,16].

For the predator-prey system, external factors such as food supply, climate change and population migration can affect predation and population reproduction ^[17,18]. However, the effects of changes in predators themselves are often overlooked, such as predator fear ^[19]. Frightened predators tend to eat less, which leads to reduced birth rates and increased mortality ^[19]. Therefore, predator fear, which cannot be quantitatively described, is more difficult to study.

Sasmal ^[20] studied a predator-prey model with Allee effect and reduced reproduction of prey due to cost of fear. They discussed the effects of time scale separation between prey and predator.

where $u$ and $v$ are the prey and predator population densities, respectively. $r$ is the maximum growth rate of the population, $k$ is the carrying capacity, and $\theta$ represents the Allee threshold $(0 < \theta < k)$, below which the population becomes extinct. $f$ refers to the level of fear, which is due to the anti-predator response of prey. $a$ is the predation rate, $\alpha$ is the conversion efficiency of predator by consuming prey, and $m$ represents the predator's natural mortality rate.

To simplify parameters, define $N = \frac{u}{k}, \ P = \frac{a}{rk}v, \ \epsilon = \frac{a\alpha}{r}, \ \theta = \frac{\theta}{k}, \ m = \frac{m}{a\alpha k}, \ f = \frac{rkf}{a}, \ t = a\alpha kt$. Then, the system is given by

At present, there are some studies on predator-prey systems with Flip bifurcation and Hopf bifurcation ^[21] in continuous models, where, however, the chaotic properties have not been mentioned. For example, Khan studied a discrete-time Nicholson-Bailey host-parasitoid model and obtained the local dynamics and supercritical Neimark-Sacker bifurcation in 2017 ^[22]. In 2019, Li et al. investigated the discrete time predator-prey model undergoing Flip and Neimark Sacker bifurcation using the center manifold theorem and bifurcation theory ^[23]. In 2022, Yu et al. gave a description of the bifurcations in theory for a symmetrically coupled period-doubling system, including the Transcritical bifurcation, Pitchfork bifurcation, Flip bifurcation and Neimark-Sacker bifurcation ^[24]. In 2022, Chen et al. studied a discrete predator-prey system with Allee effect, which undergoes Fold bifurcation and Flip bifurcation. They obtained cascades of period-doubling bifurcation in orbits of period-2, 4, 8 and chaotic properties ^[25].

Based on the above analysis and discussion, we obtain the following discrete-time model:

where $h > 0$ refers to the step length of (1.2), $0 < \theta < 1$.

In this paper, we study the existence and stability of four equilibria of model (1.2) and focus on local dynamics of the unique positive equilibrium point in Section 2. In Sections 3 and 4, we study Flip bifurcation and Hopf bifurcation when bifurcation parameter $h$ varies in a small neighborhood of the unique positive equilibrium point. In Section 5, we study chaos scenarios of Flip bifurcation. Meanwhile, some numerical simulations about bifurcations are given by maximum Lyapunov exponent and phase diagrams to verify our results. Finally, brief conclusions are given in Section 6.

2.   Existence and stability of equilibria

Initially, the existence and stability of the equilibrium point of model (1.2) are analyzed.

By calculating model (1.2), obviously, the trivial equilibrium point $E_1 = \left(0, 0 \right)$ and boundary equilibria $E_2 = \left(1, 0 \right)$, $E_3 = \left(\theta, 0 \right)$ are obtained. Since the negative equilibrium point has no practical meaning in biology, the unique positive internal equilibrium point $E_4 = \left(m, \frac{-1+\sqrt{1+4f\left(1-m \right) \left(m-\theta \right)}}{2f} \right)$ is chosen.

The Jacobi matrix of the linear system of (1.2) at any equilibrium point $\left(N^*, P^* \right)$ is given by:

Now, we give some dynamical properties of four equilibria.

Theorem 2.1. For the trivial equilibrium $E_1$, with eigenvalues $\lambda _1 = 1-\frac{h\theta}{\epsilon}$ and $\lambda _2 = 1-hm$.

$(i)$ $E_1$ is a sink if $0 < h < \min \left\{ \frac{2\epsilon}{\theta}, \frac{2}{m} \right\}$, with eigenvalues $\left| \lambda _1 \right| < 1$ and $\left| \lambda _2 \right| < 1$.

$(ii)$ $E_1$ is a source if $h > \max \left\{ \frac{2\epsilon}{\theta}, \frac{2}{m} \right\}$, with eigenvalues $\left| \lambda _1 \right| > 1$ and $\left| \lambda _2 \right| > 1$.

$(iii)$ $E_1$ is a saddle point if $\frac{2\epsilon}{\theta} < h < \frac{2}{m}$ with eigenvalues $\left| \lambda _1 \right| > 1$ and $\left| \lambda _2 \right| < 1$, or $\frac{2}{m} < h < \frac{2\epsilon}{\theta}$ with eigenvalues $\left| \lambda _1 \right| < 1$ and $\left| \lambda _2 \right| > 1$.

$(iv)$ Flip bifurcation occurs at $E_1$ if $h = \frac{2\epsilon}{\theta} < \frac{2}{m}$, with eigenvalues $\lambda _1 = -1$ and $\left| \lambda _2 \right| < 1$, or $h = \frac{2}{m} < \frac{2\epsilon}{\theta}$, with eigenvalues $\lambda _2 = -1$ and $\left| \lambda _1 \right| < 1$.

Theorem 2.2. For the boundary equilibrium $E_2$, with eigenvalues $\lambda _1 = 1+\frac{h}{\epsilon}\left(\theta -1 \right)$ and $\lambda _2 = 1+h\left(1-m \right)$.

$(i)$ $E_2$ is a sink if ${\left\{ \begin{array}{l} \!\!m > 1\\ \!\!0 < h < \min \left(\frac{2\epsilon}{1-\theta}, \frac{2}{m-1} \right)\\ \end{array} \right.\!}$, with eigenvalues $\left| \lambda _1 \right| < 1$ and $\left| \lambda _2 \right| < 1$.

$(ii)$ $E_2$ is a source if ${\left\{ \begin{array}{l} \!\!m < 1\\ \!\!h > \frac{2\epsilon}{1-\theta}\\ \end{array} \right.}$ or ${\left\{ \begin{array}{l} \!\!m > 1\\ \!\!h > \max \left\{\frac{2\epsilon}{1-\theta}, \frac{2}{m-1}\right\}\\ \end{array} \right.\!}$, with eigenvalues $\left| \lambda _1 \right| > 1$ and $\left| \lambda _2 \right| > 1$.

$(iii)$ $E_2$ is a saddle point if ${\left\{ \begin{array}{l} \!\!m > 1\\ \!\!\frac{2\epsilon}{1-\theta} < h < \frac{2}{m-1}\\ \end{array} \right.}$ or ${\left\{ \begin{array}{l} \!\!m > 1\\ \!\!\frac{2}{m-1} < h < \frac{2\epsilon}{1-\theta}\\ \end{array} \right.}$ with eigenvalues $\left| \lambda _1 \right| > 1$ and $\left| \lambda _2 \right| < 1$, or ${\left\{ \begin{array}{l} \!\!m < 1\\ \!\!h < \frac{2\epsilon}{1-\theta}\\ \end{array} \right.}$ with eigenvalues $\left| \lambda _1 \right| < 1$ and $\left| \lambda _2 \right| > 1$.

$(iv)$ Flip bifurcation occurs at $E_2$ if ${\left\{ \begin{array}{l} \!\!m > 1\\ \!\!h = \frac{2\epsilon}{1-\theta} < \frac{2}{m-1}\\ \end{array} \right.}$ with eigenvalues $\lambda _1 = -1$ and $\left| \lambda _2 \right| < 1$, or ${h = \frac{2}{m-1} < \frac{2\epsilon}{1-\theta}}$ with eigenvalues $\lambda _2 = -1$ and $\left| \lambda _1 \right| < 1$.

$(v)$ Transcritical bifurcation occurs at $E_2$ if ${\left\{ \begin{array}{l} \!\!m = 1\\ \!\!h < \frac{2\epsilon}{1-\theta}\\ \end{array} \right.}$, with eigenvalues $\lambda _2 = 1$ and $\left| \lambda _1 \right| < 1$.

Theorem 2.3. For the equilibrium $E_3$, with eigenvalues $\lambda _1 = 1+\frac{h}{\epsilon}\theta \left(1-\theta \right)$ and $\lambda _2 = 1+h\left(\theta -m \right)$.

$(i)$ $E_3$ is a source if $\theta > m$ or ${\left\{ \begin{array}{l} \!\!\theta < m\\ \!\!h > \frac{2}{m-\theta}\\ \end{array} \right.}$, with eigenvalues $\left| \lambda _1 \right| > 1$ and $\left| \lambda _2 \right| > 1$.

$(ii)$ $E_3$ is a saddle point if ${\left\{ \begin{array}{l} \!\!\theta < m\\ \!\!0 < h < \frac{2}{m-\theta}\\ \end{array} \right.}$, with eigenvalues $\left| \lambda _1 \right| > 1$ and $\left| \lambda _2 \right| < 1$.

There is no situation as $\left| \lambda _1 \right| < 1$, $i.e.,$ stability does not exist.

Theorem 2.4. For the internal equilibrium $E_4$,

$(i)$ $E_4$ is a sink if

$(ii)$ Transcritical bifurcation occurs at $E_4$ if

$(iii)$ Flip bifurcation occurs at $E_4$ if

$(iv)$ Hopf bifurcation occurs at $E_4$ if

Proof. The Jacobi matrix of (1.2) at point $E_4 = \left(N_0, P_0 \right)$ is

where $n = 1+\sqrt{1+4f\left(1-m \right) \left(m-\theta \right)}$.

Meanwhile, the characteristic polynomial of $J\!\mid_{\left(N_0, P_0 \right)}^{}$ is given by:

where

Then, eigenvalues of $J\!\mid_{\left(N_0, P_0 \right)}^{}$ are $\lambda _1 = \frac{A+1+\sqrt{\varDelta}}{2}$ and $\lambda _2 = \frac{A+1-\sqrt{\varDelta}}{2}$, where $\varDelta = (A-1)^2-4BC$.

$(i)$ $\left(N_0, P_0 \right)$ is a sink, if $\left| \lambda _1 \right| < 1$ and $\left| \lambda _2 \right| < 1$. From the Jury Criterion ^[26], we obtain ${\left\{ \begin{array}{l} \!\!1+\left(A+1 \right) +\left(A+BC \right) > 0\\ \!\!1-\left(A+1 \right) +\left(A+BC \right) > 0\\ \!\!1-\left(A+BC \right) > 0\\ \end{array} \right.}$.

$(ii)$ If $\varDelta > 0$, $\lambda _1 = 1$ and $\left| \lambda _2 \right| < 1$ or $\lambda _2 = 1$ and $\left| \lambda _1 \right| < 1$, then we have ${\left\{ \begin{array}{l} \!\!BC = 0\\ \!\!\left| A \right| < 1\\ \end{array} \right.}$.

$(iii)$ If $\varDelta > 0$, $\lambda _1 = -1$ and $\left| \lambda _2 \right| < 1$ or $\lambda _2 = -1$ and $\left| \lambda _1 \right| < 1$, then we have ${\left\{ \begin{array}{l} \!\!2A+BC+2 = 0\\ \!\!\left| A+2 \right| < 1\\ \end{array} \right.}$.

$(iv)$ If $\varDelta < 0$, $\left| \lambda _1 \right| = \left| \lambda _2 \right| = 1$, which is a pair of conjugate complex roots, then we have ${\left\{ \begin{array}{l} \!\!A+BC = 1\\ \!\!0 < \left| A+1 \right| < 2\\ \end{array} \right.}$.

When $\lambda_1$ and $\lambda_2$ is a pair of conjugate complex roots, we assume $\lambda _1 = a+bi$ and $\lambda _2 = a-bi$ $\left(a^2+b^2 = 1\, \ b\ne 0 \right)$, $i.e.$, $0 < \left| a \right| < 1$. Since $\left(\lambda -\lambda _1 \right) \left(\lambda -\lambda _2 \right) = \lambda ^2-\left(\lambda _1+\lambda _2 \right) \lambda +\lambda _1\lambda _2 = 0$, obviously we have $\lambda _1+\lambda _2 = A+1 = 2a$ and $\lambda _1\lambda _2 = A+BC = 1$.

All of the expressions $A, B, C$ can be brought into equations mentioned above to obtain the corresponding conclusions.

3.   Flip bifurcation at $E_4$

In this section, we discuss how system (1.2) undergoes Flip bifurcation around its internal equilibrium $E_4 = \left(m, \frac{-1+\sqrt{1+4f\left(1-m \right)\left(m-\theta \right)}}{2f} \right)$ when $h$ is chosen as bifurcation parameter. The necessary conditions for Flip bifurcation to occur is given by the following curve:

where $D = \frac{h}{\epsilon}\left(\frac{m\left(1+\theta -2m \right)}{1+\sqrt{1+4f\left(1-m \right) \left(m-\theta \right)}} \right) +3$ and $n = 1+\sqrt{1+4f\left(1-m \right) \left(m-\theta \right)}$.

3.1.   Existence condition of Flip bifurcation at $E_4$

The Jacobi matrix of the linear system of (1.2) at the equilibrium point $\left(N_0, P_0 \right)$ is given by:

where $n = 1+\sqrt{1+4f\left(1-m \right) \left(m-\theta \right)}$.

In order to obtain the bifurcation properties, we consider translations $\overline{N_{n+1}} = N_{n+1}-N_0$, $\overline{P_{n+1}} = P_{n+1}-P_0$ for shifting $\left(N_0, P_0 \right)$ to the origin. Then, the model (1.2) is given by

Using Taylor expansion at the point $E_4\left(N_0, P_0 \right)$ yields the following expression :

where

$\psi _1\left(\overline{N_n}, \overline{P_n} \right) = b_1\overline{N_n}^2+b_2\overline{N_n}\overline{P_n}+b_3\overline{P_n}^2+b_4\overline{N_n}^3+b_5\overline{N_n}^2\overline{P_n}+b_6\overline{N_n}\, \overline{P_n}^2+b_7\overline{P_n}^3+O\left(\left(\left| \overline{N_n} \right|+\left| \overline{P_n} \right| \right)^4 \right)$,

$\psi _2\left(\overline{N_n}, \overline{P_n} \right) = \overline{N_n}\, \overline{P_n}$,

$b_1 = \frac{-3N_0+1+\theta}{1+fP_0}$, $b_2 = \frac{\left[ 3N_0^2-2\left(1+\theta \right) N_0+\theta \right] f}{\left(1+fP_0 \right) ^2}-1$, $b_3 = \frac{\left[ -N_0^3+\left(1+\theta \right) N_0^2-\theta N_0 \right] f^2}{\left(1+fP_0 \right) ^3}$, $b_4 = \frac{-1}{1+fP_0}$, $b_5 = \frac{\left(3N_0-1-\theta \right) f}{\left(1+fP_0 \right) ^2}$,

$b_6 = \frac{\left[ 3N_{0}^{2}-2\left(1+\theta \right) N_0+\theta \right] f^2}{\left(1+fP_0 \right) ^3}$, $b_7 = \frac{\left[ N_0^3-\left(1+\theta \right) N_0^2+\theta N_0 \right] f^3}{\left(1+fP_0 \right) ^4}$.

From the characteristic polynomial (2.2), we obtain $f\left(-1 \right) = \frac{h^2}{\epsilon}\left[ \frac{m\left(n-1 \right) \left(n-2 \right)}{fn} \right] +\frac{h}{\epsilon}\left[ \frac{4m\left(1+\theta -2m \right)}{n} \right] +4$.

Since step size $h > 0$, the bifurcation parameter is chosen as

where parameter $m$ satisfies $\frac{1+\theta}{2} < m < 1$.

Consider parameter $h$ with a small perturbation $\delta$, i.e., $h = h^*+\delta$, $\left| \delta \right|\ll 1$, and the system (3.3) becomes

The characteristic polynomial of (3.4) is given by

The transversal condition at $\left(N_0, P_0 \right)$ is

If $\frac{dg(\lambda)}{d\delta}\mid_{\lambda = -1, \delta = 0}^{}\ne0$, then Flip bifurcation will occur at $E_4$.

3.2.   The direction of Flip bifurcation at $E_4$

To facilitate discussion, define $A = \left({\begin{array}{*{20}{c}} 1+\frac{h^*}{\epsilon}\left[ \frac{2m\left(1+\theta -2m \right)}{n} \right] & \, \, \frac{\, \, h^*}{\epsilon}\left[ \frac{-2m\left(n-1 \right)}{n} \right]\\ \frac{h^*\left(n-2 \right)}{2f} & \, \, \, \, 1\\ \end{array}} \right)$.

If the eigenvalue of $A$ goes for $\lambda = -1$, the corresponding eigenvector is given as:

If the eigenvalue of $A$ goes for $\lambda = \lambda _2$, the corresponding eigenvector is given as:

Then, we have the invertible matrix

Using translation $\left(\!\!\begin{array}{c} x_n\\ y_n\\ \end{array} \!\!\right) = T^{-1}\left(\begin{array}{c} \overline{N_n}\\ \overline{P_n}\\ \end{array} \right)$, system (3.4) turns into

where

Using translation $\left(\!\! \begin{array}{c} \overline{N_{n+1}}\\ \overline{P_{n+1}}\\ \end{array} \!\!\right) = T\left(\!\!\begin{array}{c} x_{n+1}\\ y_{n+1}\\ \end{array}\!\! \right)$, system (3.5) becomes

where

$k_{11} = k_{12} = \frac{h^*}{\epsilon}\left[ \frac{-2m\left(n-1 \right)}{n} \right]$, $k_{21} = -2-\frac{h^*}{\epsilon}\left[ \frac{2m\left(1+\theta -2m \right)}{n} \right]$, $k_{22} = \lambda _2-1-\frac{h^*}{\epsilon}\left[ \frac{2m\left(1+\theta -2m \right)}{n} \right]$

Next, by using the center manifold theorem and normal form theories, the direction of Flip bifurcation at $E_4$ is given.

where the coefficients of $\alpha _1$ and $\alpha _2$ are derived from (3.6).

Theorem 3.1. If $\alpha _1\ne 0$, $\alpha _2\ne 0$, then the system undergoes Flip bifurcation at the immobile point $\left(N_0, P_0 \right)$, and if $\alpha _2 > 0\left(<0 \right)$, then the two-cycle point is stable (unstable).

For sufficiently small neighborhoods of the parameter $\delta = 0$, there exists a central manifold at $\left(0, 0 \right)$:

Substituting (3.7) into (3.6), the solution is given as

Restricting the system of equations on $W^c\left(0, 0 \right)$, the results are as follows.

where $l_1 = e_{11} = b_{11}k_{11}^2+b_{12}k_{11}k_{21}+b_{13}k_{21}^2$, $l_2 = d_{11} = a_{11}k_{11}+a_{12}k_{21}$, $l_3 = d_{12}m_1+f_{11}+e_{12}m_2$, $l_4 = d_{12}m_2$, $l_5 = e_{12}m_1+e_{14}$.

According to the normal form theories related to bifurcation analysis, we require the following quantity at $\left(x, y, \delta \right) = \left(0, 0, 0 \right)$.

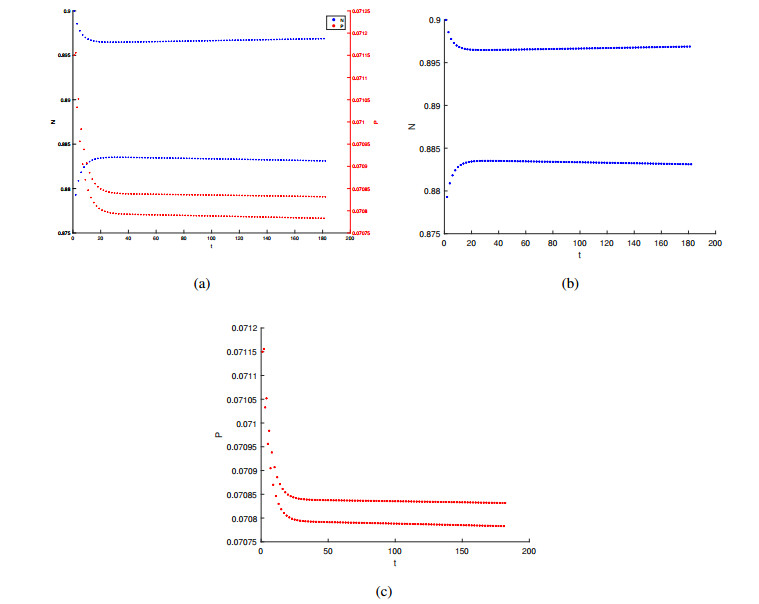
For numerical simulations, we choose the following parameters to prove our theoretical discussion. The unique positive equilibrium point $\left(N_0, P_0 \right) \approx \left(0.89, 0.0708765 \right)$ of the model can be obtained by giving the parameters $h = 0.1$, $e = 0.023933614$, $\theta = 0.2$, $f = 1$, $m = 0.89$. By choosing the initial value of $\left(0.9, 0.07115 \right)$, the result can be obtained by numerical simulation as Figure 1.

It is obvious from the diagrams that variables $N$ and $P$ appear as two-point solutions with a period for a given parameter condition and gradually stabilize near the equilibrium point, which verifies Flip bifurcation occurs at this point.

4.   Hopf bifurcation at $E_4$

In this section, we still choose $h$ as the bifurcation parameter to discuss Hopf bifurcation around its positive equilibrium $\left(N_0, P_0 \right)$. The necessary conditions for Hopf bifurcation to occur is given by the following curve:

where $E = \frac{h}{\epsilon}\left(\frac{m\left(1+\theta -2m \right)}{1+\sqrt{1+4f\left(1-m \right) \left(m-\theta \right)}} \right) +2$.

4.1.   Existence condition of Hopf bifurcation at $E_4$

For emergence of Hopf bifurcation around positive equilibrium $\left(N_0, P_0 \right)$, two roots of the characteristic polynomial (2.2) must be complex conjugate with unit modulus. Therefore, it is easy to obtain the bifurcation parameter $h_1^* = \frac{\left(2m-\theta -1 \right) \left(1+\sqrt{1+4f\left(1-m \right) \left(m-\theta \right)} \right)}{2\left(1-m \right) \left(m-\theta \right) \sqrt{1+4f\left(1-m \right) \left(m-\theta \right)}} > 0$, $i.e.$, $0 < m < \theta$ or $\frac{1+\theta}{2} < m < 1$.

We still consider parameter $h$ with a small perturbation $\delta$, and then characteristic equation (2.2) can be rewritten as:

where

The roots of the characteristic equation of $J\!\mid_{\left(N_0, P_0 \right)}^{}$ are

Also,

where $\frac{d\left| \lambda _{1, 2} \right|}{d\delta}\mid_{\delta = 0}^{} > 0$ if and only if $\frac{\left(1+\theta -2m \right) \left(m-2 \right)}{\epsilon n} > 0$.

If $p\left(0 \right) \ne 0, 1$, we have $-\frac{4f\left(2m-1-\theta \right) ^2}{\epsilon n\left(n-1 \right) \left(n-2 \right)}\ne 2, 3$, which means $\lambda _{1, 2}^n\ne 1\, \ n = 1, 2, 3, 4$.

The transversal condition at $\left(N_0, P_0 \right)$ is given by

If $\frac{1+\theta}{2} < m < 1$, we have $\frac{d\left| \lambda _1 \right|^2}{d\delta}\mid_{\delta = 0}^{} > 0$. Then, Hopf bifurcation will occur at $\left(N_0, P_0 \right)$.

4.2.   The direction of Hopf bifurcation at $E_4$

Now, let

The invertible matrix $T$ is given by

Using the following translation

Then, the Eq (3.4) transforms to

where

Next, by using the center manifold theorem and normal form theories, the direction of Hopf bifurcation at $E_4$ is given. According to the normal form theories related to bifurcation analysis, we require the following quantity at $\left(x, y, \delta \right) = \left(0, 0, 0 \right)$.

where

Theorem 4.1. If the above conditions hold, and $L\ne 0$, the Hopf bifurcation occurs at the point $\left(N_0, P_0 \right)$. When $\delta > 0$, if $L < 0$, then it attracts at that point; when $\delta < 0$, if $L > 0$, then it repels at that point.

To verify whether the condition is correct, we select the following parameters for numerical simulations and obtain the following conclusions. By selecting the first set of parameters $h\approx 0.062163$, $e = 1$, $\theta = 0.1$, $f = 1$, $m = 0.554$, the unique positive equilibrium point $\left(N_0, P_0 \right) \approx \left(0.554, 0.004932 \right)$ of the model can be obtained. By choosing the initial value $K_1 = \left(0.5, 0.005 \right)$, the following results can be obtained by numerical simulation.

Figure 2 reflects that variable $N$ gradually tends to oscillate steadily at the equilibrium point $N = 0.554$ with the increase of the number of iterations $n$, while variable $P$ also gradually oscillates steadily with the increase of the number of iterations $N$, but the equilibrium point is attracted to $P\approx 0.157$.

By choosing the second set of parameters $h\approx 1.120901$, $e = 1$, $\theta = 0.61$, $f = 1$, $m = 0.823$ the only internal equilibrium point $\left(N_0, P_0 \right) \approx \left(0.823, 0.020442 \right)$ of the model can be obtained. Choosing the initial value $K_2 = \left(0.8, 0.02 \right)$, the following results can be obtained by numerical simulation.

Figure 3 shows that as the number of iterations $n$ increases, eventually, the variable $P$ will also be attracted to stabilize at $P\approx 0.035$.

5.   Chaos analysis

In this section, chaotic cases at bifurcating points are analyzed using numerical simulations. We give maximum Lyapunov exponents and phase diagrams for different perturbation parameters to prove our results. The chaos theory analysis of Flip bifurcation and Hopf bifurcation is given as follows.

Definition 5.1. ^[27] The formula for the maximum Lyapunov index is given by

Theorem 5.1. ^[27] If $\lambda < 0$, the neighboring points eventually come together and merge into a single point, which corresponds to stable immobile points and periodic motion. If $\lambda > 0$, the neighboring points eventually separate, which corresponds to local instability of the orbit generating chaotic situations.

In the following, we choose two different equilibria to consider the Flip bifurcation with chaotic cases. Initially, we select the parameters $h = 0.95$, $e\approx 0.1841359$, $\theta = 0.5$, $f = 1$, $m = 0.961$, and obviously the model comes to

where the internal equilibrium point is $\left(N_1, P_1 \right) \approx \left(0.961, 0.01807 \right)$.

After selecting the perturbation $\delta \in \left(0, 0.2 \right)$ and analyzing the trend of $N$ with $\delta$ by numerical simulation, we obtain the chaotic bifurcating cases (see Figure 4).

Next, choosing the parameters $h = 0.95$, $e\approx 0.184136$, $\theta = 0.5$, $f = 1$, $m = 0.9601$, we obtain the model

Obviously, the internal equilibrium point $\left(N_2, P_2 \right) \approx \left(0.9601, 0.0180734 \right)$. We still choose the perturbation $\delta \in \left(0, 0.2 \right)$ to analyze the trend of $N$ with $\delta$. The chaotic bifurcating case is obtained (see Figure 5). By calculating the bifurcating diagrams and the maximum Lyapunov exponent for two bifurcating points with small differences, it can be shown that the small change of the initial value near the equilibrium point has a great influence on the stability of the initial state. Although they are different perturbed bifurcating cases, the two cases tend to go the same during the process of $\delta$ gradually increasing.

In the following, we choose two different equilibria to consider Hopf bifurcation with chaotic cases. By picking the first set of parameters $h\approx 0.062163$, $e = 1$, $\theta = 0.1$, $f = 1$, $m = 0.554$, the unique internal equilibrium point $\left(N_3, P_3 \right) \approx \left(0.554, 0.004932 \right)$ of the model can be obtained.

After choosing perturbation $\delta \in \left(0, 0.5 \right)$, we obtain phase diagrams (see Figure 6).

The analysis mentioned above shows that with the perturbation $\delta$ increasing, the asymptotic stability of variable $N$ gradually becomes weaker, and the range of periodic solutions gradually becomes larger, but the convergence speed comes faster increases (see Figure 6).

By choosing the second set of parameters $h\approx 1.120901$, $e = 1$, $\theta = 0.61$, $f = 1$, $m = 0.823$, we can obtain the unique internal equilibrium point $\left(N_4, P_4 \right) \approx \left(0.823, 0.020442 \right)$ of the model.

After choosing perturbation $\delta \in \left(-1, 1 \right)$, we obtain phase diagrams (see Figure 7).

6.   Conclusions

Our work deals with the study of local dynamical properties of a predator-prey model with discrete time (1.2), Flip bifurcation and Hopf bifurcation associated with the periodic solution, as well as their chaotic cases. We prove that the system (1.2) has four unique equilibria. In addition, their stability and instability conditions are given, which mark the final equilibrium state of both groups as fear, climate and other factors change. We focus on the unique positive equilibrium point $E_4 = \left(m, \frac{-1+\sqrt{1+4f\left(1-m \right) \left(m-\theta \right)}}{2f} \right)$, with stability condition:

Significantly, after analyzing the formation conditions of Flip bifurcation and Hopf bifurcation at $(N_0, P_0)$, we give their chaotic scenarios from both theoretical and numerical simulations. Moreover, it is found that Flip bifurcation is more prone to chaos scenarios, and Hopf bifurcation is closely related to periodic solutions.

Biologically, the occurrence of Flip bifurcation implies the number of predators and prey will alternate around a value instead of converging to a fixed value, eventually. The corresponding chaotic scenario suggests that small perturbations in the variable parameters will eventually have a significant impact on the population, ultimately leading to chaos. The appearance of Hopf bifurcation points indicates that the equilibrium point of the system loses its attraction and eventually produces a closed orbit, which implies the existence of periodic oscillations of predators and prey. Therefore, we can precisely change the biological density of predators and prey to achieve the desired goal by regulating the number of bifurcation parameters $h$, for the fact that the chaotic scenario does not exist. All the conclusions illustrate the effect of fear on populations. Finally, the accuracy of the theory is demonstrated using the maximum Lyapunov exponent and phase diagrams.

In future work, the model can be investigated using different discrete methods. In addition, to obtain specific biological properties, new bifurcation parameters can be selected for the study to obtain the desired conclusions.

Conflict of interest

The authors declare that they have no competing interests.