Newly defined fuzzy Misbalance Prodeg Index with application in multi-criteria decision-making

1.   Introduction

The nonsingular $H$-matrix and its subclass play an important role in a lot of fields of science such as computational mathematics, mathematical physics, and control theory, see ^[1,2,3,4]. Meanwhile, the infinity norm bounds of the inverse for nonsingular $H$-matrices can be used in convergence analysis of matrix splitting and matrix multi-splitting iterative methods for solving large sparse systems of linear equations ^[5], as well as bounding errors of linear complementarity problems ^[6,7]. In recent years, many scholars have developed a deep research interest in the infinity norm of the inverse for special nonsingular $H$-matrices, such as $GSDD_{1}$ matrices ^[8], $CKV$-type matrices ^[9], $S$-$SDDS$ matrices ^[10], $S$-Nekrasov matrices ^[11], $S$-$SDD$ matrices ^[12], and so on, which depends only on the entries of the matrix.

In this paper, we prove that $M$ is a nonsingular $H$-matrix by constructing a scaling matrix $D$ for $SDD_1^{+}$ matrices such that $MD$ is a strictly diagonally dominant matrix. The use of the scaling matrix is important for some applications, for example, the infinity norm bound of the inverse ^[13], eigenvalue localization ^[3], and error bounds of the linear complementarity problem ^[14]. We consider the infinity norm bound of the inverse for the $SDD_1^{+}$ matrix by multiplying the scaling matrix, then we use the result to discuss the error bounds of the linear complementarity problem.

For a positive integer $n\geq 2$, let $N$ denote the set $\{1, 2, \ldots, n\}$ and $C^{n \times n}(R^{n \times n})$ denote the set of all complex (real) matrices. Successively, we review some special subclasses of nonsingular $H$-matrices and related lemmas.

Definition 1. ^[5] A matrix $M = (m_{ij})\in C ^{n\times n}$ is called a strictly diagonally dominant ($SDD$) matrix if

where ${r_i}\left(M \right) = \sum\limits_{j = 1, j \ne i}^n {\left| {{m_{ij}}} \right|}$.

Various generalizations of $SDD$ matrices have been introduced and studied in the literatures, see ^{[7,15,16,17,18]}.

Definition 2. ^[8] A matrix $M = (m_{ij})\in C^{n\times n}$ is called a generalized $SDD_1$ ($GSDD_1$) matrix if

where $N_1 = \left\{ i\in N|0 < |m_{ii}|\leq {r_i}\left(M \right)\right\}$, $N_2 = \left\{ i\in N||m_{ii}| > {r_i}\left(M \right)\right\}$, ${p_{i}^{N_2}}\left(M \right) = \sum\limits_{j \in N_2\backslash \left\{i\right\}}|m_{ij}|\frac{{r_j}\left(M \right)}{|m_{jj}|}$, ${p_{i}^{N_1}}\left(M \right) = \sum\limits_{j \in N_1\backslash \left\{i\right\}}|m_{ij}|, i\in N.$

Definition 3. ^[9] A matrix $M = (m_{ij}) \in {C^{n \times n}}$, with $n\geqslant2$, is called a $CKV$-type matrix if for all $i \in N$ the set $S_{i}^{\star}\left(M\right)$ is not empty, where

with $\sum(i) = \{S \subsetneq N: i \in S\}$ and $r_{i}^{S}\left(M \right) : = \sum\limits_{j \in S\backslash \left\{ i \right\}} {\left| {{m_{ij}}} \right|}.$

Lemma 1. ^[8] Let $M = (m_{ij})\in C^{n\times n}$ be a $GSDD_1$ matrix. Then

where

and

Lemma 2. ^[8] Suppose that $M = (m_{ij})\in R^{n\times n}$ is a $GSDD_1$ matrix with positive diagonal entries, and $D = diag(d_i)$ with $d_i\in[0, 1]$. Then

where $\phi_i, \; \psi_i, and \; \varepsilon$ are shown in (1.4)–(1.6), respectively.

Definition 4. ^[19] Matrix $M = (m_{ij})\in C^{n\times n}$ is called an $SDD_1$ matrix if

where

The rest of this paper is organized as follows: In Section 2, we propose a new subclass of nonsingular $H$-matrices referred to $SDD_1^{+}$ matrices, discuss some of the properties of it, and consider the relationships among subclasses of nonsingular $H$-matrices by numerical examples, including $SDD_1$ matrices, $GSDD_1$ matrices, and $CKV$-type matrices. At the same time, a scaling matrix $D$ is constructed to verify that the matrix $M$ is a nonsingular $H$-matrix. In Section 3, two methods are utilized to derive two different upper bounds of infinity norm for the inverse of the matrix (one with parameter and one without parameter), and numerical examples are used to show the validity of the results. In Section 4, two error bounds of the linear complementarity problems for $SDD_1^{+}$ matrices are given by using the scaling matrix $D$, and numerical examples are used to illustrate the effectiveness of the obtained results. Finally, a summary of the paper is given in Section. 5.

2.   $SDD_1^{+}$ matrices and scaling matrices

For the sake of the following description, some symbols are first explained:

By the definitions of $N_{1}^{(1)}$ and $N_{2}^{(1)}$, for $N_1 = N_{1}^{(1)}\cup N_{2}^{(1)}$, ${r_i}^{\rm{'}}\left(M \right)$ in Definition 4 can be rewritten as

According to (2.4), it is easy to get the following equivalent form for $SDD_1$ matrices.

A matrix $M$ is called an $SDD_1$ matrix, if

By scaling conditions (2.5), we introduce a new class of matrices. As we will see, these matrices belong to a new subclass of nonsingular $H$-matrices.

Definition 5. A matrix $M = (m_{ij})\in C^{n\times n}$ is called an $SDD_1^{+}$ matrix if

where $N_1, N_2, \; N_1^{(1)}, \; N_2^{(1)}, and \; {r_i}^{\rm{'}}(M)$ are defined by (2.1)–(2.3), respectively.

Proposition 1. If $M = (m_{ij})\in C^{n\times n}$ is an $SDD_1^{+}$ matrix and $N_{1}^{(1)}\neq \emptyset$, then $\sum\limits_{j \in N_2^{(1)} }\left|m_{i j}\right|+\sum\limits_{j \in N_2}\left|m_{i j}\right|\neq 0$ for $i\in N_{1}^{(1)}$.

Proof. Assume that there exists $i\in N_{1}^{(1)}$ such that $\sum\limits_{j \in N_2^{(1)} }\left|m_{i j}\right|+\sum\limits_{j \in N_2}\left|m_{i j}\right| = 0$. We find that

which contradicts $i\in N_{1}^{(1)}$. The proof is completed. □

Proposition 2. If $M = (m_{ij})\in C^{n\times n}$ is an $SDD_1^{+}$ matrix with $N_2^{(1)} = \emptyset$, then $M$ is also an $SDD_1$ matrix.

Proof. From Definition 5, we have

Because of $N_1 = N_1^{(1)}$, it holds that

The proof is completed. □

Example 1. Consider the following matrix:

In fact, $N_1 = \left\{1, 2\right\}$ and $N_2 = \left\{3, 4\right\}$. Through calculations, we obtain that

Because of $|m_{11}| = 8 < 8.1333 = {r_1}^{\rm{'}}\left(M_1\right)$, $M_1$ is not an $SDD_1$ matrix.

Since

then $N_1^{(1)} = \left\{1\right\}$, $N_2^{(1)} = \left\{2\right\}$. As

$M_1$ is an $SDD_1^{+}$ matrix by Definition 5.

Example 2. Consider the following matrix:

In fact, $N_1 = \left\{2\right\}$ and $N_2 = \left\{1, 3\right\}$. By calculations, we get

Because of $|m_{22}| = 7 > 6.5375 = {r_2}^{\rm{'}}\left(M_2\right)$, $M_2$ is an $SDD_1$ matrix.

According to

we know that $N_2^{(1)} = \left\{2\right\}$. In addition,

and $M_2$ is not an $SDD_1^{+}$ matrix.

As shown in Examples 1 and 2 and Proposition 2, it can be seen that $SDD_1^{+}$ matrices and $SDD_1$ matrices have an intersecting relationship:

The following examples will demonstrate the relationships between $SDD_1^{+}$ matrices and other subclasses of nonsingular $H$-matrices.

Example 3. Consider the following matrix:

In fact, $N_1 = \left\{2, 3\right\}$ and $N_2 = \left\{1, 4, 5\right\}$. Through calculations, we get that

and $N_1^{(1)} = \left\{2\right\}$, $N_2^{(1)} = \left\{3\right\}$. Because of

So, $M_3$ is an $SDD_1^{+}$ matrix. However, since $|m_{22}| = 10 < 11.9 = r_{2}^{\rm{'}}\left(M_3\right)$, then $M_3$ is not an $SDD_1$ matrix. And we have

Note that, taking $i = 1, j = 2$, we have that

So, $M_3$ is not a $GSDD_1$ matrix. Moreover, it can be verified that $M_3$ is not a $CKV$-type matrix.

Example 4. Consider the following matrix:

It is easy to check that $M_4$ is a $CKV$-type matrix and a $GSDD_1$ matrix, but not an $SDD_1^{+}$ matrix.

Example 5. Consider the following matrix:

We know that $M_5$ is not only an $SDD_1^{+}$ matrix, but also $CKV$-type matrix and $GSDD_1$ matrix.

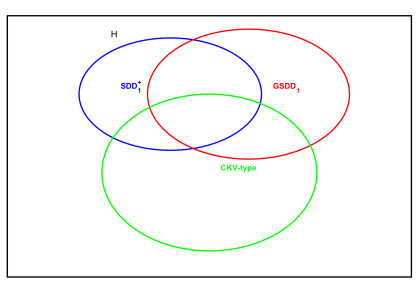
According to Examples 3–5, we find that $SDD_1^{+}$ matrices have intersecting relationships with the $CKV$-type matrices and $GSDD_1$ matrices, as shown in the Figure 1 below. In this paper, we take $N_1\neq\emptyset$ and $r_i(M)\neq 0$, so we will not discuss the relationships among $SDD$ matrices, $SDD_1^{+}$ matrices, and $GSDD_1$ matrices.

Example 6. Consider the tri-diagonal matrix $M\in R^{n\times n}$ arising from the finite difference method for free boundary problems ^[8], where

Take $n = 12000$, $a = 5.5888$, $b = 16.5150$, $c = 10.9311$, and $\alpha = 14.3417$. It is easy to verify that $M_6$ is an $SDD_1^{+}$ matrix, but not an $SDD$ matrix, a $GSDD_1$ matrix, an $SDD_1$ matrix, nor a $CKV$-type matrix.

As is shown in ^[19] and ^[8], $SDD_1$ matrix and $GSDD_1$ matrix are both nonsingular $H$-matrices, and there exists an explicit construction of the diagonal matrix $D$, whose diagonal entries are all positive, such that $MD$ is an $SDD$ matrix. In the following, we construct a positive diagonal matrix $D$ involved with a parameter that scales an $SDD_1^{+}$ matrix to transform it into an $SDD$ matrix.

Theorem 1. Let $M = (m_{ij})\in C^{n\times n}$ be an $SDD_1^{+}$ matrix. Then, there exists a diagonal matrix $D = diag(d_1, d_2, \cdots, d_n)$ with

where

and for all $i \in N_1^{(1)}$, we have

such that $MD$ is an $SDD$ matrix.

Proof. By (2.6), we have

From Proposition 1, for all $i \in N_1^{(1)}$, it is easy to know that

Immediately, there exists a positive number $\varepsilon$ such that

Now, we construct a diagonal matrix $D = diag(d_1, d_2, \cdots, d_n)$ with

where $\varepsilon$ is given by (2.12). It is easy to find that all the elements in the diagonal matrix $D$ are positive. Next, we will prove that $MD$ is strictly diagonally dominant.

Case 1. For each $i\in N_1^{(1)}$, it is not difficult to find that $|\left(MD\right)_{ii}| = |m_{ii}|$. By (2.11) and (2.13), we have

Case 2. For each $i\in N_2^{(1)}$, we obtain

From (2.3), (2.13), and (2.14), we derive that

The first inequality holds because of $|m_{ii}| > r_i^{\prime}(M)$ for any $i\in N_2^{(1)}$, and

Case 3. For each $i\in N_2$, we have

Meanwhile, for each $i\in N_2$, it is easy to get

and

From (2.13), (2.15), and (2.16), it can be deduced that

So, $\left|(M D)_{i i}\right| > r_i(MD)$ for $i\in N$. Thus, $MD$ is an $SDD$ matrix. The proof is completed. □

It is well known that the $H$-matrix $M$ is nonsingular if there exists a diagonal matrix $D$ such that $MD$ is an $SDD$ matrix (see ^[1,19]). Therefore, from Theorem 1, $SDD_1^{+}$ matrices are nonsingular $H$-matrices.

Corollary 1. Let $M = (m_{ij})\in C^{n\times n}$ be an $SDD_1^{+}$ matrix. Then, $M$ is also an $H$-matrix. If, in addition, $M$ has positive diagonal entries, then $det(M) > 0$.

Proof. We see from Theorem 1 that there is a positive diagonal matrix $D$ such that $MD$ is an $SDD$ matrix (cf. (M35) of Theorem 2.3 of Chapter 6 of ^[1]). Thus, $M$ is a nonsingular $H$-matrix. Since the diagonal entries of $M$ and $D$ are positive, $MD$ has positive diagonal entries. From the fact that $MD$ is an $SDD$ matrix, it is well known that $0 < det(MD) = det(M)det(D)$, which means $det(M) > 0$. □

3.   Infinity norm bounds of the inverse of $SDD_1^{+}$ matrices

In this section, we start to consider two infinity norm bounds of the inverse of $SDD_1^{+}$ matrices. Before that, some notations are defined:

Next, let us review an important result proposed by Varah (1975).

Theorem 2. ^[20] If $M = (m_{ij})\in C^{n\times n}$ is an $SDD$ matrix, then

Theorem 2 can be used to bound the infinity norm of the inverse of an $SDD$ matrix. This theorem together with the scaling matrix $D = diag(d_1, d_2, \cdots, d_n)$ allows us to gain the following Theorem 3.

Theorem 3. Let $M = (m_{ij})\in C^{n\times n}$ be an $SDD_1^{+}$ matrix. Then,

where $\varepsilon$, $M_i, \; N_i, \; and\; Z_i$ are defined in (2.8), (2.9), and (3.1)–(3.3), respectively.

Proof. By Theorem 1, there exists a positive diagonal matrix $D$ such that $MD$ is an $SDD$ matrix, where $D$ is defined as (2.13). Hence, we have the following result:

and

where $\varepsilon$ is given by (2.8). Note that $MD$ is an $SDD$ matrix, by Theorem 2, we have

However, there are three scenarios to solve $\left|\left(MD\right)_{i i}\right|-{r_i}\left(MD\right)$. For $i\in N_1^{(1)}$, we get

For $i\in N_2^{(1)}$, we have

For $i\in N_2$, we obtain

Hence, according to (3.6) we have

The proof is completed. □

It is noted that the upper bound in Theorem 3 is related to the interval values of the parameter. Next, another upper bound of $\left\|M^{-1}\right\|_{\infty}$ is given, which depends only on the elements in the matrix.

Theorem 4. Let $M = (m_{ij})\in C^{n\times n}$ be an $SDD_1^{+}$ matrix. Then,

where $F_i(M)$ and $F_i^{\prime}(M)$ are shown in (2.6).

Proof. By the well-known fact (see^[21,22]) that

for some $x = [x_1, x_2, \cdots, x_n]^T$, we have

Assume that there is a unique $k \in N$ such that $\|x\|_{\infty} = 1 = |x_k|$, then

When $k\in N_1^{(1)}$, let $\left|x_j\right| = \frac{r_j^{\prime}(M)}{\left|m_{j j}\right|}$ ($j\in N_2^{(1)}$), and $\left|x_j\right| = \frac{r_j(M)}{\left|m_{j j}\right|}$ ($j \in N_2$). Then we have

Which implies that

For $k\in N_2^{(1)}$, let $\sum\limits_{j \in N_1^{(1)}}\left|m_{k j}\right| = 0$. It follows that

Hence, we obtain that

For $k\in N_2$, we get

and

which implies that

To sum up, we obtain that

The proof is completed. □

Next, some numerical examples are given to illustrate the superiority of our results.

Example 7. Consider the following matrix:

It is easy to verify that $M_7$ is an $SDD_1^{+}$ matrix. However, we know that $M_7$ is not an $SDD$ matrix, a $GSDD_1$ matrix, an $SDD_1$ matrix and a $CKV$-type matrix. By the bound in Theorem 3, we have

When $\varepsilon = 0.1225$, we get

The range of parameter values in Theorem 3 is not empty set, and its optimal solution can be illustrated through examples. In Example 7, the range of values for the error bound and its optimal solution can be seen from Figure 2. The bound for Example 7 is (8.1633,100), and the optimal solution for Example 7 is 8.1633.

However, according to Theorem 4, we obtain

Through this example, it can be found that the bound of Theorem 4 is better than Theorem 3 in some cases.

Example 8. Consider the following matrix:

Here, $a = -2$, $c = 2.99$, $b_1 = 6.3304$, $b_2 = 6.0833$, $b_3 = 5.8412$, $b_4 = 5.6065$, $b_5 = 5.3814$, $b_6 = 5.1684$, $b_7 = 4.9695$, $b_8 = 4.7866$, $b_9 = 4.6217$, and $b_{10} = 4.4763$. It is easy to verify that $M_8$ is an $SDD_1^{+}$ matrix. However, we can get that $M_8$ is not an $SDD$ matrix, a $GSDD_1$ matrix, an $SDD_1$ matrix, and a $CKV$-type matrix. By the bound in Theorem 3, we have

When $\varepsilon = 0.01$, we have

If $\varepsilon = 0.1$, we have

Taking $\varepsilon = 0.11$, then it is easy to calculate

By the bound in Theorem 4, we have

Example 9. Consider the following matrix:

It is easy to verify that the matrix $M_9$ is a $GSDD_1$ matrix and an $SDD_1^{+}$ matrix. When $M_9$ is a $GSDD_1$ matrix, it can be calculated according to Lemma 1 that

According to Figure 3, if we take $\varepsilon = 1.0964$, we can obtain an optimal bound, namely

When $M_9$ is an $SDD_1^{+}$ matrix, it can be calculated according to Theorem 3. We obtain

According to Figure 3, if we take $\varepsilon = 0.1707$, we can obtain an optimal bound, namely

However, according to Theorem 4, we get

Example 10. Consider the following matrix:

It is easy to verify that the matrix ${M}_{10}$ is a $C K V$-type matrix and an $S D D_1^{+}$ matrix. When ${M}_{10}$ is a $CKV$-type matrix, it can be calculated according to Theorem 21 in ^[9]

When ${M}_{10}$ is an $S D D_1^{+}$matrix, take $\varepsilon = 0.0914$ according to Theorem 3. We obtain an optimal bound, namely

When ${M}_{10}$ is an $S D D_1^{+}$matrix, it can be calculated according to Theorem 4. We can obtain

From Examples 9 and 10, it is easy to know that the bound in Theorem 3 and Theorem 4 in our paper is better than available results in some cases.

4.   Error bound of the LCP associated with $SDD_1^{+}$ matrices

The $P$-matrix refers to a matrix in which all principal minors are positive ^[19], and it is widely used in optimization problems in economics, engineering, and other fields. In fact, the linear complementarity problem in the field of optimization has a unique solution if and only if the correlation matrix is a $P$-matrix, so the $P$-matrix has attracted extensive attention, see ^[23,24,25]. As we all know, the linear complementarity problem of matrix $M$, denoted by $LCP(M, q)$, is to find a vector $x\in R^{n}$ such that

or to prove that no such vector $x$ exists, where $M\in R^{n\times n}$ and $q\in R^{n}$. One of the essential problems in $LCP(M, q)$ is to estimate

where $D = diag(d_{i})$, $d = (d_{1}, d_{2}, \cdots, d_{n})$, $0\leq d_{i}\leq 1$, $i = 1, 2, \cdots, n$. It is well known that when $M$ is a $P$-matrix, there is a unique solution to linear complementarity problems.

In ^[2], Chen et al. gave the following error bound for $LCP(M, q)$,

where $x^{*}$ is the solution of $LCP(M, q)$, $r(x) = \min\{x, Mx+q\}$, and the min operator $r(x)$ denotes the componentwise minimum of two vectors. However, for P-matrices that do not have a specific structure and have a large order, it is very difficult to calculate the error bound of $\max\limits_{d\in [0, 1]^{n}} \| (I-D+DM)^{-1}\|_{\infty}$. Nevertheless, the above problem is greatly alleviated when the proposed matrix has a specific structure ^{[7,16,26,27,28]}.

It is well known that a nonsingular $H$-matrix with positive diagonal entries is a $P$-matrix. In ^[29], when the matrix $M$ is a nonsingular $H$-matrix with positive diagonal entries, and there is a diagonal matrix $D$ so that $MD$ is an $SDD$ matrix, the authors propose a method to solve the error bounds of the linear complementarity problem of the matrix $M$. Now let us review it together.

Theorem 5. ^[29] Assume that $M = (m_{ij})\in R^{n\times n}$ is an $H$-matrix with positive diagonal entries. Let $D = diag(d_i)$, $d_i > 0$, for all $i \in N = \left\{1, \ldots, n\right\}$, be a diagonal matrix such that $MD$ is strictly diagonally dominant by rows. For any $i \in N = \left\{1, \ldots, n\right\}$, let $\beta_i : = m_{ii}d_i-\sum\limits_{j\neq i}|m_{ij}|d_j$. Then,

Next, the error bound of the linear complementarity problem of $SDD_1^{+}$ matrices is given by using the positive diagonal matrix $D$ in Theorem 1.

Theorem 6. Suppose that $M = (m_{ij})\in R^{n\times n}\; (n\geq 2)$ is an $SDD_1^{+}$ matrix with positive diagonal entries, and for any $i\in N_{1}^{(1)}$, $\sum\limits_{j \in N_2^{(1)} }\left|m_{i j}\right|+\sum\limits_{j \in N_2}\left|m_{i j}\right|\neq 0$. Then,

where $\varepsilon$, $M_i, \; N_i, \; and\; Z_i$ are defined in (2.8), (2.9), and (3.1)–(3.3), respectively.

Proof. Since $M$ is an $SDD_1^{+}$ matrix with positive diagonal elements, the existence of a positive diagonal matrix $D$ such that $MD$ is a strictly diagonal dominance matrix can be seen. For $i\in N$, we can get

By Theorem 5, for $i\in N_1^{(1)}$, we get

For $i\in N_2^{(1)}$, we have

For $i\in N_2$, we have

To sum up, it can be seen that

According to Theorems 1 and 5, it can be obtained that

The proof is completed. □

It is noted that the error bound of Theorem 6 is related to the interval of the parameter $\varepsilon$.

Lemma 3. ^[16] Letting $\gamma > 0$ and $\eta > 0$, for any $x\in[0, 1]$,

Theorem 7. Let $M = ({{m_{ij}}}) \in {R^{n \times n}}$ be an $SDD_{1}^+$ matrix. Then, $\overline {M} = (\overline {m}_{ij}) = I - D + DM$ is also an $SDD_{1}^+$ matrix, where $D = diag\left({{d_i}} \right)$ with $0 \le {d_i} \le 1$, $\forall i\in N$.

Proof. Since $\overline {M} = I-D+DM = (\overline {m}_{ij})$, then

By Lemma 3, for any $i\in N_1^{(1)}$, we have

In addition, $d_i F_i(M) < 1-d_i+d_i\left|m_{i i}\right| = \left|\overline{m}_{i i}\right|$, that is, for each $i \in N_1^{(1)}(\overline{M}) \subseteq N_1^{(1)}(M), \left|\overline{m}_{i i}\right| > F_i(\overline{M})$.

For any $i \in N_2^{(1)}$, we have

So, $d_i F_i^{\prime}(M) < 1-d_i+d_i\left|m_{i i}\right| = \left|\overline{m}_{i i}\right|$, that is, for each $i \in N_2^{(1)}(\overline{M}) \subseteq N_2^{(1)}(M), \left|\overline{m}_{i i}\right| > F_i^{\prime}(\overline{M})$. Therefore, $\overline{M} = \left(\overline{m}_{i j}\right) = I-D+D M$ is an $SDD_{1}^+$ matrix. □

Next, another upper bound about $\max\limits _{d \in[0, 1]^n}\left\|(I-D+D M)^{-1}\right\|_{\infty}$ is given, which depends on the result in Theorem 4.

Theorem 8. Assume that $M = (m_{ij})\in R^{n\times n}\; (n\geq 2)$ is an $SDD_1^{+}$ matrix with positive diagonal entries, and ${\overline M} = I-D+DM$, $D = diag\left({{d_i}} \right)$ with $0 \le {d_i} \le 1$. Then,

where $N_2, \; N_1^{(1)}, \; N_2^{(1)}, \; F_i({M}), \; and\; F_i^{\prime}(M)$ are given by (2.1), (2.2), and (2.6), respectively.

Proof. Because $M$ is an $SDD_1^{+}$ matrix, according to Theorem 7, ${\overline M} = I-D+DM$ is also an $SDD_1^{+}$ matrix, where

By (3.7), we can obtain that

According to Theorem 7, for $i \in N_1^{(1)}$, let

we have

For $i \in N_2^{(1)}$, we get

For $i \in N_2$, we can obtain that

To sum up, it holds that

The proof is completed. □

The following examples show that the bound (4.6) in Theorem 8 is better than the bound (4.4) in some conditions.

Example 11. Let us consider the matrix in Example 6. According to Theorem 6, by calculation, we obtain

Taking $\varepsilon = 0.01$, then

In addition, from Theorem 8, we get

Example 12. Let us consider the matrix in Example 9. Since $M_9$ is a $GSDD_1$ matrix, then, by Lemma 2, we get

From Figure 4, when $\varepsilon = 1.0964$, the optimal bound can be obtained as follows:

Moreover, $M_9$ is an $SDD_1^{+}$ matrix, and by Theorem 6, we get

From Figure 4, when $\varepsilon = 0.1794$, the optimal bound can be obtained as follows:

However, according to Theorem 8, we obtain that

Example 13. Consider the following matrix:

Obviously, ${B}^{+} = {M}_{11}$ and ${C} = 0$. By calculations, we know that the matrix ${B}^{+}$ is a ${CKV}$-type matrix with positive diagonal entries, and thus ${M}_{11}$ is a $CKV$-type $B$-matrix. It is easy to verify that the matrix ${M}_{11}$ is an $S D D_1^{+}$ matrix. By bound (4.4) in Theorem 6, we get

By the bound (4.6) in Theorem 8, we get

while by Theorem 3.1 in ^[18], it holds that

From Examples 12 and 13, it is obvious to know that the bounds in Theorems 6 and 8 in our paper is better than available results in some cases.

5.   Conclusions

In this paper, a new subclass of nonsingular $H$-matrices, $SDD_1^{+}$ matrices, have been introduced. Some properties of $SDD_1^{+}$ matrices are discussed, and the relationships among $SDD_1^{+}$ matrices and $SDD_1$ matrices, $GSDD_1$ matrices, and $CKV$-type matrices are analyzed through numerical examples. A scaling matrix $D$ is used to transform the matrix $M$ into a strictly diagonal dominant matrix, which proves the non-singularity of $SDD_1^{+}$ matrices. Two upper bounds of the infinity norm of the inverse matrix are deduced by two methods. On this basis, two error bounds of the linear complementarity problem are given. Numerical examples show the validity of the obtained results.

Author contributions

Lanlan Liu: Conceptualization, Methodology, Supervision, Validation, Writing-review; Yuxue Zhu: Investigation, Writing-original draft, Conceptualization, Writing-review and editing; Feng Wang: Formal analysis, Validation, Conceptualization, Writing-review; Yuanjie Geng: Conceptualization, Validation, Editing, Visualization. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This research is supported by Guizhou Minzu University Science and Technology Projects (GZMUZK[2023]YB10), the Natural Science Research Project of Department of Education of Guizhou Province (QJJ2022015), the Talent Growth Project of Education Department of Guizhou Province (2018143), and the Research Foundation of Guizhou Minzu University (2019YB08).

Conflict of interest

The authors declare no conflicts of interest.