The asymptotic spreading speeds of COVID-19 with the effect of delay and quarantine

1.   Introduction

A severe acute respiratory syndrome coronavirus 2 (SARS-COV-2) spread in Wuhan, China, in December 2019. The novel coronavirus disease has been called COVID-19 by the World Health Organization (WHO) [5]. As of Jan 29, 2020, there were 5993 confirmed cases in China and 132 reported deaths [44]. The numbers increased rapidly to over 77,500 confirmed cases and 2600 deaths as of Feb 24, 2020 [30]. The National Health Commission of China and the Health Commission of local governments report daily the number of new disease cases and their locations. Here, we care about the data reported by these Commissions and by Feng et al. [19] from Jan 17, 2020 to Mar 20, 2020. The results [19, Figure 1] show that the disease outbreak began in Wuhan, and no cases were reported in any other region of the country until Jan 17, 2020. The government of China imposed a lockdown on Wuhan on Jan 23 [19]. The number of cases peaked on February 7 according to [19], and on February 10 according to [14]. The COVID-19 virus was able to spread to other cities despite the government's efforts to control the disease. By the end of February 2020, the number of new cases reported was gradually slowing down [19]. This indicates that the COVID-19 virus was under control within two months [19, Figure 1].

The value of the basic reproduction number is significant in pathology. The basic reproduction number is the average number of people catching a disease from one infectious person [13]. At the early stages of the epidemic in China, the basic reproduction number has been reported between 2 to 3.58 [20,22,24,27,28,30,31,32,42,44,46]. Other authors estimated the mean value of the basic reproduction number to be from 4.8 to 7.08 [5, Figure 1].

Governments have adopted extreme measures, such as social distancing, quarantine, and travel restrictions to minimize the spread of the virus. About a week after applying some of these measures, the basic reproduction number dropped to 1.05 [27]. According to [23], quarantine is the most effective way to contain the disease.

Because of the direct impact of COVID-19 on global health, many mathematical models and studies have been published, see [5,6,12,14,18,19,21,23,24,27,29,36,41,43,44,47]. The current COVID-19 mathematical models are mostly a system of ordinary differential equations [5,6,12,18,21,24,27,29,44]. For mathematical models that consider quarantine and isolation measures, we refer to [14,23,34]. [11] developed a SEIR model to describe the interactions between passengers and crews on a ship and the influence of quarantine to slow the spread of the disease. [14] introduced a model for COVID-19 to investigate the power of isolation and quarantine further. The mathematical model in [47] assumes that individuals are quarantined during the infected or infectious stage. In contrast, the mathematical models in [10,26,35] suggest a possible quarantine for susceptible, infected, and infectious individuals.

Due to the incubation period of COVID-19, infected individuals are subject to some time delay before being transferred to the infectious state. The model we study in this paper describes the infected individuals in the latent period, which makes it more appropriate to investigate the spatial dynamics of COVID-19. Recently, modeling the infection age is more common, and this leads to more complicated mathematical models, see [36,39]. The incubation period ranges from 1 to 14 days [13]. The mean incubation period is three days in [30], from 5 to 6.4 in [42,45]. The mean length of infectious periods is five days in [30] and 1.61 days in [31]. The latent and incubation periods are assumed to be exact [44].

Hence, we propose a model with a time delay due to the incubation period to understand the dynamics of COVID-19 better. Also, we study the influence of quarantine and the values of the parameters on the spatial spreading speeds of COVID-19 in China. This can be done by applying the concept of asymptotic speeds of the spread of an epidemic discussed by Diekmann [15,16,17] and Thieme [37,38], generalized by Thieme and Zhao [40], and applied recently by Alanazi, Jackiewicz, and Thieme [2,4].

According to Diekmann [16,17] and Thieme [37,38], an epidemic can be described by

if there is no increase in the susceptible individuals by birth, immigration, or recovery. In this equation, $u$ is the cumulative rate of infected individuals meeting the susceptible, which describes the development of the population. The initial conditions are collected and listed in $u_0.$ The nonlinear term $G$ contains integral kernels that measure the contribution of infected individuals to the cumulative rate $u.$ Aronson and Weinberger [8,9] and Aronson [7] show that $c^*$ is called the asymptotic speed if the solution $u$ converges to zero uniformly when $|x| \geq ct$ for $c > c^*,$ whereas it is bounded away from zero uniformly when $|x| \leq ct$ for $c < c^*$ after a sufficiently long time $t.$ For more on this, we refer to the work by Ruan [33].

The paper is organized as follows. In Section 2, we consider a mathematical model with quarantine and a generally distributed length of the incubation stage. In Section 3, we reduce the model to a single integral equation where the theory of asymptotic speeds of spread can apply. The definition of the spreading speeds and the basic reproduction number are also introduced in Section 3. Numerical examples are given in Section 4 to confirm some of the analytic findings. The theoretical and numerical results are discussed in Section 5.

2.   COVID-19 model with delay and quarantine

The model assumes the infected individuals of COVID-19 are not infectious during the incubation stage, see [20,44]. Also, quarantining all of the infectious population is not possible. Therefore, we assume that part of the infectious population is non-quarantined.

Let the density of susceptible individuals be denoted by $S(x, t)$, the density of infected individuals in the latent period be $I(x, a, t)$ with infection age $a$, and the density of non-quarantined infectious individuals be $Q(x, t)$. Also, let the infected individuals with infection age $a \in[0, \infty)$ leave the latent period with rate $\ell(a).$ Then, the model takes the form

with $x \in {{ \mathbb{R}}}^n$ and $t > 0.$ The initial densities are

$\eta > 0$ is the disease transmission coefficient, and $\ell > 0$ is the per capita transition rate from the latent (infected) stage to the infectious stage. $\ell$ is a continuous function and $\ell$: $[0, \infty) \rightarrow [0, \infty).$ The effectiveness of quarantine is given by $\gamma,$ where $1 > \gamma \geq 0.$ $1/q > 0$ is the mean length of the infectious period. We assume that the initial are nonnegative continuous functions.

We reduce system (2.1) by integrating along the characteristics for the infected individuals $I(x, a, t)$. Let $a = t+r,$ $i_r(x, t) = I(x, t+r, t),$ and $t_r = \max\{0, -r\},$ where $r \in {{ \mathbb{R}}}.$ Then, the model of infected individuals inside the latent period becomes

for $t\geq t_r.$ Solving, we get

Therefore, for $a > t$,

Let $s \rightarrow s-r.$ Then we get

Let $L(r) = \exp\left(-\int_0^r \ell(s) ds \right).$ Then we conclude

For $t > a$,

Also, let $s \rightarrow s-r.$ Then we have

Therefore, from (2.3), we have

and from (2.4) we have

Substituting (2.5) and (2.6) into (2.1) gives the following system with delay and Volterra integral equations

where

$x \in {{ \mathbb{R}}}^n,$ $t > 0,$ and $\hat{L}(a, t) = \frac{L (a)}{L(a-t)}.$ We define $L(a) = \exp\left(-\int_0^a \ell(s) ds \right)$ to be the probability that infected individuals with infection age $a$ are still in the latent period. Therefore, $L$ is a decreasing function, $L: {{ \mathbb{R}}}_+ \rightarrow [0, 1],$ and $L(0) = 1.$

3.   Spreading speeds of COVID-19

Models 2.7 and 2.8 could be reduced to a single integral equation. We begin this section by integrating the differential equations in (2.7). Therefore, we have

where

and

We substitute (2.8) into (3.3) and do a change of variables several times, and we get the following non-linear equation describing the development of the infectious population,

where

Let $\jmath(x, r) = \eta (1-\gamma) \int_0^r e^{-q s} \ell(r-s) L(r-s) S_0(x) ds.$ Then, (3.4) becomes

We assume that the initial number of susceptible is constant, then apply one side Laplace transform,

We do a change of variables, let $r-s \to r,$ and obtain

We know that $- L'(r) = \ell(r) L(r),$ so we have

By the assumptions in Section 2, we have

By [40], we can use the Laplace transform to find equations for the spreading speeds $c^*$ as follows:

Example 3.1. Let $\rho$ be the mean length of the incubation period. If the incubation stage is uniformly distributed,

and then

Therefore,

The basic reproduction number of COVID-19 can be found by replacing $\lambda$ and $c$ in (3.8) with zero, see [38,40]. Therefore, the basic reproduction number of COVID-19 is given by

According to [16,17,38], the spreading speed is defined by

as long as ${{\mathcal R}}_0 > 1,$ and $c^*: = 0$ if ${{\mathcal R}}_0 \le 1$. Therefore, we have the following results.

Theorem 3.2. Assume the initial conditions $I_0$ and $Q_0$ are defined as $I_0(x, a), Q_{0}(x) \leq \varepsilon e^{-\lambda |x|},$ and $\mid x \mid \geq ct.$ Then $\hat{w}(x, t) \to 0$ as $t \to \infty.$

Proof. $\hat{w}(x, t)$ is given in (3.5). Since $\hat{L}(a, t) = \frac{L (a)}{L(a-t)},$ we have

We change the order of integration as follows:

By the assumptions $I_0(x, a), Q_{0}(x) \leq \varepsilon e^{-\lambda |x|}$, we have

Since $\gamma < 1$ and $\mid x \mid \geq ct,$ $\hat{w}(x, t) \to 0$ as $t \to \infty.$ This completes the proof. □

Theorem 3.3. Let $\hat{\rho} > 0$ be the minimum length of the latent period, $L_1$ be a decreasing function such that $L_1: {{ \mathbb{R}}}_+ \rightarrow [0, 1],$ and $L(a)$ be defined as

Then:

(1) $\mathcal{L}(c, \lambda) \leq \frac{S_0 \eta (1-\gamma)}{ q + \lambda c} e^{-\lambda c \hat{\rho}}.$

(2) $\mathcal{L}(c, \lambda) \to \frac{S_0 \eta (1-\gamma)}{ q + \lambda c}$ as $\hat{\rho} \to 0.$

(3) $\mathcal{L}(c, \lambda) \to 0$ as $\hat{\rho} \to \infty,$ which provides $c^* \leq c.$

(4) $\mathcal{L}(c, \lambda) \to {{\mathcal R}}_0$ as $\lambda \to 0.$

Proof. (1) By (3.7),

The integration by parts of $\int_0^\infty - L'(r) e^{-\lambda cr} dr$ gives

From the definition in (3.15), we get

Let $r-\hat{\rho} \to r.$ Then we have

Therefore,

(2) By (3.16), $\mathcal{L}(c, \lambda) \to \frac{S_0 \eta (1-\gamma)}{ q + \lambda c}$ as $\hat{\rho} \to 0.$

(3) By (3.16), $\mathcal{L}(c, \lambda) \to 0$ as $\hat{\rho} \to \infty.$ By definition (3.13), we conclude $c^* \leq c.$

(4) We clearly have $\mathcal{L}(c, \lambda) \to {{\mathcal R}}_0$ as $\lambda \to 0$ from (3.16). □

Theorem 3.4. Let $L(a)$ be defined as in (3.10). Then, $\mathcal{L}(c, \lambda) \to 0$ as $\lambda \to \infty.$ Also, $\mathcal{L}(c, \lambda) \to 0$ as $\rho \to \infty.$

Proof. By (3.11),

This shows $\mathcal{L}(c, \lambda) \to 0$ by either $\lambda \to \infty$ or $\rho \to \infty.$ □

Theorem 3.5. The spreading speed $c^*$ of COVID-19 is an increasing function of $S_0$ and $\eta.$

Proof. The Laplace transform $\mathcal{L}(c, \lambda)$ is an increasing function of $S_0$, $\eta$, and $d$ for all $c, \lambda > 0.$ By [4, Corollary 8.2], the associated spreading speeds are also increasing functions of these parameters. □

Theorem 3.6. The spreading speed $c^*$ of COVID-19 is a decreasing function with the effectiveness of quarantine $\gamma$ and $q.$

Proof. Since the Laplace transform $\mathcal{L}(c, \lambda)$ is a decreasing function with the effectiveness of quarantine $\gamma$ and $q$ for all $c, \lambda > 0,$ the assertion holds by [4, Corollary 8.2]. □

4.   Numerical experiments

4.1.   Numerical approximations of the basic reproduction number ${{\mathcal R}}_0$ of COVID-19

By (3.12), the basic reproduction number of COVID-19 is

Therefore, the disease is going to spread as long as ${{\mathcal R}}_0 > 1.$ With the given values in Table 1, the threshold density of the susceptible at which ${{\mathcal R}}_0 = 1$ is $S_0^T\approx 1.05 [ \rm{people}/ \rm{km}^2]$ for $\gamma = 0.$ The values of ${{\mathcal R}}_0$ at different values of $S_0$ are demonstrated in Table 2.

4.2.   Propagation of COVID-19

Assuming that the infected individuals leave the latent period with fixed rate $\rho$ such that $\ell(a)$ is one for $0 \leq a < \rho$ and zero otherwise. Then, the model takes the form,

where $x \subseteq {{ \mathbb{R}}}$ and $t \in [0, 60 ]$ is measured in days. The initial densities have been selected as follows:

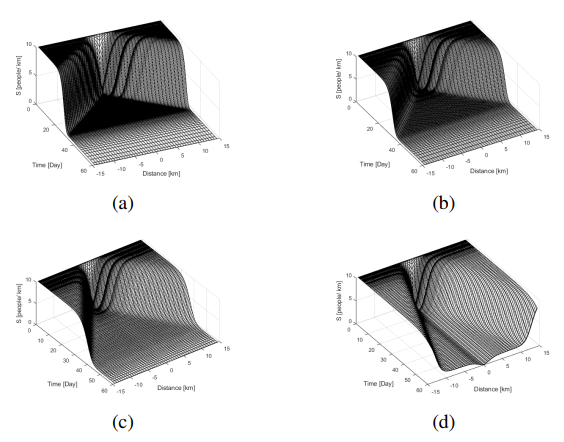
Systems (4.2) and (4.3) are discretized in space. Then, we apply the continuous Runge-Kutta method of the fourth-order and the discrete Runge-Kutta method of the third-order to approximate the solutions in time. This numerical method provides accurate and stable solutions, as discussed in [2,3]. The dynamics of (4.2) and (4.3) are presented in Figures 1–4. The approximated solutions of the density of susceptible $S(x, t)$ are demonstrated in Figure 1, and the approximated solutions of the density of non-quarantined infectious individuals $Q(x, t)$ are shown in Figure 2. The contour plots of $S$ and $Q$ are depicted in Figures 3 and 4. The numerical values of the parameters are chosen from the literature as in Table 1.

5.   Discussion

In this work, we present a mathematical model with time delay and quarantine to study the dynamics of COVID-19. We aim to investigate the influence of the latent period, quarantine, and the values of the parameters on the spatial spreading speeds of COVID-19 in China. We reduce the model to a single equation so that the concept of asymptotic speeds of the spread of an epidemic can be used. In the other part of this work, we provide a numerical simulation to assess our proposed model.

The dynamics of COVID-19 are presented in Figures 1–4. Figure 3 depicts contour plots of the density of susceptible individuals $S(x, t),$ while Figure 4 displays contour plots of the density of non-quarantined infectious individuals $Q(x, t).$ The contour plots in Figures 3 and 4 are essential to predict the spatial spreading speeds of COVID-19. Figure 1 demonstrates the dynamics of the density of susceptible individuals $S(x, t),$ while Figure 2 exhibits the density of non-quarantined infectious individuals $Q(x, t)$ for different scenarios. In the first scenario, we assume that there are no quarantines imposed by the government of China, i.e., $\gamma = 0.$ This choice depicts massive waves in the density of non-quarantined infectious individuals $Q(x, t)$ and huge drops in the density of susceptible individuals $S(x, t).$ Increasing the chance of quarantining infected individuals by $25 \%$ leads to a considerable decrease in the spreading speeds of COVID-19 as in Figures 1(b) and 2(b). Increasing the quarantine rate to $50 \%$ of the infected individuals shows that the first wave of COVID-19 would not hit the boundaries until about 45 days after the pandemic began. The last scenario shows that the disease is under control within two months if we can quarantine $75 \%$ of the infected people. The actual data published by the National Health Commission of China and the Health Commission of local governments during the period from Jan 17, 2020, to Mar 20, 2020, demonstrate that the cumulative number of infected people peaked after twenty days, which is on Feb 7, 2020 [19]. To reduce the spreading speed of the virus, the government of China imposed a lockdown in Wuhan on Jan 23 [19]. The data reported by the National Health Commission of China and the Health Commission of local governments show that the disease of COVID-19 was under control within two months [19, Figure 1]. Therefore, the model demonstrates good qualitative agreement with the actual data published by the National Health Commission of China and the Health Commission of local governments, and is summarized by [19, Figure 1]. This study shall help experts and decision-makers understand the spatial spreading speeds of COVID-19 better and make the necessary efforts to prevent the virus from spreading further.

The numerical results displayed in Table 3–6 are consistent with the analytic results in Theorems 3.5 and 3.6. The spreading speeds of COVID-19 that are given in Tables 3–6 are summarized in Table 7. Tables 3 and 4 indicate that $c^*$ is an increasing function of the initial number of susceptible $S_0$ and the disease transmission coefficient $\eta$ (Theorem 3.5), while Tables 3 and 6 demonstrates that the spreading speeds of COVID-19 is a decreasing function with the effectiveness of quarantine $\gamma$ and with the mean length of the infectious period $1/q$ (Theorem 3.6). Table 5 depicts $c^*$ as a decreasing function with the mean length of the incubation period $\rho.$ Alanazi [1] studied the asymptotic spreading speeds of COVID-19 by assuming that the susceptible, infected, and infectious individuals can diffuse by adding the diffusing coefficients to the model. The results are demonstrated in Table 8 [1, Table 2]. The results demonstrated in Table 8 depict that the diffusion coefficients greatly impact the disease's spreading speed. Overall, the values of the model parameters can highly influence the spreading speeds of COVID-19. Also, Figures 1 and 2 suggest that $S(x, t) \to S_0$ and $Q(x, t) \to 0$ as $\gamma \to 1,$ which clearly show that quarantine measures are constructive and effective in containing the disease.

It is feasible to show that the assumptions of Theorem 2.1 in [40] hold. Therefore, since $\hat{w}(x, t) \to 0$ as $t \to \infty$ (Theorem 3.2), we have $w(x, t) \to 0$ as $t \to \infty$ for $\mid x \mid \geq ct$ and $c > c^*.$ This shows that if you move away from any point in ${{ \mathbb{R}}}$ for sufficiently large $t$ with speed $c$ that is higher than the minimal speed $c^*,$ then you would be able to outrun the infected population. However, the infected population will surpass you if $c < c^*.$

The basic reproduction number has been calculated to be between 2 and 3.58 [20,22,24,25,27,28,30,31,32,42,44,46]. The calculated range of ${{\mathcal R}}_0$ means that one patient could infect two to three other people [42]. We can reach the following conclusions by Table 2. First, the range ${{\mathcal R}}_0 \in[2, 3.58]$ suggests that the density of susceptible individuals $S_0$ available to be infected is from approximately $2 \ [ \rm{people}/ \rm{km}^2]$ to $4 \ [ \rm{people}/ \rm{km}^2]$. In addition, $S_0$ greatly impacts the value of the basic reproduction number ${{\mathcal R}}_0$. Quarantining part of the infectious population can effectively reduce the value of ${{\mathcal R}}_0$ as demonstrated by Table 2. This clearly shows that population density and quarantine play crucial roles in the spreading speed of COVID-19.

We conclude this work by pointing out some of the limitations of the model and future study. The model assumes that the recovered individuals are immune to the disease. Hence, the resulting system is a susceptible-exposed(infected)-infectious-recovered (SEIR) mathematical model. However, allowing recovered people to return to the susceptible stage seems reasonable biologically. With this assumption, we would have a more complex mathematical model. This fact compels us to extend this work in the future by studying the SEIRS version of this model.

Use of AI tools declaration

The authors declares he has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author extends his appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA, for funding this research work through the project number NBU-FPEJ-2024-133-01.

Conflict of interest

The author declares no conflict of interest.