Synchronization of Clifford-valued neural networks with leakage, time-varying, and infinite distributed delays on time scales

1.   Introduction

Recently, neural networks (NNs) defined on multidimensional domains have been considered as an extension of real-valued neural networks (RVNNs). As such, complex-valued neural networks (CVNNs), for which the domain is the 2D complex numbers algebra, and quaternion-valued neural networks (QVNNs), for which the domain is the 4D quaternion algebra, were introduced and different dynamic properties were studied for them. Then, they were generalized to Clifford-valued neural networks (ClVNNs), for which the domain can be any $2^{n}$-dimensional Clifford algebra, with $n\geq1$.

ClVNNs were first introduced, in their feedforward variant, in ^[1]. Then, in their recurrent Hopfield variant, ClVNNs were introduced in ^[2]. Because of their generality, it is expected that ClVNNs will have applications in problems related to high-dimensional data processing and analysis.

Starting from paper ^[3], different dynamic properties have been researched for recurrent ClVNNs, such as stability ^{[4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]}, synchronization ^{[15, 16]}, fixed/finite-time synchronization ^{[17, 18, 19]}, dissipativity ^[20], etc.

The finite reaction time of circuit components causes time delays in real-world NN implementations, which may result in undesirable behavior. Time delays must thus be incorporated into the models that are used to analyze the dynamic properties of NNs ^{[21, 22, 23]}. One type of delay, which appears in the self-feedback term of NNs, is the leakage delay, and it has been discussed, in the context of ClVNNs, in ^{[5, 6, 13, 16, 24, 25, 26, 27]}. Then, the dispersion of conduction speeds throughout an NN's implementation pathways may give rise to distributed delays. Finite distributed delays are the most common types of distributed delays, which were added to models of ClVNNs in ^{[14, 17, 18]}. They are called mixed delays when they appear in conjunction with time-varying delays and were considered as part of ClVNN models in ^{[20, 28, 29]}. However, infinite distributed delays have been more rarely discussed in the literature concerning NNs in general, and, for ClVNNs, were only present as a part of the model in ^[18], to our awareness.

On the other hand, the majority of the papers involving the study of the dynamics of NNs in general are done in continuous time. Nonetheless, when implementing NNs in circuits, discretization is a necessary step, and it's possible that the dynamics of the discrete time model differs from that of its continuous time counterpart. This observation led to the idea of discussing NNs directly in discrete time for the first time in ^[30]. Discrete time NNs have since then become a topic in their own right, attracting more and more research avenues with the passing of time. To the best of our knowledge, discrete time ClVNNs have not been yet discussed in the available scientific literature.

A method to unify the study of continuous and discrete time systems, or any hybrid combination of them, has been put forward in the form of time scale calculus, which was developed for the first time in ^[31]. Time scale calculus was later expanded and summarized in the books ^{[32, 33, 34]}, which represent important references for further developments regarding time scales. Time scales were also added to the study of NNs for the first time in ^[35]. Since then, time scale NNs have also become an increasingly popular field of study. ClVNNs defined on time scales were the focus of ^{[15, 24, 26]}.

Since time scale calculus is more general and has to encompass the characteristics of both differential and difference systems, the classical Lyapunov theory is not applicable for systems defined on time scales. Alternatively, Halanay inequalities have been used to study the dynamics of such systems. Different types of Halanay inequalities have been proposed over time; see ^{[36, 37, 38, 39, 40]}. These inequalities have also been extended to time scales, yielding Halanay inequalities for time scales (see ^{[41, 42, 43, 44]}), which have been used to study the dynamics of NNs defined on time scales, for example, in ^{[45, 46, 47, 48, 49, 50, 51]}.

Considering all the above observations, this paper has the subsequent key contributions:

1. A very general model of ClVNNs defined on time scales is put forward, encompassing leakage, time-varying, and infinite distributed delays, which were rarely present in the literature.

2. Two types of Lyapunov-like functions are defined, which allow the application of a Halanay inequality on time scales.

3. Based on these functions, sufficient conditions expressed as algebraic inequalities and linear matrix inequalities (LMIs) which ensure the exponential synchronization of the proposed model are formulated, using a general state feedback control scheme.

4. One numerical example is provided for each of the two theorems, both in the discrete and continuous time contexts.

5. The proposed model is so general that it is possible to particularize it for discrete time or continuous time ClVNNs, or even for CVNNs or QVNNs, for which no comparable results have been reported in the literature, to our awareness.

The remaining part of the paper has the following organization. The presentation of the Clifford algebras, the basics of time scale calculus, the discussed model and its transformation to a real-valued one, and the necessary assumptions and lemmas all together form Section 2. Afterward, in Section 3, two kinds of Lyapunov-like functions are used in order to obtain sufficient conditions expressed as algebraic inequalities and LMIs, respectively, which ensure the exponential synchronization of the proposed NNs, based on a state feedback control scheme. Two numerical examples are put forward in Section 4 to illustrate the results presented in the previous section. Finally, Section 5 draws the conclusions of the present research.

Notations: $\mathbb{R}$ – reals, $\mathbb{R}^{+}$ – positive reals, $\mathcal{C\ell}_{p, q}$ – Clifford algebra, $\mathbb{R}^{N}$ ($\mathcal{C\ell}_{p, q}^{N}$) – real (Clifford) vectors of dimension $N$, $\mathbb{R}^{N\times N}$ ($\mathcal{C\ell}_{p, q}^{N\times N}$) – real (Clifford) $N\times N$-dimensional matrices, $\lambda_{\text{min}}(A)$ – smallest eigenvalue of $A$, $A^{T}$ – transpose of $A$, $A < 0$ – $A$ is negative definite, $||\cdot||_{p}$ – $L_{p}$ norm, $p\in\{1, 2\}$.

2.   Preliminaries

We begin by introducing Clifford algebras. Let $\{e_{1}, \ldots, e_{n}\}$ be an orthonormal basis of $\mathbb{R}^{n}$, where $n\geq1$. Let $p, q\in\{0, \ldots, n\}$ with $n = p+q$, and define the operation $\otimes_{p, q}$ as:

Define

where $\mathcal{P}(\{1, \ldots, n\})$ is the power set, i.e., the set of all subsets, of $\{1, \ldots, n\}$.

For any $I\in\mathcal{I}$, we define:

Particularly, $e_{\emptyset} = 1_{\mathbb{R}}$. In what follows, when there is no danger of confusion, we will denote $e_{I} = e_{\{i_{1}, \ldots, i_{s}\}}$ with $e_{i_{1}\cdots i_{s}}$.

With these notations, the Clifford number set $\mathcal{C\ell}_{p, q}$ is defined as:

It can be proved that, together with the operation $\otimes_{p, q}$, defined above, $\mathcal{C\ell}_{p, q}$ represents an associative real algebra of dimension $2^{n}$, called a Clifford algebra.

For each Clifford number $x\in\mathcal{C\ell}_{p, q}$, its conjugate is defined as $\overline{x}: = \sum_{I\in\mathcal{I}}x^{I}\overline{e}_{I}$, where $\overline{e}_{I} = (-1)^{\frac{|I|(|I|+1)}{2}}e_{I}$, and $|I|$ denotes the cardinality of set $I$. Then, we define the norm of Clifford number $x\in\mathcal{C\ell}_{p, q}$ as $|x|_{\mathcal{C\ell}_{p, q}}: = \sqrt{\overline{x}\otimes_{p, q}x} = \sqrt{\sum_{I\in\mathcal{I}}(x^{I})^{2}}$.

On the other hand, we give a basic introduction to time scale calculus mainly based on ^[32]. "A nonempty closed subset of the real number set $\mathbb{R}$, from which the topology and ordering are inherited, is called a time scale $\mathbb{T}$. $\forall t\in\mathbb{T}$, the forward jump operator is defined as $\sigma(t): = \inf\{\left.s\in\mathbb{T}\right|s > t\}$, and the backward jump operator as $\rho(t) = \sup\{\left.s\in\mathbb{T}\right|s < t\}$. The forward graininess function is defined as $\mu:\mathbb{T}\to[0, +\infty)$, $\mu(t): = \sigma(t)-t$, $\forall t\in\mathbb{T}$. Also, put $\hat{\mu} = \sup\{\left.\mu(t)\right|t\in\mathbb{T}\}$.

Once this is established, a point $t\in\mathbb{T}$ is right (left)-dense if $\sigma(t) = t$ ($\rho(t) = t$) and right (left)-scattered if $\sigma(t) > t$ ($\rho(t) < t$). $\mathbb{T}^{\kappa}: = \mathbb{T}\backslash\{m\}$, where $m$ is the left-scattered maximum of $\mathbb{T}$, if it exists, otherwise $\mathbb{T}^{\kappa}: = \mathbb{T}$. If $f(t_{1}) = \lim_{\zeta\to t_{1}^{+}}f(\zeta)$ for any right-dense $t_{1}\in\mathbb{T}$, and $\lim_{\zeta\to t_{2}^{-}}f(\zeta)$ exists for any left-dense $t_{2}\in\mathbb{T}$, then the function $f:\mathbb{T}\to\mathbb{R}$ is called rd-continuous. $C_{rd}(\mathbb{T}, \mathbb{R})$ designates the set of all functions $f:\mathbb{T}\to\mathbb{R}$ which are rd-continuous. The jump operators are defined as $f^{\sigma}(t) = f(\sigma(t))$ and $f^{\rho}(t) = f(\rho(t))$, respectively, for a function $f:\mathbb{T}\to\mathbb{R}$. If $p\in C_{rd}(\mathbb{T}, \mathbb{R})$ and $1+\mu(t)p(t)\neq0$, $\forall t\in\mathbb{T}^{\kappa}$, then function $p:\mathbb{T}\to\mathbb{R}$ is said to be regressive, and we denote by $\mathcal{R}(\mathbb{T}, \mathbb{R})$ the set of all regressive functions. The set $\mathcal{R}^{+}(\mathbb{T}, \mathbb{R})$ denotes all positively regressive functions, which are functions $p:\mathbb{T}\to\mathbb{R}$ for which $p\in C_{rd}(\mathbb{T}, \mathbb{R})$ and $1+\mu(t)p(t) > 0$, $\forall t\in\mathbb{T}^{\kappa}$. We establish the following formula: $\forall p\in\mathcal{R}(\mathbb{T}, \mathbb{R})$, $\ominus p(t): = -p(t)/(1+\mu(t)p(t))$, $\forall t\in\mathbb{T}$. For any set $S\subseteq\mathbb{R}$, we define $S_{\mathbb{T}} = S\cap\mathbb{T}$.

Given a function $f:\mathbb{T}\to\mathbb{R}$, the number denoted by $f^{\Delta}(t)$ for $t\in\mathbb{T}^{\kappa}$ such that $\forall\varepsilon > 0$, there exists a $\delta > 0$ so that the subsequent inequality is valid $\forall s\in(t-\delta, t+\delta)_{\mathbb{T}}$:

represents, if it exists, the $\Delta$-derivative of $f$ at $t$. The function $f$ is said to be $\Delta$-differentiable if the $\Delta$-derivative exists $\forall t\in\mathbb{T}^{\kappa}$.

The inverse operation of $\Delta$-differentiation is $\Delta$-integration, i.e., if $F^{\Delta}(t) = f(t)$, then

Lastly, for any regressive function $p\in\mathcal{R}(\mathbb{T}, \mathbb{R})$, the $\Delta$-exponential function $e_{p}:\mathbb{T}\times\mathbb{T}\to\mathbb{R}$ is defined by the formula:

where $\xi_{\mu(s)}$ represents the cylinder transformation, given as:

Define the following ClVNN with leakage, time-varying, and infinite distributed delays on time scale $\mathbb{T}$, which will serve as the drive system:

$\forall i\in\{1, \ldots, N\}$, $\forall t\in[0, +\infty)_{\mathbb{T}}$, where $x(t) = (x_{1}(t), \ldots, x_{N}(t))^{T}\in\mathcal{C\ell}_{p, q}^{N}$ represents the vector of states at $t\in[0, +\infty)_{\mathbb{T}}$, $C = \text{diag}(c_{1}, \ldots, c_{N})\in\mathbb{R}^{N\times N}$ (with $c_{i} > 0$, $\forall i\in\{1, \ldots, N\}$) represents the self-feedback weight matrix, $A = (a_{ij})_{1\leq i, j\leq N}\in\mathcal{C\ell}_{p, q}^{N\times N}$ is the weight matrix without delay, $B = (b_{ij})_{1\leq i, j\leq N}\in\mathcal{C\ell}_{p, q}^{N\times N}$ is the weight matrix with delay, $G = (g_{ij})_{1\leq i, j\leq N}\in\mathcal{C\ell}_{p, q}^{N\times N}$ is the infinite distributed delay weight matrix, $K:[0, +\infty)_{\mathbb{T}}\to\mathbb{R}$ is the infinite distributed delay kernel function, $f_{j}:\mathcal{C\ell}_{p, q}\to\mathcal{C\ell}_{p, q}$ represent the activation functions, $\forall j\in\{1, \ldots, N\}$, and $E = (E_{1}, \ldots, E_{N})^{T}\in\mathcal{C\ell}_{p, q}^{N}$ is the external inputs vector. The time-varying delays are $\sigma:[0, +\infty)_{\mathbb{T}}\to[0, +\infty)_{\mathbb{T}}$. Assume that there exists $\sigma\in(0, +\infty)_{\mathbb{T}}$ with $\sigma(t)\leq\sigma$, $\forall t\in[0, +\infty)_{\mathbb{T}}$, and the leakage delay is $\gamma\in[0, +\infty)_{\mathbb{T}}$. The notation $\varphi: = \max\{\gamma, \sigma\}$ is made. Also, assume that the activation functions $f_{j}$ have the form $f_{j}(x) = \sum_{I\in\mathcal{I}}f_{j}^{I}(x)e_{I}$, $\forall x\in\mathcal{C\ell}_{p, q}$, where $f_{j}^{I}:\mathcal{C\ell}_{p, q}\to\mathbb{R}$, $\forall j\in\{1, \ldots, N\}$, $\forall I\in\mathcal{I}$.

For NN (1), the initial conditions are expressed as:

where $\psi_{i}\in\mathcal{C}([-\varphi, 0]_{\mathbb{T}}, \mathcal{C\ell}_{p, q})$, $\forall i\in\{1, \ldots, N\}$. On set $\mathcal{C}([-\varphi, 0]_{\mathbb{T}}, \mathcal{C\ell}_{p, q}^{N})$, the norm is defined as $||\psi||: = \sum_{i = 1}^{N}\sup_{[-\varphi, 0]_{\mathbb{T}}}|\psi_{i}(t)|$.

The response NN, which is needed in order to analyze synchronization, will correspondingly be defined as:

$\forall i\in\{1, \ldots, N\}$, $\forall t\in[0, +\infty)_{\mathbb{T}}$; $y(t) = (y_{1}(t), \ldots, y_{N}(t))^{T}\in\mathcal{C\ell}_{p, q}^{N}$ is the state vector at $t\in[0, +\infty)_{\mathbb{T}}$; and $u(t) = (u_{1}(t), \ldots, u_{N}(t))^{T}\in\mathcal{C\ell}_{p, q}^{N}$ is the vector of control inputs at $t\in[0, +\infty)_{\mathbb{T}}$.

The NN (2) has its initial conditions defined as:

where $\phi_{i}\in\mathcal{C}([-\varphi, 0]_{\mathbb{T}}, \mathcal{C\ell}_{p, q})$, $\forall i\in\{1, \ldots, N\}$.

Taking into account relations (1) and (2), and denoting $\mathfrak{z}_{i}(t) = y_{i}(t)-x_{i}(t)$, $\forall i\in\{1, \ldots, N\}$, $\forall t\in[0, +\infty)_{\mathbb{T}}$, the error system will have the following expression:

$\forall i\in\{1, \ldots, N\}$, $\forall t\in[0, +\infty)_{\mathbb{T}}$, where $\tilde{f}_{j}(\mathfrak{z}_{j}(t)) = f_{j}(\mathfrak{z}_{j}(t)+x_{j}(t))-f_{j}(x_{j}(t))$, $\forall t\in[0, +\infty)_{\mathbb{T}}$, $\forall j\in\{1, \ldots, N\}$.

Now, NN (3) will have the initial conditions expressed as:

where $\chi_{i}\in\mathcal{C}([-\varphi, 0]_{\mathbb{T}}, \mathcal{C\ell}_{p, q})$, $\forall i\in\{1, \ldots, N\}$.

Taking into account that $\forall K, I\in\mathcal{I}$, $\exists J\in\mathcal{I}$, such that $e_{K} = (-1)^{\rho[I\cdot\overline{J}]}e_{I}\otimes_{p, q}\overline{e}_{J}$, where $\rho[I\cdot\overline{J}] = \begin{cases} 0, & e_{K} = e_{I}\otimes_{p, q}\overline{e}_{J}\\ 1, & e_{K} = -e_{I}\otimes_{p, q}\overline{e}_{J} \end{cases}$, and, if we denote $x^{I\cdot\overline{J}}: = (-1)^{\sigma[I\cdot\overline{J}]}x^{K}$, we have that $x^{K}e_{K} = x^{I\cdot\overline{J}}e_{I}\otimes_{p, q}\overline{e}_{J}$, and system (3) can be equivalently written as:

The system of equations (3) will now be converted into $2^{n}$ real-valued systems. This is accomplished by using the following $2^{n}$ equations to represent each equation in (3), based on relation (4):

$\forall I\in\mathcal{I}$, $\forall i\in\{1, \ldots, N\}$.

If we now denote:

and $\text{vec}(x): = ((x^{I})_{I\in\mathcal{I}})^{T}\in\mathbb{R}^{2^{n}}$, the expression of system (3) will be the following:

$\forall i\in\{1, \ldots, N\}$, $\forall t\in[0, +\infty)_{\mathbb{T}}$.

Lastly, if we make the following notations:

the expression of system (3) will be:

We have to make the following assumptions:

Assumption 1. (^[52]) "The activation functions $f_{j}$ satisfy $\forall x, \ x'\in\mathcal{C\ell}_{p, q}$, the following Lipschitz conditions:

$\forall I\in\mathcal{I}$, $\forall j\in\{1, \ldots, N\}$, where $l_{j}^{I} > 0$ represent the Lipschitz constants. Furthermore, we denote $\check{L}: = \mathit{\text{diag}}((l_{1}^{I})_{I\in\mathcal{I}}, \ldots, (l_{N}^{I})_{I\in\mathcal{I}})\in\mathbb{R}^{2^{n}N\times2^{n}N}$."

Assumption 2. The infinite distributed delay kernel function $K:[0, +\infty)_{\mathbb{T}}\to\mathbb{R}$ satisfies:

We will also need the following lemmas regarding time scales in order to conduct the proofs of our theorems:

Lemma 1. (^[32]) "If $f, g:\mathbb{T}\to\mathbb{R}$ are $\Delta$-differentiable, then

(i) $(f(t)+g(t))^{\Delta} = f^{\Delta}(t)+g^{\Delta}(t)$;

(ii) $(f(t)g(t))^{\Delta} = f^{\Delta}(t)g(t)+f(\sigma(t))g^{\Delta}(t) =$ $f(t)g^{\Delta}(t)+f^{\Delta}(t)g(\sigma(t)).$"

Lemma 2. (^[51]) "Let $y(t)$ be a nonnegative rd-continuous function on $\mathbb{T}$, and

holds for $t\in[t_{0}, +\infty)_{\mathbb{T}}$, $t_{0}$, $t-s\in\mathbb{T}$, where $\alpha_{1}$, $\alpha_{2}$, $\alpha_{3}$ , and $\beta$ are four positive constants, $K(s)\geq0$ holds for $s\in[0, \infty)_{\mathbb{T}}$, and $\int_{0}^{\infty}K(s)e^{s}\Delta s<\infty$. If $-\alpha_{1}\in\mathcal{R}^{+}$, $\alpha_{1}>\alpha_{2}+\alpha_{3}\int_{0}^{\infty}K(s)\Delta s$, then

for any $t\in[t_{0}, +\infty)_{\mathbb{T}}$, where $\gamma = \beta/(\alpha_{1}-\alpha_{2}-\alpha_{3}\int_{0}^{\infty}K(s)\Delta s)$, $\lambda > 0$ satisfies the inequality

Lemma 3. (^[51]) "Suppose that $x(t)\in\mathbb{R}^{n}$ is rd-continuous and $f(\cdot)\in C_{rd}$ is a $\Delta$-differentiable convex function. If $\int_{0}^{\infty}K(s)\Delta s = 1$, then

holds for $\forall t\in\mathbb{T}$, where $K(s)\geq0$ holds for $s\in[0, \infty)_{\mathbb{T}}$."

Lemma 4. (^[46]) "If $-\lambda\in\mathcal{R}^{+}$, $y\in C_{rd}(\mathbb{T}, \mathbb{R})$, $z\in C_{rd}(\mathbb{T}, \mathbb{R})$, then $\forall t\in\mathbb{T}$,

implies

3.   Main results

In order to realize synchronization between drive system (1) and response system (2), we design the following state feedback controller:

in which the real positive diagonal matrices $K_{1}, \ldots, K_{4}\in\mathbb{R}^{N\times N}$ are the control gain matrices. By incorporating this controller, system (5) becomes:

where $\check{K}_{1}: = \text{diag}(k_{11}I_{2^{n}}, k_{21}I_{2^{n}}, \ldots, k_{N1}I_{2^{n}})\in\mathbb{R}^{2^{n}N\times2^{n}N}$, $\check{K}_{2}: = \text{diag}(k_{12}I_{2^{n}}, k_{22}I_{2^{n}}, \ldots, k_{N2}I_{2^{n}})\in\mathbb{R}^{2^{n}N\times2^{n}N}$, $\check{K}_{3}: = \text{diag}(k_{13}I_{2^{n}}, k_{23}I_{2^{n}}, \ldots, k_{N3}I_{2^{n}})\in\mathbb{R}^{2^{n}N\times2^{n}N}$, $\check{K}_{4}: = \text{diag}(k_{14}I_{2^{n}}, k_{24}I_{2^{n}}, \ldots, k_{N4}I_{2^{n}})\in\mathbb{R}^{2^{n}N\times2^{n}N}$.

Theorem 1. Drive NN (1) is exponentially synchronized with response NN (2) under control scheme (6) if Assumptions 1 and 2 are satisfied and the subsequent LMIs are true:

where $\Omega_{1, 1} = -P\check{K}_{1}-\check{K}_{1}P+(\hat{\mu}+\alpha_{1})P+\check{L}^{T}R_{1}\check{L}-N_{2}\check{K}_{1}-\check{K}_{1}N_{2}^{T}$, $\Omega_{1, 2} = -N_{2}-\check{K}_{1}N_{1}^{T}$, $\Omega_{1, 3} = -P(\check{C}+\check{K}_{2})-N_{2}(\check{C}+\check{K}_{2})-\check{K}_{1}N_{3}^{T}$, $\Omega_{1, 4} = -P\check{K}_{3}-N_{2}\check{K}_{3}-\check{K}_{1}N_{4}^{T}$, $\Omega_{1, 5} = P\check{A}+N_{2}\check{A}+\check{K}_{1}N_{6}^{T}$, $\Omega_{1, 6} = P\check{B}+N_{2}\check{B}+\check{K}_{1}N_{7}^{T}$, $\Omega_{1, 7} = -P\check{K}_{4}-N_{2}\check{K}_{4}-\check{K}_{1}N_{5}^{T}$, $\Omega_{1, 8} = P\check{G}+N_{2}\check{G}+\check{K}_{1}N_{8}^{T}$, $\Omega_{2, 2} = -N_{1}-N_{1}^{T}$, $\Omega_{2, 3} = -N_{1}(\check{C}+\check{K}_{2})-N_{3}^{T}$, $\Omega_{2, 4} = -N_{1}\check{K}_{3}-N_{4}^{T}$, $\Omega_{2, 5} = N_{1}\check{A}+N_{6}^{T}$, $\Omega_{2, 6} = N_{1}\check{B}+N_{7}^{T}$, $\Omega_{2, 7} = -N_{1}\check{K}_{4}-N_{5}^{T}$, $\Omega_{2, 8} = N_{1}\check{G}+N_{8}^{T}$, $\Omega_{3, 3} = -N_{3}(\check{C}+\check{K}_{2})-(\check{C}+\check{K}_{2})N_{3}^{T}-\alpha_{21}P$, $\Omega_{3, 4} = -N_{3}\check{K}_{3}-(\check{C}+\check{K}_{2})N_{4}^{T}$, $\Omega_{3, 5} = N_{3}\check{A}+(\check{C}+\check{K}_{2})N_{6}^{T}$, $\Omega_{3, 6} = N_{3}\check{B}+(\check{C}+\check{K}_{2})N_{7}^{T}$, $\Omega_{3, 7} = -N_{3}\check{K}_{4}-(\check{C}+\check{K}_{2})N_{5}^{T}$, $\Omega_{3, 8} = N_{3}\check{G}+(\check{C}+\check{K}_{2})N_{8}^{T}$, $\Omega_{4, 4} = \check{L}^{T}R_{2}\check{L}-N_{4}\check{K}_{3}-\check{K}_{3}N_{4}^{T}-\alpha_{22}P$, $\Omega_{4, 5} = N_{4}\check{A}+\check{K}_{3}N_{6}^{T}$, $\Omega_{4, 6} = N_{4}\check{B}+\check{K}_{3}N_{7}^{T}$, $\Omega_{4, 7} = -N_{4}\check{K}_{4}-\check{K}_{3}N_{5}^{T}$, $\Omega_{4, 8} = N_{4}\check{G}+\check{K}_{3}N_{8}^{T}$, $\Omega_{5, 5} = -N_{6}\check{A}-\check{A}^{T}N_{6}^{T}-R_{1}$, $\Omega_{5, 6} = -N_{6}\check{B}-\check{A}^{T}N_{7}^{T}$, $\Omega_{5, 7} = \check{A}^{T}N_{5}^{T}+N_{6}\check{K}_{4}$, $\Omega_{5, 8} = -N_{6}\check{G}-\check{A}^{T}N_{8}^{T}$, $\Omega_{6, 6} = -R_{2}-N_{7}\check{B}-\check{B}^{T}N_{7}^{T}$, $\Omega_{6, 7} = \check{B}^{T}N_{5}^{T}+N_{7}\check{K}_{4}$, $\Omega_{6, 8} = -N_{7}\check{G}-\check{B}^{T}N_{8}^{T}$, $\Omega_{7, 7} = -N_{5}\check{K}_{4}-\check{K}_{4}N_{5}^{T}$, $\Omega_{7, 8} = N_{5}\check{G}+\check{K}_{4}N_{8}^{T}$, $\Omega_{8, 8} = -R_{3}-N_{8}\check{G}-\check{G}^{T}N_{8}^{T}$, matrix $P\in\mathbb{R}^{2^{n}N\times2^{n}N}$ is positive definite, matrices $R_{1}, \; R_{2}, \; R_{3}\in\mathbb{R}^{2^{n}N\times2^{n}N}$ are diagonal positive definite, $N_{1}, \ldots, N_{8}\in\mathbb{R}^{2^{n}N\times2^{n}N}$ are any matrices, and real positive numbers $\alpha_{1}, \; \alpha_{21}, \; \alpha_{22}, \; \alpha_{3}$ satisfy $-\alpha_{1}\in\mathcal{R}^{+}$ and

Proof. We start by putting forward the subsequent Lyapunov-like function:

Taking into account Lemma 1 and the expression of system (7), the $\Delta$-derivative of $V$ for the positive half trajectory of system (7) has the following expression:

On the other hand, Assumption 1 guarantees the existence of diagonal positive definite matrices $R_{1}, R_{2}\in\mathbb{R}^{2^{n}N\times2^{n}N}$ such that $\forall t\in[0, +\infty)_{\mathbb{T}}$:

Also, from Lemma 3 and Assumption 1, we get that there exists positive definite matrix $R_{3}\in\mathbb{R}^{2^{n}N\times2^{n}N}$ such that $\forall t\in[0, +\infty)_{\mathbb{T}}$:

Moreover, for any matrices $N_{1}, \ldots, N_{8}\in\mathcal{C\ell}_{p, q}^{N\times N}$, the next identity is true:

Now, in Lemma 2, we take $\forall t\in[0, +\infty)_{\mathbb{T}}$:

and, using relations (9)–(13), we have that:

where, for the last inequality, we used the hypotheses (8) and

This means that the first inequality in Lemma 2 holds.

From the hypothesis of the theorem, we have that the second inequality in Lemma 2 is also true, which means that we can apply Lemma 2 to obtain:

or, equivalently,

which shows that drive NN (1) is exponentially synchronized with response NN (2) under control scheme (6), exactly what we wanted to prove. □

Theorem 2. Provided that positive numbers $\omega_{i}$, $0\leq i\leq2^{n}N$, exist, the following inequality is true:

and $-\alpha_{1}\in\mathcal{R}^{+}$, where

$\alpha_{1} = \min_{1\leq i\leq2^{n}N}\left\{ \check{k}_{1i}-\sum_{j = 1}^{2^{n}N}|\check{a}_{ji}|\frac{\omega_{j}}{\omega_{i}}\check{l}_{i}\right\}$,

$\alpha_{2} = \max_{1\leq i\leq2^{n}N}\left\{ \check{c}_{i}+\check{k}_{2i}+\check{k}_{3i}+\sum_{j = 1}^{2^{n}N}|\check{b}_{ji}|\frac{\omega_{j}}{\omega_{i}}\check{l}_{i}\right\}$,

$\alpha_{3} = \max_{1\leq i\leq2^{n}N}\left\{ \check{k}_{4i}+\sum_{j = 1}^{2^{n}N}|\check{g}_{ji}|\frac{\omega_{j}}{\omega_{i}}\check{l}_{i}\right\}$,

and, also, Assumptions 1 and 2 are satisfied, then drive NN (1) is exponentially synchronized with response NN (2) under state feedback controller (6).

Proof. The following Lyapunov-like function is put forward:

For the positive half trajectory of system (7), employing Lemma 4, the $\Delta$-derivative of $V$ has the following explicitation:

At this point, in Lemma 2, we take

Now, relation (14) allows us to write $\forall t\in[0, +\infty)_{\mathbb{T}}$, that:

where $\alpha_{1}$, $\alpha_{2}$, $\alpha_{3}$ are given in the hypothesis of the theorem. This means that the first inequality in Lemma 2 holds. The second inequality in Lemma 2 also holds, based on the hypothesis of the theorem.

Thus, we can apply Lemma 2, which gives:

which is equivalent with:

meaning that drive NN (2) is exponentially synchronized with response NN (3) under state feedback controller (6), precisely what we had to prove. □

4.   Numerical examples

Example 1. For the first example, consider the time scale $\mathbb{T} = 0.1\mathbb{Z}$, from which we get that $\hat{\mu} = 0.1$.

Also, consider that the NNs are defined on the 8D Clifford algebra $\mathcal{C\ell}_{0, 3}$, which has the following multiplication table:

Consider the subsequent ClVNN with two neurons, with leakage, time-varying, and infinitely distributed delays defined on time scale $\mathbb{T}$ as the drive system:

and the corresponding response system:

$\forall i\in\{1, 2\}$, $\forall t\in[0, \infty)_{\mathbb{T}}$.

Taking into account relations (15) and (16) and denoting $\mathfrak{z}_{i}(t) = y_{i}(t)-x_{i}(t)$, $\forall i\in\{1, 2\}$, $\forall t\in[0, +\infty)_{\mathbb{T}}$, the error system will have the following expression:

$\forall i\in\{1, 2\}$, $\forall t\in[0, +\infty)_{\mathbb{T}}$, and $\tilde{f}_{j}(\mathfrak{z}_{j}(t)) = f_{j}(\mathfrak{z}_{j}(t)+x_{j}(t))-f_{j}(x_{j}(t))$, $\forall t\in[0, +\infty)_{\mathbb{T}}$, $\forall j\in\{1, 2\}$.

In order to achieve synchronization between drive system (15) and response system (16), we design the following controller of state feedback type:

where the real positive diagonal matrices $K_{1}, \ldots, K_{4}\in\mathbb{R}^{2\times2}$ are the control gain matrices. Using this control scheme, NN (17) can be equivalently written as:

The parameters of the model are:

which allows us to conclude that $L = \begin{bmatrix}0.25 & 0\\ 0 & 0.25 \end{bmatrix}$, meaning that Assumption 1 is satisfied.

The time-varying delays are $\sigma(t) = 0.9|\cos t|$ and the leakage delay is $\gamma = 0.7$, which means that $\sigma = 0.9$ and $\varphi = \max\{\sigma, \gamma\} = 0.9$. The infinite distributed delay kernel function is given by $K(s) = 2e_{2}(0, s)$, $\forall s\in[0, \infty)_{\mathbb{T}}$, which it can be easily verified that it satisfies Assumption 2.

The control gain matrices are designed as:

Also, we take $\alpha_{1} = 5.1$, $\alpha_{21} = 1$, $\alpha_{22} = 2$, $\alpha_{3} = 2$, which satisfy $\alpha_{1} > \alpha_{21}+\alpha_{22}+\alpha_{3}\int_{0}^{\infty}K(s)\Delta s$ and $-\alpha_{1}\in\mathcal{R}^{+}$. Taking all of the above into consideration, we can conclude that all the conditions of Theorem 1 are met and the LMIs in (8) are solved to give $R_{1} = \text{diag}(1.1976I_{8}, 1.2841I_{8})$, $R_{2} = \text{diag}(1.3380I_{8}, 1.3591I_{8})$, $R_{3} = \text{diag}(1.0237I_{8}, 1.0259I_{8})$, (the values of the other matrices are omitted so as not to clutter the paper), which allows us to reach the conclusion that drive NN (15) is exponentially synchronized with response NN (16) under control scheme (18).

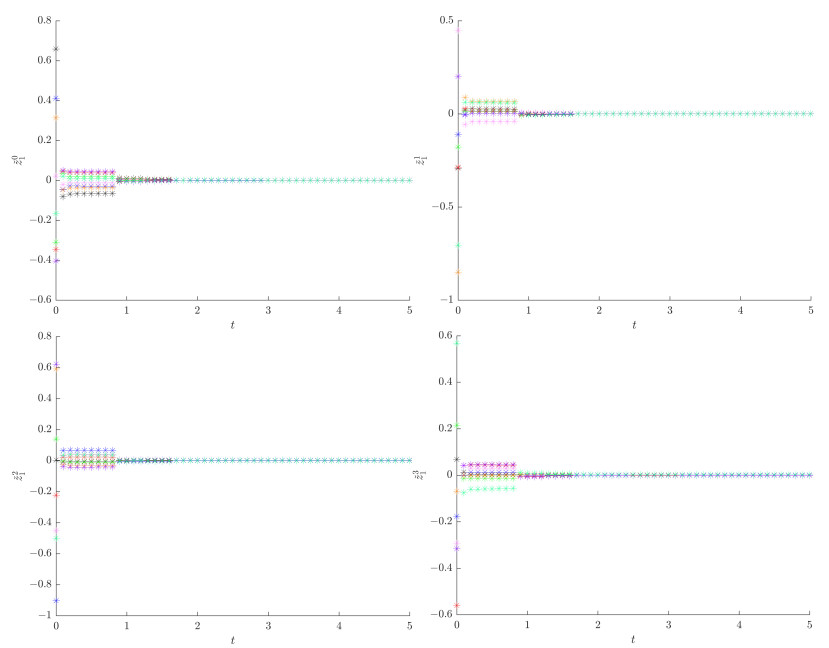
Figures 1 (a), 1 (b), 2 (a), 2 (b) depict the Clifford components of the state trajectories of $\check{\mathfrak{z}}_{1}$ and $\check{\mathfrak{z}}_{2}$, starting from $8$ initial values.

Example 2. Now, consider the time scale $\mathbb{T} = \mathbb{R}$, which means that $\hat{\mu} = 0$. Also, take the same systems (15) and (16) and the same controller (18), defined on the same 8D algebra $\mathcal{C\ell}_{0, 3}$, but with the following parameters:

which allows us to conclude that $L = \begin{bmatrix}0.25 & 0\\ 0 & 0.25 \end{bmatrix}$, meaning that Assumption 1 is satisfied.

The time-varying delays are $\sigma(t) = 0.8|\sin t|$ and the leakage delay is $\gamma = 0.6$, which means that $\sigma = 0.8$ and $\varphi = \max\{\sigma, \gamma\} = 0.8$. The infinite distributed delay kernel function is given by $K(s) = 2e^{-2s}$, $\forall s\in[0, \infty)_{\mathbb{T}}$, which it can be easily verified that it satisfies Assumption 2.

The control gain matrices are designed as:

Also, we compute $\alpha_{1} = 6.9750$, $\alpha_{2} = 3.1750$, $\alpha_{3} = 3$, which satisfy $-\alpha_{1}\in\mathcal{R}^{+}$ and $\alpha_{1}-\alpha_{2}-\alpha_{3}\int_{0}^{\infty}K(s)\Delta s = 0.8 > 0$. All the conditions of Theorem 2 are met, which allows us to reach the conclusion that drive NN (15) is exponentially synchronized with response NN (16) under control scheme (18), with the above-defined parameters.

Figures 3 (a), 3 (b), 4 (a), 4 (b) depict the Clifford components of the state trajectories of $\check{\mathfrak{z}}_{1}$ and $\check{\mathfrak{z}}_{2}$, starting from $8$ initial points.

5.   Conclusions

The aim of this paper was to present a general model of ClVNNs defined on time scales, encompassing leakage, time-varying, and infinite distributed delays, which were rarely added to NN models in the existing literature. A Halanay inequality for time scales was used together with Lyapunov-like functions of two types in order to deduce sufficient conditions expressed as algebraic inequalities and as LMIs for the exponential synchronization of the model put forward, on the basis of a general state feedback control scheme. Numerical examples defined both in discrete time and continuous time were put forward to illustrate the obtained theoretical results.

The theorems presented in the paper are general enough that they can be particularized for both continuous time and discrete time ClVNNs, or any hybrid combination of the two. They can also be particularized for CVNNs or QVNNs, for which the respective results are not present in the available literature, to our awareness. Also, the methods used in the paper can be employed to deduce sufficient criteria for other dynamic properties, such as stability, dissipativity, passivity, etc., for other types of models defined on time scales, for instance, for NNs with Markov jump parameters, inertial terms, impulsive effects, or reaction–diffusion terms. These represent promising avenues for future works.

Acknowledgment

This work is supported by a grant of the Ministry of Research, Innovation and Digitization, CNCS-UEFISCDI, project number PN-Ⅲ-P1-1.1-PD-2021-0345, within PNCDI Ⅲ.

Use of AI tools declaration

The author declares that he has not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The author declares that there is no conflict of interest.