A new hybrid classification algorithm for predicting student performance

1.   Introduction

Educational institutions globally are constantly innovating to uncover strategies that not only foresee but also boost student achievements, laying the groundwork for a future where academic success is within reach for every learner. The integration of machine learning algorithms into educational research has emerged as a transformative approach, offering insights that assist in optimizing learning outcomes, decision-making processes, and resource allocation. This paper introduces a new hybrid classification algorithm to predict student performance more accurately than existing methodologies.

Recent studies have demonstrated the efficacy of various machine-learning techniques in educational settings. From deep artificial neural networks identifying at-risk students to process mining enhancing MOOCs experiences, the landscape of educational data mining is rich and varied. However, each of these methods, while impactful in their own right, presents limitations when applied in isolation.

To enhance accuracy and introduce a unique approach compared to existing work, we have implemented a PHC that uses the optimal combination of RF, C4.5, and CART classifiers. This novel hybrid algorithm aims to combine the strengths of these individual classifiers to achieve superior predictive performance. Our motivation stems from the belief that a collective approach can address the shortcomings of singular algorithms, thereby providing a more holistic and accurate tool for educational practitioners. Hybrid classification models can be applied to many applications in other fields such as in education ^[1], agriculture ^[2], environment ^[3], materials ^[4], and optics ^[5].

The PHC has the potential to generate more accurate predictions and classifications related to students' performance, benefiting educational professionals, researchers, and policymakers in the education field. By leveraging the combined capabilities of RF, C4.5, and CART, the PHC is poised to offer significant advancements in predicting student outcomes. This paper details our hybrid classification algorithm's development, evaluation, and application, demonstrating its effectiveness through a dataset obtained from the UCI machine learning repository.

Our contribution to educational data mining with the PHC underscores the importance of innovative, data-driven approaches to understanding and enhancing student performance. As we navigate the complexities of educational needs and the vast potential of machine learning, the PHC represents a step forward in our collective effort to foster academic success and resilience among students globally.

The rest of this paper is structured as follows: Section 2 provides a literature review regarding the use of classification algorithms in education. Section 3 introduces the classification algorithms employed in this research, describes the data set used, presents an exploratory data analysis, details the experimental setup, evaluation measures utilized, and, finally, discusses the performance results of all algorithms. Section 4 concludes the key results and suggests possible future research directions.

2.   Related work

Institutions of higher learning worldwide are deeply invested in ensuring that their students achieve academic excellence. Pursuing academic achievement is a top priority for these institutions as it is a vital component in the development of well-rounded individuals who are prepared to make meaningful contributions to society. Machine learning algorithms can help institutions improve student learning outcomes, make better decisions, predict future trends and behavior, and optimize resource allocation. Therefore, we investigated the application of various machine-learning techniques in the field of education.

In recent years, the integration of machine learning algorithms in educational research has gained substantial attention, particularly in predicting student performance. Waheed et al. ^[6] used a deep artificial neural network to predict at-risk students based on unique handcrafted features extracted from click-stream data in virtual learning environments, providing early intervention measures. Their findings showed that the presented model outperforms other models, such as logistic regression and support vector machine algorithms. The study also found that students interested in reviewing past lectures' content performed better academically.

Umer et al. ^[7] developed a process mining technique to enable early predictions for enhancing students' learning experience in MOOCs. The study evaluates the effectiveness of various machine learning methods combined with process mining features. The research evaluates four machine learning classification techniques commonly used in the literature to predict overall performance outcome and observe weekly progression. The techniques include logistic regression, Naive Bayes, random forest, and K-nearest neighbors. Their results showed that the Naive Bayes method outperformed all other methods with an 89% accuracy rate. Another study was conducted to predict student performance by analyzing student-related data ^[8]. The data includes the scores of various assessments such as class tests, attendance, assignments, and midterms. The Levenberg Marquardt (MLA) deep learning and deep neural network algorithm were used in this study. The performance of the algorithms was assessed using different metrics such as recall, precision, accuracy, and F1 score. According to the findings, the MLA algorithm outperformed the other algorithms with an accuracy rate of 88.6% ^[8].

Morilla et al. ^[9] conducted a study aimed at predicting students' mathematics performance through the application of various machine learning algorithms, namely Naive Bayes, multiple linear regression, and decisions trees. Their analysis leveraged a dataset encompassing 144 students, capturing a range of academic metrics including attendance ratings, recitation scores, quiz results, midterm and final exam grades, alongside overall final grades. It was determined that the midterm exam rating stood out as the most significant predictor of students' overall performance. To assess the efficacy of their proposed classification algorithms, a 10-fold cross-validation method was utilized. The findings revealed that the Naive Bayes algorithm outperformed the others, achieving an accuracy rate of 73.61%, closely followed by the decision tree algorithm at 72.22%. On the other hand, the multiple linear regression algorithm lagged behind with an accuracy rate of 70.2%.

Mueen et al. ^[10] utilized three classification algorithms to predict and analyze the academic performance of students based on their academic records as well as their participation in forums. They used neural networks, decision trees, and the Naive Bayes algorithms based on the data collected from two undergraduate courses. Their findings indicated that the Naive Bayes algorithm achieved the highest prediction accuracy of 86% compared to the other two algorithms. Shahiri et al. ^[11] conducted a systematic literature review on predicting student performance. Their research paper aimed to provide an overview of data mining methods for predicting student performance. The paper delved further into the application of a prediction algorithm to identify the most important attributes in a student's data, enabling educators to tailor their teaching methods accordingly.

Previous studies indicate that we can use various classification algorithms to predict students' academic performance and address related educational issues. In this research paper, we propose a new hybrid classification algorithm that performs better than individual algorithms. It combines the strengths of various algorithms to provide superior accuracy and efficiency. This algorithm has been found to perform better than many other algorithms currently available in the literature when predicting student performance. We evaluated the performance of all algorithms in this paper using a combination of recall, precision, F1-score, and accuracy metrics.

3.   Materials and methods

3.1.   Classification algorithms

We have employed a diverse range of classification techniques to make more precise predictions about student achievement. These methods have enabled us to identify and analyze various factors that affect academic performance and ultimately generate more accurate predictions. These techniques encompass RF, C4.5, CART, SVM, NB, KNN, and our PHC.

3.1.1.   Random forest (RF)

Random forest is an ensemble learning method that operates by constructing many decision trees during training and outputting the mode of the classes (classification) or the individual trees' mean prediction (regression). Each tree is constructed using a random subset of the training data and a random subset of features, thereby reducing overfitting and improving robustness. Random forest has gained popularity due to its ability to effectively handle high-dimensional data and nonlinear relationships. For more details and information see ^[12].

3.1.2.   C4.5

C4.5 is a decision tree algorithm used for classification tasks. It builds decision trees based on the information gain criterion, which measures the effectiveness of splitting data at each node. C4.5 recursively splits the data into subsets based on the attribute that maximizes information gain until a stopping criterion is met, such as reaching a maximum tree depth or when all instances belong to the same class. C4.5 is known for its simplicity and interpretability. C4.5 employs a top-down, greedy approach to recursively split the data set based on the most informative attribute at each node. It handles both discrete and continuous attributes and can handle missing attribute values by estimating them based on available data. For further details and insights, refer to ^[13].

3.1.3.   Classification and regression trees (CART)

CART is another decision tree algorithm used for both classification and regression tasks. Like C4.5, CART builds binary trees by recursively partitioning the input space into regions that minimize impurity (for classification) or variance (for regression). CART differs from C4.5 in its splitting criterion and handling of categorical variables. CART is widely used due to its versatility and ability to handle various types of data. CART constructs binary trees by selecting the best split at each node to maximize purity (for classification) or minimize variance (for regression). It handles both categorical and continuous variables and can handle missing data. CART can be easily interpreted and visualized, making it useful for decision-making tasks. For additional information and clarification, see ^[14].

3.1.4.   Support vector machines (SVM)

SVM is a supervised learning algorithm used for classification and regression tasks. It operates by finding the optimal hyperplane that separates instances of different classes in the feature space while maximizing the margin, i.e., the distance between the hyperplane and the nearest data points (support vectors). SVM can handle linear and nonlinear relationships using kernel functions such as linear, polynomial, and radial basis function (RBF) kernels. SVM is effective in high-dimensional spaces and can separate classes in nonlinear feature spaces using kernel functions. SVM also has a regularizing parameter that helps control overfitting. For further insights and elaboration, refer to ^[15].

3.1.5.   Naive Bayes (NB)

Naive Bayes is a probabilistic classification algorithm based on Bayes' theorem with the assumption of independence between features. Despite its simplistic assumption, Naive Bayes often performs well in practice, especially for text classification tasks. It calculates the probability of each class given the input features and selects the class with the highest probability as the predicted class. Naive Bayes assumes that features are conditionally independent given the class, which simplifies the calculation of the posterior probability. It is computationally efficient and requires a small amount of training data. For further reading, refer to ^[16].

3.1.6.   K-nearest neighbors (KNN)

KNN is a non-parametric, instance-based learning algorithm used for classification and regression tasks. It operates by assigning a new data point to the majority class (for classification) or averaging the values of its nearest neighbors (for regression) in the feature space. KNN's simplicity and intuitive approach make it popular for various types of data and applications. KNN is a non-parametric algorithm that stores all available cases and classifies new cases based on a similarity measure (e.g., distance functions). It is simple and easy to implement, but it can be computationally expensive for large datasets since it requires calculating distances between all pairs of data points. For additional insights, see ^[17].

3.1.7.   Proposed hybrid classifier (PHC)

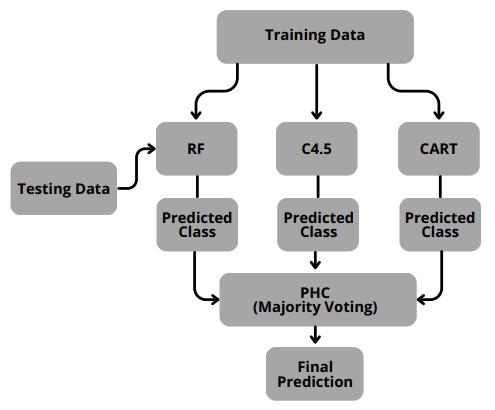
This research paper introduces a novel hybrid classification algorithm that combines multiple classification algorithms. Our proposed algorithm is based on an ensemble of the random forest, C4.5, and CART algorithms, designed to predict students' performance. The hybrid classifier first trains each algorithm with the given training set. Once the training process is complete, the hybrid classifier then proceeds to provide the testing set to each of the algorithms. Each algorithm predicts a class label for each instance in the testing set. In the final prediction stage, the hybrid classifier selects the majority voting class label. Integrating multiple classification algorithms aims to produce superior results compared to a single algorithm. Hybrid classifiers that use voting-based aggregation can improve the overall performance of the hybrid classifier by reducing individual classifier biases and errors. When individual algorithms are proficient in different aspects or capture different patterns in the data set, they become particularly useful. Figure 1 illustrates the concept of our proposed hybrid classifier.

3.2.   Data source

The data set used in this paper is obtained from the UCI repository of machine learning data sets ^[18]. It was collected from two Portuguese high schools through school reports and questionnaires. The data set concerns students' performance in mathematics. It consists of 395 students with diverse attributes such as grades, demographics, social factors, and school-related features. Cortez and Silva ^[19] illustrate the detailed description of this data set. According to them, the data set can be modeled under binary or multi-classification tasks. In this paper, we consider a binary classification task. The target variable, which originally had numerical values, was converted to a binary variable. According to ^[19], students pass if their final grade is equal to or greater than 10; otherwise, they fail. This data set does not contain missing values. Table 1 summarizes the characteristics of each attribute variable in the data set.

3.3.   Exploratory data analysis

In this section, we delve into the student performance dataset from the UCI machine learning repository and perform exploratory data analysis (EDA). This process will enable us to explore the dataset's various features, identify patterns, and gain insights into the data distribution, shape, and relationships between different variables. The EDA helps us to uncover valuable insights into attribute variables' prevalence and relationships. By the end of this analysis, we will have a more comprehensive understanding of the student performance data set and be better equipped to draw meaningful conclusions from it. The detailed presentation of the results of the EDA analyses can be found in this section. The experiments were conducted using the R statistical software.

Box plots in Figure 2 provide a quick visualization of the distribution of numerical attribute variables, revealing several key trends in student performance data:

● Most students are clustered around the median age, with some notable exceptions.

● The mother's education level is slightly skewed towards higher education.

● Commute and study times are consistent, with a few outliers suggesting longer travel times.

● Most students have not failed any classes, though a minority have failed once or three times, suggesting a need for targeted support.

● Family relations and social activities appear positively skewed, indicating good social support overall.

● Health issues and absences show greater variability, indicating a link to academic challenges.

● First and second period grades are symmetrically distributed, with a few students showing exceptional high or low performance.

● Outliers clearly affect the absence attribute variable. Hence, we use the Winsorization method ^[20], which replaces outliers with the observations closest to them. This is done to limit the effect of outliers on the performance of classifiers. For example, the identified outliers in the (absences) attribute variable have negatively affected the overall performance prediction of classification algorithms. However, using the Winsorization approach avoids this problem and enhances the overall accuracy.

Bar plots in Figure 3 provides a visual representation of the categorical attribute variables, where the horizontal coordinates represent the levels of each attribute variable and the vertical coordinates represent their frequencies. This visual representation assists us in identifying any imbalances or biases that may exist within the data set. For instance, we can see that the 'higher' attribute variable is imbalanced, where most instances concentrate on the 'Yes' option. It can also be seen that the father's job (Fjob) attribute variable has five levels, but most of the instances concentrate on the 'other' level. This information is crucial for understanding how attribute variables can affect predicting and classifying student performance.

Figure 4 illustrates a heatmap that visualises the correlation between variables, highlighting the eight attributes most strongly correlated with the class variable. Each heatmap cell quantifies the correlation between two attributes, where a value below zero indicates a negative correlation, above zero denotes a positive correlation, and exactly zero signifies no correlation. The standardized measure's correlation coefficient ranges from -1 (indicating a perfect negative correlation) to +1 (indicating a perfect positive correlation). Notably, the strongest correlation observed is between the grades from the first and second-periods, with a correlation coefficient of 0.85. Significant correlations are also observed between the first and second-period exam grades and the class variable. Such correlations are anticipated, given that student grades often interrelate. Morilla et al. corroborate this finding, noting the significant impact of midterm grades on overall student classification ^[9].

3.4.   Evaluation measures

In this paper, a 10-fold cross-validation scheme has been applied to evaluate the performance of all classifiers. The 10-fold cross-validation method divides the data set into ten equal parts. Then, the model is trained on nine of these parts and tested on the remaining part. This process is repeated ten times, so each part is utilized for testing once. The model's performance is estimated by averaging the results of 10 experiments, providing a more accurate outcome than a single experiment. In order to assess and compare the performance of all classifiers, four performance evaluation measures are used, which are recall, precision, F1-score, and accuracy. Before we introduce evaluation measures, we clarify some concepts using a sample confusion matrix, as shown in Table 2. Note that TN, TP, FN, and FP are abbreviations for true negatives, true positives, false negatives, and false positives, respectively. The description of evaluation measures is as follows.

The most commonly used measure to evaluate the effectiveness of classification algorithms is accuracy. Accuracy refers to the ratio of correctly classified samples to the total number of samples, and is given by

F-score is defined as the harmonic mean between precision and recall, and is given by

Recall is defined as the ratio of the total number of positive predicted instances to the total number of positive instances, and is given by

Precision is defined as the ratio of true positive predicted instances to the total number of positive instances, and is given by

These measures collectively provide a comprehensive evaluation of a classification model's performance and guide the necessary adjustments to optimize its effectiveness. All the evaluation measures have been computed for all classifiers using a 10-fold cross-validation scheme, where the average results have been reported.

3.5.   Results and discussion

This paper presents a Proposed Hybrid Classifier (PHC) that comprises three classification algorithms, random forest (RF), C4.5, and CART, to predict student performance. The study compares the performance of our hybrid classifier with six commonly used algorithms, including RF, C4.5, CART, SVM, NB, and KNN. Each classifier is evaluated using various metrics such as recall, precision, F1 score, and accuracy. This analysis aims to assess existing algorithms and position our PHC in relation to them. By evaluating each algorithm's performance measures, we can better understand the improvements and limitations concerning student performance prediction using classification algorithms. Furthermore, the PHC can be effectively utilized for various deep learning and machine learning applications besides education. Hybrid models have been shown to improve accuracy by 30% compared to any single model ^[21].

The results for all classifiers are presented in Table 3. The results demonstrate a notable superiority in the performance of the PHC algorithm over other classification algorithms in terms of precision, F1 score, and accuracy measures. However, the PHC and C4.5 algorithms perform similarly with respect to recall metric and outperforms all other algorithms with slightly better performance by the C4.5 algorithm. Recall, also known as sensitivity, assesses the model's ability to identify all positive instances correctly. Across all algorithms, the C4.5 and PHC algorithms are the optimal options with this measure.

For the accuracy measure, our PHC outperforms all other classifiers with an accuracy rate of 92.40%. The RF, C4.5, and CART classifiers perform better than other classifiers, whereas the SVM and NB have the worst performance with this measure. Again, for precision and F1 score measures, the PHC performs better than all algorithms, while the RF, C4.5, and CART algorithms outperform the SVM, NB, and KNN algorithms. Among single classifiers, the NB classifier was found to have the lowest recall metric, with scores of 79.72%. The SVM classifier was found to have lower precision and F1-score than all other classifiers. Specifically, the precision was 71.57% and the F1-score was 77.18%. These performance metrics indicate that the SVM classifier may not be the optimal choice for a given task based on these metrics. This might be due to the nature of the SVM algorithm, which may not effectively handle the specific complexities and characteristics of the educational data set used in this paper.

Table 4 shows time complexities for all classifiers. The KNN classifier achieves the shortest execution time with nearly the same time as the NB classifier. The C4.5, CART, and SVM classifiers came after that with similar execution times. Finally, the RF and PHC classifiers took the longest execution time compared to other classifiers. This is because they utilize ensemble methods to calculate the accuracy and, hence, more time to achieve better results than other single classifiers.

The findings of this research have significant implications for the education industry. Classification algorithms like PHC can help predict student performance and implement support strategies. This classifier's predictive ability can help identify students at risk of underperformance. Then, educators can efficiently allocate resources where students are most needed. Incorporating this paper's findings into educational management systems can enable real-time monitoring of student progress. Educational institutions could use PHC to identify potential declines in student performance before they lead to failure. This would allow for timely support to help students overcome academic challenges.

According to the experimental results, the PHC, which is based on various classifiers, is a highly effective tool for predicting students' academic performance. The results of our research indicate that the PHC can provide reliable and accurate predictions in a range of educational settings. We therefore recommend its use as a valuable resource for educators and administrators seeking to maximize student success. The PHC combines the strengths of individual classification algorithms to deliver a final prediction that benefits from their collective knowledge. The PHC is particularly effective when no classification algorithm can provide a sufficiently accurate prediction. This approach has been shown to improve the accuracy of classification tasks in education. In summary, it has been proven that the PHC performs competitively compared to six individual algorithms. Thus, it is suggested that the PHC be effectively utilized to evaluate students' academic performance.

Figure 5 illustrates the significance of various features in predicting student performance using a permutation-based importance measure derived from a random forest model. This technique assesses the impact of each feature by evaluating the deterioration in the model's accuracy when the values of that feature are randomly shuffled. Consistent with expectations, previous grades G2 and G1 emerge as the top influencers, strongly affecting the model's predictions. Notably, the number of times students go out with friends (goout) and their age (age) also appear to be influential, suggesting that social habits and maturity may have roles in academic performance. The reasons for choosing a school (reason), job of the father (Fjob), and family size (famsize) complete the list of top features, indicating that both school-related choices and family background factors contribute to the variability in student grades.

The combination of decision trees (C4.5 and CART) in the PHC classifier leverages the strengths of each algorithm to capture diverse data patterns more effectively. The superior performance of the PHC classifier can be attributed to its ensemble approach, which balances bias and variance, reducing the risk of overfitting seen in individual classifiers like SVM and NB. The interpretability of decision tree-based methods (RF, C4.5, CART) aids in understanding feature importance, which aligns with the observed performance trends. As shown in Figure 5, the features 'G2' and 'G1' grades are the most critical predictors of student performance, followed by factors such as'goout', 'age', 'reason', 'Fjob', and 'famsize'. These features significantly impact predictions and are well-handled by these algorithms, demonstrating their capability to effectively capture and utilize the most relevant data attributes.

One limitation of this study is the reliance on data from the UCI machine learning repository, which may not fully represent the diverse educational environments worldwide. Additionally, the model complexity introduced by combining multiple algorithms could pose challenges in terms of computational resources and implementation scalability. Future research could explore the application of the PHC classifier to larger, more diverse datasets to enhance its generalizability. Investigating the integration of other machine learning techniques, such as deep learning models, into the hybrid approach may also offer further improvements in predictive performance.

4.   Concluding remarks

Predicting student performance can help educators and learners improve their teaching and learning processes. This study describes a unique hybrid classification technique that combines the strengths of random forest (RF), C4.5, and CART classifiers. This proposed hybrid classifier (PHC) was thoroughly tested against six traditional classification algorithms using recall, precision, F1-score, and accuracy metrics. Our findings show that the PHC algorithm outperforms single classification algorithms in terms of prediction performance. This improvement demonstrates effectiveness of combining multiple algorithms to address the diverse nature of educational data.

The practical applications of the PHC classifier in educational contexts represent a potential area for future study and development. The PHC's capacity to reliably predict student performance can help educational institutions identify individuals who may need further support, allowing for targeted interventions that are more likely to enhance student results. It also opens the door to personalized learning experiences in which educational content and teaching approaches may be tailored to each student's specific requirements based on predicted insights.

Based on the study findings, it is recommended that educators and policymakers consider adopting hybrid classification models like the PHC classifier to enhance predictive analytics in education. Such models can help identify students at risk of underperformance early, enabling timely and targeted interventions. Policymakers should also invest in the necessary infrastructure and training for educators to effectively implement and utilize these advanced analytical tools. By integrating data-driven insights into educational strategies, institutions can better support student success and optimize resource allocation.

Author contributions

Abdulmajeed Atiah Alharbi and Jeza Allohibi: Conceptualization, Formal Analysis, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence tools in the creation of this article.

Conflict of interest

The authors declare that they have no conflicts of interest.