Modified mildly inertial subgradient extragradient method for solving pseudomonotone equilibrium problems and nonexpansive fixed point problems

1.   Introduction

In ^[22], Muu and Oetti considered the equilibrium problem (EP) as a generalization of several problems in nonlinear analysis, and these problems include convex minimization, variational inequalities, Nash-equilibrium problems, fixed point problems, and saddle point problems ^[8,22]. The EP has applications in many mathematical models from various fields of applied science and engineering such as economics, physics, image restoration, finance, ecology, network elasticity, transportation, and optimization. Let $C$ be a nonempty, convex, and closed subset of a real Hilbert space $H$ and $g:C\times C\to \mathbb{R}$ be a bifunction such that $g(x, x) = 0$ for all $x\in C$. The EP, as defined by Muu and Oetti ^[22], is formulated as follows: Find $x^*\in C$ such that

The solution of the EP (1.1) is denoted by $EP(g)$. Due to the fact that many real-life problems are modeled with a pseudomonotone bifunction, several authors have considered solving EP (1.1) with pseudomonotone bifunction $g$; see, for example, ^[15,16,17] and the references therein. On the other hand, the theory of fixed points is an important concept in nonlinear analysis. Many problems in applied sciences and engineering can be formulated as fixed point problems. A point $x\in C$ is called a fixed point of a self mapping $T:C\to C$ if $Tx = x$. In this article, the set of all fixed point of $T$ is denoted by $F(T) = \{x\in C:Tx = x\}$. Finding the common solutions of EP and fixed points problems (FPP) is important because some mathematical models constraints can be expressed as EP and FFP. Some of these models can be found in several practical problems such as network resource allocation, signal processing, image restoration and so on ^[17].

In ^[32], Tada and Takahashi introduced the following hybrid method for approximating the common solution of monotone EP and FFP of nonexpansive mappings in real Hilbert spaces:

It is worthy to note that the method (1.2) requires solving a strongly monotonic generalized EP for point $z_m$: Find $z_m\in C$ such that

It is difficult to approximate the solutions of EP (1.1) when the bifunction assumption is weakened from monotone to pseudomonotone ^[17]. In 2008, Quoc et al. ^[28] considered a new method known as the extrgradient method (EM). Their results are extension and generalization of the results of Korpelevic ^[18] and Antipin ^[2] to the case of EP involving a pseudomonotone bifunction. In 2013, Ahn ^[1] considered an iterative method for finding the common solution of EP with a pseudomonotone bifunction and FPP of nonexpansive mappings. The major drawback of the methods in ^[28] and ^[1] is that, one needs to solve two strongly convex optimization problems in the feasible set $C$ in each iteration of the algorithms. In order to improve the extragradient method, Hieu ^[15] followed the results of Censor et al. ^[9,10] to introduce a Halpern-type subgradient extragradient method. This method involves a half-space in the second minimization problem. It is noticed that the Halpern-type method is dependent on Lipschitz-type constants of the bifunction and that these constants are difficult to determine. Recently, Yang and Liu ^[33] introduced a modified Halpern-type method which does not require the prior knowledge of the Lipschitz-type constants. Their method has a non-increasing step-size. In real Hilbert spaces, the authors proved a strong convergence theorem for approximating the common solution of pseudomonotone EP and FFP of nonexpansive mappings.

In order to speed up the process of solving the smooth convex minimization problem, Polyak originally presented and examined the idea of inertial extrapolation in ^[27] in 1964. Since then, scientists have employed this method to accelerate the rate at which many iterative processes converge. Since its conception, the inertial extrapolation approach has been refined, extended, and generalized by numerous authors; see ^[3,4,5,6,7] and the references therein. Relaxation techniques have proven to be an effective method for improving the rate of convergence in this field of study; see ^[23,24,25]. It is common knowledge that when inertial and relaxation techniques are combined, the results increase and the rate of convergence is higher than when either approach is used alone; see ^[19,20,26]. Very recently, Ceng et al. ^[11] introduced and studied a mildly inertial algorithm with a linesearch process for finding a common solution of the variational inequality problem and the common fixed-point problem of an asymptotically nonexpansive mapping and finitely many nonexpansive mappings by using a subgradient approach. For more details on the mildly inertial concept; see, ^[11,31] and the reference in them.

Is it feasible to introduce a new step-size rule in conjunction with a new double inertial extrapolation to solve a pseudomonotone inequality problem and a fixed point problem in the framework of Hilbert space?

Motivated by the above results, in this article, we propose a new self-adaptive inertial subgradient extragradient method which does not rely on the prior knowledge of the Lipschitz-type constants of the bifunction. The suggested method is used to approximate the common solution of pseudomonotone EP and FFP of nonexpansive in a real Hilbert space. Our method includes two modified mildly inertial terms which improve the speed of convergence of the suggested method. Under some mild conditions on the control parameters, we prove the weak convergence of the result of the suggested method. Furthermore, we present some numerical examples to demonstrate the computational advantage of our method over some well known method in the literature.

The remaining part of this article is arranged as follows: In Section 2, we give some useful results and definitions in this study. In Section 3, we present the suggested method and the necessary conditions for obtaining our main result. In Section 4, we establish the strong convergence results of the suggested method. In Section 5, we present a numerical experiment to show the efficiency of our method, and in Section 6, we give th conclusion of our study.

2.   Preliminaries

In this section, we begin by recalling some known and useful results which are needed in the sequel. Let $H$ be a real Hilbert space. We denotes strong and weak convergence by "$\rightarrow$" and "$\rightharpoonup$", respectively. For any $x, y \in H$ and $\alpha \in [0, 1],$ it is well-known that

Definition 2.1. ^[8,12,14] Let $g: C\times C \to \mathbb{R}$ be a mapping. Then $g$ is said to be

(a) Strongly monotone on $C$ if there exists a constant $\tau > 0$ such that

for all $x, y\in C;$

(b) Monotone on $C$ if

for all $x, y\in C;$

(c) Strongly pseudomonotone on $C$ if there exists a constant $\gamma > 0$ such that

(d) Pseudomonotone on $C$ if

(e) Satisfying a Lipschitz-like condition if there exist two positive constants $L_1, L_2$ such that

Let $C$ be a nonempty, closed and convex subset of $H.$ For any $u\in H,$ there exists a unique point $P_{C}u\in C$ such that

The operator $P_C$ is called the metric projection of $H$ onto $C.$ It is well-known that $P_C$ is a nonexpansive mapping and that $P_C$ satisfies

for all $x, y \in H.$ Furthermore, $P_C$ is characterized by the following property:

and

for all $x\in H$ and $y\in C.$ A subset $C$ of $H$ is called proximal if for each $x\in H,$ there exists $y\in C$ such that

The Hausdorff metric on $H$ is as follows:

for all subsets $A$ and $B$ of $H.$

The normal cone $N_C$ to $C$ at a point $x\in C$ is defined by $N_C(x) = \{z\in H:\langle z, x-y\rangle \geq 0, \; \forall y\in C\}.$

Lemma 2.1. ^[13] Let $\{\delta_n\}$ and $\{\omega_n\}$ be sequences of positive real numbers, such that

Then the following holds

where $M = \max\{\delta_1, \delta_2\}.$ Moreover, if $\sum_{n = 1}^{\infty}\omega_n < \infty,$ then $\{\delta_{n}\}$ is bounded.

Lemma 2.2. ^[21] Let $\{x_m\}$ be a sequence in $H$ such that the following conditions hold:

(1) $\lim_{m\to \infty}\|x_m -x\|$ exist for any $x\in H;$

(2) all weak cluster points of $\{x_n\}$ lies in $H$.

Then $\{x_m\}$ converges weakly to some point in $H.$

Lemma 2.3. ^[30] Let $\{\delta_m\}, \{\beta_m\}$ and $\{\omega_m\}$ be sequences of positive real numbers, such that

If $\sum_{m = 1}^{\infty}\omega_m < \infty,$ and $\sum_{m = 1}^{\infty}\beta_m < \infty.$ Then the limit of $\delta_m$ exists.

Lemma 2.4. ^[12] Let $C$ be a convex subset of a real Hilbert space $H$ and $\phi:C \to \mathbb{R}$ be a subdifferential function on $C.$ Then $x^*$ is a solution to the convex problem: $\mathit{\text{minimize}}\{\phi(x): x\in C\}$ if and only if $0\in \partial\phi(x^*) + N_C(x^*),$ where $\partial\phi(x^*)$ denotes the subdifferential of $\phi$ and $N_C(x^*)$ is the normal cone of $C$ at $x^*.$

3.   Proposed algorithm

Assumption 3.1. Condition A. Suppose that $C$ is a nonempty, closed convex subset of a real Hilbert space $H.$ Let $g:C\times C\to \mathbb{R}$ satisfies the following conditions:

(1) $g$ is pseudomonotone on $C,$ $g(x, x) = 0$ for all $x\in H$ and satisfies the Lipschitz-type condition (2.8) on $H$ with positive constants $c_1, c_2;$

(2) $g(\cdot, x)$ is sequentially weakly upper semi-continuous on $C$ for each fixed $x\in C;$

(3) $g(x, \cdot)$ is convex, lower semi-continuous and subdifferential on $C$ for every fixed $x\in C;$

(4) $\{T_m\}$ is a sequence of nonexpansive mapping;

(5) $S:C\to C$ is a nonexpansive mapping;

(6) The solution set $\Omega = Ep(g)\cap F(S)\neq \emptyset.$

Next, we present the proposed modified mildly inertial subgradient extragradient algorithm (Algorithm 3.1) and prove its weak convergence results.

Remark 3.1. The above iterative method is quite different from the usual double iterative methods in the literature. The role of $T_m$ is justified in our numerical experiment.

4.   Convergence analysis

Lemma 4.1. The sequence $\tau_{m+1}$ generated by Algorithm 3.1. Then,

Proof. Using (3.1) in Algorithm 3.1 and (2.8), we have

Thus, the sequence $\tau_{m}$ is nonincreasing and has a lower bound of $\frac{\mu}{4\max\{c_1, c_2\}}.$ It then follows that, there exists

□

Theorem 4.1. Let $\{x_m\}$ be the sequence generated by Algorithm 3.1 such that the Assumption 3.1 holds. Then, $\{x_m\}$ converges weakly to a point $p\in \Omega.$

Proof. Let $p\in \Omega.$ Using Algorithm 3.1, Lemma 2.4 and the definition of $u_{m},$ we have

Let $v_m \in \partial_2g(y_m, u_{m})$ and $\chi\in N_{C_m}(u_{m})$ such that

since $\chi \in N_{C_m}(u_{m}),$ then

and since $p\in Ep(g),$ we have

In addition, since $v_m\in \partial_2g(y_m, u_{m}),$ we obtain

Combining (4.5) and (4.6), we have

Since, $p\in \Omega,$ then $g(p, y_m)\geq 0,$ thus, using the fact that $g$ is pseudomonotone, we have $g(y_m, p)\leq 0.$ Hence, we get

Using the fact that $u_{m}\in C_{m},$ we obtain

so,

Since $\psi_m\in \partial_2g(z_m, y_m),$ and the definition of subdifferential, we obtain

it then follows that

Using (4.8) and (4.9), we have

which implies that

Thus, using (3.1), we have

Clearly, $\lim_{m\to \infty}\frac{\mu\tau_{m}}{2\lambda\tau_{m+1}} = \frac{\mu}{2\lambda} < 1.$ Thus, we have

In addition, using Algorithm 3.1, we have

Using Algorithm 3.1, (4.13), and the definition of $S,$ we have

From (4.14) and (4.15), we have

where $\omega_m = \gamma_m+\theta_m+\theta_m\gamma_m.$ Using Lemma 2.1, we have that $\{x_m\}$ is bounded, consequently the sequences $\{w_m\}, \{z_m\}$ and $\{u_m\}$ are bounded. It then follows that $\sum_{m = 1}^{\infty}\omega_m\|x_{m-1}-p\| < \infty.$ Using (4.16) and Lemma 2.3, we have that $\lim_{m\to\infty}\|x_m-p\|$ exists. As such from (4.16), we obtain that

Thus, we obtain

From (4.14), we have that

Thus, using (4.15) and (4.19), we have

which implies that

Using (4.18), we have

which implies that

Furthermore, from Algorithm 3.1, we have

Using (4.18), we have

Using (4.22) and (4.24), we have

We need to establish that the sequence $\{x_m\}$ converges weakly to $x^*\in \Omega.$ Since $\{x_m\}$ is bounded, there exists a weakly convergent subsequence of $\{x_m\}.$ Suppose that $\{x_{m_{k}}\}$ is the subsequence of $\{x_m\}$ such that $\{x_{m_{k}}\}$ converges weakly to $x^*.$ Furthermore, using (4.25), we obtain that a subsequence of $\{u_n\}$ say $\{u_{n_k}\}$ converges weakly to $x^*,$ and using (4.22) and by the demiclosedness, we have that $x^*\in F(S).$ Using (4.9) and the subdifferential of $g,$ we have

taking limit as $k\to \infty$ and using Assumption 3.1(1) and (3), and the fact that $\lim_{k\to \infty}\tau_{m_k} = \tau > 0,$ we have that $g(x^*, x)\geq 0$ for all $x\in C.$ Hence, $x^*\in \Omega.$ Using Lemma 2.2, we obtain that $\{x_m\}$ converges weakly to $p$ and $p\in \Omega.$ □

5.   Numerical example

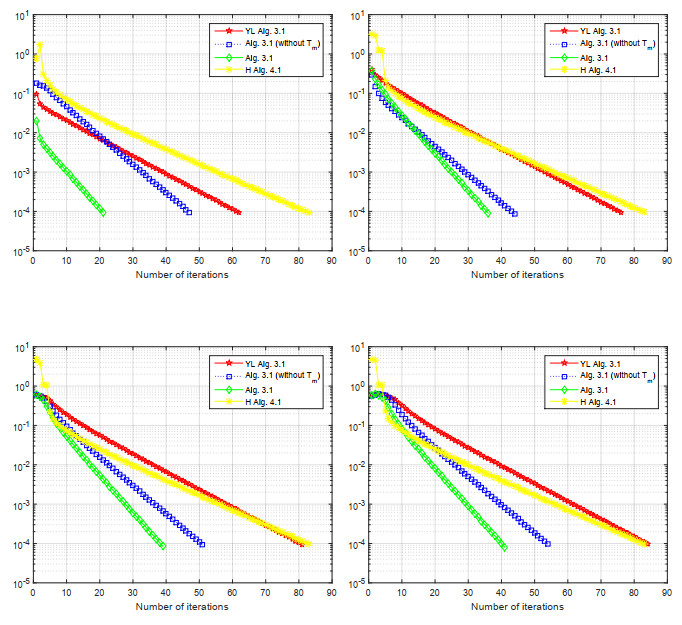
In this section, some numerical examples are given to authenticate our main result. We compare the performance of the numerical behavior of our Algorithm 3.1 (shortly, Alg. 3.1) with Algorithm 3.1 in ^[33] (shortly, LY Alg. 3.1) and Algorithm 4.1 in ^[15] (shortly, H Alg. 4.1). We perform all numerical simulations using MATLAB R2020b and carried out on PC Desktop Intel^® Core^TM i7-3540M CPU @ 3.00GHz $\times$ 4 memory 400.00GB.

Example 5.1. Let $H = \ell_2(\mathbb{R}) = \{x = (x_1, x_2, ..., x_k, ...), , x_k\in \mathbb{R}\, \text{and}\, \sum_{k = 1}^{\infty}|x_k|^2 < \infty\}$ with inner product $\langle\cdot, \cdot\rangle:\ell_2\times \ell_2\to \mathbb{R}$ and norm $\|\cdot\|:\ell_2\to \mathbb{R}$ defined by $\langle x, y\rangle = \sum_{k = 1}^{\infty}x_ky_k$ and $\|x\| = (\sum_{k = 1}^{\infty}|x_k|^2)^\frac{1}{2}$, where $x = \{x_k\}^\infty_{k = 1}$, $y = \{y_k\}^\infty_{k = 1}$. Now, let $C = \{x\in H:\|x\|\leq1 \}$. The bifunction $g:C\to C$ is defined by $g(x, y) = (3-\|x\|)\langle x, y-x\rangle, \forall x, y\in C$. As in ^[29], one can easily verify that $g$ is a pseudomonotone which is not monotone and $g$ fulfills the Lipschitz-type condition with constants $c_1 = c_2 = \frac{5}{2}$. Let $T_m:\ell_2\to \ell_2$ be defined by $T_m = \frac{x}{5m}$, for all $m\in \mathbb{N}$, $x\in C$ and define $S:\ell_2\to \ell_2$ by $Sx = \frac{x}{4}$, where $x = (x_1, x_2, ..., x_k, ...)$, $x_k\in \mathbb{R}$. Now, we consider the following parameters for the various methods:

$\bullet$ For Alg. 3.1: $\lambda = 2.4$, $\mu = 0.7$, $\gamma_m = \theta_m = \frac{1}{10m^2+1}$, $\beta_m = \frac{1}{5m}$,

$\bullet$ For LY Alg. 3.1: $\alpha_m = \frac{1}{1000(m+2)}$, $\beta_m = 0.8$, $\lambda_0 = \frac{1}{4}$, $\mu = 0.7$.

$\bullet$ For H Alg. 4.1: $\lambda = 2.4$, $\alpha_m = \frac{1}{1000(m+2)}$ and $\beta_m = 0.8$.

Next, we consider the following initial values:

Case A: $x_0 = (0, 1, 0, ..., 0, ...)$, $x_1 = (1, 1, 1, ,..., 0, ...)$,

Case B: $x_0 = (1, 1, 0, ..., 0, ...)$, $x_1 = (0, 1, 1, ,..., 0, ...)$,

Case C: $x_0 = (1, 0, 1, ..., 0, ...)$, $x_1 = (1, 0, 1, ,..., 0, ...)$,

Case D: $x_0 = (1, 0, ..., 0, ...)$, $x_1 = (1, 1, 0, ,..., 0, ...)$.

For the numerical computation, we used the stopping criterion $TOL_n = \|x_{m+1}-x_{m}\| < 10^{-4}$ and we obtained the following Table 1 and Figure 1:

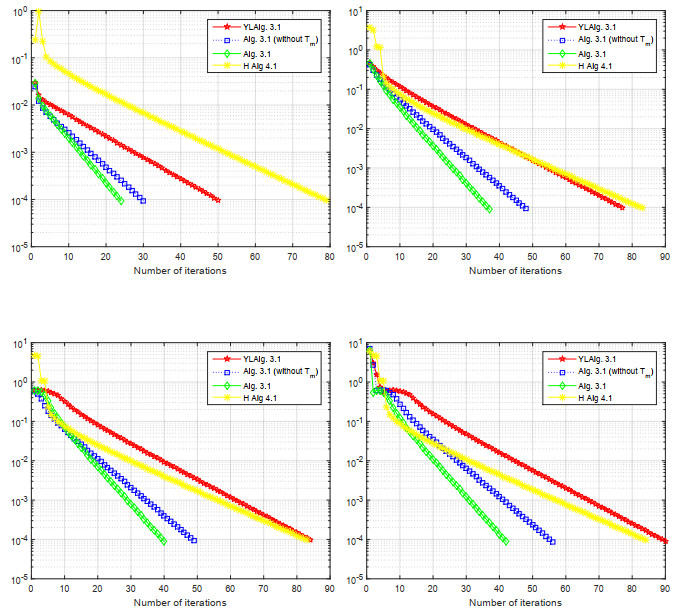
Example 5.2. Let $H = L_2([0, 1])$ with the inner product $\langle x, y\rangle = \int_{0}^{1}x(t)y(t)dt$ with inner product $\|x\| = (\int_{0}^{1}x^2(t)dt)^{\frac{1}{2}}$ for all $x, y\in L_2([0, 1])$. We define the set $C$ by $C = \{x\in H:\int_{0}^{1}(s^2+1)x(s)ds\leq 1\}$ and the function $g:C\times C\to \mathbb{R}$ is defined by $g(x, y) = \langle Bx, y-x\rangle$, where $Bx(s) = \max \{0, x(s)\}$, $s\in [0, 1]$ for all $x\in H$. Now, let the mapping $T_m:C\to C$ be defined by $T_mx = \frac{x}{2m}$, for each $m\in \mathbb{N}$ and define $S:C\to C$ by $Sx = \frac{x}{3}$, for each $x\in C$. Now, we consider the following initial values:

Case I: $x_0 = s^3+1$, $x_1 = \sin (3s)$,

Case II: $x_0 = \frac{\sin(4s)}{30}$, $x_1 = \frac{\cos (3s)}{3}$,

Case III: $x_0 = \frac{\exp (3s)}{80}$, $x_1 = \frac{\exp (4s)}{80}$,

Case IV: $x_0 = s^3+s^2$, $x_1 = s^2+1$.

For the numerical computation, we use the same parameters as in Example 1. We consider the stopping criterion $Tol_m = \|x_{m+1}-x_{m}\| < 10^{-5}$ and the following Table 2 and Figure 2 are obtained.

Remark 5.1. From the Tables 1 and 2 and Figures 1 and 2, it is evident that our new method outperforms the compared methods.

6.   Conclusions

In this work, we have introduced a modified subgradient extragradient iterative algorithm for approximating the common solution of EP with pseudomonotone bifunction and FPP of nonexpansive mappings in a real Hilbert space. The proposed method employs a self-adaptive step-size and does not rely on the prior knowledge of the Lipscihtz-type constants of the pseudomonotone bifunctions. Under some mild conditions, we proved the weak convergence result of the new method. We have shown that the suggested method which includes two modified mildly inertial steps outperforms several well known methods in the existing literature.

Authors contributions

Francis Akutsah: Conceptualization, Writing-original draft; Akindele Adebayo Mebawondu: Conceptualization, Software, Writing-original draft; Austine Efut Ofem: Methodology, Software, Writing-original draft; Reny George: Validation, Funding acquisition, Formal analysis; Hossam A. Nabwey: Validation, Formal analysis; Ojen Kumar Narain: Supervision. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this work through the project number (PSAU/2024/01/78917).

Conflict of interest

The authors declare no conflict of interests.