Solitary waves of the generalized Zakharov equations via integration algorithms

1.   Introduction

With the advancement of computer methods, the study of the traveling wave solutions of nonlinear partial differential equations (NLPDEs) has become a key research area in various fields, including mathematics, physics, fluid dynamics, biology, engineering, and computer science. Over the past few years, considerable progress has been made in the area of establishing different approaches to obtaining exact solutions to NLPDEs, and this has greatly improved our understanding of nonlinear phenomena. Such nonlinear phenomena can be observed in many scientific and technological applications, such as plasma physics, nonlinear fiber optics, and the propagation of shallow water waves ^[1,2]. Scientists and engineers have successfully described many physical phenomena in recent decades by using macroscopic models in the form of NLPDEs, which can be solved for desired quantities ^[3,4,5]. The most popular examples of such models include the Schrödinger equation, which describes the properties of time-varying quantum states in quantum mechanics. In fluid mechanics, the Navier-Stokes equation is widely used to describe the main properties of incompressible fluids such as velocity, density, temperature, pressure, and viscosity. Furthermore, in the presence of viscosity, the Zakharov equations are considered as continuum models that describe the behavior of blood plasma in biological fluids ^[6]. However, there is still much to discover by exploring a series of new exact optical solutions to such models with the aim of providing further explanation of physical phenomena of practical interest, from which the NLPDE is formed, and to apply them in practical life. In addition, the stability analysis can be successfully performed if the solutions of NLPDEs are available in closed form.

Solitary and soliton waves are special classes of traveling wave solutions with special properties ^[7]. These special properties are of fundamental importance in efforts to determine the behavior of the solution, which we seek to understand. Solitary waves arise naturally in many engineering and scientific applications, such as the intensity of light and the elevation of surface water in optical fibers. On the other hand, a soliton is considered to be a nonlinear solitary wave which can provide important insight into the particular features of solitary waves and form a special class of solutions to the generalized Zakharov equations (GZEs). Here, we focus on exploring new solitary solutions for a set of coupled equations, with the aim of deriving an adequate mathematical description for the system of interest.

Despite the great success of NLPDEs as a tool to describe nonlinear phenomena, not all of the complex systems are solvable. Even in some cases, if complex systems are solvable, the obtained solutions are not general; hence, they do not cover every possibility. Therefore, from a modern perspective, familiarity with all traditional and recently created techniques that have been designed to tackle these nonlinear systems is becoming increasingly important. Over the past few years, several techniques have been developed by scientists and mathematicians, such as the exact soliton solution ^[8,9,10], the $\tanh$-function technique ^[11], the method of sine-cosine ^[12], the auxiliary equation method ^[13], the F-expansion method ^[14], the exp-function technique ^[15,16], the variational iteration method ^[17], and the generalized Kudryashov approach ^[18]. A more detailed discussion on some recent work on the solutions of nonlinear wave theory can be found in various research papers (see, for example, ^{[19,20,21,22,23,24,25,26,27]}).

In 1972, Zakharov established a set of nonlinear evolution equations to model and investigate the electromagnetic properties of plasmas, which became known as the Zakharov equations ^[28]. These equations are also extensively used as fundamental models that govern the nonlinear dynamical systems, and to describe the evolution of Langmuir turbulence in the presence of strong turbulence effects; see, for example, the review by Goldman ^[29]. By implementing the extended hyperbolic functions approach, Shang et al. ^[30] explored multiple explicit traveling solutions to the Zakharov equations. Several analytical methods have been previously introduced that aim to explore the exact and explicit solutions to the Zakharov equation ^{[31,32,33,34,35,36]}.

In this paper, the GZEs which have been extensively used to model the propagation of Langmuir waves in plasmas are explored to find new solitary solutions by using four different algorithms. For the purpose of discussion, we introduce an example model in the class of nonlinear wave equations with constant coefficients

where $\beta, \; \beta_1, \; \gamma_1,$ and $\gamma_1$ are non-zero constants; and $\beta_2, \; \alpha_1,$ and $\alpha_2$ are real constants. By selecting appropriate values for these constants, we can obtain various equations, such as the nonlinear Schrödinger equations and the Davey-Stewartson equations which have been used to investigate the short-and long-wave resonances and other propagating-wave patterns ^[37]. By considering $v(x, t)$ to be the plasma density in one-dimensional systems and setting the above constants as follows: $\beta = 1$, $\beta_1 = -2\lambda$, $\alpha_1, \alpha_2 = -1$, $\gamma_1 = 2,$ and $\gamma_2 = -1$, the system of Eq (1.1) can be reduced to the GZEs as follows ^[38]:

where $\psi$ is the high-frequency electric field envelope and $v$ is the plasma density estimated from its equilibrium value. The coefficient $\lambda$ is a real constant that can be either positive or negative. Note that by setting $\lambda = 0$, the system (1.2) reduces to the classical Zakharov equations, which describe the nonlinear dynamical systems in plasma physics ^[39].

In recent years, an explosive growth of activities involving the use of several direct methods to find exact solutions for the GZEs due to their extensive applications in different fields has been seen, especially in the fields of fluid dynamics and plasma physics. For example, Borhanifar et al. ^[40] used the exp-function approach to construct periodic solutions and a generalized solitary of the GZEs. Wang and Li used an extended F-expansion method to obtain a number of periodic wave solutions to the GZEs ^[41]. The homotopy analysis method has been applied successfully by Abbasbandy et al. to the GZEs to obtain approximations of the analytic solutions ^[42]. He's variational technique ^[43,44] has been applied by Khan et al. to find soliton solutions of the GZEs ^[45]. By using the $q$-homotopy analysis transform method, Veeresha and Prakasha obtained the solution for fractional generalized Zakharov equations ^[46]. Here, we focus on applying four interesting integration methods to obtain new traveling wave solutions of GZEs. The obtained solutions exhibit various wave features including bright solutions and singular wave solutions. By using appropriate parameter values, the obtained solutions were plotted to visualize the dynamical behavior of the corresponding wave solutions. These new solutions show that these methods are simple, effective, and applicable mathematical tools to study the physical nature in different scientific fields, such as, physics, geophysics, engineering, optics, and computer science.

Among the recent techniques used to find the exact traveling wave solutions to NLPDEs is the $(G'/G)$-expansion approach which has been proposed by Wang et al.^[47]. This approach is used widely as a direct and concise technique, where $G(\xi)$ is a function that satisfies the NLPDE of second order:

where $\lambda$ and $\mu$ are arbitrary constants. As a generalization of the $(G'/G)$-expansion method, Li et al. ^[48] proposed the modified $(w/g)$-expansion method to construct some new traveling waves for the Vakhnenko equation, which is a very important nonlinear evolution equation that can be used to describe high-frequency wave propagation through relaxing media. Following this method, we aim to illustrate and explore the effectiveness, reliability, and possibility of expanding the applications of four different algorithms by using the GZEs. Also, considering the GZEs as a realistic plasma model motivated us to investigate the solitary wave solutions of such a system ^[49].

In this paper, Section 2 briefly reviews the methodology of the modified ($w/g$)-expansion method. Section 3 begins with a brief description of the extended rational ($w/g$)-expansion method and its application. The first three used approaches, namely, the modified $(g'/g^2)$-expansion method, $(g')$-expansion method, and the generalized simple $(w/g)$-expansion method are considered and new solitary wave solutions for the resulting equations are obtained. The addendum to Kudryashov's method (AKM), which has been recently introduced by Zayed et al. ^[50], is the fourth method used in this paper (Section 4); here, it is applied to the GZEs with the aim of demonstrating the efficiency of this method as a tool to obtain a solitary wave solution for a system of nonlinear evolution equations. With the assistance of symbolic computation software, we present Section 5 with graphical descriptions of the results obtained in this study. Although we focus on investigating the GZEs, we expect that the presented direct approaches should also be able to describe the physical phenomena of a variety of nonlinear problems in different fields.

2.   Summary of the modified ($w/g$)-expansion approach

This section briefly describes the procedure of the modified ($w/g$)-expansion method for determination of solitary wave solutions of nonlinear equations as discussed in ^[48,51]. Consider the following NLPDE with two independent variables $x$ and $t$:

where $u(x, t)$ is the solution of the above equation and the subscripts represent the partial derivatives of $P$, which is a nonlinear function of its arguments in general. The above NLPDE can be solved via the following steps:

Step 1. To convert the spatial and temporal variables $x$ and $t$, respectively, into a compound variable $\xi$, we seek the traveling wave transformation in the following form:

where $U = U(\xi)$ is an unknown function and the constant $k$ is the wave speed. This transformation given by Eq (2.2) allows us to transform the NLPDE (2.1) to the following ordinary differential equation (ODE):

where $Q$, in general, is a polynomial function in $U(\xi)$ and its derivatives $U'$ with respect to $\xi$. Integrating Eq (2.3) with respect to $\xi$ gives $Q_1(U, U', \dots) = 0$.

Step 2. Assume that the traveling wave solution to the ODE (2.3) is written as a polynomial in $(w/g)$ as follows:

where both functions $w = w(\xi)$ and $g(\xi)$ must satisfy the following auxiliary ODE of first order:

where the expansion coefficients $a_{i}\; (i = 0, 1, 2, \dots, m)$ and the arbitrary constants $a, b,$ and $c$ are to be further determined.

Step 3. The integer $m$ in Eq (2.4) is determined by balancing the nonlinear terms and the highest-order derivatives of $U(\xi)$ appearing in the ODE (2.3).

Step 4. Substitute the solution given by Eq (2.4) and the first-order equation given by Eq (2.5) into the ODE (2.3); the result implies that the left-hand side of the ODE (2.3) becomes a polynomial in $(w/g)$. In this polynomial, we equate each coefficient to zero to obtain a system of algebraic equations for $a_i$ and $k.$

Step 5. The obtained algebraic equations are solved with the aid of Mathematica or Maple, via which we find $a_i$ and $k$.

3.   Extended rational ($w/g$)-expansion method and its application

The extended rational ($w/g$)-expansion method, introduced by Li et al. ^[48], when applied to very important nonlinear evolution equations in many physical or engineering modeling problems, provides a computational shortcut to obtaining desired solutions of complex systems. This approach is based on the assumption that states that the exact solutions are written in the form of a polynomial in $(w/g)^i$ for $i = 0, 1, 2, \dots, m)$; also, both functions, $w$ and $g,$ must satisfy the following equation:

where $a, b,$ and $c$ are arbitrary constants. By choosing appropriate values for the functions $w$ and $g$, we obtain different powerful, new suitable methods that have been previously introduced.

The key aim of this section is to demonstrate the validity and advantages of the three expansion methods, namely, the $(g'/g^2)$-expansion method, $(g')$-expansion method, and the generalized simple $(w/g)$-expansion method by exploring new optical solitary wave solutions for nonlinear evolution equations through the use of the GZEs in Eq (1.2).

For the purpose of discussion, we investigate the GZEs in Eq (1.2). Since $\psi(x, t)$ in Eq (1.2) is a complex function, we assume that the traveling wave solutions can be expressed in the following form:

where $U(\xi)$ and $V(\xi)$ are real functions and $p, q,$ and $k$ are arbitrary constants. By substituting Eq (3.2) into the GZEs in Eq (1.2), we obtain

Integrating the second equation of Eq (3.3) twice with respect to $\xi$ and setting the first integration constant to zero, for simplicity, we obtain

where $C$ is the second integration constant. By substituting Eq (3.4) into the first equation of Eq (3.3), we obtain

To explore the solitary solutions of the above equation and investigate their physical properties, the following sections present three interesting analytical methods.

3.1.   On solving the GZEs by using the modified $(g'/g^{2})$-expansion method

The principle aim of this section is to explore the solitary solutions of the GZEs in Eq (1.2) by implementing the method of modified $(g'/g^{2})$-expansion. By setting the function $w = g'/g$ and the constant $b = 0$ in Eq (3.1), we obtain a new expansion in the following form:

where the expansion coefficients denoted by'n0ytg$a_{i}$ are constants to be further determined; the function $g(\xi)$ admits the following NLPDE:

hence, this is known as the $(g'/g^{2})$-expansion method, as introduced in ^[48]. By explicitly taking advantage of the homogeneous balance principle ^[52] between the higher-order nonlinear term $U^3$ and higher-derivative term $U^{\prime \prime}$ in Eq (3.5), we obtain the balance constant $m = 1$. Therefore, Eq (3.5) has a solution in the following form:

where $a_{0}$ and $a_{1}$ are arbitrary real constants to be further determined so that $g(\xi)$ satisfies Eq (3.7). Substituting Eqs (3.7) and (3.8) into Eq (3.5) implies that the left-hand side of Eq (3.5) becomes a polynomial in ($g'/g^{2}$). In this polynomial, we equate each coefficient to zero to obtain a system of algebraic equations for $a_{0}, a_{1},$ and $C$, which are addressed by using Mathematica software to obtain the following:

where $\omega = \left(4\lambda p^2-\lambda +1\right)\left(4p^2-1\right)$ and $k, \lambda, p, q, c, a$ are real constants to be further determined. Therefore, Eq (3.7) has general solutions in the following form for some constants $A$ and $B$:

The corresponding fields represented by $(g'/g^{2})$ are as follows:

Hence, three cases can be applied to determine the new types of solitary wave solutions to the GZEs in Eq (1.2):

Case 1. When $ca > 0$, we obtain a trigonometric function solution in the following form:

Substituting this equation into Eqs (3.2) and (3.4), we obtain solutions to the GZEs in Eq (1.2) as follows:

and

Case 2. When $ca < 0$, we obtain a solution in the following form:

Substituting this equation into Eqs (3.2) and (3.4), we obtain the solutions to the GZEs in Eq (1.2) as follows:

and

Case 3. When $a = 0$ and $c\ne 0$, we obtain a rational function solution in the following form:

Substituting this equation into Eqs (3.2) and (3.4), we find the solutions of the GZEs in Eq (1.2) as follows:

and

3.2.   On solving the GZEs by using the modified $(g')$-expansion method

Here, we adopt an efficient technique, namely the modified $(g')$-expansion method to explore the traveling wave solutions of the GZEs in Eq (1.2). By setting the function $w = gg'$ and the constant $b = 0$ in Eq (3.1), we obtain a new expansion in the following form:

where the expansion coefficients denoted by $a_{i}$ are constants to be further determined and the function $g(\xi)$ admits the following NLPDE:

hence, this is known as the $(g')$-expansion method, as introduced in ^[48,53]. Using the homogeneous balance principle between the higher-order nonlinear term $U^3$ and higher-derivative term $U^{\prime \prime}$ in Eq (3.5), we obtain the balance constant $m = 1$. Therefore, Eq (3.5) has a solution in the following form:

where $a_{0}$ and $a_{1}$ are constants and $g(\xi)$ satisfies Eq (3.15). Substituting Eqs (3.15) and (3.16) into Eq (3.5) implies that the left-hand side of Eq (3.5) becomes a polynomial in $g'$. In this polynomial, we equate each coefficient to zero to obtain a system of algebraic equations for $a_{0}, a_{1},$ and $C$, which are solved by using Mathematica software to obtain the following:

where $k, \lambda, p, q, c, a,$ and $b$ are arbitrary constants. The general solutions of Eq (3.15) are given as follows:

The corresponding derivative fields are as follows:

Hence, three cases can be applied to determine the new types of solitary wave solutions for the GZEs in Eq (1.2):

Case 1. If $\Delta = 4ac-b^{2} > 0$, the solitary wave solution of Eq (3.5) is given by

Substituting the above equation into Eqs (3.2) and (3.4), we find the solutions to the GZEs in Eq (1.2) as follows:

and

Case 2. If $\Delta = 4ac-b^{2} < 0$, the solitary wave solution of Eq (3.5) is given by

Substituting the above equation into Eqs (3.2) and (3.4), we find the solutions to the GZEs in Eq (1.2) as follows:

and

Case 3. If $\Delta = 4ac-b^{2} = 0$, the solitary wave solution of Eq (3.5) is given by

Substituting the above equation into Eqs (3.2) and (3.4), we find the solutions to the GZEs in Eq (1.2) as follows:

and

3.3.   On solving the GZEs by using the generalized simple ($w/g$)-expansion method

In this subsection, the generalized simple ($w/g$)-expansion method is employed to investigate the exact solutions and then explore the solitary wave solutions for Eq (3.5). A new form of exact solutions can be obtained as follows

where the expansion coefficients denoted by $a_{i}$ are arbitrary constants. The functions $w$ and $g$ satisfy the conditions of the following coupled system of differential equations:

where $\lambda$ and $\mu$ are arbitrary constants. This is known as the generalized simple ($w/g$)-expansion method. By balancing the highest-order derivative and the nonlinear term in Eq (3.5) by using the homogeneous balance method, we obtain the balance constant $m = 1$. Therefore, Eq (3.5) has a solution which can be written as follows:

where $a_{0}$ and $a_{1}$ are constants so that $w(\xi)$ and $g(\xi)$ satisfy Eq (3.23). Substituting Eqs (3.23) and (3.24) into Eq (3.5) implies that the left-hand side of Eq (3.5) becomes a polynomial in (${w}/{g}$). In this polynomial, we equate each coefficient to zero to obtain a system of algebraic equations for $a_{0}, a_{1},$ and $C$, which are solved by using Mathematica software to obtain the following:

where $k, \lambda,$ and $\mu$ are constants. Hence, Eq (3.23) has a general solution in the following form:

where $A$ and $B$ are arbitrary constants. Four cases can be applied to determine the new types of solitary wave solutions for the GZEs in Eq (1.2):

Case 1. If $\lambda > 0$ and $\mu > 0$, we can find a hyperbolic function solution of Eq (3.5) in the following form:

Substituting the above equation into Eqs (3.2) and (3.4), we can find the solution to the GZEs in Eq (1.2) as follows:

and

Case 2. If $\lambda < 0$ and $\mu < 0$, we can find the solitary wave solution of Eq (3.5) which can be written in the following form:

Substituting the above equation into Eqs (3.2) and (3.4) we find the solution to the GZEs in Eq (1.2) as follows:

and

Case 3. If $\lambda > 0$ and $\mu < 0$, we can obtain a trigonometric function solution of Eq (3.5) in the following form:

Substituting the above equation into Eqs (3.2) and (3.4), we can find the solution to the GZEs in Eq (1.2) as follows:

and

Case 4. If $\lambda > 0$ and $\mu < 0$, we can obtain the periodic wave solution of Eq (3.5) in the following form:

Substituting the above equation into Eqs (3.2) and (3.4) we find the solution to the GZEs in Eq (1.2) as follows:

and

Remark 1. ^[48] Setting the constant coefficients $c = 1$ and $b = 0$ and the function $g = 0$ in Eq (3.1), we can obtain a new expansion in the following form:

which are identical to the tanh-function approach; thus, it follows that the expansion coefficients denoted by $a_{i}$ are arbitrary constants and the function $w(\xi)$ satisfies the following equation:

Meanwhile, when the constant coefficients $a = b = c \ne 0$ and the function $g = 1$, the expansion given by Eq (2.4) becomes identical to the Riccati expansion ^[54,55].

Remark 2. ^[48,53] Setting the constant coefficients $a = -\mu, b = -\lambda,$ and $c = -1$ and the function $w = g'$ in Eq (3.1) yields a new expansion in the following form:

which is identical to the $(G'/G)$-expansion method introduced in ^[47]; thus, the expansion coefficients denoted by $a_{i}$ are constants and the function $g(\xi)$ satisfies Eq (1.3).

4.   AKM and its application

The Kudryashov method was introduced by Kudryashov ^[49] to efficiently compute and predict the highly dispersive optical solitons of some NLPDEs that arise in different applications. In this scheme, the calculations are performed without using a specific function's form. Inspired by the Kudryashov method, many powerful and efficient methods have been developed over the last few years to find the exact solutions of some NLPDEs. Examples of such methods include the generalized Kudryashov's method ^[18], the extended Kudryashov's method ^[56], and the new extended generalized Kudryashov's method ^[57]. In addition, among these techniques, we should mention the AKM method which was introduced by Zayed et al. ^[50]. This method is an efficient technique for obtaining exact solutions to the NLPDEs. The objective of the following sections is to implement this approach to explore different types of solitary wave solutions to the GZEs in Eq (1.2). For convenience, the following section starts by presenting the basic steps of the implemented method.

4.1.   Methodology

In this section, we briefly present the basic steps of the AKM as follows:

Step 1. Let us assume that Eq (3.5) has a solution in the following form:

where the expansion coefficients denoted by $b_{i}$ are constants for $i = 0, 1, \dots, M$; thus, the function $R(\xi)$ admits the following equation:

where $k$ is a positive number, with $k \neq 1$, and $\chi$ is an arbitrary constant. The solution of Eq (4.2) is written as follows:

Here, $b$ and $T$ represent a non-zero real number and a natural number, respectively; also note the function $\exp_{K}(T\xi) = K^{T\xi }$.

Step 2. To determine the relation between $M$ and $T$, we consider the following formula:

Let us assume that the function $F[\phi (\xi)] = M$; hence, $F[\phi ^{^{\prime }}(\xi)] = M+T$ and $F [\phi ^{^{\prime \prime }}(\xi)] = M+2T$.

Therefore, $F[\phi ^{(r)}(\xi)] = M+rT$ and $F[\phi ^{(r)}(\xi)\ \phi ^{s}(\xi)] = (s+1)M+rT.$

Step 3. Substitute Eqs (4.1) and (4.2) into Eq (3.5); then, set each coefficient of the following term to zero:

resulting in a set of algebraic equations in $b_{i}$ for $i = 0, 1, 2, \dots, M.$ These equations can be addressed to determine $b_i$ and $c$. Hence, the analytical solutions to Eq (3.5) can be obtained.

4.2.   On solving the GZEs by using the AKM

Here, we aim to find new solitary wave solutions for nonlinear evolution equations by implementing the AKM. By balancing the nonlinear terms $U^{^{\prime \prime }}$ and $U^{3}$ in Eq (3.5), we obtain

Two scenarios are presented here to determine the new types of solitary wave solutions to the GZEs in Eq (1.2):

Case 1. Choosing $T = 1$ gives $M = 1.$ Therefore, Eq (3.5) has a solution in the following form:

where $b_{0}$ and $b_{1}$ are arbitrary constants such that $b_{1}\neq 0.$ Substitute Eqs (4.1) and (4.5) into Eq (3.5); then, we can equate each coefficient to zero

This procedure yields a system of algebraic equations as follows:

The above equations are solved to obtain

Substituting Eqs (4.6) and (4.3) into Eq (4.5), we can obtain the straddled solitary solutions of the GZEs in Eq (1.2) as follows:

and

It follows that $\chi (1-4p^{2})(4\lambda p^{2}-\lambda +1) > 0.$

Remark 3. Setting $\chi = 4b^{2}$ in Eqs (4.7) and (4.8) yields the bright soliton solutions to the GZEs in Eq (1.2) as follows:

It follows that $(1-4p^{2})(4\lambda p^{2}-\lambda +1) > 0.$ Meanwhile, setting $\chi = -4b^{2}$ in Eqs (4.7) and (4.8) yields the singular soliton solutions to the GZEs in Eq (1.2) as follows:

It follows that $(4p^{2}-1)(4\lambda p^{2}-\lambda +1) > 0.$

Case 2. Choosing $T = 2$ gives $M = 2.$ Therefore, Eq (3.5) has a solution in the form:

where $b_{0}, b_{1},$ and $b_{2}$ are constants to be determined such that $b_{2}\neq 0.$ Substitute Eqs (4.1) and (4.13) into Eq (3.5); then, we can equate each coefficient to zero

This procedure yields a system of algebraic equations which can be solved to get the following results:

Substituting Eqs (4.3) and (4.14) into Eq (4.13), we can calculate the straddled solitary solution of the GZEs in Eq (1.2) as follows:

It follows that $\chi (1-4p^{2})(4\lambda p^{2}-\lambda +1) > 0.$

Remark 4. Setting $\chi = 4b^{2}$ in Eqs (4.15) and (4.16) yields the bright soliton solution to the GZEs in Eq (1.2) as follows:

It follows that $(1-4p^{2})(4\lambda p^{2}-\lambda +1) > 0.$ Meanwhile, setting $\chi = -4b^{2}$ in Eqs (4.15) and (4.16) yields the singular soliton solutions to the GZEs in Eq (1.2) as follows:

It follows that $(4p^{2}-1)(4\lambda p^{2}-\lambda +1) > 0.$ It is worth mentioning that, by varying the values of the parameters $T$ and $M$, we can obtain a variety of solitary wave solutions to the GZEs in Eq (1.2). For the purpose of checking, we verify that all of the obtained results satisfy the GZEs in Eq (1.2).

5.   Graphical representation of the obtained solitary wave solutions for the GZEs

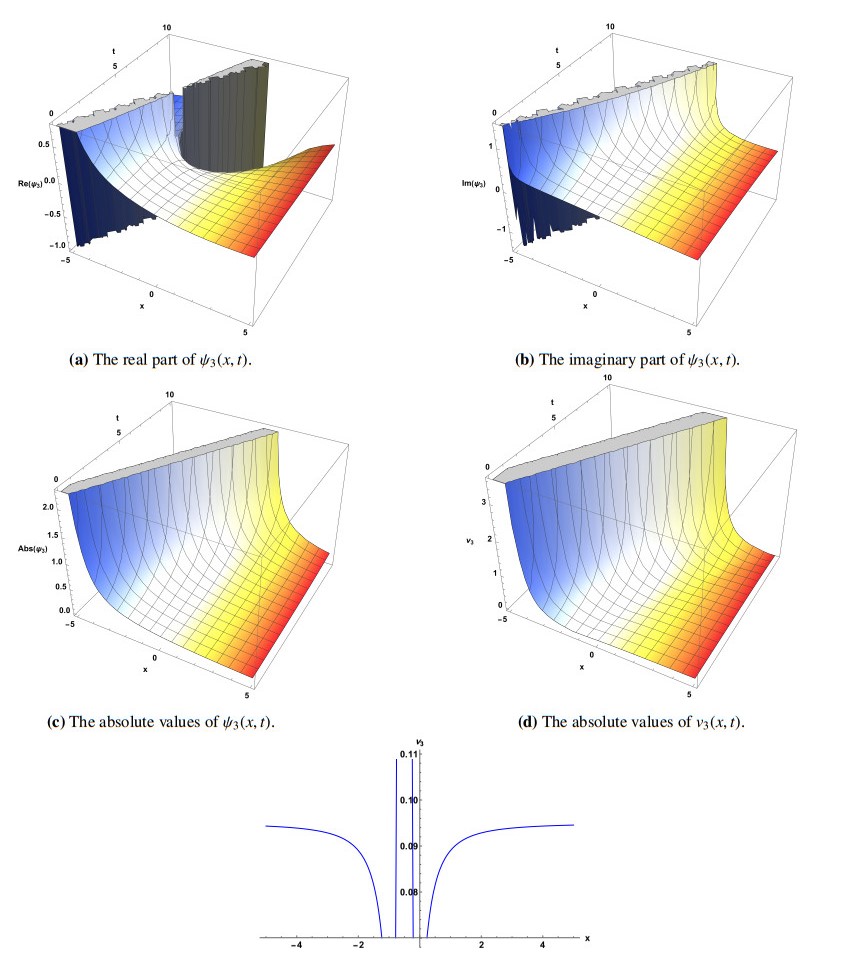
The GZE is an important model equation in mathematical physics because the derived solutions are particularly useful for modeling different types of Langmuir wave propagation, such as those applied in the field of plasma physics. In solitary wave theory, there are numerous forms of traveling wave solutions that are very interesting to investigate. In this paper, we present different types of traveling wave solutions that have been obtained based on the explicit solutions in Eqs (3.9)–(4.18) when physical parameters are given certain values.

The principle aim of this section is to present graphical illustrations of multiple solitary wave solutions of the GZEs in Eq (1.2) that can be obtained by using the methods discussed in Sections 3 and 4. The obtained solutions have been plotted to facilitate comprehension of the physical principles and efficacy of the used methods. In soliton physics, solitons are localized waves that propagate without changing their shape or velocity, and they are considered one type of solitary waves that are used to describe a wide range of nonlinear physical phenomena, including the propagation of solitons in optical fibers. Particle-like structures like magnetic monopoles and other similar structures can also arise from soliton solutions. Hence, soliton wave solutions may be necessary to obtain comprehension of both the complex and naturally physical properties of the constructed topological, singular soliton, and singular periodic wave solutions.

Solutions $\psi_{3}(x, t)$, $\psi_{6}(x, t)$, and $\psi_{13}(x, t)$ of the GZEs represent singular soliton solutions. Solitary waves with a singularity are referred to as singular soliton solutions. Solutions of $\psi_{5}(x, t)$, $\psi_{8}(x, t)$, and $\psi_{12}(x, t)$ represent the exact solitary wave solution of bright soliton type under different physical parameter conditions. Since the natures of some obtained solutions are identical, and for convenience, we have only plotted some interesting solutions as shown in the following figures. Since the envelope $\psi (x, t)$ is a complex function, we characterize the solitary wave propagation for various instances by using $|\psi (x, t)|$. Figures 1–6 present the real and imaginary parts and the absolute values of the obtained complex function $\psi(x, t)$, the absolute value of $v(x, t)$ and its projection at $t = 0$. Figure 1 depicts the solutions of Eq (3.13). The $3$D figure is portrayed within the interval $-5 \leq x \leq 5.$ It is clear that the dynamic behaviors in this figure show an example of singular wave solutions for the GZEs in Eq (1.2) which were successfully obtained by using the modified $(g'/g^2)$-expansion method in Section 3.1. Singular solitons are associated with solitary waves when the solitary wave's center position is imaginary. Note that a singularity commonly appears in the presence of rational or trigonometric functions.

The results for the bright solitons can be seen in Figure 2 for the wave solutions of Eq (3.19), which were obtained by means of the $(g')$-expansion method. Moreover, Figure 3 presents the dynamic behaviors of the wave solutions of Eq (3.21), which were also obtained by using the $(g')$-expansion method. The bright solitary wave solutions are also shown in Figure 4, and they were determined by using the generalized simple $(w/g)$-expansion method (Section 3.3). Figures 5 and 6 depict the physical behaviors of the obtained solutions given by Eqs (4.9) and (4.11), which were obtained by using the AKM. It can be observed that the contour of the absolute value plot is a perfect bright wave; however, as for the real and imaginary parts, they are all kinky bright waves as shown in Figure 5. Notice that, if both real and imaginary parts exhibit the bright wave characteristic, we refer to them as rough bright waves. Figure 6 presents the exact singular soliton solutions. It can be observed that, from all of the listed figures we can see that the AKM is more accurate, very effective and easier than other methods purposed to capture the physical behavior of the obtained solutions.

6.   Conclusions

In many applications, physical phenomena can be accurately modeled and described by using NLPDE. Examples of such applications include nonlinear chaotic systems, heat conduction systems, diffusion processes, plasma waves, and chemical physics. This paper served to achieve two aims: First, new solitary wave solutions for a set of coupled equations that is widely used as a realistic model in the field of plasma physics have been discovered by employing four schemes of integration. The second aim of this paper has been achieved by evaluating the effectiveness and reliability of the constructed schemes on GZEs. Therefore, this should empower us, with great flexibility, to expand the applicability of these methods to a wide range of physical problems of special interest. It should be emphasized that the obtained results significantly help to better understand and describe the nonlinear physical phenomena that arise in different fields, including fluid dynamics, quantum mechanics, optical fibers, and plasma physics. These methods can contribute to significantly reduce the computation time for complex systems through the use of computer algebra systems, such as Maple or Mathematica, which can replace much tedious manual calculations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author extends his appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-92).

Funding

This research was funded by Taif University, Saudi Arabia, Project No. (TU-DSPP-2024-92).

Conflict of interest

The author declares no conflict of interest.