Milne-Type inequalities via expanded fractional operators: A comparative study with different types of functions

1.   Introduction

Fractional calculus has attracted significant attention from scholars because of its extensive applications in both theoretical and applied mathematics, as highlighted in various sources ^[1,2]. The fractional integral and derivative have no one representation, like the conventional integral and derivative; rather, representations change throughout time and across writers. It is well known that one of the most important research tools in mathematics is the inequality. Fractional inequalities, particularly those associated with Jensen, Hermite-Hadamard, and Simpson, constitute a significant and multifaceted field in mathematical analysis ^[3,4,5,6]. Each of these inequalities provides valuable insights into the relationships governed by fractional calculus, contributing to a nuanced comprehension of functions and their integral properties.

Jensen's fractional inequality, which is an extension of the classical Jensen's inequality, investigates the convexity aspects of fractional integrals. It provides bounds on the fractional integral of a convex function, with applications spanning the probability theory, statistics, and diverse mathematical branches. Jensen's fractional inequality enhances our understanding of integral behavior for convex functions; see ^[7,8].

The Hermite-Hadamard fractional inequality, pioneered by Hermite and later expanded by Hadamard, serves as a fundamental tool for exploring the convexity of functions and its extensions. This inequality establishes bounds on the integral mean of a function, offering connections between convexity and fractional calculus; see ^[9,10,11].

Simpson's fractional inequality, a derivative of the classical Simpson's inequality, extends the exploration of inequalities into fractional calculus. It facilitates the estimation of the integral mean of a function based on its values at multiple points. Simpson's fractional inequality proves to be a valuable analytical tool, akin to its classical counterpart, shedding light on the behavior of functions and their fractional integrals; see ^{[12,13,14,15,16,17,18,19]}.

Fractional analysis is an ever-evolving field striving for continual innovation to provide solutions to the evolving challenges of the world ^[20]. Numerous fractional derivative and integral operators have been introduced since the inception of fractional analysis. Several of these operators hold significant importance in problem-solving within applied mathematics and analysis. Notable examples include Riemann-Liouville, expanded fractional integral operators, Caputo, Hadamard, Erdelyi-Kober, Marchaud, and Riesz, among others. Within fractional calculus, fractional derivatives are formulated through fractional integrals ^{[21,22,23,24]}. One particularly important and practical fractional integral operator is known as Riemann-Liouville fractional integrals, which can be defined as follows.

Definition 1.1. Let $\mathfrak{Z}\in L_{1}[\lambda _{1}, \lambda _{2}].$ The Riemann-Liouville fractional integrals $\mathfrak{I}_{\lambda _{1}+}^{\sigma_1 }\mathfrak{Z}$ and $\mathfrak{I}_{\lambda _{2}-}^{\sigma_1 }\mathfrak{Z}$ of order $\sigma_1 > 0$ are defined by

and

respectively. Here, $\Gamma (\sigma_1) = \int_0^\infty q^{\sigma_1-1}e^{-q} dq$ is the Gamma function and $\mathfrak{I }_{\lambda _{1}+}^{0}\mathfrak{Z}(p) = \mathfrak{I}_{\lambda _{2}-}^{0} \mathfrak{Z}(p) = \mathfrak{Z}(p).$

For more information about Riemann-Liouville fractional integrals, please refer to ^[22,25,26].

We recall Beta function (see, e.g., [27, Section 1.1])

and the incomplete gamma function, defined for real numbers $a > 0$ and $x\geq0$ by

Jarad et. al. ^[21] introduced a novel fractional integral operator, which called generalized fractional integral operators. Also, they gave some properties and relations between some other fractional integral operators, such as the Riemann-Liouville fractional integral and Hadamard fractional integrals.

Let $\sigma_2 \in \mathbb{C}, \, \, Re(\sigma_2) > 0$, then the left and right-sided fractional generalized integral operators are defined, respectively, as follows:

A formal definition for convex function may be stated as follows:

Definition 1.2. ^[28] Let $I$ be a convex set on $\mathbb{R}$. The function $\mathfrak{Z}:I\rightarrow \mathbb{R}$ is called convex on $I$ if it satisfies the following inequality:

for all $(p, \gamma)\in I$ and $q\in \lbrack 0, 1].\ $The mapping $\mathfrak{Z}$ is a concave on $I$ if the inequality (1.6) holds in reversed direction for all $q\in \lbrack 0, 1]$ and $p, \gamma \in I$.

The primary objective of this research is to derive some Milne-type inequalities applicable with specific function classes through the utilization of expanded fractional integral operators (1.4) and (1.5). This study focuses on establishing a fundamental equality associated with the fractional expanded integral operators, thereby presenting various Milne-type inequalities applicable to functions with convex derivatives (FCD). Additionally, we give an illustrative example to elucidate the acquired outcomes. By employing the fractional expanded integrals, we explore some Milne-type inequalities for bounded and Lipschitzian functions. Moreover, this study deals with Milne-type inequalities, including functions of bounded variation.

This paper is divided to six sections, starting with an introduction. In Section 2, we establish a crucial equality using fractional expanded integral operators. This equality forms the basis for proving Milne-type inequalities for FCD, backed by illustrative examples. Sections 3 and 4 explore Milne-type inequalities for bounded and Lipschitzian functions, respectively. Section 5 focuses on Milne-type inequalities for functions of bounded variation. Lastly, Section 6 encapsulates the research conclusions.

2.   Milne-type inequalities for FCD

Here, we showcase several Milne-type inequalities pertaining to FCD.

Lemma 2.1. Let $\mathfrak{Z}:[\lambda _{1}, \lambda _{2}]\rightarrow \mathbb{R}$ be a differentiable mapping $(\lambda _{1}, \lambda _{2})$ such that $\mathfrak{Z}^{\prime }\in L_{1}\left(\left[\lambda _{1}, \lambda _{2}\right] \right)$. The subsequent equation is true:

where $\sigma_1, \sigma_2 > 0$, $B(\sigma_1, \sigma_2)$ and $\Gamma$ are Euler Beta and Gamma functions, respectively.

Proof. Through the application of integration by parts, we obtain

Similarly, we obtain

From the equalities (2.1) and (2.2), the ensuing outcome is achieved:

So, Lemma 2.1 has been proven. □

Theorem 2.1. Suppose the assumptions stipulated in Lemma 2.1 are valid and the function $\left \vert \mathfrak{Z}^{\prime }\right \vert$ is convex on $\left[\lambda _{1}, \lambda _{2}\right]$, then we obtain the subsequent inequality.

where $\sigma_1, \sigma_2 > 0$, $B(\sigma_1, \sigma_2)$, and $\Gamma$ are Euler Beta and Gamma functions, respectively.

Proof. Applying the absolute value to Lemma 2.1 and leveraging the convexity of $\left \vert \mathfrak{Z}^{\prime }\right \vert$, we obtain:

Therefore, we achieve the intended result. □

Remark 2.1. If we choose $\sigma_1 = 1$ in Theorem 2.1, the ensuing Milne-type inequality holds for Riemann-Liouville fractional integrals.

Theorem 2.2. Assuming the conditions stipulated in Lemma 2.1 are met, and considering that the mapping $\left \vert \mathfrak{Z}^{\prime }\right \vert ^{y}$, where $y > 1$, exhibits convexity on the interval $[\lambda _{1}, \lambda _{2}]$, the ensuing inequality holds:

where $\frac{1}{x}+\frac{1}{y} = 1$, $\sigma_1, \sigma_2 > 0$, $B(\sigma_1, \sigma_2)$, and $\Gamma$ are Euler Beta and Gamma functions, respectively.

Proof. When we compute the absolute value of Lemma 2.1, the outcome is:

By leveraging the "H"older inequality within inequality (2.5) and capitalizing on the convexity of $\left \vert \mathfrak{Z}^{\prime }\right \vert ^{y}$, we get

Likewise, we can arrive at the inequality

By substituting (2.6) and (2.7) in (2.5), we have

Hence, the first inequality in Eq (2.4) has been successfully derived. Now, let's move forward with proving the second inequality. Let $\alpha_{1} = 3\left \vert \mathfrak{Z}^{\prime }\left(\lambda _{1}\right) \right \vert ^{y},$ $\beta_{1} = \left \vert \mathfrak{Z}^{\prime }\left(\lambda _{2}\right) \right \vert ^{y},$ $\alpha_{2} = \left \vert \mathfrak{Z }^{\prime }\left(\lambda _{1}\right) \right \vert ^{y}$, and $\beta_{2} = 3\left \vert \mathfrak{Z}^{\prime }\left(\lambda _{2}\right) \right \vert ^{y}.$ By leveraging the facts that

and $1+3^{\frac{1}{y}}\leq 4$, the desired outcome may be determined right away, and Theorem 2.2 has been fully proven. □

Remark 2.2. If we choose $\sigma_1 = 1$ in Theorem 2.2, the following Milne-type inequality for Riemann-Liouville fractional integrals is derived:

Theorem 2.3. Assuming all the conditions of Lemma 2.1 are met, when the function $\left \vert \mathfrak{Z}^{\prime }\right \vert ^{y}$, where $y\geq 1$, demonstrates convex behavior over the interval $[\lambda _{1}, \lambda _{2}]$, we get the subsequent inequality:

where $\sigma_1, \sigma_2 > 0$, $B(\sigma_1, \sigma_2)$ and $\Gamma$ are Euler Beta and Gamma functions, respectively.

Proof. By employing the power-mean inequality in (2.5) and taking into account the convex nature of $\left \vert \mathfrak{Z}^{\prime }\right \vert ^{y}$, we arrive at:

By a similar method used in (2.9), we have

Substituting (2.9) and (2.10) in (2.5), we get

This completes the proof. □

Remark 2.3. If we choose $\sigma_1 = 1$ in Theorem 2.3, then we have the following Milne-type inequality for Riemann-Liouville fractional integrals

Example 2.1. Consider the function $\mathfrak{Z}:\left[2, 4\right] \rightarrow \mathbb{R},$ $\mathfrak{Z}(q) = \frac{q^{3}}{3}.$ It is clear that $\left \vert \mathfrak{ \mathfrak{Z}}^{\prime }\right \vert$ is convex on $\left[2, 4\right]$, then we have

By (1.4), we have

and similarly by (1.5), we have

Hence, the computation of the left term in the inequalities (2.3), (2.4), and (2.8) results in:

Conversely, the right term in the inequality (2.3) is expressed as:

Similarly, for $y = 2$, the right sides of the inequalities (2.4) and (2.8) reduce to

and

respectively. Consequently, we have the following inequalities from (2.4) and (2.8)

and

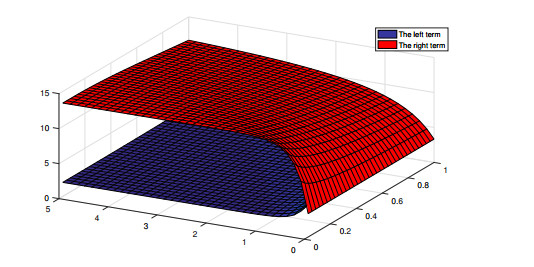
respectively. One can see the validity of the inequalities (2.11), (2.12), and (2.13) in Figures 1–3, respectively.

3.   Milne-type inequality for bounded functions

Theorem 3.1. Assume that the conditions of Lemma 2.1 hold. If there exist $\omega, \Omega\in \mathbb{R}$ such that $\omega\leq \mathfrak{Z}^{\prime }(q)\leq \Omega$ for $q\in \left[\lambda _{1}, \lambda _{2}\right],$ then we establish

where $\sigma_1, \sigma_2 > 0$, $B(\sigma_1, \sigma_2)$, and $\Gamma$ are Euler Beta and Gamma functions, respectively.

Proof. With the help of Lemma 2.1, we get

By considering the absolute value of (3.1), we obtain:

From $\omega\leq \mathfrak{Z}^{\prime }(q)\leq \Omega$ for $q\in \left[\lambda _{1}, \lambda _{2}\right],$ we get

and

Using (3.2) and (3.3), we have

The proof of the theorem is finished. □

Remark 3.1. If we choose $\sigma_1 = 1$ in Theorem 3.1, then we have the following Milne-type inequality for Riemann-Liouville fractional integrals

4.   Milne-type inequality for Lipschitzian functions

In this section, we introduce some fractional Milne-type inequalities applicable to Lipschitzian functions.

Theorem 4.1. Suppose that the assumptions of Lemma 2.1 hold. If $\mathfrak{Z}^{\prime }$ is a $L$-Lipschitzian function on $\left[\lambda _{1}, \lambda _{2}\right],$ then the result yields the subsequent inequality:

where $\sigma_1, \sigma_2 > 0$, $B(\sigma_1, \sigma_2)$, and $\Gamma$ are Euler Beta and Gamma functions, respectively.

Proof. With help of Lemma 2.1, since $\mathfrak{Z}^{\prime }$ is $L$ -Lipschitzian function, we get

This concludes the proof of this theorem. □

Remark 4.1. If we choose $\sigma_1 = 1$ in Theorem 4.1 then the following Milne-type inequality for Riemann-Liouville fractional integrals is established:

5.   Milne-type inequality for functions of bounded variation

In this section, we demonstrate a Milne-type inequality using expanded fractional integrals of bounded variation.

Theorem 5.1. Let $\mathfrak{Z}:\left[\lambda _{1}, \lambda _{2}\right] \rightarrow \mathbb{R}$ be a mapping of bounded variation on $\left[\lambda _{1}, \lambda _{2}\right],$ then we get

where $\sigma_1, \sigma_2 > 0$, $B(\sigma_1, \sigma_2)$, and $\Gamma$ are Euler Beta and Gamma functions and $\bigvee \limits_{c}^{d}(\mathfrak{Z})$ demonstrates the total variation of $\mathfrak{Z}$ on $\left[c, d\right].$

Proof. Define the function $K_{\sigma_1 }^{\sigma_2 }(p)$ by

then we have

By applying integration by parts, the result is

and, similarly,

By (5.1) and (5.2), we have

That is,

It is well known that if $g, \mathfrak{Z}:\left[\lambda _{1}, \lambda _{2} \right] \rightarrow \mathbb{R}$ are such that $g$ is continuous on $\left[\lambda _{1}, \lambda _{2}\right]$ and $\mathfrak{Z}$ is of bounded variation on $\left[\lambda _{1}, \lambda _{2} \right]$, then $\int \limits_{\lambda _{1}}^{\lambda _{2}}g(q)d\mathfrak{Z}(q)$ exists and

Otherwise, utilizing (5.3), we have

This finishes the proof. □

Remark 5.1. If we choose $\sigma_1 = 1$ in Theorem 5.1, then we have the following Milne-type inequality for Riemann-Liouville fractional integrals

6.   Conclusions

This research effectively demonstrated Milne-type inequalities across various types of functions using expanded fractional integral operators. By establishing an important equality connected to these operators, we uncovered several Milne-type inequalities that apply to FCDs. To illustrate these discoveries, we provided an example. Additionally, we investigated Milne-type inequalities for bounded and Lipschitzian functions using fractional expanded integrals. Finally, we extended our study to include Milne-type inequalities for functions with bounded variation.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Research Groups Program under grant RGP.2/102/44.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this article.