1.
Introduction
The use of probability distributions has been ages old in many areas of life. The probability distributions provide a way to model phenomenon in many fields that ranges from economics to finance and from physical sciences to astronomy. Various standard probability distributions are available that can be used to model various real-life phenomenon, but in several situations these standard probability distributions fail to capture the underlying trend of the data. In such situations, some extensions or generalizations are required. A method to extend any baseline probability distribution has been proposed by [1] by using the logit of beta distribution. Another simple method to extend any baseline distribution has been proposed by [2] and is known as the transmuted family of distribution. The cumulative distribution function (cdf) of this family of distributions is
where G(x) is the cdf of any baseline distribution and λ is the transmutation parameter such that −1≤λ≤1. The transmuted family of distributions has been explored by various authors for different baseline distributions, see for example [3].
A general method of obtaining new families of distributions has been proposed by [4] by using two probability distributions. The proposed family of distributions is named as the T-X family of distributions. The cdf of the proposed family of distributions is
where r(t) is density function of some random variable t with support on [a,b] and W[G(x)] is some function of G(x) such that W(0)→a and W(1)→b. The T-X family of distributions gives rise to several other families of distributions as a special case. The transmuted family of distributions can be obtained from the T-X family of distribution by using r(t)=1+λ−2λt;t∈[0,1] and W[G(x)]=G(x) as shown by [5].
Several situations arise where we are interested in joint modeling of two or more than two random variables. For example, we might be interested in simultaneous modeling of computer memory and processing time or we might be interested in joint modeling of various characteristics of plants. In such situations the bivariate and/or the multivariate distributions are needed. The development of bivariate distributions has attracted various authors but in most of the situations the bivariate and/or multivariate distributions are not unique. A simple way of obtaining the bivariate distributions from the univariate marginals has been proposed by [6] and is known as the Gumbel bivariate distributions. The joint cdf of this family of distributions is
where G1(x) and G2(y) are marginal cdf's of X and Y respectively and γ is a measure of association such that −1≤γ≤1. The bivariate Gumbel distribution (3) has been used by various authors to propose some new bivariate distributions, see for example [7,8,9].
Another method of generating the bivariate distributions from the univariate marginals is given by [10]. The joint cdf of this family of bivariate distributions is
The bivariate family of distributions given in (4) includes the bivariate logistic distribution as a special case. The family of distributions given in (4) has not been studied in much details. The families of distributions given in (3) and (4) emerge by using the specialized technique of copulas. Further details about methods of generating bivariate and multivariate distributions by using copulas can be found in [11,12]. Some other bivariate families of distributions can be found in [13,14,15,16].
Recently, a new method has been proposed by [17] to obtain the bivariate families of distributions by obtaining the bivariate version of the T-X family of distributions. The joint cdf of the proposed bivariate T-X family of distributions is
where r(v1,v2) is some joint density function with support on [a1,b1]×[a2,b2]. Also, W1[G1(x)] and W2[G2(y)] are some absolutely continuous functions of G1(x) and G2(y) such that W1(0)→a1, W1(1)→b1, W2(0)→a2 and W2(1)→b2. A simpler version of the family (5) is given by [18] when the support of r(v1,v2) is [0,1]×[0,1]. The joint cdf in this case is given as
It can be seen that the Gumbel bivariate distribution can be obtained from (6) by using
The family of distributions given in (6) has been used by [18] to propose a new bivariate family of distributions which is a simpler version of the Cambanis family of distributions, proposed by [19]. The proposed family of distributions has also been used by [20] to propose a bivariate transmuted Burr distribution by using the Burr-XII distribution, proposed by [21], as the baseline distribution. In this paper we have proposed a new bivariate family of distributions by using the bivariate T-X family of distributions given in (6). The research motivation and plan of this paper are given in the following.
2.
Research motivation and plan of paper
It often happens that the joint modeling of two or more variables is required. For example, a computer scientist might be interested in joint modeling of processing time and processor speed. In such cases the bivariate and/or multivariate distributions are required. Not much work has been done in developing the bivariate and/or multivariate families of distributions and this research is motivated by this fact. The research will attempt to propose new bivariate and multivariate families of distributions for joint modeling of several random variables. The plan of the paper follows.
The new bivariate family of distributions is proposed in Section 3 and some of its properties are studied in Section 4. Section 5 is dedicated to the multivariate extension of the proposed family alongside some of its properties. In Section 6, a new bivariate Weibull distribution has been proposed by using the new bivariate family of distributions. Some properties of the proposed bivariate Weibull distribution are also studied in the same section. This section also contains a brief about a new multivariate Weibull distribution. Section 7 is reserved for simulation and real data applications of the proposed bivariate Weibull distribution. Conclusions and recommendations are given in Section 8.
3.
A new bivariate family of distributions
The bivariate family of distributions given in (6) can be used to obtain new bivariate families of distributions for different choices of r(v1,v2). Motivated by this fact, we have proposed a new bivariate family of distributions by using the following joint density of v1 and v2
in (6) such that the new bivariate family of distribution will provide flexibility to model more complex bivariate data. The joint cdf of the proposed bivariate family of distributions is
which on simplification becomes
for (x,y)∈R2. The parameters (λ1,λ2,λ3) satisfy the conditions
and
The joint cdf given in (7) can also be written as
where λ=λ1+λ2+λ3. The joint density function of the proposed bivariate family of distributions is easily obtained from (7) and is
The proposed bivariate family of distributions can be used to obtain new bivariate distributions for different baseline distributions G1(x) and G2(y). The marginal families of distributions of X and Y can be easily obtained from (7) and are
and
We can see that the marginal families of distributions are transmuted families.
The conditional families of distributions for X and Y can be easily obtained and are
and
where Δ1(y)=1+(λ2+λ3){1−2G2(y)} and Δ2(x)=1+(λ1+λ3){1−2G1(x)}. The marginal and conditional distributions can be studied for any baseline distribution.
4.
Properties of the new bivariate family of distributions
In this section we will discuss some properties of the proposed bivariate family of distributions. These properties are discussed in the following subsections.
4.1. Product and ratio moments
The moments of a random variable are useful in studying its properties. In case of joint distribution of two random variables the joint and ratio moments can be computed. The (r, s)th order joint moment of two random variables is defined as
Now, using the joint density function of X and Y, given in (8), the (r, s)th order joint moment for the proposed bivariate family of distributions is
which on simplification becomes
where μrX is rth raw moment of X, μsY is sth raw moment of Y, μrX(2:2) is rth raw moment of larger observation in a sample of size 2 from G1(x) and μsY(2:2) is sth raw moment of larger observation in a sample of size 2 from G2(y); see for example [22,23].
The ratio moments are also useful in some studies. The ratio moment for two random variables can be defined in two ways which are given as
Using the joint distribution of X and Y the ratio moments μrsX,Y and μsrX,Y are
and
where μ−rX is rth inverse moment of X, μ−sY is sth inverse moment of Y, μ−rX(2:2) is rth inverse moment of larger observation in a sample of size 2 from G1(x) and μ−sY(2:2) is sth inverse moment of larger observation in a sample of size 2 from G2(y).
4.2. Conditional moments
The conditional moments are useful in studying the properties of the conditional distributions. In case of two random variables, we can obtain the conditional moments of X given Y = y and conditional moments of Y given X = x. These moments are defined as
Now, using the conditional distribution of X given Y = y, the rth conditional moment of X given Y = y is
which on simplification becomes
Similarly, the sth conditional moment of Y given X = x can be obtained by using the conditional distribution of Y given X = x in
and is given as
The conditional means and conditional variances can be easily obtained from (14) and (15).
4.3. Bivariate reliability and hazard rate functions
The bivariate reliability and hazard rate functions play important role in reliability analysis, see for example [24] and [25]. The bivariate reliability function is defined as
Now, using the joint and marginal cdf's for the proposed bivariate family of distributions, the bivariate reliability function is given as
where S1(x)=1−G1(x), S2(y)=1−G2(y), b=λ1+λ3 and d=λ2+λ3. The bivariate reliability function can be computed for different baseline distributions and different values of the parameters.
The bivariate hazard rate function is defined as, see [26],
The bivariate hazard rate function for the proposed bivariate family of distributions can be obtained by using (8) and (16) in above equation and is given as
where b and d are defined earlier.
4.4. The dependence measures
The dependence measures are useful to see the strength of dependence between two random variables. Different dependence measures can be computed for a joint probability density function, see for example [11,12,27]. In the following we will discuss some important dependence measures for the new bivariate family of distributions.
4.4.1. Kendall's Tau coefficient
The Kendall's Tau coefficient is a useful measure to see the dependence between two continuous random variables. The coefficient is defined as
Using the joint density and distribution functions of the new bivariate family of distributions, we have
Making the transformation u1=G1(x) and u2=G2(y), we have
Solving the above double integral, the Kendall's Tau coefficient for the new bivariate family of distributions is given as
The Kendall's Tau coefficient does not depend upon the underlying base distribution.
4.4.2. Spearman's Rho coefficient
The Spearman's Rho coefficient is another useful dependence measure to see the dependence between two random variables. The coefficient is defined as
Using the joint and marginal cdf's and the marginal density functions of X and Y for the new bivariate family of distributions, we have
Making the transformation u1=G1(x), u2=G2(y) and solving the resulting integral, we have
We can see that the Spearman's Rho will always be smaller than the Kendall's Tau for the new bivariate family of distributions.
4.4.3. The local dependence measure
The local dependence measure for a bivariate family of distributions is defined by [27] as
which for the new bivariate family of distributions is
where λ=λ1+λ2+λ3. We can see that the local dependence measure depends upon the baseline distribution.
4.5. Random sample generation
The random sample from the proposed bivariate family of distributions can be generated by using the conditional distribution approach. In this approach the random variate from a bivariate distribution is obtained by using the following steps:
1) Generate a random observation from the marginal distribution of X, FX(x), and call it x.
2) Generate a random observation from the conditional distribution of Y given X = x, FY|x(y|x), and call it y.
3) The pair (x,y) is a random observation from the joint distribution FX,Y(x,y).
Now, to use this method for the proposed bivariate family of distributions we have following steps:
a) We first generate a random observation from the marginal distribution of X by solving
for x where u1 is a uniform random number. Solving above equation for x, a random observation from the marginal distribution of X is
where u∗1=12b{(1+b)±√(1+b)2−4bu1} and choice between larger or smaller root is done to have an admissible solution.
b) To apply the second stem, we first obtain the conditional cdf of Y given X = x as
Now, the random observation from the conditional distribution of Y given X = x can be obtained by solving
for y where u2 is another uniform random observation. The solution of above equation for y is
where u∗2=12λ2(x){λ1(x)±√λ21(x)−4u2Δ2(x)λ2(x)}, λ1(x)=1+λ−2λ1G1(x) and λ2(x)=λ2+2λ3G1(x).
c) The pair (x,y) given in (21) and (22) is a random observation from the new bivariate family of distributions.
d) Repeat steps 1–3 n times to obtain a random sample of size n from FX,Y(x,y) given in (7).
4.6. Stress-strength reliability analysis
A stress-strength reliability analysis is very useful in engineering and survival analysis, see for example [28]. The reliability of the stress-strength model is computed as R=P(Y<X) where Y is stress and X is strength. Now, if the stress (Y) and strength (X) are dependent and have joint bivariate distribution given in (8) then the reliability is given as
assuming that both X and Y are positive random variables. Simplifying above integral, the stress-strength reliability of two components X and Y having joint distribution given in (8) is
Further, if X and Y have identical distributions, that is if G1(x)=G2(x)=G(x) then the reliability is
which on simplification becomes
We can see that the reliability in case of identical distributions of X and Y does not depend upon the baseline distribution.
4.7. Parameters estimation
In this section we will discuss the maximum likelihood estimation of the parameters for the new bivariate family of distributions under the assumption that all the parameters of baseline distributions G1(x) and G2(y) are known. For this, suppose X1,X2,…,Xn is a random sample of size n from the bivariate transmuted family of distributions. The likelihood function is
where λ=λ1+λ2+λ3. The log-likelihood function is
The derivatives of log-likelihood function with respect to λ1, λ2 and λ3 are
and
The maximum likelihood estimators of λ1, λ2 and λ3 are obtained by equating (26)–(28) to zero and numerically solving the resulting equations.
In the following section we will give a multivariate extension of the bivariate family of distributions discussed above.
5.
A new multivariate family of distributions
A multivariate extension of the bivariate T-X family of distributions, given in (5), is
where x=(X1,X2,…,Xp) is a vector of p random variables and r(v1,…,vp) is any multivariate distribution with support on [a1,b1]×⋯×[ap,bp]. A simpler version of above family has the following form when domain of r(v1,…,vp) is on [0,1]p
The multivariate T-X family of distributions, given in (29), can be used to obtain new multivariate families of distributions for suitable choices of r(v1,…,vp). We have proposed a new multivariate family of distributions by using
in (29). The joint cdf of the new multivariate family of distribution is
which on simplification becomes
where Gi(xi) is marginal cdf of ith random variable Xi and (λ1,λ2,…,λp+1) are the parameters such that ∑p+1i=1λi≥−1, ∑pi=1λi+(p+1)λp+1≤1, λi∈[−1,1] and −1≤λi+λp+1≤1 for i=1,2,…,p. The joint density function of the new multivariate family of distributions is
where gi(x) is the density function corresponding to Gi(xi) and λ=∑p+1i=1λi. It can be easily seen that the marginal density function of any random variable, Xi, for the joint density (31) is same as given in (1) with parameter λi+λp+1. We can also see that the joint marginal distribution for any pair of random variables, (Xi,Xm), for the joint density (31) is the same as given in (8).
The marginal density function of a subset of random variables x1=(X1,X2,…,Xt) for the new multivariate family of distributions is readily written from (31) as
The conditional density function of any random variable Xi given the information of all other random variables is easily obtained by using
where x(i) is the random vector x without Xi. The conditional distribution of Xi given the information of all other variables for the proposed multivariate family of distributions is
where Δi(x(i))=[1+∑ph≠i=1λh{1−2Gh(xh)}+λp+1{1−2p−1∏ph≠i=1Gh(xh)}].
The joint conditional distribution of any pair of random variables (Xi,Xm) given the information of all other variables is obtained by using
where x(i,m) is the random vector x without Xi and Xm. The joint conditional distribution of (Xi,Xm) given the information of all other variables for the proposed multivariate family of distributions is
for (xi,xm)∈R2 where
In general, the conditional distribution of one subset of variables x1 given the information of other subset of variables x2 for the new multivariate family of distributions is
where Δ2(x2)=[1+∑ph=t+1λh{1−2Gh(xh)}+λp+1{1−2p−t∏ph=t+1Gh(xh)}].
Some properties of the new multivariate family of distributions are given in the following.
5.1. Marginal, joint and conditional moments
The marginal and joint moments for the proposed multivariate family of distributions can be easily obtained in the same way as discussed above in the case of the new bivariate family of distributions. The conditional moments of a single random variable given the information of all other variables can be obtained by using
Now, using the conditional distribution of xi given the information of all other variables from (33), we have
or
The joint conditional moments of (Xi,Xm) given the information of other random variables can be obtained by using
Now, using the joint conditional distribution from (34), we have
Simplifying above integral, the joint conditional moment of (Xi,Xm) given the information of other random variables is
The conditional means, variances and conditional covariances can be obtained from (36) and (37).
5.2. The multivariate dependence measures
In the following we have given the multivariate dependence measures for the proposed multivariate family of distributions. We have discussed two multivariate dependence measures which are the Kendall's Tau and Spearman's Rho. These measures are given in the following.
5.2.1. Kendall's Tau coefficient
The multivariate extension of Kendall's Tau coefficient is given as see [29],
Now, using the joint distribution and density functions of the proposed multivariate family of distributions, from (30) and (31), we have
Making the transformation Gi(xi)=ui, we have
Solving above multiple integrals, the Kendall's Tau coefficient for the proposed multivariate family of distributions is
We can see that for p = 2 the expression (38) reduces to (18) as it should be.
5.2.2. Spearman's Rho coefficient
The multivariate extension of Spearman's Rho coefficient is given as see [30],
Now, using the joint distribution function and marginal density functions of individual variables we have
Making the transformation ui=Gi(xi), we have
Simplifying above multiple integral, the Spearman's Rho for the proposed multivariate family of distributions is
It can be easily seen that (39) reduces to (19) for p = 2 as it should be.
5.3. Parameters estimation
In the following we have given maximum likelihood estimator for parameters of the proposed multivariate family of distributions when all the parameters of the base distribution are known. For this, we assume that a random sample of n vector observations is available from the joint density function (31). The likelihood function is
where λ=(λ1,λ2,…,λp+1) is vector of unknown parameters. The log of likelihood function is
The derivatives of log of likelihood function for λi;i=1,2,…,p and λp+1 are
and
The maximum likelihood estimators can be obtained by numerically solving above (p+1) equations.
We will now study a special case of the proposed bivariate and multivariate families of distributions for Weibull baseline distribution.
6.
New bivariate and multivariate Weibull distributions
In this section we have discussed new bivariate and multivariate Weibull distributions by using Weibull baseline distribution, proposed by [31], in the new bivariate and multivariate families of distributions proposed above.
6.1. A new bivariate Weibull distribution
In the following we have given a new bivariate Weibull distribution by using following baseline Weibull distributions for X and Y in (7) and (8)
The joint distribution function of the new bivariate Weibull distribution is
where (x,y,α1,α2,θ1,θ2)>0. Also (λ1,λ2,λ3)∈[−1,1], λ1+λ2+λ3≥−1, λ1+λ2+3λ3≤1, −1≤λ1+λ3≤1 and −1≤λ2+λ3≤1. The density function corresponding to (42) is
or
where ΔBW(x,y)=[1−λ+2λ13e−(xθ1)α1+2λ23e−(yθ2)α2−2λ3{1+2e−(xθ1)α1−(yθ2)α2}], λ13=(λ1+2λ3) and λ23=(λ2+2λ3). The marginal distributions of X and Y are immediately written from (43) as
and
The conditional distributions of X given Y = y and of Y given X = x are readily obtained from (9) and (10) and are
and
where ΔBW(x)=1+b−2be−(xθ1)α1 and ΔBW(y)=1+d−2de−(yθ2)α2. The conditional distributions are useful in studying the conditional behavior of one random variable given the information of other.
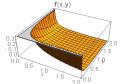
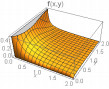
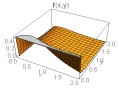
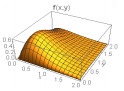
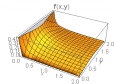
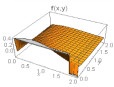
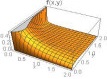
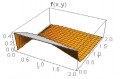
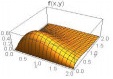
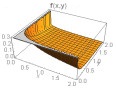
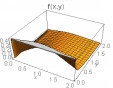
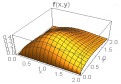
Some plots of the joint density function are given in Table 1 below for θ1=θ2=1 and for different combinations of other parameters.
From above graph we can see that the shape is controlled by parameters α1 and α2. The joint hazard rate function of the distribution is immediately written from (17) as
where Δ∗BW(x,y)=[1−λ+λ13e−(xθ1)α1+λ23e−(yθ2)α2−λ3{2+e−(xθ1)α1−(yθ2)α2}]. The hazard rate function can be plotted for different combinations of the parameters.
Some important properties of the proposed bivariate Weibull distribution are in the following.
6.1.1. The joint and conditional moments
We have seen that expressions for joint, marginal and conditional moments of the new bivariate family of distributions involve moments of baseline distribution and moments of larger observation in a sample of size 2 from the baseline distribution. It is known that the rth moment and rth moment of larger observation in a sample of size 2 from Weibull distribution with density
are given as
Using these expressions in (11) the joint moments for the new bivariate Weibull distribution is
Again, using simple moments and moments of order statistics of Weibull distribution in (14) and (15), the conditional moments for the new Weibull distribution are
and
The conditional means and conditional variances can be obtained from (48) and (49).
6.1.2. The dependence measures
We have discussed different dependence measures in Section 4.4. We have seen that two of the dependence measures, namely Kendall's Tau and Spearman's Rho do not depend upon a specific baseline distribution. We have also seen that the local dependence measure, given (20), depends upon a specific distribution. The local dependence measure for the new bivariate Weibull distribution can be obtained by using the density and distribution functions of Weibull random variables in (20) and is
The local dependence measure can be computed for specific values of the parameters. We can see that γ(x,y) is positive if (λ1+λ3)(λ2+λ3)<−λ3 and is negative otherwise.
6.1.3. Stress-strength reliability
In the following we have obtained the stress-strength reliability if the stress (Y) and strength (X) have joint bivariate distribution given in (43). We have seen that the stress-strength reliability of for the new bivariate family of distributions is given in (23) as
Now, using G1(x)=1−e−(xθ1)α1 and G2(x)=1−e−(xθ2)α2, the reliability for the new bivariate Weibull distribution is
or
Simplifying the above integral, the reliability coefficient for the new bivariate Weibull distribution is
The reliability coefficient can be computed for specific values of the parameters.
6.1.4. Random Sample Generation
A random sample from the proposed bivariate Weibull distribution can be obtained by using the algorithm given in Section 4.5. An algorithm to generate a random sample from the proposed bivariate Weibull distribution is listed below.
1) Generate a random observation from the marginal distribution of X by using
where u∗1=12b{(1+b)±√(1+b)2−4bu1} and choice between larger or smaller root is done to have an admissible solution.
2) Generate a random observation from the conditional distribution of Y given X = x by using
where u∗2=12λ2(x){λ1(x)±√λ21(x)−4u2Δ2(x)λ2(x)}, λ1(x)=1+λ−2λ1{1−e−(xθ1)α1}, λ=λ1+λ2+λ3 and λ2(x)=λ2+2λ3{1−e−(xθ1)α1}.
3) The pair (x, y) in (52) and (53) is a random observation from the proposed bivariate Weibull distribution.
6.1.5. Parameter estimation
In the following we will discuss maximum likelihood estimation for parameters of the new bivariate Weibull distribution. For this suppose that a random sample of n observations is available from the joint density given in (43). The likelihood function is
where θ=(α1,α2,θ1,θ2,λ1,λ2,λ3) and
The log of likelihood function is
The derivatives of log-likelihood function with respect to the unknown parameters are
and
The maximum likelihood estimator of parameter vector θ=(α1,α2,θ1,θ2,λ1,λ2,λ3) can be obtained by numerically solving (55)–(61).
We will, now, briefly discuss a new multivariate Weibull distribution by using the proposed multivariate family of distribution.
6.2. A new multivariate Weibull distribution
In the following we have given a new multivariate Weibull distribution by using following baseline Weibull distributions for Xi in (30) and (31)
The joint distribution function of the new multivariate Weibull distribution is
The density function corresponding to (60) is
The marginal and conditional distributions can be easily obtained by using the methods given in Section 5. In particular the joint marginal distribution of any pair of random variables is same as given in (43). Further, the conditional distribution of any random variable given the information of other random variables can be obtained by using (33). In particular, the joint conditional distribution of any two random variables given the information of all other variables can be obtained by using (34) and is
where
and
The joint conditional moments for any two random variables given the information of all other variables can be obtained by using (37). Now, using the raw moments of a Weibull random variable and moments of maximum in a sample of size 2 from the Weibull distribution, the joint conditional moments between Xi and Xm given the information of other random variables for the proposed multivariate Weibull distribution is
where Δ∗i,m(x(i,m))=1+λ−2∑ph≠i,m=1λh{1−e−(xhθh)αh}.
The conditional means, conditional variances and conditional covariances can be obtained from (65). We will now give some numerical study about the proposed bivariate Weibull distribution.
7.
Numerical study
In this section we have given some numerical study for the proposed bivariate Weibull distribution. The study contains simulation study and real data application. These are given in the following subsections.
7.1. Simulation study
In this section we will give a simulation study for the proposed bivariate Weibull distribution. The simulation algorithm is given below.
1) Generate a random sample of specific size n, by using different values of the parameters, from the bivariate Weibull distribution by using the steps given in Sub-section 6.1.4.
2) Compute maximum likelihood estimates of the parameters by using the sample obtained in Step 1.
3) Repeat Steps 1 and 2 for a specific number of times, say M.
4) Obtain the simulated estimate and simulated mean square error of the estimate by using
where ˆθk is kth parameter and ˆθkj is kth parameter obtained from jth sample.
We have conducted simulation study by using samples of sizes 20, 50,100,200 and 500 and the number of simulations used are 20000. The results are given in Table 2 below.
From results of above table, we can see that the estimated values are close to pre-specified values of the parameters and hence the maximum likelihood estimates are consistent. We can also see that the mean square error (in parenthesis) of the estimates decreases with increase in the sample size.
We will now give a real data application to compare the proposed bivariate Weibull distribution with some available bivariate distributions.
7.2. Real data application
In the following a real data application will be given where the proposed bivariate Weibull distribution is compared with some available bivariate distributions. We have used two data sets for comparison of the proposed bivariate distribution with some existing bivariate distributions. The first data set that we have used is the mammal brain data (Data 1) that has been obtained from [32]. This data set contains body weight of mammals (X) and the brain weigh (Y) of 84 mammals. The second data set that we have used is the child smoker data (Data 2) that has been obtained from [34]. This data set contains information about forced expiratory volume (X) and height (Y) of 655 children. Some summary measures of the data are given in Table 3 below.
The summary measures indicates that both of the variables in data 1 are positively skewed whereas for second data one variable is positively skewed and one is negatively skewed. We have fitted the proposed bivariate Weibull distribution on this data alongside three more bivariate distributions. The other distributions fitted on the data are a bivariate exponential distribution by [33], a bivariate Weibull distribution by [34] and a bivariate Weibull distribution obtained by using the Gumbel copula. The joint density functions of these bivariate distributions are Bivariate Exponential [33]
Bivariate Weibull [34]
Bivariate Weibull with Gumbel copula
where x>0,y>0,α1>0,α2>0,β1>0,β2>0 and −1≤γ≤1.
The distributions are fitted by computing the maximum likelihood estimates of the parameters of various distributions. The maximum likelihood estimation has been done by using "maxLik" package of R, [35]. The maximum likelihood estimates alongside the standard errors are given in the Table 4 below.
We have next computed some goodness of fit measures to decide about the most suitable model for the data. These summary measures are given in Table 5 below.
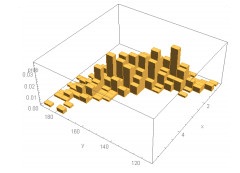
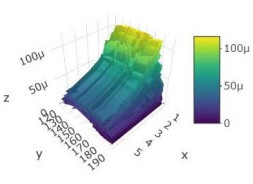
From Table 5, we can see that the proposed bivariate Weibull distribution is the best fit for both of the data sets as it has smallest value of AIC and BIC. We have also plotted the bivariate histograms of two data sets alongside the fitted distribution and are given in Table 6, below.
From above figures in Table 6 we can see that the fitted distributions are reasonable fit to the two data sets.
8.
Conclusions
In this paper we have proposed new bivariate and multivariate families of distributions. These families of distributions are useful to generate the new bivariate and multivariate distributions from the univariate marginals. We have studied some important properties of the proposed families of distributions. We have seen that the moments of the proposed families of distributions depend upon the raw moments and moments of order statistics for the baseline distributions. The measures of dependence of the proposed families have also been discussed. We have also given the stress-strength reliability analysis for the proposed bivariate family of distributions. We have studied the proposed bivariate and multivariate families of distributions for the baseline Weibull distribution and have proposed new bivariate and multivariate Weibull distributions. We have studied some useful properties of the proposed bivariate Weibull distribution including moments, reliability and maximum likelihood estimation of the parameters. The simulation study and real data application of the proposed bivariate Weibull distribution has been done by using the mammal brain data. We have seen that the proposed bivariate Weibull distribution is the best fit for the data used. The proposed bivariate and multivariate families of distributions can be explored for different baseline distributions.
Conflict of interest
The authors declare that they have no conflicts of interest.













 DownLoad:
DownLoad: