Shock stability of a novel flux splitting scheme

1.   Introduction

The nature of the supersonic flows, especially internal flow, is highly complex compressible viscous flow, which contains many complex flow field structures including strong shock waves, shear waves, shock-shock interactions, shock-boundary interactions, and vortices ^[1,2]. The accurate simulation of these complex flow field structures requires numerical methods, which have low numerical dissipation, small numerical oscillation, good stability, and high resolution at cell interfaces ^[3,4].

There have been some theoretical advancements on the shock stability in the past 20 years, for example, Shen ^[5] studied shock solutions of the compound Burgers-KdV equation using the qualitative theory of differential equations and the ansatz method. Blake Barker et al. ^[6] considered some basic questions regarding the relations between inviscid and viscous stability and the existence of a convex entropy through a combination of analytical and numerical techniques. Based on the theory of algebraic curves, Xue ^[7,8] analyzed the quasi-periodic solutions of coupled KdV-type equations and Jaulent-Miodek equations with a negative flow.

In addition, many scholars have given a large number of related algorithm schemes to capture the shock stably. Generally, these algorithms may be classified as below, such as two-step predictor-corrector approach ^[9], convex flux ^[10], upwind method ^{[11,12,13,14,15,16,17,18,19]}, modified SLAU2 scheme bifurcation ^[20], and sharp interface method ^[21]. In this article, the main research focuses on the upwind method.

The upwind method is considered to be the most efficient numerical tool to simulate supersonic flow problems, and it can be classified into two groups: flux difference splitting schemes (FDS) ^[12,13] and flux vector splitting schemes (FVS) ^[14,15,16]. The FDS method has low dissipation and it can accurately capture the contact discontinuity, which represents a linear wave, since the contact discontinuity is the limiting case of the boundary layer, so the FDS method is suitable to simulate the boundary layer. When capturing the nonlinear shock, the performance of the FDS method is also very prominent. However, when simulating the slowly-moving shock wave, the FDS method produces low frequency post shock fluctuations and the 'carbuncle' phenomenon occurs when simulating a strong shock. Most of the low dissipation methods are faced with the same problems ^[22,23]. The FVS method can accurately capture the shock front, and its computational efficiency and robustness are generally better than the FDS method. However, classical FVS methods, such as the van-Leer method and Steger-Warming method, cannot effectively simulate contact discontinuity and shear layers ^[17]. The strong dissipation limits the application of this method in boundary layer flow problems. Therefore, the development of the upwind method, which is low dissipative and robust, is the key to simulating supersonic flow problems.

In recent years, scholars represented by Liou and Zha considered the different propagation mechanisms between the convective item information and pressure item information, and they developed a class of convective upwind splitting schemes. This class method combined the low dissipation property of the FDS method and the robustness of the FVS method. They can accurately capture linear and nonlinear waves, which are suitable to simulate the boundary layer, and they showed good stability when capturing a strong shock. Liou's advection upstream splitting method (AUSM) ^[24,25] decomposes the flux vector into the convective and pressure parts, with the convective quantity in the energy equation represented by the total enthalpy $H$. Zha's splitting scheme ^[3] is similar to Liou's, except that the convective quantity in the energy equation is the total energy $E$. Recently, Toro ^[17] proposed a new flux splitting scheme (TV method, named after the authors), which also decomposes the flux vector into the convective and pressure parts. However, unlike Liou's and Zha's schemes, they use the kinetic energy $K$ as the convective quantity in the energy equation. According to the analysis in the literature ^[17], the convective part of this splitting scheme does not contain the pressure variable, and the information related to pressure is contained in the pressure part. In contrast, Liou's and Zha's schemes do not satisfy this property. Based on the different propagation mechanisms between the convective information and pressure information, we consider that Toro's splitting scheme is more reasonable. Sun et al. ^[26] proposed a flux splitting method for all-speed flows with low dissipation based on Toro's splitting method. Through the numerical experiments, we can get the conclusion that although the TV method meets the low dissipation, its shock stability is poor in capturing the strong shock and 'carbuncle' phenomena that occurs. Based on Toro's splitting flux scheme and learned from the construction thought of Mandal's HLL-CPS ^[18], a new flux splitting scheme HLL-CPS-T (where T represents Toro, as HLL-CPS-Z and HLL-CPS-L ^[18]) was proposed in this paper, and its shock stability and dissipation at the contact discontinuity are analyzed.

Several attempts have been done to cure numerical shock instabilities in the past few years. Fleischmann et al. ^[27] proposed a new possible mechanism of the grid-aligned shock instability. A wrong scaling behavior of numerical dissipation due to the local low Mach number in transverse direction of the shock front propagation was found to cause the numerical shock instability. Moreover, Fleischmann et al. ^[28] demonstrated that the grid-aligned shock instability can strongly affect simulation results when the grid resolution is increased. Beyond the well-documented two-dimensional behavior, the problem is particularly troublesome with three-dimensional simulations. Hence, there is a need for shock-stable modifications of HLLC-type solvers for high-speed flow simulations. Kemm ^[29] suggested to decrease viscosity on acoustic waves for low Mach numbers to prevent the 'carbuncle' phenomenon in gas dynamics simulations.

There are some different explanations for the causes of the 'carbuncle' phenomenon: Liou ^[30] analyzed the mass flux of various upwind methods and concluded that the pressure coefficient of the mass flux dissipation term not being zero causes the 'carbuncle' phenomenon; Xu and Li ^[31] believed that the low dissipation property in the direction tangential to the shock front induces the 'carbuncle' phenomenon; Sun and Takayama ^[32] pointed out that an amount of dissipation is introduced in the shear wave and, when the diffusion on tangential velocity is suppressed, 'carbuncle' phenomena appear. In their study, Pandolfi and D'Ambrosio ^[23] identified the interaction between pressure and density perturbations in a method as a key factor in the occurrence of the 'carbuncle' phenomenon. Based on Pandolfi and D'Ambrosios' work ^[23], through the analysis of TV and HLL-CPS-T schemes' physical quantities' disturbance attenuation properties in Quirk's odd-even decoupling problem, we try to give the numerical shock stability condition for upwind methods, but the conclusion is different from Pandolfi and D'Ambrosios'. The decay characteristics of shock normal velocity perturbations are the key factor determining whether a scheme exhibits the 'carbuncle' phenomenon, as we have found in our study. This conclusion can be utilized to analyze the shock stability of existing upwind methods and serve as a foundation for the development of new types of shock-capturing methods.

The paper is organized as follows. First, in Section 2, we give the construction of the new splitting scheme. We present in Section 3 the numerical dissipation analysis of the splitting schemes. Section 4 of the paper provides a detailed analysis of shock stability, along with an inference and its verification. Section 5 presents the numerical results for various carefully selected test problems. Detailed theoretical comparison with the method of Sun et al. ^[26] is given in Section 6. The paper concludes with a summary of the findings in Section 7.

2.   The governing equation and the new flux splitting scheme

2.1.   Euler equations

The paper focuses exclusively on the Euler equations. Specifically, the two-dimensional Euler equations in conservation-law form are presented as

where U, F(U), and G(U) are the vectors of conserved variables and fluxes, given respectively by

Here, $\rho$ is density, $u$ and $v$ are particle velocity vector components, $p$ is pressure, and $E$ is the total energy, satisfying the equation of state

where $\gamma = 1.4.$ A numerical method for solving Eq (2.1) is

where ${{{\bf{F}}_{i + 1/2}}}$ and ${{{\bf{G}}_{j + 1/2}}}$ are the numerical fluxes at the interface.

2.2.   HLL-CPS-T method

The flux vector ${\bf{F}}\left({\bf{U}} \right)$ was split into convective part ${\bf{C}}\left({\bf{U}} \right)$ and pressure part ${\bf{P}}\left({\bf{U}} \right)$ according to Toro's flux splitting scheme ^[17], that is,

where,

The normal velocity is defined as:

According to E. F. Toro ^[14] and the one-dimensional Euler equations in the conservation-law form (2.1) and (2.2), the Jacobian matrix $A$ is given by

The partial differential equation system exhibits hyperbolicity with real eigenvalues

The matrix $K$ of corresponding right eigenvectors is

So, the associated wave speeds corresponding to the above convective flux component ${\bf{C}}\left({\bf{U}} \right)$ are $({u_n}, {u_n}, {u_n}, {u_n})$, and those of the pressure flux component ${\bf{P}}\left({\bf{U}} \right)$ are considered as $(- a, 0, 0, a)$. In this way, the advection term contains no pressure terms and all the pressure terms are included in the pressure flux ^[17].

In what follows, similar to Sun's approach ^[26], we will handle the convective and pressure fluxes separately. However, our main interest lies in conducting numerical dissipation and shock stability analysis for the scheme constructed when $f(M) = 1$. (In ^[26], $f(M) = \min \{ {M_{local}}, 1\}$ appears in the dissipation term Eq (20), where $M$ is the Mach number. For the sake of research, we will only consider $f(M) = 1$ here). Through the detailed analysis of the TV and HLL-CPS-T schemes' physical quantities' disturbance attenuation properties, we aim to derive numerical conditions for upwind methods to ensure shock stability, thereby avoiding the occurrence of the 'carbuncle' phenomenon during shock capturing. Convective flux is processed by the upwind mode. The propagation direction of convective information depends on the Mach number at the interface as showed in ^[18]. That is,

where $\bar u_n = \frac{{{{u_{nL}}} + {{u_{nR}}}}}{2}$ and the definitions of the Mach number at the interface and the sound speed are

${S_L}{\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {S_R}$ denote the fastest speed of the left and right traveling waves

where $\tilde u_n$ and $\tilde a$ are the average velocity and average sound speed calculated by Roe's method. To ensure fully one-sided flux in the supersonic regime, a zero has been included in the above expressions (2.8).

The calculation of pressure flux is based on the HLL-type Riemann solver. The extreme propagation speed ${S_L}{\kern 1pt} {\kern 1pt}$ and ${\kern 1pt} {S_R}$ of the entire system is chosen instead of the propagation speed of the pressure part of the system. This is because the resulting HLL flux scheme is a stable scheme, which guarantees the positive nature of the dissipation matrix. This flux function is 'carbuncle' free, so the capture of the shock wave is stable. What is more, we use the replacement of density by pressure divided by speed of sound squared in the term ${S_L}{\rm{ - }}{S_R}$ in the HLL flux scheme; this is because although the HLL flux scheme ensures zero dissipation for a contact discontinuity, its shock stability is poor in capturing the strong shock wave and 'carbuncle' phenomena occur.

Now, assume that the flow satisfies the isentropic condition ${\bar a^2} = \Delta p/\Delta \rho$ ^[32], and we have

The interface numerical flux ${{\bf{F}}_{1/2}}$ is made out from two contributions, that is,

3.   Numerical dissipation analysis

The capability to identify contact discontinuities and intermediate characteristic fields is a crucial criterion for evaluating the effectiveness of a method in simulating boundary layer flow problems. A stationary contact discontinuity is a particular instance of an intermediate field ^[17], which is frequently employed as a benchmark problem for testing numerical methods. To analyze the dissipation of the numerical scheme at the contact discontinuity in the one-dimensional equations, the flux vector can be written in dissipation form:

where ${{\bf{D}}_{1/2}}$ is the dissipation term. According to the splitting scheme HLL-CPS-T proposed by this paper, ${{\bf{D}}_{1/2}}$ 's components are

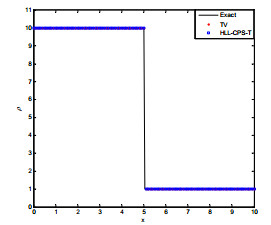
At the contact discontinuity ${(u, \; p)_L} = {(u, \; p)_R} = ({u_c}, \; p), \; {\rho _L} \ne {\rho _R}$, we conduct the dissipation term ${{\bf{D}}_{1/2}}{|_{1, 2, 3}} = 0$, so the HLL-CPS-T scheme can capture the stationary contract discontinuity exactly.

The results obtained by TV and HLL-CPS-T schemes in solving the stationary contract discontinuity are depicted in Figure 1, where $({\rho _L}, {u_L}, {p_L}) = (1, 0, 1)$, $({\rho _R}, {u_R}, {p_R}) = (10, 0, 1)$. Figure 1 clearly demonstrates that the results produced by the HLL-CPS-T scheme are consistent with the exact solution and show no dissipation at the discontinuity. Therefore, this scheme is suitable for simulating boundary layer flow problems.

4.   The analysis of shock stability

4.1.   The linear analysis of Quirk's odd-even problem

Quirk's odd-even decoupling problem is a powerful numerical example in analyzing the occurrence mechanism of the 'carbuncle' phenomenon ^[33]. The problem involves the travel of a set of shock waves that commence their propagation from the left side of the duct, moving rightward, and an artificial perturbation $\Delta y = \pm 1{0^{ - 3}}$ was added to the vertical side of the mesh centerline, just as in Figure 2.

Figure 3 shows the numerical results of the TV and HLL-CPS-T flux splitting schemes in solving Quirk's odd-even decoupling problem. We can see that the results of the TV scheme appear as shock-unstable and the shock front is distorted after the shock propagating through some distance in the tube, while the results of the HLL-CPS-T scheme can capture the shock well and it appears shock-stable. For a variety of upwind methods, Pandolfi and D'Ambrosio have analyzed the perturbation attenuation of physical quantity $(\hat \rho, \hat u, \hat p)$ by using the linear analysis method ^[23]. In this paper, this method is used to analyze the TV and HLL-CPS-T schemes, trying to get a numerical shock stability condition for the upwind methods.

For analysis, we make the assumption that the computational grid is evenly distributed, with mesh spacing $\Delta y$ and normalized values as follows:

and that the discrete solution at a time ${t^n}$ is given by:

if $j$ is odd:

if $j$ is even:

Here, ${\hat \rho ^n}$, ${\hat u^n}$, and ${\hat p^n}$ are the density, velocity, and pressure perturbation, respectively. We have assumed the initial perturbation of the velocity component along $y$ to be null, i.e., ${\hat v^0} = 0$ (this assumption here is based on reference ^[23]. In the first paragraph of Section 5, they give initial value ${v_0} = 0$, and in the cells $v = {v_0} + \hat v = 0$, i.e., $\hat v = 0$. This means that they have the assumption ${\hat v^0} = 0$.).

Numerical flux at the interface is ${{\bf{F}}_{i + 1/2}} = {\left({\kern 1pt} {\kern 1pt} {\rho v, \rho uv, p + \rho {v^2}, v\left({p + E} \right)} \right)^{\rm T}}$. The physical quantities' disturbance expressions of the TV and HLL-CPS-T flux splitting schemes can be obtained by solving Eq (2.3), and they are reported in Table 1. It should be noted that, in this particular problem, the variable represents the velocity component normal to the interface rather than the tangential component. The time step of the integration ($\Delta t$) appears in the Courant number $\upsilon = \sqrt \gamma {\Delta t}/{\Delta y}$, where $\gamma$ is the ratio of the specific heats and is equal to 1.4 for air. Moreover, the CFL (Courant-Friedrichs-Levy) number appears in Section 5 as ${{c\Delta t} / {\Delta x}}$, which meets the CFL condition

where $c = \mathop {\max }\limits_{k, x \in R} \left| {{\lambda _k}\left({U\left({x, 0} \right)} \right)} \right|$ ^[34].

Figures 4–7 show the perturbation attenuation curves of the TV scheme with the different amounts of initial perturbation, which are drawn according to the iteration formulas in Table 1. Case 1: As Figure 4, in the case of the initial perturbation ${\hat p^0} = {\hat u^0} = 0$ and the initial density perturbation ${\hat \rho ^0} = 0.01 \ne 0$, the density perturbation holds the initial value and remains unaltered with time step as $k \to \infty$. Perturbation neither converges nor amplifies and the pressure perturbation and the velocity perturbation remain zero. Case 2: As Figure 5, the physical perturbation attenuation curve is given with the circumstance of the initial perturbation ${\hat \rho ^0} = {\hat u^0} = 0$ and the initial pressure perturbation ${\hat p^0} = 0.01 \ne 0$. As can be seen, the density perturbation decreases to a finite value ${\hat \rho ^\infty } = - {\hat p^0}/\gamma$ with the effect of pressure perturbation, then remains constant. Pressure perturbation rapidly decays to zero, but the velocity perturbation holds the initial value of zero unchanged. Case 3: As in Figure 6, in this case, the initial perturbations ${\hat p^0} = {\hat \rho ^0} = 0$ and the initial velocity perturbation ${\hat u^0} = 0.01 \ne 0$, the density perturbation and the pressure disturbance keep the initial value zero, and the velocity perturbation holds the initial value, which does not decay with the increasing of a time step $k$. To the HLL-CPS-T scheme, it is the same as the TV scheme for cases 1 and 2, but the difference is that in case 3 (as Figure 7), the density perturbation and pressure perturbation remain at the initial value zero, the velocity perturbation decays quickly to zero, then remains unchanged, so its velocity perturbation is damped.

Pandolfi ^[23] identified that the occurrence of the 'carbuncle' phenomenon, which can distort the accuracy of shock-capturing methods in computational fluid dynamics, depends on how pressure perturbations interact with density perturbations. This was observed during their analysis of the Roe scheme's shock stability. By conducting calculations, we obtain that Roe and TV schemes have the same physical disturbance expressions, so we can see that the interaction of HLL-CPS-T and Roe schemes' pressure perturbations and density perturbations are the same form in Figures 4 and 5 and the pressure perturbations and density perturbations attenuation properties of the two methods are the same. The only difference is the velocity perturbations attenuation properties between the two methods, so it is the key factor in determining the occurrence of the 'carbuncle' phenomenon. We conduct the inference: A sufficient condition to ensure shock stability for an upwind method is found to be that velocity perturbation is damped and ${\hat u^\infty }$ is zero as the time step $k \to \infty$.The theoretical analysis is given in Section 4.2.

4.2.   The occurrence mechanism of the 'carbuncle' phenomenon

In this section, we attempt to give the possible reasons for the 'carbuncle' phenomenon for low dissipation schemes and show the theoretical analysis of the velocity perturbation attenuation properties as the key factor in determining the occurrence of the 'carbuncle' phenomenon. Xu and Li divided the shock layer into subsonic and supersonic regions when they analyzed the stationary shock ^[31]. The fluid trajectory was considered as moving in the quasi-one-dimensional nozzles (just as in Figure 8).

According to the relationship of gas dynamics, it can be seen that

Xu and Li suggest that the occurrence of the 'carbuncle' phenomenon in upwind schemes is due to the fact that in the subsonic region, an increase in velocity $\left({du > 0} \right)$ is inevitably accompanied by a decrease in pressure $\left({dp < 0} \right)$, which creates a localized low-pressure area. Low-dissipation schemes lack sufficient numerical viscosity in the direction parallel to the shock wave to weaken the velocity gradient. Consequently, the surrounding fluid flows toward the low-pressure area under the driving force of the pressure gradient, leading to a continued increase in local velocity and a subsequent decrease in pressure; by this way, the unstable phenomenon is appeared.

Assumed that along the flow direction, the changes of local velocity and pressure we get from velocity perturbation and pressure perturbation, respectively, we obtain $du = {\hat u^k}, dp = {\hat p^k}$. Combined with the linear analysis method in Section 4.1, the relationship between local velocity perturbation and pressure perturbation can be found by using Eqs (4.1) and (4.2). We get

and the relationship of velocity perturbation damping goes as

where $\alpha$ denotes the damping coefficient. When $0 < \alpha < 1$, the velocity perturbation is damped; while $\alpha = 1$, the velocity perturbation holds critical stability. Using Eqs (4.1) and (4.2) with the expressions of the pressure perturbation attenuation of the TV and HLL-CPS-T schemes, it follows that

and from (4.5), we have

From (4.4) and (4.6) we can see that, if the velocity perturbation is damped $\left({0 < \alpha < 1} \right)$, then ${\hat u^\infty } = 0, {\hat p^\infty } = 0.$ The changes of the local velocity and pressure are zero in the flow direction, so $du = 0{\kern 1pt}$ and $dp = 0$. The equations indicate that the initial perturbation to the shear velocity and pressure fields decay over time and disappear completely, then the 'carbuncle' phenomenon is suppressed. Conversely, if the velocity perturbation is not damped $(\alpha = 1)$, then ${\hat u^\infty } = {\hat u^0}, {\hat p^\infty } = - {u_0}/2\upsilon{\hat u^0}$, the changes of the local velocity and pressure are not zero in the flow direction, $du \ne 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} dp \ne 0{\kern 1pt},$ and the 'carbuncle' phenomenon occurs. From the analysis of Section 4.1, we can get that the velocity perturbation of the HLL-CPS-T scheme is damped $(0 < \alpha < 1)$. It has enough numerical viscosity to suppress the disturbance parallel to the shock front and thus will not lead to the 'carbuncle' phenomenon and shock instability, while the velocity perturbation of the TV scheme is not damped $(\alpha = 1)$; it dose not have enough numerical viscosity to suppress the disturbance parallel to the shock front. Velocity perturbation will accumulate rapidly with the advance of the calculation process, which accelerates the shock instability, and the following numerical experiments will verify this conclusion.

5.   Numerical results

5.1.   Sod shock tube problem for Euler equations

The initial value condition is given in the region $x \in \left[{0, 1} \right]$ as

With Riemann boundary conditions, $CFL = 0.2$, grid number $N = 100$, calculated to $t = 0.{\rm{164}}$. As depicted in Figure 9, a comparison between the TV scheme and the HLL-CPS-T scheme with the exact solution reveals that the HLL-CPS-T scheme produces results that are closer to the exact solution than those obtained from the TV scheme, but they show varying degrees of smoothing at discontinuities, and the HLL-CPS-T scheme has fewer transition elements at the discontinuous corners, showing better resolution.

5.2.   The receding flow (vacuum) problem ${M_L} = - {M_R} = - 2$ ^[14]

The receding flow (vacuum) problem serves as a robustness test for a scheme. In this test, two parts of the fluid begin to recede from each other at $t = 0$, leading to a decrease in pressure and density in the middle region. The Roe scheme is known to fail in this test ^[14]. Figure 10 depicts that the HLL-CPS-T scheme has the ability to preserve positivity in pressure and density in this vacuum.

5.3.   Colliding shocks problem (${M_L} = - {M_R} = 25$) ^[14]

Now, let's examine the solution of two colliding shocks moving at $M$ = 25. As depicted in Figure 11, the HLL-CPS-T scheme yields monotonic profiles. The result of the TV scheme has fluctuation at both the shocks. Shock is little smeared in case of the TV scheme, showing very slight overshoots at the shoulder of the pressure profiles.

5.4.   The inviscid supersonic flow around a circular cylinder (${M_\infty } = 20$)

In ^[33], Quirk proposed that when performing numerical simulations, the occurrence of the 'carbuncle' phenomenon is more probable for high-Mach-number flows than for low-Mach-number flows. For this point, now we use the classical inviscid supersonic flow around a circular cylinder (${M_\infty } = 20$) to test the inference in Section 4. The calculation region is composed of two concentric circles with different radii 1 and 1.5, the initial values are $\rho = 8, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} u = 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} v = - 90, {\kern 1pt} {\kern 1pt} {\kern 1pt} p = 116.4,$ the angle is located between $2\pi /3$ and $4\pi /3$, it uses the uniform grid of $30 \times 300$ cells, the initial fluid height is $h = 1$, and the calculation ends with $t = 0.8$. The 'carbuncle' phenomenon is not only observed in the numerical simulation of supersonic flow over blunt bodies, but can also occur in other fluid dynamics problems. A detailed discussion on this issue can be found in reference ^[33]. Figure 12 shows the results of the two flux splitting schemes. For the TV scheme, as shown in Figure 12(a), we can see that a serious 'carbuncle' phenomenon occurs. For HLL-CPS-T, its velocity perturbation quickly decays to zero. As shown in Figure 12(b), HLL-CPS-T scheme can capture the shock front well, the instability is completely gone, and the flow field structure is clear and reasonable. Therefore, the inference of this paper is reasonable and effective.

5.5.   Shock diffraction over a ${90^0}$ corner (${M_\infty } = 5.09$)

Many low dissipation upwind methods have been reported to be failed in this problem. To simulate supersonic shock diffraction over a ${90^0}$ corner with Mach number 5.09, the computational domain is $[0, 1] \times [0.1, 0.9]$ and covered by a uniform structure grid $400 \times 320$. For convenience, the corner is selected at the midpoint of the left boundary, the left downside boundary and upper boundary are considered as solid walls, the left upside boundary is designed for inflow conditions, and the other boundaries are taken as outflow conditions. In the computation, the $CFL$ number is set to 0.95, computation ends with $t = 0.18$, and the initial conditions for the region to the right of the shock are $\rho = 1.4, p = 1/1.4, u = 0, and{\kern 1pt} {\kern 1pt} {\kern 1pt} v = 0{\rm{.}}$

Figure 13 shows the numerical results of the TV and HLL-CPS-T flux splitting schemes in solving the shock diffraction problem over a ${90^0}$ corner. We can see that the TV scheme appears as shock-unstable, while the HLL-CPS-T scheme can capture the shock well and appears as shock-stable. It is worth noting that in addition to the HLL-CPS scheme, the ability to attenuate velocity perturbations is a critical factor for achieving accurate and robust calculations in other upwind methods as well. After the analysis, we found that the method appears as shock-stable and robust, then its velocity perturbation is damped, while the others appear as shock-unstable because their velocity perturbations are not damped.

6.   Detailed theoretical comparison with the research of Sun et al. ^[26]

In the section, we will give a detailed theoretical comparison between our study and Sun et al. ^[26]. First, from the perspective of research objective, Sun et al. ^[26] utilized the HLL algorithm for the convective and pressure parts, incorporating a low dissipation modification to accurately capture the contact surface and extend the method for all speeds. Despite the similar treatment of the convective and pressure parts, our innovation lies in exploring a specific case of Sun et al. ^[26] when $f(M) = 1$ and conducting a detailed analysis of the numerical dissipation and shock stability of the scheme, thereby providing recommendations for the development of more robust upwind splitting schemes. Second, from the research methods and findings and through the analysis of the TV and HLL-CPS-T schemes' physical quantities' disturbance attenuation properties concerning Quirk's odd-even decoupling problem, we achieve the following: (1) We establish a sufficient condition to ensure shock stability for upwind methods. This conclusion can be used to analyze the shock stability of the existing upwind methods and as a basis to develop new types of shock-capturing methods. (2) The linear expressions for perturbed physical quantities in the TV and HLL-CPS-T methods are proposed in Table 1. We analyzed the response of the TV and HLL-CPS-T methods to Quirk's odd-even decoupling problem and identify the decay characteristics of the shock front normal velocity perturbation as the key factor determining whether the scheme produces the 'carbuncle' phenomenon, which differs from Pandolfi and D'Ambrosios' findings ^[23]. (3) We propose possible reasons for the occurrence of 'carbuncle' phenomenon in low dissipation schemes. It is worth noting that of the above three points, none of them were presented in ^[26]. Therefore, this paper serves as an extension and supplement to the work of Sun et al. ^[26].

7.   Conclusions

Based on Toro's splitting flux scheme and learned from the construction thought of Mandal's HLL-CPS method, a flux splitting scheme HLL-CPS-T was proposed which can accurately capture the contact discontinuity and shock. The new splitting scheme has been found to be more robust than the TV method, as it does not exhibit the 'carbuncle' phenomenon commonly observed in some other splitting schemes. Further, an inference is obtained: A sufficient condition to ensure shock stability for an upwind method is found to be that velocity perturbation is damped and ${u^\infty }$ is zero as the time step $k \to \infty$. The next step would be to conduct a comparative analysis between the HLL-CPS-T and other splitting schemes to validate its superiority. These comparative findings will be effectively showcased in our forthcoming research endeavors.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is funded by the National Nature Science Foundation (NNSF) of China (Grant Nos. 12071112, 11471102) and the Basic Research Projects for Key Scientific Research Projects in Henan Province (Grant No. 20ZX001).

Conflict of interest

The authors declare that they have no conflicts of interest.