Real-world validation of fractional-order model for COVID-19 vaccination impact

1.   Introduction

Mathematical representations capturing the dynamics of infectious disease transmission have become omnipresent. These representations serve a crucial function by quantifying potential strategies for the management and curtailment of infectious diseases ^[1,2,3]. Various models for infectious diseases are available, including compartmental models. These range from the foundational SIR model to more intricate propositions ^[4]. COVID-19, caused by the severe acute respiratory syndrome coronavirus 2, is an infectious ailment. It was initially recognized in December 2019 in Wuhan, the capital of Hubei, China. Since then, it has swiftly disseminated across the globe, leading to the continuous pandemic outbreak of 2020 ^[5]. Regarded as a paramount global menace, the COVID-19 pandemic has resulted in countless confirmed infections and a substantial number of fatalities worldwide. Note that, as of March 26, 2020, there were 503,274 confirmed cumulative cases with 22,342 fatalities. As of the present update, the figures have risen to 1,353,361 confirmed cumulative cases and 79,235 deaths, as indicated in the report from the World Health Organization dated April 8, 2020. Numerous researchers have engaged in the task of conceptualizing the propagation of COVID-19. One example involves Annas et al. who employed the SEIR model to delineate the intricate patterns of COVID-19 transmission within Indonesia ^[6]. Another instance is seen in the work of Darti et al., who employed the SI model to portray the diffusion of COVID-19 while considering a scenario in which a lockdown is in effect but citizens continue their daily routines ^[7]. Furthermore, Nuraini and colleagues extended their investigation by utilizing the SIQRD framework to elucidate the distribution of vaccines among a group of susceptible peoples ^[8]. Mukandavire et al. harnessed the SEIR model to assess the initial transmission of the COVID-19 outbreak in South Africa, and to investigate potential vaccine efficacy outcomes ^[9]. A comprehensive analysis of the COVID-19 spread and control model for China is presented as a reference ^[10]. Lastly, Diagne et al. employed the SVEAIHR model to elucidate the process of vaccinating a susceptible population at risk ^[11]. Hence, a range of mathematical frameworks have been devised to examine the transmission of COVID-19 in the context of vaccination. The authors of ^[12] studied a discrete fractional COVID-19 model and discussed its equilibrium point and stability results. Ahmad et al. ^[13] investigated a novel reaction diffusion model for the spread of COVID-19. Adel et al. ^[14] examined a COVID-19 mathematical model by applying a fractional technique in the sense of Caputo-Fabrizio. The mathematical disease models have been widely used in the study of fractional calculus, and its application has been explored in different areas, such as ^{[15,16,17,18,19]}.

Besides these works, fractional calculus has several applications in chaos theory, engineering, optics and other areas of science. For example, fractional-order bidirectional associative memory neural networks with delay are presented in ^[20], a fractional-order Myc/E2F/miR-17-92 network model is studied in ^[21], and there are also the fractional-order Jerk system with feedback controller ^[22], fractional-order three-triangle multi-delayed neural networks ^[23], bifurcations and a control mechanism for a fractional-order delayed Brusselator ^[24] and other works ^[25].

In their study, Ihsanjaya and Susyanto ^[26] constructed a model to depict the propagation of a COVID-19 outbreak while accounting for vaccination across vulnerable and healed people. This model categorizes the people into eight distinct groups. The vulnerable population is denoted as class $\mathcal{S}$, encompassing individuals vulnerable to COVID-19 infection. Those who have received vaccinations from the susceptible class are indicated as $\mathcal{V}_s$. The exposed class, $\mathcal{E}$, comprises individuals in the latent phase of infection. The asymptomatic infected class is labeled as $\mathcal{A}$, while the actively infected populace is represented by $\mathcal{I}$. Those requiring hospitalization fall into the class $\mathcal{H}$, whereas individuals who have recovered are designated as $\mathcal{R}$. Lastly, the vaccinated and recovered segment is denoted as $\mathcal{V}_R$. The governing system of ordinary differential equations is constructed through the utilization of the subsequent collection of differential equations:

with the following initial conditions:

The parameters used in the above model with description are given as follows: $\Lambda$ is the birth rate, $\mu_0$ represents the death rate, $\beta_1$ represents the rate of transmission between $\mathcal{S}$ and $\mathcal{A}$, $\beta_2$ represents the rate of transmission between $\mathcal{V}_s$ and $\mathcal{A}$, $\beta_3$ represents the rate of transmission between $\mathcal{R}$ and $\mathcal{A}$, $\beta_4$ represents the rate of transmission between $\mathcal{V}_R$ and $\mathcal{A}$, $\nu$ represents the vaccination rate of $\mathcal{S}$, the rate of vaccination of class $\mathcal{R}$ is represented by $\theta$, $d_1$ is the death rate from the disease, $d_2$ represents the death rate for the $\mathcal{H}$ class, $\omega$ represents the proportion of $\mathcal{E}$ that becomes infected, the rate at which the class $\mathcal{E}$ becomes infected is represented by $\gamma$, the rate at which the class $\mathcal{E}$ becomes infected is represented by $\alpha_1$, the rate of conversion from class $\mathcal{A}$ to $\mathcal{R}$ is $\alpha_2$, the rate of conversion from $\mathcal{A}$ to class $\mathcal{I}$ is represented by $\delta_1$, the rate of conversion from $\mathcal{I}$ to class $\mathcal{H}$ is represented by $\delta_2$ and the rate of recovery is represented by $\sigma$.

Moreover, in the deterministic model, the state of the epidemic model remains unaffected by its previous events. Nonetheless, in reality, memory assumes a critical role in comprehending the propagation patterns of epidemic diseases. To anticipate the trajectory of the coronavirus, Chen et al. ^[27] developed a dynamic system that incorporates fractional time delay. This system investigates the localized surges of COVID-19 outbreaks. Additionally, to enable the forecasting of potential outbreaks of contagious illnesses such as COVID-19 and other ailments, Xu et al. ^[28] introduced a comprehensive fractional-order SEIQRD model. In a related vein, Shaikh et al. ^[29] employed a fractional-order COVID-19 model centered on the transmission dynamics between bat hosts, reservoirs and human populations. This approach facilitated the assessment of preventive measures and diverse mitigation tactics, thereby forecasting forthcoming outbreaks and potential methods of control. Numerous research studies have explored various mathematical models related to diseases and finance, employing a range of techniques, such as ^{[30,31,32,33,34,35]}.

In this paper, the system under consideration, denoted as (1.1), is examined within the context of the Caputo fractional derivative. We transformed the integer-order model into a fractional-order model by using the Caputo operator. Fractional operators are versatile due to their additional degree of freedom and options. Consequently, we examined the system's dynamics across various fractional orders ranging from 0 to 1, comparing it to the integer-order case. Notably, stability was rapidly attained for lower fractional orders. Additionally, we conducted an investigation of the fractional model to assess the existence and uniqueness of its solutions. For the numerical simulation, the fractional Adams-Bashforth technique is used for the solution of the considered system. The presence of fractional-order operators in the equations of the system leads to an inherent imbalance in dimensional consistency between the left and right sides. In order to rectify this discrepancy, an auxiliary parameter $\varpi$ is introduced to modify the fractional operator. By assigning the dimension of seconds to $\varpi$, equilibrium is established in terms of dimensions on both sides of the equations ^[36]. Consequently, the Caputo fractional representation of the COVID-19 model as valid for $t > 0$ and an order within the range $\mathsf{d}\in(0 1]$, is defined as follows:

where ${^\mathit{C}}\mathbf{D}_t^\mathsf{d}$ represents the Caputo fractional derivative.

2.   Preliminary

The following definition recall is from ^[37].

Definition 2.1. The Caputo fractional-order derivative for a function $f(t)\in{H}^1(a, b)$ with order $n-1 < \mathsf{d}\leq{n}, \mathsf{d} > 0$ can written as

Definition 2.2. The Riemann-Liouville fractional integral for a function $f(t)$ having order $\mathsf{d}$ is given as

The Mittag-Leffler function for one parameter is defined as

and, for two parameters, it can be written as

3.   Analytical assessment of the governing model

This section uses fixed-point theory ideas to conduct a qualitative examination of the system under study. For the system represented by (1.2), we shall determine the existence and then the uniqueness of the solution. The provided model can be expressed in the subsequent format:

correspondingly,

and $\mathcal{U}_1, \mathcal{U}_2, \mathcal{U}_3, \mathcal{U}_4, \mathcal{U}_5, \mathcal{U}_6, \mathcal{U}_7, \mathcal{U}_8$ are respectively defined as

Upon integrating both sides of the aforementioned system (3.1), we obtain

Applying the aforementioned approach to each category outlined in (3.4), we get

Consequently, in order to demonstrate that the kernel $\mathcal{R}(\zeta, \mathcal{K}(\zeta))$ mitigates the Lipschitzian condition, along with the contraction, it suffices to establish the same property for all $\mathcal{U}_i$. With this foundation laid, we proceed to present the pivotal theorem of this paper.

Theorem 1. ^[38] Suppose that $\mathcal{U}_i$ serves to enhance the Lipschitzian condition with contraction for the bounded function $\mathcal{N}(t) = \mathcal{S}+\mathcal{V}_s+\mathcal{E}+\mathcal{A}+\mathcal{I}+\mathcal{H}+\mathcal{R}+\mathcal{V}_R$, provided that the subsequent inequality is satisfied:

where $\digamma_{i}$ represents constants. Furthermore, the solution to the system (1.2) remains both continuous and unique within a finite time $t_{1}$. Here, $t_{1}$ is defined as

Proof. Let the feasible region $\Psi = (\mathcal{S}+\mathcal{V}_s+\mathcal{E}+\mathcal{A}+\mathcal{I}+\mathcal{H}+\mathcal{R}+\mathcal{V}_R)\in\mathbf{R}^6\leq\frac{\Lambda}{\mu_0}.$ In the initial stage, our objective is to demonstrate the positivity and boundedness of $\mathcal{N} = \mathcal{S}+\mathcal{V}_s+\mathcal{E}+\mathcal{A}+\mathcal{I}+\mathcal{H}+\mathcal{R}+\mathcal{V}_R$. To achieve this, we sum up all of the equations from (1.2). This cumulative value of the population, involving the fractional operator, is denoted as

here, $\mathcal{N} = \mathcal{S}+\mathcal{V}_s+\mathcal{E}+\mathcal{A}+\mathcal{I}+\mathcal{H}+\mathcal{R}+\mathcal{V}_R.$ Through the utilization of the Laplace transform technique, we derive the population as

where $\mathbf{E}_{\mathsf{d}}$ represents the Mittag-Leffler function for one parameter and $\mathbf{E}_{\mathsf{d, d}}$ is the Mittag-Leffler for two parameters. After doing some calculation, the following is obtained, as mentioned also in ^[39]:

Thus, if $\mathcal{N}(0)\leq\frac{\Lambda}{\mu_0}$, then $t > 0$ and $\mathcal{N}(t)\leq\frac{\Lambda}{\mu_0}$. Next, we show the non-negativity of the aforementioned model:

Thus,

The solution of all compartments is positive; therefore, the solution of the considered system is bounded. Assuming an alternative solution for $\mathcal{S}$, denoted as $\mathcal{S}_1$, we can then deduce that

Let $\digamma_1 = \big(\beta_1a_4+\nu+\mu_0\big)$, where $\|\mathcal{A}(t)\|\leq a_4$ is bounded; thus,

As a result, the Lipschitz condition for $\mathcal{U}_1$ is achieved, and, if the inequality $1 > \big(\beta_1a_4+\nu+\mu_0\big)\geq{0}$ holds, then $\mathcal{U}_1$ demonstrates contraction properties. □

Similarly, we can also establish that $\mathcal{U}_i, \ \ i = 2, ..., 5$ must fulfill the Lipschitz condition, which is expressed as follows:

where $\digamma_{2} = \nu{a}_1+\beta_2{a_4}+\mu_0$, $\digamma_{3} = \beta_1{a_1}{a_4}+\beta_2{a_2}{a_4}+\beta_3{a_8}{a_4}+\gamma\omega+\gamma(1-\omega)+\mu_0+\mu_1$, $\digamma_{4} = \gamma(1-\omega){a_3}+(\alpha_1+\alpha_2+\mu_0)$, $\digamma_5 = \gamma\omega{a_3}+\alpha_2{a_4}+(\delta_1+\delta_2+\mu_0+{d_1})$, $\digamma_6 = \delta_1{a_5}+(\sigma\mu_0+{d_2})$, $\digamma_7 = \alpha_1{a_4}+\delta_2{a_5}+\sigma{a_6}+\beta_3{a_4}+(\mu_0+\theta)$ and $\digamma_{8} = \theta{a_7}+\beta_4{a_4}+\mu_0$; using (3.5), consider the subsequent recursive formulation:

with the following initial conditions: $\mathcal{S}(0) = \mathcal{S}_0, \ \ \mathcal{V}_s(0) = \mathcal{V}_{s(0)}, \ \ \mathcal{E}(0) = \mathcal{E}_{0}, \ \ \mathcal{A}(0) = \mathcal{A}_{0}, \ \ \mathcal{I}(0) = \mathcal{I}_{0}, \ \ \mathcal{H}(0) = \mathcal{H}_0, \ \ \mathcal{R}(0) = \mathcal{R}_{0}$ and $\mathcal{V}_R(0) = \mathcal{V}_{R(0)}.$ We proceed to apply the norm to the first equation as follows:

employing the Lipschitz condition, we obtain

Similarly,

Therefore,

Subsequently, we will establish the existence of solutions for the proposed model (1.2). Using a recursive technique, and from (3.15) and (3.16), we deduce that

Consequently, the presented problem possesses a solution, thus ensuring continuity. Moreover, we proceed to demonstrate that the aforementioned function constructs a solution for the system (1.2). Let us assume that

therefore,

After employing this approach once more, we obtain

At $t_1$, we have

As we take the limit of the above equation as $n$ approaches infinity, we arrive at $|\mathbb{J}_{1n}|\rightarrow {0}$. In a similar manner, we can establish the same result for $|\mathbb{J}_{in}|, i = 2, ..., 8.$ Thus, the proof is completed.

To establish the uniqueness of the solution, let us assume that the provided model possesses an alternative solution, denoted as $\mathcal{S}_1, \mathcal{V}_{s(1)}, \mathcal{E}_{1}, \mathcal{A}_{1}, \mathcal{I}_{1}, \mathcal{H}_1, \mathcal{R}_{1}$ and $\mathcal{V}_{R(1)}$. This leads us to the following:

by applying the norm to (3.20), we obtain

Utilizing the Lipschitz condition, we derive

Therefore,

Subsequently, we will establish that the given problem (1.2) possesses a unique solution under the condition that

Assume the satisfaction of the following condition:

Consequently, $\|\mathcal{S}-\mathcal{S}_1\| = 0$, implying that $\mathcal{S} = \mathcal{S}_1$. Similarly, following the same approach, we can demonstrate the following for the other categories: $\mathcal{V}_s, \mathcal{E}, \mathcal{A}, \mathcal{I}, \mathcal{H}, \mathcal{R}, \mathcal{V}_R.$

4.   Numerical scheme

In the forthcoming discussion, we demonstrate the general approach to solve the provided problem by utilizing the fractional Adams-Bashforth technique. We examine the model denoted as (1.2), while also recalling (3.5):

Initially, we extract the initial equation from the aforementioned system in order to formulate a numerical method. To achieve this, we contemplate the following:

In this context, we represent $t_{q}$ as $v\Delta$, where $v$ takes on values from 0 to $J$. Here, $\Delta = \frac{T}{J}$ represents the step size, with $J$ being a positive integer and $T$ a positive value. At the time point $t = t_{q+1}$, with corresponding $v$ values ranging from 0 to $J$, (4.2) can be expressed as follows:

and

Through the subtraction of (4.4) from (4.3), we have

we express the equation above in the same manner:

where

Upon applying Lagrangian polynomial interpolation, the approximated function $\mathcal{U}_1(\mathcal{S}, t)$ takes the form

thus,

by simplifying the integrals involving the right-hand side of the equation above, we have

Similarly,

Substituting the values of $\mathscr{G}_{\mathsf{d}, 1}$ and $\mathscr{G}_{\mathsf{d}, 2}$ into (4.5), we can have the subsequent approximate solution for the first equation:

Similarly, for the remaining equations, we obtain

The Eqs (4.10)–(4.17) presented above constitute the solution for the system (1.2).

4.1.   Simulation and discussion of the stability results

This section presents numerical illustrations of the acquired outcomes. For the simulations, the initial values were obtained from ^[26] as $[\mathcal{S}, \mathcal{V}_{s}, \mathcal{E}, \mathcal{A}, \mathcal{I}, \mathcal{H}, \mathcal{R}, \mathcal{V}_{R}]$ = $[100000, 50000,150,100,150, 45,259, 35]$. The parameter values were assumed as indicated in Table 1.

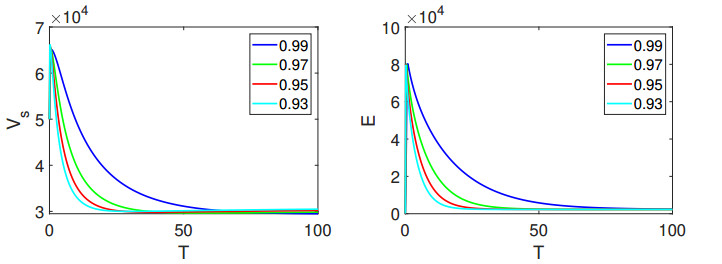
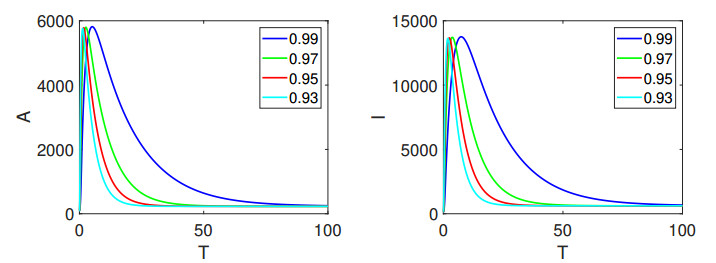
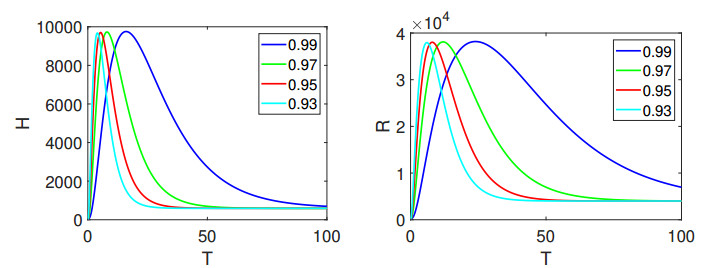
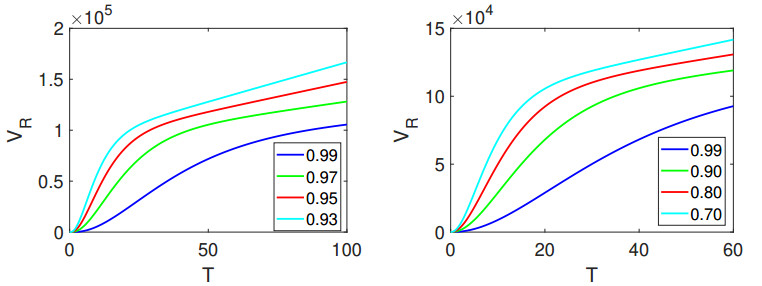
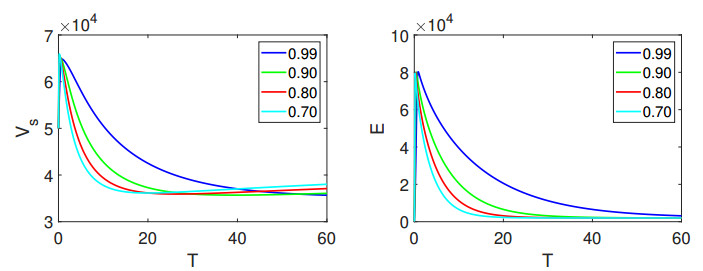
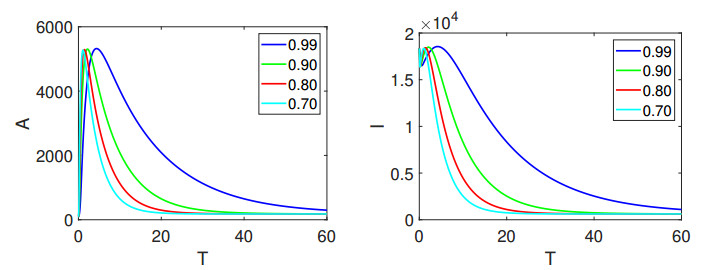
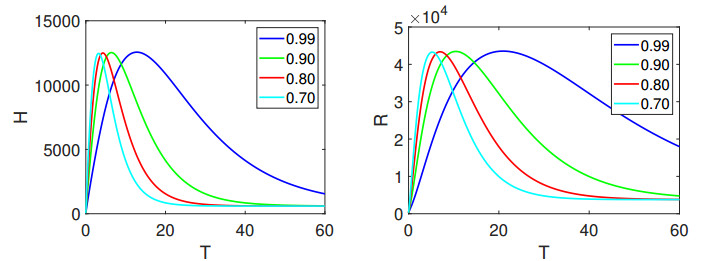
In Figure 1, the left panel vividly portrays the dynamic behavior of the state variable $\mathcal{V}_{{s}},$ while the right panel offers visual insight into the evolution of $\mathcal{E}.$ Further elucidating the dynamics, Figure 2 provides comprehensive depictions of $\mathcal{A}$ and $\mathcal{I},$ respectively. The visual narrative continues in Figure 3, where we observe the ever-changing nature of $\mathcal{H}$ and $\mathcal{R},$ offering a holistic view of the model's dynamics. Additionally, the intriguing interplay between vaccination unfolds in Figure 4, with high as well as lower fractional orders and where the number of vaccinated individuals in the recovered population is clearly illustrated. Similarly, Figures 5–7 show the visualization of the classes of system (1.2) with lower fractional orders, where we see that the dynamics become stable in a shorter time than for the high orders.

Upon careful examination of these simulations, it becomes apparent that the initially recovered individuals due to vaccination are fewer in number compared to those who recover without vaccination. However, what stands out is the gradual but steady rise in the population of $\mathcal{V}_{{R}}$, underscoring the paramount significance of widespread vaccination efforts in promoting public health and minimizing disease transmission.

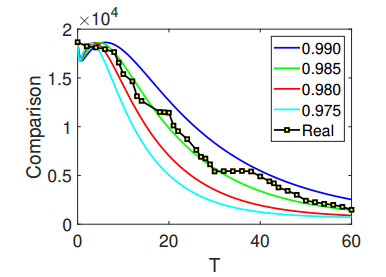
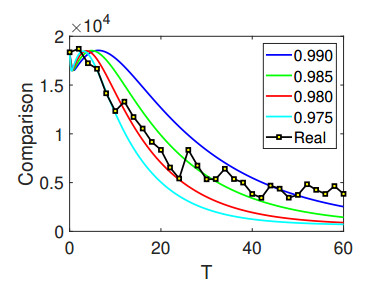
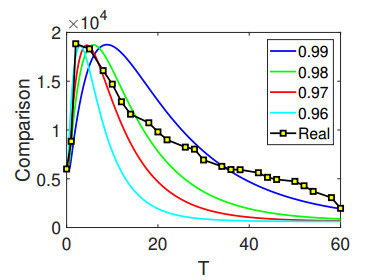
The results visualized in Figures 8–10 present comparisons between the results with different fractional orders and real data from various countries, which include India, Australia and the UK. The data were sourced from ^[5], covering various time periods for every country: July 31 to September 30 in 2022 for Australia, July 31 to September 28 for India and July 10 to September 8 for the UK.

Notably, it is crucial to acknowledge that the first figure's real data demonstrate an equivalence between 1000 and 2000, as revealed in the comparison. The simulations were conducted with a step size of $dt = 0.01$, incorporating different initial values of $\mathcal{I}$, while the other initial conditions were applied as presented earlier. The parameters for the comparisons of the real data with the simulated results were considered as presented in Table 1.

Upon meticulous examination of the acquired outcomes, it becomes evident that the actual data and the simulated results align remarkably well, particularly for India and Spain. A substantial majority of data points from the real dataset precisely corresponds with the outcomes of our simulations. This underscores the profound impact of stochastic dynamics in the analysis of biological models, as well as its ability to yield reliable and dependable findings. These findings are invaluable for understanding the complexities of the observed biological phenomena, and they can inform further research and decision-making processes.

5.   Conclusions

Our study introduces a novel fractional-order mathematical framework that enhances our understanding of the dynamics underlying COVID-19 outbreaks and the impact of vaccination strategies. Through the formulation of a system involving eight nonlinear fractional-order differential equations in the Caputo sense, we have successfully captured the intricacies of disease transmission. The utilization of the fixed-point technique confirms the existence and uniqueness of solutions for our proposed model. By employing the fractional Adams-Bashforth numerical method, we have delved into both the approximate solutions and the dynamic behaviors intrinsic to our model. Importantly, our work is distinguished by its meticulous consideration of dimensional consistency throughout the fractionalization process, setting it apart from recent studies in this field. The obtained results are numerically demonstrated. Moreover, the comparison of the real data with simulated results reveals that the proposed work is very effective, as most of the points of real data coincided with the simulated results. In the future, this work can be further studied by using neural networks and other methods ^[42,43,44].

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research (IFKSUOR3–244-3).

Conflict of interest

The authors declare no conflict of interest.