1.
Introduction
The stress-strength reliability model is a widely used probabilistic indicator that demonstrates the effectiveness of a system. By employing this model, it is possible to calculate the probability of failure for components. This model is crucial in various real-world domains such as engineering, business, medicine, and quality assurance. The likelihood that the random strength X of a component will be greater than the random stress Y is measured by the stress-strength index R=P(Y<X), see Kotz et al. [1]. Comparing the lifetimes of the two devices, denoted by X and Y, is another significant use of the stress-strength reliability model. Many writers have extensively discussed the inference issues related to the stress-strength index R. For example, one can refer to Kundu and Gupta [2] and Krishnamoorthy et al. [3]. They used the complete sample data to study the stress-strength index R from generalized exponential and two-parameter exponential distributions, respectively. Recent research has concentrated on assessing the stress-strength index R using different censored samples and employing both classical and Bayesian estimation methods. This shift in focus is due to the impracticality of utilizing complete data for this purpose, especially when the tested components are reliable. In this regard, Asgharzadeh et al. [4] studied the stress-strength model of Weibull progressively censored data. Yadav et al. [5] considered the stress-strength model of inverse Weibull progressively censored samples. Bai et al. [6] investigated some estimations of the stress-strength model based on finite mixture distributions in the case of progressive interval censoring. Ghanbari et al. [7] studied the stress–strength reliability for Marshall–Olkin distributions using progressive Type-Ⅱ censoring. Nassar et al. [8] considered the spacings estimation of the reliability index for alpha power exponential distribution progressive Type-Ⅱ censored data. Sultana et al. [9] assessed the reliability parameter using two-sample balanced progressively censored samples.
Choosing a suitable statistical distribution to characterize the random variables X and Y is essential for estimating the stress-strength metric R. To accurately compute R, the most suitable statistical model needs to be carefully selected. For this investigation, we assume that the random variables X and Y are independent and have a new extended xgamma (EXG) distribution. The EXG distribution was proposed and studied by Sen et al. [10]. It is also known as the Mirra distribution. The EXG distribution is a finite mixture of the exponential distribution with scale parameter λ and the gamma distribution with scale parameter λ and shape parameter equal to 3, with mixing proportions λ2/(β+λ2) and α/(β+λ2), respectively. Thus, we can say that the random variable X follows the EXG distribution with parameters λ,β>0 if its probability density function (PDF) and cumulative distribution function (CDF) are given by
and
By setting λ=β in (1.1), one can acquire the xgamma distribution proposed by Sen et al. [11]. Sen et al. [10] demonstrated that the EXG distribution is an effective model for data exhibiting a bathtub hazard rate shape as well as increasing and decreasing shapes based on certain ranges of x. For example, infants experience a high failure rate due to health issues, but this rate decreases as they grow older. However, in later years, failure rates increase again due to age-related health problems, resulting in a bathtub-shaped curve. The failure rate of batteries generally increases with age and the number of charge cycles, leading to an increasing hazard rate shape. Many semiconductor devices suffer early failures because of defects. However, after this initial period, the remaining devices often operate reliably, resulting in a decrease in failure rates over time. They also showed that the EXG distribution is superior to some commonly used models, such as the xgamma, gamma, Weibull, log-normal, and exponentiated exponential distributions, among others. Peres [12] investigated some applications of the EXG distribution in survival analysis. When X∼EXG(λ,β1) and Y∼EXG(λ,β2), where X represents the strength of a component and Y is the applied stress, the reliability index R=P(Y<X) can be derived as shown by Sen et al. [10] as follows:
In reliability investigations, the use of censoring plans is common, enabling the experimenter to end the test earlier before all of the items fail. These procedures result in data referred to as censored data. Among the different censorship plans accessible in the literature, first-failure censoring is a type of life test in which the researcher divides the items into distinct groups, each functioning as a cluster of test items, and subsequently conducts the test for all of the groups together until the first failure in each of them is detected. The sample items, denoted by N, can be examined with the formula N=k×n, where n is the number of groups, each one with an identical amount of items k. It is beneficial when the survival period is extremely long and the testing capabilities are restricted, but test material is significantly less expensive. The major disadvantage of the first failure censoring is that it prohibits items from being removed at any moment other than the scheduled ending time. To address this issue, Wu and Ku [13] developed the so-called progressive first-failure censoring (PFFC) plan. This scheme can be outlined as follows: Assume that there are n distinct sets, each containing k items, assigned to a life-testing experiment at time zero. Let r be the preset number of failures and S=(S1,…,Sr) represent the prefixed removal pattern. Then, at the time of the first failure, denoted by X1:r, S1 sets are removed from the test, as is the set from which the first failure happened. After detecting the second failure, with failure time X2:r, S2 sets, as well as the set that experienced the second failure, are eliminated from the still-living sets, and so forth. The process proceeds until the r−th failure arises, with failure time Xr:r, and at this point, all the leftover sets Sr=n−r−∑r−1i=1Si are eliminated from the test. Consider x_=(x1,…,xr) as the realization of X1:r,…,Xr:r. Then, based on a PFFC sample x_ with a progressive censoring plan S taken from a continuous population with PDF h(.) and CDF H(.), one can write the joint likelihood function of the observed sample as given below:
where θ is the unknown parameters vector and C is a constant. It is important to mention here that by setting k=1, the progressive Type-Ⅱ censoring can be acquired as special case from (1.4). Several studies explored the inferences of some lifetime models employing the PFFC scheme. For example, the Gompertz distribution by Soliman et al. [14], Lindley distribution by Dube et al. [15], generalized inverted exponential distribution by Ahmed [16], generalized Maxwell failure by Saini et al. [17], Nadarajah–Haghighi distribution by Ashour et al. [18], inverse power Lomax distribution by Shi and Shi [19], log-logistic distribution by Xie and Gui [20], left-truncated normal distribution by Cai and Gui [21], alpha power exponential distribution by Nassar et al. [22], and generalized extreme value distribution by Elshahhat et al. [23].
The flexible hazard rate function provided by the EXG distribution is desirable in analyzing various kinds of data, but there has been little interest in estimating the model parameters or functions that include them, especially for censoring samples. From a practical perspective, as indicated later in the data analysis section, the results demonstrate that the EXG distribution is suitable for modeling the time to breakdown of insulating fluid data. Additionally, no previous research has examined the classical and Bayesian estimation concerns related to the EXG distribution. The only available study by Sen et al. [10] focused on classical estimation of the EXG distribution using a complete sample. However, this study does not address Bayesian estimation of the unknown parameters or the estimation methods for censored samples. Given these reasons, we recommend using the PFFC samples to estimate the EXG distribution. This choice is motivated by the fact that it can encompass various conventional censoring plans, such as progressive Type-Ⅱ and Type-Ⅱ censorship schemes. It is important to mention here that the results of classical estimation by Sen et al. [10] can be viewed as a special case of the current study. Our primary focus is on estimating the unknown parameters, followed by the stress-strength index R=P(Y<X). We believe that this topic will be helpful to a wide range of readers, particularly reliability engineers and statisticians. The main objectives of this study are as follows:
1) Finding the maximum likelihood estimates (MLEs) and approximate confidence intervals (ACIs) for model parameters λ, β1, and β2. Additionally, we utilize the invariance property to compute the MLE of the stress-strength index R=P(Y<X). The ACI of R is also calculated using the delta approach to approximate the variance of the MLE of R.
2) Investigating Bayesian estimations of λ, β1, and β2, as well as R=P(Y<X) using the squared error (SE) loss function. To address the challenges posed by the joint posterior distribution form, we calculate Bayes estimates by sampling from the posterior distribution using the Markov chain Monte Carlo (MCMC) approach. Additionally, we explore the Bayes credible intervals (BCIs) for different parameters.
3) Comparing the various obtained estimates helps identify which strategy produces adequate estimates for the EXG distribution. To attain this goal, we conduct simulation research using several experimental designs and statistical precision requirements.
4) In order to ensure that the results provided are grounded in real-life observations rather than simulations only, and to enhance the identification and resolution of real-world issues, two sets of insulating fluid data are investigated. This analysis aims to observe the actual patterns and applicability of the different estimates.
The article will be arranged as follows. Section 2 investigates the MLEs of λ, β1, β2, and the stress-strength index R, and the associated ACIs. In Section 3, we use the MCMC procedure to calculate Bayesian estimates of the various parameters, incorporating the SSE loss function, as well as the BCIs. Section 4 includes the design and findings of the simulation study. Section 5 evaluates two insulating fluid data sets. Finally, we conclude the paper in Section 6.
2.
Classical inference
For the EXG distribution and based on PFFC samples, the maximum likelihood estimations for the various parameters, namely λ, β1, β2, and the reliability index R, are investigated in this section. Along with the point estimations, the interval estimations are also discussed.
2.1. Point estimation
Let x_=(x1,…,xr) be an observed PFFC sample of size r out of n groups taken from the EXG(λ,β1) population with removal plan S=(S1,…,Sr). Moreover, let Let y_=(y1,…,ym) be an observed PFFC sample of size m out of v groups selected from the EXG(λ,β2) population with removal pattern R=(R1,…,Rm). Based on the observed data, the joint likelihood function can be formulated as
where θ=(λ,β1,β2)⊤. Using (1.1), (1.2), and (2.1), the likelihood function, ignoring the constant term, we have
where κ=r+m+2(k1n+k2v), Q1i=k1(1+Si), Q2i=k2(1+Ri), ψi(xi;λ)=1λ2+xiλ+0.5x2i. The natural logarithm of (2.2), indicated by L(θ|x_,y_), can be expressed as
From (2.3), the maximum likelihood estimates (MLEs) of λ, β1, and β2 can be obtained through solving the next three normal equations simultaneously:
and
where ψ1i(xi;λ)=xiλ2+2λ3. Upon initial examination of the normal equations, it is evident that explicit expressions for the MLEs are not present. Therefore, it is necessary to utilize numerical techniques in order to obtain the MLEs, indicated by ˆλ, ˆβ1, and ˆβ2. Once we have calculated the MLEs of the unknown parameters, we can leverage the invariance property to calculate the MLE of the reliability index R that we need. This is done in the following manner:
2.2. Interval estimation
In this part, we first construct the ACIs for the parameters λ, β1, and β2. We then use the same method to determine the interval bounds for the reliability index R. The ACIs for the parameters λ, β1, and β2 are determined depending on the asymptotic normality of the MLEs, which indicates that (ˆλ,ˆβ1,ˆβ2)∼N[(λ,β1,β2),J(θ)], on which J(θ) represents the variance-covariance matrix acquired through obtaining the inverse of the Fisher information matrix. In our case, computing the exact expressions of the Fisher information matrix is challenging due to their complexity. As a result, we overcome this difficulty by estimating the variance-covariance matrix through the inversion of the observed Fisher information matrix, as illustrated below:
where all derivatives in (2.7) are evaluated at the MLEs ˆλ, ˆβ1, and ˆβ2, and
and
According on the asymptotic normality of the MLEs, the 100(1−α)% ACIs of λ, β1, and β2 can be computed as
where zα/2 is the upper (α/2)th percentile point of the standard normal distribution.
In order to calculate the ACI ranges of the reliability index R, we must first determine the variance of ˆR. To do this, we use the estimated variance-covariance matrix in Eq (2.7) and apply the delta method to approximate the estimated variance of ˆR as
where
After obtaining ^var(ˆR), we can simply compute 100%(1−α) ACI of the reliability index R as
3.
Bayesian inference
In this section, we will use the Bayesian estimation approach to study the Bayes estimates for the unknown parameters λ, β1, and β2, as well as the reliability index R of the EXG distribution, based on PFFC data. We provide a simple comparison of the advantages and disadvantages of maximum likelihood and Bayesian inferential approaches, as follows:
(a) Maximum likelihood estimation
(ⅰ) Advantages:
● It provides the best and most effective parameter estimator when the correct model assumptions are employed.
● It can provide the user with a consistent and adaptable approach, making it more dependable than other estimators.
● For large samples, it delivers unbiased results.
(ⅱ) Disadvantages:
● It becomes highly sensitive to the choice of a model's initial values, creating significant challenges similar to those faced by other methods.
● The computational cost of numerical estimating may increase due to the complexity of the normal equations.
● For a small sample size, it generates inaccurate results.
(b) Bayesian estimation
(ⅰ) Advantages:
● It provides a clear and principled way to integrate prior knowledge with data.
● It gives conditional and accurate conclusions based on data.
● It follows the principle of probability.
● It gives interpretable results.
● It offers a suitable environment for a variety of models, including hierarchical models and missing data issues.
● It is highly dependent on MCMC techniques and makes computations tractable for nearly all parametric models.
(ⅱ) Disadvantages:
● The specification of a suitable prior is very hard.
● It can generate posterior distributions that are significantly influenced by the priors.
● It often requires intensive computations.
3.1. Prior selection and posterior distribution
To begin the Bayesian approach, we need to specify our knowledge of the unknown parameters λ, β1, and β2 using prior distributions. Since there are no conjugate priors available for the EXG distribution, we use the gamma distribution to reflect the prior knowledge for the three unknown parameters. We assume that these parameters are independent, with each following the gamma prior distribution. This selection can be justified through the following: The gamma distribution is flexible and can model a wide variety of shapes depending on the value of its shape parameter. It has the same support as the true unknown parameters λ, β1, and β2. It is commonly used in practice, facilitating both analytical and numerical Bayesian analysis. The closed-form expressions for both the mean and variance of the gamma distribution allow for easy determination of hyper-parameter values during simulations and data analysis. Additionally, the closed form of its variance enables an examination of how the degree of variation in the prior distribution influences estimation performance. The joint prior distribution in this case can be expressed as
where τj,ωj>0,j=1,2,3 are the hyper-parameters and assumed to be known. Combining the likelihood function in Eq (2.2) with the joint prior distribution in Eq (3.1), the posterior distribution of λ, β1, and β2 can possibly be presented as
where A refers to the normalized constant.
The loss function is an important component of Bayesian analysis. There are several loss functions found in the literature. For this study, we specifically employ the symmetric SE loss function to calculate the necessary Bayes estimators. In this case, the Bayes estimator is obtained by as the posterior distribution mean. The Bayes estimator for any parametric function, denoted as ϖ(θ), using the SE loss function, can be obtained from the posterior distribution in (3.2) as
Equation (3.3) reveals a challenge in obtaining the Bayes estimator. This challenge arises from the difficulty of obtaining the ratio of integrals.
3.2. MCMC sampling strategy
To overcome the difficulty of obtaining the Bayes estimator in (3.3), we propose utilizing the technique of MCMC. The purpose of MCMC is to simulate samples from the posterior distribution, which can then be used to compute the necessary Bayes estimates and BCIs. To apply the MCMC technique, we follow the next two steps:
1) Determine the full conditional distributions of the various unknown parameters. The conditional distributions of the parameters λ, β1, and β2 can be obtained by retaining only the terms that depend on the specific parameter of interest. From (3.2), we have
and
2) Determine if the conditional distributions can be simplified to any known distributions. This is an important step in deciding which algorithm to use for generating the samples. The conditional distributions in (3.4)–(3.6) are unidentified and cannot be represented by any established distributions.
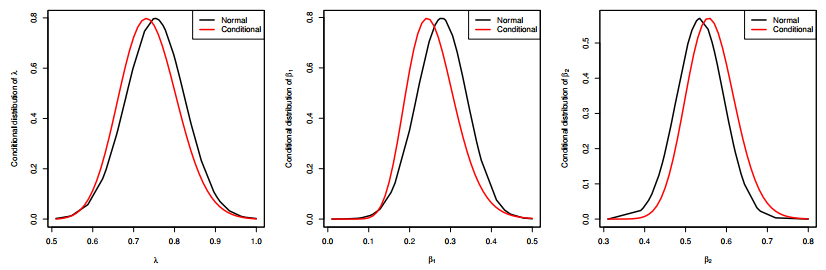
By simulating a random sample from the proposed censored strategy using (β1,β2,λ)=(0.2,0.5,0.8), when k1=k2=2, n=v=100, r=m=50, and S=R (uniform progressive design), Figure 1 indicates that the proposed conditional distribution of λ, β1, or β2 behaves similar to a normal distribution. Therefore, we employ the Metropolis-Hastings (MH) procedure with a normal proposal distribution to obtain samples from these distributions.
The following steps illustrate how the MH algorithm generates the required samples
Step 1. Take j=1 and make use of (λ(0),β(0)1,β(0)2)=(ˆλ1,ˆβ1,ˆβ1) as starting choices.
Step 2. Use the MH steps to simulate:
● λ(j) from (3.4) with N(λ(j−1),^var(ˆλ)).
● β(j)1 from (3.5) with N(β(j−1)1,^var(^β1)).
● β(j)2 from (3.6) with N(β(j−1)2,^var(^β2)).
Step 3. Employ the simulated values (λ(j),β(j)1,β(j)2) to obtain R(j) as
Step 4. Set j=j+1 and perform steps 2 and 3, M times to generate
After obtaining the MCMC samples, we can use them to compute the Bayes estimates and associated BCIs. To ensure that the derived estimates are trustworthy, the impact of the initial values must be removed first. This can be achieved by removing the first K generated samples, which is known as the burn-in phase. After discarding the K samples, we will have (λ(j),β(j)1,β(j)2,R(j)) for j=K+1,…,M. We can then compute the Bayes estimates for the various parameters as well as the reliability index using the SE loss function as
where ˉM=M−K. On the other hand, after sorting (λ(j),β(j)1,β(j)2,R(j)) as (λ[j],β[j]1,β[j]2,R(j)) for j=K+1,…,M, we can obtain the 100%(1−α) BCIs as
4.
Monte Carlo comparisons
This section compares the offered point and interval estimators of β1, β2, λ, and R based on a series of Monte Carlo simulations.
4.1. Simulation designs
We replicated 1,000 times PFFC data from the proposed EXG model when (β1,β2,λ)=(0.2,0.5,0.8). Taking k(=2,4), where k1=k2=k, several predetermined values of n,v (number of groups), r,m (effective sample sizes), and S,R (removal plans) are used; see Table 1. Specifically, for each value of k, n, and v, the values of r (or m) are utilized as a failure percentage (FP), such as rn=mv=50 and 80%. Without loss of generality, in Table 1, we assumed that the comparison setups used for the EXG(λ,β1) and EXG(λ,β2) populations are the same. To distinguish, in Table 1, the progressive design (115) (as an example) means that one survival item will be drawn fifteen times. Then, once 1000 PFFC samples are available, there are two recommended packages called 'maxLik' (by Henningsen and Toomet [24]) and 'coda' (by Plummer et al. [25]) which are utilized to calculate the frequentist and Bayes estimations.
Specifically, to gather a PFFC sample of sizes r and m from the EXG(λ,β1) and EXG(λ,β2) populations, respectively, do the following steps:
Step 1: Set the true values of EXG(λ,β1) population.
Step 2: Obtain a conventional progressive Type-Ⅱ sample as follows:
(a) Obtain ϱ independent items (say ϱ1,ϱ2,…,ϱr) from a uniform U(0,1) distribution.
(b) Set ξi=ϱ(i+∑rj=r−i+1Rj)−1i for i=1,2,…,r.
(c) Set Ui=1−ξrξr−1⋯ξr−i+1 for i=1,2,…,r.
(d) Collect a desired progressive Type-Ⅱ sample (with size r) from the EXG(λ,β1) distribution by taking:
Step 3: Group each data set of X∗i for i=1,2,…,r randomly into other sets of size k.
Step 4: Collect a PFFC sample by setting Xi=min{X∗i} for i=1,2,…,r.
Step 5: Redo steps 1–4 for the EXG(λ,β2) population.
In this study, we use the Newton-Raphson method to compute the MLEs of the unknown parameters λ, β1, and β2. The method can be applied by following these steps:
1) Determine the score function Δ(λ,β1,β2)=(∂L(θ|x_,y_)∂λ,∂L(θ|x_,y_)∂β1,∂L(θ|x_,y_)∂β2)⊤.
2) Obtain the Hessian matrix J(λ,β1,β2) with second-order partial derivatives as provided in subsection 2.2.
3) Use the initial values (λ(0),β(0)1,β(0)2) to update the estimates iteratively as
4) Continue the process until convergence is achieved.
To implement the Newton-Raphson method, we utilize the 'maxLik' package (developed by Henningsen and Toomet [24]) which employs the 'maxNR()' function of maximization in the R programming language.
By considering two criteria of prior density, namely prior mean and prior variance, we use two informative sets of the prior-parameters τj,ωj>0 for j=1,2,3, called Prior-1:(τ1,τ2,τ3)=(1,2.5,4) and ωj=5 for j=1,2,3, and Prior-2:(τ1,τ2,τ3)=(2,5,8) and ωj=10 for j=1,2,3. According to the MH procedure prescribed in Section 3, we draw MCMC samples of size M=12,000 and discard the first K=2,000 samples. Subsequently, when ˉM=10,000, all Bayes' findings are evaluated.
The obtained estimate serves as an approximation of the theoretical expression for an unknown parameter. Its accuracy reflects the reproducibility of the estimate and indicates its proximity to the true value. Therefore, for each PFFC data set derived from the EXG(λ,β1) and EXG(λ,β2) populations, we calculate the following measures of R (as an example) to judge the performance of the obtained estimates:
● The average estimate (AvE) of R (say, ¯¨R) is given by
● Root mean squared-error (RMSE):
● Mean relative absolute bias (MRAB):
● Average interval length (AIL):
● Coverage percentage (CP):
where ¨R[d] is the calculated estimate of R at the dth sample, 1(⋅) is the indicator function, and (L(⋅), U(⋅)) refers to (lower, upper) interval bounds.
4.2. Simulation outputs
All simulation results of β1, β2, λ, and R are reported in Tables 2–9. For specification, in Tables 2–5, the AvE, RMSEs, and MRABs are listed in the first, second, and third columns, respectively. Additionally, in Tables 6–9, the AILs and CPs are listed in the first and second, respectively.
From Tables 2–9, in sense of the lowest RMSE, MRAB, and AILs as well as the largest CPs, we list the following notes:
● The best of our observation is that the offered estimates of β1, β2, λ, or R behave satisfactorily in the presence of the proposed data.
● When v(or n) grows, all results of β1, β2, λ, or R perform well. This fact means that the offered MLE results of β1, β2, λ, or R are consistent. This result is also observed when ∑ri=1Si (or ∑mi=1Ri) decreases.
● Because the Bayes results included more precision information from the joint gamma prior, as we anticipated, the Bayesian estimations of β1, β2, λ, and R behaved better compared to the frequentist estimates. The same conclusion is also reached if one compares the asymptotic intervals with credible intervals.
● It is evident from comparing the provided priors 1 and 2 that the Bayes estimates based on Prior-2 outperform the other estimates due to the variance associated with Prior-2 being less than the other.
● As k grows, the simulated RMSE, MRAB, and AIL values for all results of β2, λ, and R increase, while those of β1 decrease.
● As k grows, the simulated CP values for all results of β2, λ, and R decrease while those of β1 increase.
● It is clear, in most cases, that the estimated CPs of ACI/BCI estimates are almost closely (or greater) to the preassigned nominal level 95%.
● Comparing the PC[i] for i=1,2,3,4, the inferential results of β1 and β2 become superiority based on PC[4] and PC[2], respectively, while those of λ, and R become superiority based on PC[1].
● As a recommendation, to receive efficient inferential results about β1, β2, λ, or R in the presence of PFFC data, the investigator ought to increase the number of groups.
5.
Insulating fluid data analysis
This section addresses two distinct engineering applications to demonstrate the practicality of the suggested estimators and the usefulness of the offered estimation techniques. Both applications analyze the time to breakdown of an insulating fluid (in seconds) during a voltage endurance test under various stress conditions. We now list the following insulating fluid data sets as follows:
● The first data set, called Data-A, consists of two pressure levels, namely 40kV (with n=12) and 45kV (with v=12). This type of data was reported by Nelson [26] and discussed by Nassar et al. [27]. By denoting that the data set at 40kV by X and at 45kV by Y, in Table 10, each time point has been divided by ten for the computational process.
● The second data set, called Data-B, consists of two pressure levels, namely: 30kV (with n=10) and 36kV (with v=15); see Nelson [26] and Alotaibi et al. [28]. Here, we denote the data set at 30kV by X and at 36kV by Y, then each time is divided by 100 for computational ease; see Table 10.
Before proceeding with our inference, to determine whether or not the EXG model provides a significant fit to the insulating fluid data sets, we evaluate the Kolmogorov-Smirnov (KS) statistic and P-value at a 5% significance level; see Table 11. Additionally, the MLEs with associated standard-errors (St.Er) of EXG parameters are also obtained and provided in Table 11. Since the P-value results are higher than 5%, we can decide that the proposed EXG distribution fits the insulating fluid data sets satisfactorily.
In Figure 2, we employ three visual aids to demonstrate the performance of fitting the proposed EXG model to insulating fluid data sets; namely: (ⅰ) contour diagrams of the log-likelihood, and (ⅱ) estimated/empirical reliability. It can be seen that:
● The contour plots using the complete data sets state that the MLEs of EXG parameters exist and are unique.
● The estimated EXG reliability line is close to its empirical line.
From Table 10, for each data set, the first-failure censored sample is generated by randomly grouping and taking k=2 and 3 for groups X and Y, respectively; see Table 12. To distinguish, the starred number refers to the first-failure item. As a result, from Table 12, the first-failure censored samples are presented in Table 13. Taking (r,m)=(3,3), using Table 13, we report different PFFC samples in Table 14 based on various choices of R and S. Via the MH sampler, with M=50,000 and K=10,000, the Bayes evaluations of β1, β2, λ, and R are developed using non-informative prior. Hence, the point estimations (with their St.Ers) and 95% interval estimations (with their widths of β1, β2, λ, and R are obtained; see Tables 15 and 16. It shows that the estimated point values of β1, β2, λ, and R obtained by both likelihood and Bayesian estimation methods are quite similar. It also indicates that the Bayes point (or 95% BCI) findings of all unknown quantities outperform those developed by the likelihood approach in terms of the minimum level of standard-error and shortest interval values.
When using the maximum likelihood estimation approach, existence and uniqueness are important features to highlight when obtaining the MLEs. Using sample-I (as an example) from Table 14, the profile log-likelihoods of β1, β2, and λ are plotted; see Figure 3. It shows that the calculated values of β1, β2, and λ (in Table 15) exist and are unique. Again, using sample-I (as an example) from Table 14, Figure 4 displays both trace and density plots of β1, β2, λ, and R using their staying ˉM=40,000 iterations. It demonstrates that the collected iterations of β1, β2, λ, and R are roughly symmetric and mixed effectively. For clarity, in Figure 4, the sample mean and 95% BCI bounds of β1, β2, λ, and R are represented by solid red and red–dashed lines, respectively.
6.
Conclusions
This study explored different techniques for evaluating the stress-strength index based on progressively first-failure censored data. We consider the strength and stress factors as independent random variables, modeled using extended xgamma distributions. The model parameters and the stress-strength index using the maximum likelihood method, a widely used approach, are addressed. Additionally, the approximate confidence intervals for these estimations are obtained. To approximate the variance of the classical estimator of the stress-strength index, we employed the delta method. Furthermore, the gamma priors and the squared error loss function are utilized to estimate the Bayes estimates of the model parameters and stress-strength index. The Markov chain Monte Carlo approach is used to generate samples from conditional distributions, which allows for the calculation of Bayesian estimates considering the complex nature of the posterior distribution. Additionally, Bayesian credible ranges are calculated. To assess the estimations, we conducted a thorough numerical study with numerous testing methodologies. We employed the various approaches for analyzing a pair of insulating fluid data sets, seeking to increase our comprehension and demonstrate the applicability of the supplied estimations. For future research, one can investigate the same estimation approaches discussed in this study for the stress-strength index of the extended xgamma distribution in the context of progressively first-failure censored data when all parameters are unequal.
Author contributions
Refah Alotaibi: Conceptualization, Methodology, Investigation, Funding acquisition, Writing–original draft; Mazen Nassar: Conceptualization, Methodology, Investigation, Writing–review & editing; Zareen A. Khan: Conceptualization, Investigation; Ahmed Elshahhat: Software, Data curation, Writing–original draft. All authors read and approved the final manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research and Libraries in Princess Nourah bint Abdulrahman University for funding this research work through the Research Group project, Grant No. (RG-1445-0011).
Acknowledgments
The authors would like to express thank to the Editor-in-Chief and anonymous referees for their constructive comments and suggestions. The authors extend their appreciation to the Deanship of Scientific Research and Libraries in Princess Nourah bint Abdulrahman University for funding this research work through the Research Group project, Grant No. (RG-1445-0011). We would like to thank Wejdan Alajlan for her careful reading of the paper and constructive suggestions for improving its results.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: