Analyzing the dynamics of fractional spatio-temporal $\mathrm{SEIR}$ epidemic model

1.   Introduction

The history of infectious diseases has witnessed various epidemics, causing significant global health problems. The World Health Organization (WHO) indicates that infectious diseases cause the death of more than 17 million people annually ^[1,2]. Experimental challenges in epidemiology, exacerbated by underreporting and the infeasibility of conducting experiments, require the use of mathematical modeling and numerical simulation ^[3]. Since 1760 ^[4], the pioneering work of Daniel Bernoulli demonstrated that mathematical models (MMs) are useful tools in understanding the spread of infectious diseases. Subsequent literature, including Roland Ross's study of malaria dynamics ^[5] and the classic SIR epidemic model proposed by Kermack and McKendrick in 1927 ^[6], laid the foundation for modeling disease transmission. In the context of recent global challenges, such as COVID-19 pandemic, the use of MMs has proven essential to estimate parameters that have a significant influence on disease behavior, help to understand disease dynamics and guide public health interventions. Answering all the following questions about the persistence or elimination of the epidemic, its duration, its impact on population density, and finally, how to control it requires considering spatial factors ^[7,8]. The SEIR model was introduced to account for asymptomatic infected individuals (such as SARS, tuberculosis, and flu), i.e., the exposed individuals $\mathrm{E}$. In fact, the SEIR model is more suitable for diseases that have a latent period, such as influenza A(H1N1), measles, and AIDS ^[9,10]. Those SEIR models are governed by a system of ODEs, where they focus only on the temporal variable $t$. However, it is clearly evident that the infection propagation is affected not only by time but also by spatial variables, denoted as $x$ ^[11,12,13]. This effect of spatial dynamics plays a pivotal role in saturated incidence rates, influencing effective contacts between $\mathrm{I}$ and $\mathrm{S}$. In general, introducing spatial variables as diffusion terms enhances the realism of the modeling, as demonstrated in ^[14]. Researchers have tried to inculcate spatial aspects by delving into reaction-diffusion models, such as the generalized reaction-diffusion rumor propagation model based on a multiplex network ^[15], the spatio-temporal SIR model with diffusion that describes the transmission of diseases (e.g., whooping cough) ^[16,17], and the asymptotic analysis of the SIR model with reaction-diffusion operator and linear source ^[18].

Fractional derivatives (FDs), which are non-integer derivatives, have become essential in MMs where the state depends on its history due to the hereditary and memory effects accompanied by the FDs. These properties are useful in modeling infectious diseases and other ecological models. In addition, the FDs possess a higher degree of freedom than the classic derivative, allowing for a more accurate and suitable description of the proposed FOM's dynamics. Therefore, the MMs involving the FDs have been observed in diverse fields such as modeling the infectious diseases ^{[19,20,21,22]}, mechanics ^[23], physical systems ^[24,25], control theory ^[26,27,28], biology ^[29,30], viscoelasticity ^[31], and engineering ^[32]. Of this overview, the major features of FOMs can be summarized as follows: Anomalous diffusion phenomena, innate memory effects, fractal capture, better data fit, and multi-scale nature. Furthermore, FOMs provide a powerful tool for integrating the impact of memory and the hereditary features of the infectious disease models compared to their integer-order counterparts, where these features cannot be displayed because they do not have non-local interactions. The study of fractional calculus (FC) has gained popularity, leading to more definitions of FDs with some additional advantages and properties ^[33,34,35], but the Caputo and Riemann–Liouville FDs are the most popular ^[36,37]. MMs within FDs have gained prominence in describing disease progression, providing enhanced precision compared to classical derivatives ^[38]. Generally, the discontinuous nature of disease spread, not well-described by ODEs, is effectively captured by FOMs ^[39]. Modeling epidemics within FDEs greatly benefits from the use of Caputo FD ^[36,40]. This inclusion in MMs allows for a more accurate and realistic analysis of infectious disease dynamics. Moreover, due to extensive human mobility within a country or even worldwide, models that assume spatial uniformity are insufficient to describe disease spread accurately. More precisely, the advantages of using fractional PDEs than fractional ODEs to characterize the $\mathrm{SEIR}$ model are that it enables the incorporation of spatial variables and realistic disease transmission patterns. The spatial approach found in fractional PDEs enhances the accuracy and realism of the dynamic of epidemiological models, making fractional PDEs a valuable tool for understanding the spread and elimination of infectious diseases. For this reason, spatial effects of $\mathrm{S}, \; \mathrm{E}, \; \mathrm{I},$ and $\mathrm{R}$ must be taken into account to understand the spread of epidemics comprehensively. Motivated by the discussion mentioned above, we introduce the following FOM:

subject to the following positive initial conditions (ICs):

where $_{0}^{C}\!\mathfrak{D}_{t}^{\alpha}$ is Caputo fractional partial derivative (CFPD) of order $\alpha \in(0, 1]$ and $\mho$ is bounded set in $\mathbb{R}^{2}$ with smooth boundary $\partial\mho$. For the biologically feasible region, we mean that the total population remains within the studied domain and this leads us to the following no-flux homogeneous Neumann boundary conditions (BCs):

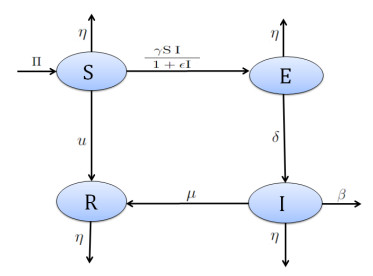
where $n$, $\partial_{n} = \frac{\partial }{\partial n} = n. \nabla$ represent the outward unit normal vector on $\partial \mho$ and the normal derivative, respectively. The following diagram illustrates the dynamics of the FOM (1.1) that we proposed (see Figure 1).

The total population $\mathrm{N}(t, x)$ is comprised of the following compartments: $\mathrm{S}(t, x), \; \mathrm{E}(t, x), \; \mathrm{I}(t, x)$ and $\mathrm{R}(t, x)$, which denote susceptible, exposed, infected, removed individuals at spatial location $x$, and time $t$, respectively. The positive constants $d_{\mathrm{S}}, \; d_{\mathrm{E}}, \; d_{\mathrm{I}}$, and $d_{\mathrm{R}}$ denote the corresponding diffusion rates for $\mathrm{S}, \; \mathrm{E}, \; \mathrm{I}$, and $\mathrm{R}$, respectively. It assumed that susceptible individuals are recruited at rate $\Pi$, $\eta$ is the natural death rate, $\delta$ is the transmission rate from $\mathrm{E}(t, x)$ to $\mathrm{I}(t, x)$, $\mu$ is the human recovery rate and $\beta$ is the disease mortality rate. The vaccination rate per unit of time is denoted by $u$ and $\Delta$ represents the Laplacian operator. Several authors have recommended the saturation rate as an important factor in modeling epidemic dynamics ^[41,42,43]. In ^[6], the bilinear incidence rate ($g(\mathrm{I})\mathrm{S} = \gamma \mathrm{S} \mathrm{I}$, where $g$ is the incidence function and $\gamma$ is the transmission rate) is incorporated with the classical SIR epidemic model. This simpler saturation form of the infection have been utilized in many works to model infectious diseases, see e.g., ^[44,45] and references therein. It is more suitable for communicable diseases like influenza etc., but not for sexually transmitted diseases. In 1973, Capasso and Serio ^[46] proposed a generalization of previous incidence by introducing a saturated incidence rate ($g(\mathrm{I})\mathrm{S} = \gamma\mathrm{S}\mathrm{I}/(1 +\epsilon \mathrm{I}$), $\epsilon$ is the human saturation constant of $\mathrm{I}$) into epidemic models, where considered to be of Michaelis–Menten form ^[47] and $g(I)$ tends to a saturation level when $\mathrm{I}$ gets large. This incidence rate is more reasonable than the bilinear incidence rate ($\gamma \mathrm{S} \mathrm{I}$) because it takes into account the behavioral change and crowding effect of infected individuals. It also prevents the transmission rate from being unbounded by choosing appropriate parameters ^[48,49].

The primary contribution of our work is to provide a comprehensive analysis of the $\mathrm{SEIR}$ epidemic model of fractional order that is characterized by a saturated incidence function. Through a system of PDEs within CFPD, the FOM integrates the $\mathrm{E}(t, x)$ component and spatial diffusion, which enhances its realism in tracking the behavior of disease dynamics. We determine the suitability of FOM, performs the stability analysis of all possible EPs as well as computes $\mathcal{R}_{0}$, and explores the influence of changing $\alpha$ on the model dynamics. The sensitivity analysis of FOM shows which parameters have a significant impact on $\mathcal{R}_{0}$. Numerical simulations demonstrate the validity of our theoretical results and emphasize the critical role of vaccination in mitigating the severity of infection. The proposed FOM is a valuable tool for understanding and predicting the spatio-temporal transmission dynamics of SEIR, with a suggestion to apply control strategies and guide public health interventions. Finally, one of the most important recommendations we reached in this work is to integrate the time FDs into infectious disease models in order to examine disease dynamics before reaching equilibrium states.

This work is organized as follows: Section 2 is dedicated to outlining some fundamental definitions and theorems for FC that lay the groundwork for our subsequent analysis. In Subsection 3.1, we examine the existence, boundedness, and positivity of the projected solution, which are crucial aspects for understanding the dynamics of our model. In Subsection 3.2, we focus on investigating the stability of all possible EPs in order to provide insight into the projected solution behavior, and Subsection 3.3 is devoted to discussing the results of sensitivity analysis of FOM parameters. In Section 4, graphical simulations of the numerical solutions are displayed. Concluding remarks are given in Section 5.

2.   Preliminaries

Now, we recall the definitions of CFPD, Laplace transform (LT) and Mittag–Leffler function (see, e.g., ^[50,51,52]).

Definition 2.1. For a function $g(t) \in L^{1}(\mathbb{R}^{+})$, the Riemann-Liouville fractional integral is expressed as:

Definition 2.2. For a function $g(x, t) \in AC^{n}([0, +\infty), \mathbb{R}^{+})$, the CFPD of order $\alpha$ is defined as follows:

Definition 2.3. Let $G(s)$ be the LT of the function $g(t)$. Then, the LT of CFPD is given by the following formula ^[51]:

where $\alpha \in (n-1, n]; \; n \in \mathbb{N}$.

Definition 2.4. The two-parameter Mittag-Leffler function $\mathcal{M}_{a, b}(x)$ is defined as

We now introduce the following properties of $\mathcal{M}_{a, b}(x)$ ^[50]:

Proposition 2.1. (Green formula ^[52]) Let $D$ be a domain of $\mathbb{R}^{n}$ and $\nu(x)$ its exterior normal, then Green formula for the two regular functions $v$ and $w$ is given by

where $\partial D$ is the boundary of region $D$.

We now state the following definition of the Lyapunov function and some lemmas ^{[53,54,55,56,57]} in order to prove the stability of EPs.

Definition 2.5. Let $\Theta(\Xi)$ be a neighborhood of $\Xi$, then the real-valued differentiable function $\mathcal{V}$ defined on $\Theta(\Xi)$ is said to be the Lyapunov function for (1.1) if

$(1) \; \mathcal{V}(\Xi) = 0$; and

$(2) \; \mathcal{V}(\Xi_{1}) > 0$ in $\Theta(\Xi), \; \forall\; \Xi\neq \Xi_{1}$.

Lemma 2.1. Let $\Omega$ be a positively invariant subset of $\Pi$ where $\Pi\subseteq \mathbb{R}^{n}$ and the function $y:\Pi \rightarrow \mathbb{R}$ is continuously differentiable such that $y(x) > 0$, $^{C}\!\mathfrak{D}^{\alpha}_{t}y(x(t))\leq0$ in $\Omega$ for the solutions $x(t)$. Suppose the set $\digamma$ contains all points in $\Omega$ where $^{C}\!\mathfrak{D}^{\alpha}_{t}y(x(t)) = 0$ and $\Sigma$ is the largest invariant set in $\digamma$. Then, every bounded solution starting in $\Omega\rightarrow \Sigma$ as $t \rightarrow \infty$.

Lemma 2.2. Let $y(t)\in \mathbb{R}^{+}$ be a continuous differentiable function. Then, $\forall \; t \geq 0$ and $\alpha \in (0, 1)$

where $\Phi(y) = (y-1-\ln(y))\geq 0$ for any $\; y > 0$.

3.   Qualitative analysis of model dynamics

Here, we examine the behavior of the proposed FOM (1.1) in order to understand its general characteristics. These analyses allow us to establish the theory of positivity and boundedness of the solutions. Moreover, it helps us describe solution trends by evaluating EPs, investigating the stability of these EPs and demonstrating the results of sensitivity analysis states.

3.1.   Existence, positivity, and boundedness of solutions

We now begin our analysis by stating the positivity and boundedness theorem to ensure that the projected solutions of FOM (1.1) reflect biological reality. Letting $X = C(\bar{\mho}, \mathbb{R})$ be a Banach space equipped with usual norms. The system (1.1)–(1.2) can be rewritten as:

where $\lambda = (\mathrm{S}, \mathrm{E}, \mathrm{I}, \mathrm{R})^{T}$, the initial values $\lambda_{0} = (\mathrm{S}_{0}, \mathrm{E}_{0}, \mathrm{I}_{0}, \mathrm{R}_{0})^{T}$, $A\lambda(t, x) = (d_{\mathrm{S}} \Delta \mathrm{S}, d_{\mathrm{E}} \Delta \mathrm{E}, d_{\mathrm{I}} \Delta \mathrm{I}, d_{\mathrm{R}} \Delta \mathrm{R})^{T}$ such that $A:D(A)\subset X^{4} \longrightarrow X^{4}$ is linear diffusion operator with $D(A) = \{ \lambda \in X^{4}: \Delta \lambda \in X^{4}, \; \dfrac{\partial \lambda}{\partial n} = 0_{\mathbb{R}^{4}_{+}}\; \text{for}\; x \in \partial \mho\}$ and the function $F:[0, T]\times X^{4} \longrightarrow X^{4}$ defined as

Theorem 3.1. The problem (3.1) has a unique positive solution for all $\alpha \in (0, 1]$.

Proof. Obviously, $A$ is an operator from a dense set $D(A)$ into itself and $F$ is Lipschitz continuous in $X$. Following Theorem 3.1 in ^[58], the unique non-negative solution of the FOM (1.1)–(1.2) can be achieved. □

Theorem 3.2. The solution of FOM (1.1) is bounded on $\mho \times [0, +\infty)\; \; \forall \; t\geq 0$.

Proof. In order to show boundedness of the solution, we write the total number of population as the following equation:

We now add Eq (1.1) and integrate both sides of the result over $\mho$. Thus, we have

According to Green's formula (2.4) and applying BCs (1.3), then

From Eq (3.2) with the linear property of CFPD, we get

Taking LT of the above equation as follows:

Then, we have

Using Eq (2.2), Eq (2.3) and the positivity of ICs, we obtain

where $K = \max \bigg\{\dfrac{\Pi}{\eta}, \mathrm{N}(0)\bigg\}$. From Theorem 3.1 and Eq (3.3), we conclude that $0\leq N(t, x)\leq \frac{\Pi}{\eta}$, which means that the solution is positive and bounded. Hence, our proposed FOM (1.1) is meaningful both mathematically and epidemiologically. □

3.2.   Local and global stability of EPs

Certainly, in the mathematical modeling of infectious diseases, evaluating EPs, $\mathcal{R}_{0}$, investigating local and global stability, and discussing sensitivity analysis of FOM parameters are important tools for analyzing such diseases. These analyses allow a good understanding of how such diseases spread and develop in a population. We begin by evaluating EPs that provide insights into the behavioral dynamics of an outbreak, as well as calculating $\mathcal{R}_{0}$ as a key threshold for predicting the spread of disease ($\mathcal{R}_{0} > 1$) or die out ($\mathcal{R}_{0} < 1$), which is essential for public health experts. Now, let $\mathcal{E}$ be the EP of (3.1), then $F(\mathcal{E}) = 0$,

Thus,

Before proceeding to determine the EPs, we introduce the following lemma.

Lemma 3.1. ^[59] The EP $\mathcal{E}$ for the system (3.1) is local asymptotically stable (LAS) if all eigenvalues $\lambda_{i}\; (i = 1, 2, ..., n)$ of the Jacobian matrix (JM) at $\mathcal{E}$ satisfy $|\mathit{\text{arg}}(\lambda_{i})| > \frac{\alpha \pi}{2}$.

Figure 2 shows the stability region of a fractional order system (where $\Im(\lambda)$ and $\Re(\lambda)$ represent the imaginary and real parts of the eigenvalues, respectively). By observing this figure, the advantages of fractional order models are that such systems have wider stability margins and can accurately detect the behavior of many phenomena.

By solving Eq (3.5), we get the following two EPs.

● A disease-free equilibrium (DFE) point ($\underline{\mathrm{I} = 0 }$): There is no infection $\Xi_{f} = (\mathrm{S}_{f}, \mathrm{E}_{f}, \mathrm{I}_{f}, \mathrm{R}_{f}) = \bigg(\dfrac{\Pi}{\eta+u}, 0, 0, \dfrac{u\Pi}{\eta (\eta+u)}\bigg)$. Using NGM method ^[60], the BRN can be given by $\rho(\mathcal{F}\mathcal{V}^{-1})$ where $\rho$ is the spectral radius, $\mathcal{F}$ and $\mathcal{V}^{-1}$ are defined as follows:

Hence, the BRN is expressed as

Next, we establish the theorems of local and global stability of $\Xi_{f}$ based on the expression of BRN (3.6) and using the following subsystem:

with the general Jacobian matrix (JM) of Eq (3.7) at $\Xi_{eq} = (\mathrm{S}_{eq}, \mathrm{E}_{eq}, \mathrm{I}_{eq}, \mathrm{R}_{eq})$:

Theorem 3.3. Whenever $\mathcal{R}_{0} < 1$, then the DFE $\Xi_{f}$ is LAS and unstable if $\mathcal{R}_{0} > 1$.

Proof. At $\Xi_{f}$ the JM Eq (3.8) becomes

The eigenvalues for $J_{\Xi_{f}}$ are

This shows that $\chi_{2} < 0, \; \chi_{3} < 0$ whenever $\mathcal{R}_{0} < 1$. Hence, the DFE ${\Xi_{f}}$ for the FOM (1.1) is LAS. However, if $\mathcal{R}_{0} > 1$, it becomes unstable. □

Theorem 3.4. Whenever $\mathcal{R}_{0} < 1$, then the DFE $\Xi_{f}$ is globally asymptotically stable (GAS).

Proof. Suppose the positive Lyapunov function has the following form

where $k_{1} = \eta+\delta$. Calculating the CFPD of $\mathcal{V}_{1}$ with Lemma 2.2 and substituting from Eq (3.7), we get

Applying formula (2.4) and BCs (1.3) with $\Pi = (\eta+u)\mathrm{S}_{f}$, we can write

Now, we observe that:

- If $\mathcal{R}_{0}\leq 1$, then $_{0}^{C}\!\mathfrak{D}_{t}^{\alpha}\mathcal{V}_{1}(t, x)\leq 0$.

- If $_{0}^{C}\!\mathfrak{D}_{t}^{\alpha}\mathcal{V}_{1}(t, x) = 0$, then $\mathrm{S} = \mathrm{S}_{f}$ and $\mathcal{R}_{0}-1-\epsilon \mathrm{I} = 0$, $\mathrm{I} = 0, \; \mathrm{E} = 0$, whenever $\mathcal{R}_{0} = 1$.

As a result, $\{ (\mathrm{S}, \mathrm{E}, \mathrm{I})\in \mathbb{R}^{3}_{+}: \; _{0}^{C}\!\mathcal{D}_{t}^{\alpha}\mathcal{V}_{1}(t, x) = 0\} = \{ \Xi_{f}\}$ and by using fractional LIP (Lemma 2.1), then the EP $\Xi_{f}$ is LAS. □

● An endemic equilibrium (EE) point ($\underline{\mathrm{I}\neq 0 }$): Here, the disease persists among the population. Let $\Xi^{*} = (\mathrm{S}^{*}, \mathrm{E}^{*}, \mathrm{I}^{*}, \mathrm{R}^{*})$ represents EE point and from Eq (3.5)

Then we can summarize the results of the existence of $\Xi_{f}$ and $\Xi^{*}$ as follows:

Theorem 3.5. The DFE $\Xi_{f}$ always exists, and the unique positive EE $\Xi^{*}$ exists whenever $\mathcal{R}_{0} > 1$.

Finally, in this subsection, we clarify the local and global stability of $\Xi^{*}$.

Theorem 3.6. The unique positive point $\Xi^{*}$ (3.10) is LAS if $\mathcal{R}_{0} > 1$.

Proof. The JM of Eq (3.7) corresponding to $\Xi^{*}$ (3.10) is given by

where $Q_{1} = \eta+u+\dfrac{\gamma \mathrm{I}^{*}}{1+\epsilon \mathrm{I}^{*}}$, $Q_{2} = \dfrac{\gamma \mathrm{S}^{*}}{(1+\epsilon \mathrm{I}^{*})^{2}}$. Then, the characteristic polynomial of the matrix $J_{\Xi^{*}}$ is

with the coefficients $\mathcal{A}_{i}; \; i = 0, 1, 2$

Hence, $\mathcal{A}_{1}, \; \mathcal{A}_{0}$ are positive values if $\mathcal{ R}_{0} > 1$, this implies that the eigenvalues $\omega_{j}\; (j = 1, 2, 3)$ of Eq (3.12) have negative real parts, and using the condition stated in Lemma 3.1, i.e., $|\mbox{arg}(\omega_{j})| > \frac{\alpha \pi}{2}$ for each $j = 1, 2, 3$, then EE point $\Xi^{*}$ is LAS. □

Theorem 3.7. The EE point $\Xi^{*}$ (3.10) is GAS if $\mathcal{R}_{0} > 1$.

Proof. Assuming the Lyapunov function as follows:

Using Lemma 2.2 and from Eq (1.1), we have

Applying formula (2.4) with BCs (1.3) and using $\Pi = (\eta+u) \mathrm{S}^{*}+(\eta+\delta)\mathrm{E}^{*}, \; \dfrac{\mathrm{E}^{*}}{\mathrm{I}^{*}} = \dfrac{\eta+\mu+\beta}{\delta}$, then

From Eq (3.4), we have $\dfrac{\gamma \mathrm{S}^{*} \mathrm{I}}{1+\epsilon \mathrm{I}} = (\eta+\delta) \mathrm{E}^{*} \dfrac{\mathrm{I}}{\mathrm{I}^{*}}$, then

where, for example $\bigg[-2+\dfrac{\mathrm{S}}{\mathrm{S}^{*}}+\dfrac{\mathrm{S}^{*}}{\mathrm{S}}\bigg] = \bigg[\dfrac{\mathrm{S}}{\mathrm{S}^{*}}-1-\ln\bigg(\dfrac{\mathrm{S}}{\mathrm{S}^{*}}\bigg)+\dfrac{\mathrm{S}^{*}}{\mathrm{S}}-1-\ln\bigg(\dfrac{\mathrm{S}^{*}}{\mathrm{S}}\bigg)\bigg]\geq 0$, from the definition of function $\Phi$ in Lemma 2.2. Therefore, $_{0}^{C}\!\mathfrak{D}_{t}^{\alpha}\mathcal{V}_{2}(t, x)\leq 0$ and if $_{0}^{C}\!\mathfrak{D}_{t}^{\alpha}\mathcal{V}_{2}(t, x) = 0$, then $\mathrm{S} = \mathrm{S}^{*}, \; \mathrm{E} = \mathrm{E}^{*}$ and $\mathrm{I} = \mathrm{I}^{*}$. This means that $\{ (\mathrm{S}, \mathrm{E}, \mathrm{I}) \in \mathbb{R}^{3}_{+}:\; _{0}^{C}\!\mathfrak{D}_{t}^{\alpha}\mathcal{V}_{2}(t, x) = 0\}$ is singleton set $\{\Xi^{*}\}$ and from fractional LIP (Lemma 2.1), whenever $\mathcal{R}_{0} > 1$, then $\Xi^{*}$ is GAS. □

3.3.   Sensitivity analysis of FOM parameters

Here, we investigate the sensitivity analysis of the FOM (1.1) parameters. The initial disease transmission is directly related to BRN. Therefore, a sensitivity analysis will be performed on $\mathcal{R}_{0}$ to find the parameters that have a high effect on disease transmission. Following Chitnis et al. ^[61], the forward sensitivity index formula is given by:

where $\Upsilon_{p}^{\mathcal{R}_{0}}$ is the sensitivity index of $\mathcal{R}_{0}$ in relation to parameter $p$. For instance, the sensitivity index for parameters $\eta$, $u$, and $\delta$ are given as follows:

For other parameters in $\mathcal{R}_{0}$ (3.6), the sensitivity indices of $\mathcal{R}_{0}$ and their parameter values are shown in Figure 3a. From Figure 3a, b, we note that the value of BRN increases with the increase of $\Upsilon_{p}^{\mathcal{R}_{0}}$ with a positive sign, while this value decreases with the increase of $\Upsilon_{p}^{\mathcal{R}_{0}}$ with a negative sign.

From the above results of sensitivity analysis, we observe that the most sensitive parameters are $\eta, \Pi, \gamma, \delta$, and so on (see Figure 3a). Figure 3b shows the effect of $u$ on $\mathcal{R}_{0}$ and $\Upsilon_{u}^{\mathcal{R}_{0}}$, which means that the most effective way in order to control disease transmission is to provide more vaccinations so that $\mathcal{R}_{0}$ less than one.

4.   Numerical results and discussion

In this section, we illustrate the outcomes of our numerical simulations that aim to validate the theoretical findings discussed in Section 3. The fractional order system (1.1)–(1.3) is integrated numerically by applying the centered and forward finite difference approaches in order to discretize the diffusion operator and CFPD, respectively ^[62,63], as follows: let $\mho = [0, L]$ and $h_{t} = \frac{T}{N}$ and $h_{x} = \frac{L}{n}$ be the times and space time step, respectively, $t_{i} = i h_{t}$ for $i = 0, 1, ..., N$ and $x_{j} = j h_{x}$ for $j = 0, 1, ..., n$. This approach gives an accuracy of order $(2-\alpha)$ in time and order 2 in space ^[64]. For simplicity, we denote the approximate solutions of $\mathrm{S}(t_{i}, x_{j}), \mathrm{E}(t_{i}, x_{j}), \mathrm{I}(t_{i}, x_{j}), \mathrm{R}(t_{i}, x_{j})$ by $\mathrm{S}_{j}^{i}, \mathrm{E}_{j}^{i}, \mathrm{I}_{j}^{i}$ and $\mathrm{R}_{j}^{i}$, respectively. We can write, for example, the approximation of $\; _{0}^{C}\!\mathfrak{D}_{t}^{\alpha}\mathrm{S}(t_{i}, x_{j})$ and $\Delta \mathrm{S}(t_{i}, x_{j})$, respectively, as follows:

and

The same applies to the other compartments $\mathrm{E}(t_{i}, x_{j}), \mathrm{I}(t_{i}, x_{j})$ and $\mathrm{R}(t_{i}, x_{j})$. Then, we have the following scheme for the FOM (1.1):

In the following numerical simulations, the model parameter values are given in Table 1 ^[65,66], with these ICs $\mathrm{S}_{0} = 10, \; \mathrm{E}_{0} = 20, \; \mathrm{I}_{0} = 20$, and $\mathrm{R}_{0} = 30$. We use the one-dimensional interval $0 \leq x \leq L$, $0 \leq t \leq T$, and $d_{\mathrm{S}} = d_{\mathrm{E}} = d_{\mathrm{I}} = d_{\mathrm{R}} = 0.2$ (km per day).

Now we focus on the behavior of obtained solutions related to the stability of $\Xi_{f}$, $\Xi^{*}$ and the effect of changing $\alpha, \; \epsilon$ and $u$ as follows: Figure 4 shows the dynamics of $\mathrm{S}, \; \mathrm{E}, \; \mathrm{I}$, and $\mathrm{R}$, in which case the disease will become extinct (where $\mathcal{R}_{0} = 0.001748 < < 1$) within the period of infection. The main observation from Figure 4a, b is that the solutions converge towards the DFE point $\Xi_{f}$. This is consistent with Theorem 3.4, which illustrates that $\Xi_{f}$ is GAS. Moreover, the dynamics of $\mathrm{S}, \; \mathrm{E}, \; \mathrm{I}$, and $\mathrm{R}$ for the parameters corresponding to the second row in Table 1 are determined in Figures 5 and 6. These parameters, give $\mathcal{R}_{0} = 12.107 > 1$ (where $u = 0$), $\mathcal{R}_{0} = 0.9313 < 1$ (where $u = 0.6$), and we observe from Figures 5 and 6 the tendency of the solutions towards convergence to the endemic equilibrium. Therefore, according to Theorem 3.7, the EE point $\Xi^{*}$ is GAS, and the disease will persist in the population (see Figure 5), while Figure 6 displays the impact of vaccination on the behavior of solutions and how their states change based on the value of $u$. From Figures 7a and 8a, we can observe the effect of $\alpha$ on the behavior dynamics of $\mathrm{S}, \; \mathrm{E}, \; \mathrm{I}$ and $\mathrm{R}$. Moreover, for low values of $\alpha$ indicative of a "long memory effect", the solutions converge more rapidly toward the steady state (see, e.g., dash-dotted line ($\alpha = 0.7$) and dotted line ($\alpha = 0.5$)). Consequently, we deduce from this numerical experiment that the Caputo fractional operator solely affects the speed of convergence toward the steady states.

Therefore, it is recommended to incorporate FDs into infectious disease models in order to examine disease dynamics before reaching equilibrium states. Figures 7b and 8b show the influence of saturated infection rate $\epsilon$ on the dynamics of $\mathrm{S}, \; \mathrm{E}, \; \mathrm{I}$, and $\mathrm{R}$. For the DFE $\Xi_{f}$, it is evident from Figure 7b that variations in the values of $\epsilon$ have a very slight effect on $\mathrm{E}, \; \mathrm{I}$, and $\mathrm{R}$, while their effect is clearly shown on $\mathrm{S}$. On the other hand, for EE $\Xi^{*}$, increasing in the values of $\epsilon$ leads to a decrease in the number of $\mathrm{E}$ and $\mathrm{I}$, as well as an increase in the number of $\mathrm{S}$ and $\mathrm{R}$ as shown in Figure 8b.

As a result, we deduce that maintaining a high value for $\epsilon$ is crucial for controlling disease spread. Figures 7c and 8c show the impact of changing the vaccination rate $u$ on the behavior of $\mathrm{S}, \; \mathrm{E}, \; \mathrm{I}$, and $\mathrm{R}$. It is evident that as the vaccine concentration increases, the number of $\mathrm{I}$ decreases dramatically, and the number of $\mathrm{R}$ increases to a maximum at the expense of $\mathrm{S}$, especially concerning the EE (see Figure 8c). Finally, in Figure 9, the extent of the influence of $u$ on $\mathcal{R}_{0}$ is evident, where $u$ ranges from 0 (no vaccination) to 1 (high rate of $u$). We consider only the case of EE for $\alpha = 0.9$ in which $\mathcal{R}_{0}$ decreases with increasing $u$, as depicted in Figure 9. This highlights the crucial role of vaccination in reducing infections.

5.   Conclusions

In this study, we analyze the spatio-temporal SEIR epidemic model, described by a system of PDEs involving CFPD and featuring diffusion operators for its components $\mathrm{S}, \; \mathrm{E}, \; \mathrm{I}$ and $\mathrm{R}$. The incorporation of the exposed component $\mathrm{E}(t, x)$ and spatial propagation $\Delta$ (Laplacian operator) alongside the CFPD enhances the realism of the model in tracking disease dynamics. The existence, uniqueness, positivity, and boundedness of the solutions are demonstrated, ensuring the suitability of the proposed FOM. Furthermore, the spreading behavior of the disease has been elucidated by evaluation of all EPs and establishing their local and global stability theorems based on BRN and Lyapunov functions. A sensitivity analysis of the proposed FOM has been conducted to identify the parameters that have a significant effect on $\mathcal{R}_{0}$ and lead to outbreaks of infection in the population. Additionally, numerical simulations have been presented to illustrate the theoretical results and show the importance of vaccination strategies in reducing the severity of infection. The proposed FOM has not only contributed to stability analysis but also provided insights into disease evolution as well as, in some cases, influenced the time required to reach stable states "memory effects" (as has been reported in Figures 7a and 8a). In future work, we can include the vaccination term $u$ in an optimal control problem within Caputo FD or other FDs having non-singular kernels.

Author contributions

All authors of this article have been contributed equally. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to thank the Deanship of Scientific Research at Majmaah University for supporting this work under project no. R-2024-1320.

Conflict of interest

The authors declare no conflicts of interest in this paper.