Longitudinal PLS-SEM analysis of the performance and participation of students in mathematics

1.   Introduction

The mathematics literacy scores collected by the Programme for International Student Assessment ^[1] for Year 9 students in Australia were the worst since 2000. Australia's 33-point decline in average scores for mathematical literacy between 2003 and 2018 was the one of the worst out of 41 members of the Organization for Economic Cooperation and Development (OECD). The average mathematics literacy score placed Australia 27th in the league table of OECD countries. The PISA scores are not the only index of the plummeting mathematical performance of Australia's students. Mathematics performance has also declined according to independent data collected by the National Assessment Program – Literacy and Numeracy (NAPLAN) and the Trends in International Mathematics and Science Study (TIMSS). This chronic decline is of serious concern to the Australian Government ^[2].

Australia does not force high school students to study mathematics after Year 9 before graduation in Year 12. Since 2001, Australian students have been permitted to drop out of mathematics after Year 9. The proportions of students choosing to participate in mathematics subjects after Year 9 has decreased continuously since 2001, especially among girls. Between 2001 and 2014, the proportions of eligible students studying mathematics fell from 100% in 2001 to 90.7% among boys and to 78.6% among girls. Only 29.6% of Year 12 students in Australia participated in high-level mathematics in 2018, representing a significant loss for the Australian economy in terms of the professional capabilities and quantitative skills needed in the future ^[3]. Wilson ^[4] asserted that Australia is in a precarious position in the world's competitive knowledge economy because so many high school students are dropping out of mathematics after Year 9, even among those who intend to pursue University degrees in science, engineering, technology, science, and mathematics (STEM). Australia's STEM Workforce warned that if Australian students continue to be outperformed by their international counterparts, then the nation risks a future without essential population-wide specialized mathematical skills ^[5].

According to Prieto and Dugar ^[6], the development of negative perceptions toward mathematics in the K-12 curriculum among Australian students can be attributed to several factors identified in their study. The author highlights that a significant portion of students (approximately 55%) reported mathematics is not useful in everyday life, which is compounded by the perception that mathematics is overly difficult and abstract. Kennedy ^[7] suggested that students' self-perceptions regarding their weak abilities in mathematics, as well as their misconceptions about the perceived usefulness and difficulty of mathematics, were possible reasons for the continuous decline in mathematics participation in Australian schools. Kim ^[8] argued that the decline in high school students' acquisition and development of skills in mathematics explains the concomitant drop in the numbers of students who subsequently take up STEM courses and careers. Prieto and Dugar ^[6] highlighted that a significant portion of students (approximately 62%) reported that mathematics is not important in their future career. Furthermore, Prieto and Dugar ^[6] found that 50% of students felt that what they have learned so far will be useful in their future career. These insights provide a clearer understanding of the underlying reasons for the negative attitudes toward mathematics observed in Australian students. Thus, we hypothesized that six non-cognitive factors controlled or explained the relationship between mathematics performance in Year 9 and the subsequent mathematics participation of the same students in Year 12, specifically: gender and five self-related beliefs: mathematics self-concept, self-efficacy, interest, motivation, and anxiety.

We hypothesized that gender moderated (i.e., controlled) the strength and direction of the correlation between mathematical performance in Year 9 and subsequent mathematics participation in Year 12. This hypothesis is supported by the well-known gender gap in mathematics performance among high school students ^[9,10,11,12]. Huang et al. ^[13] concluded that gender has a strong moderating effect on the correlations between mathematics self-efficacy and interest in mathematics. Van Mier et al. ^[14] reported that gender differences moderate the relationship between mathematics anxiety and mathematics performance. Boys may be more motivated than girls to achieve higher test scores in mathematics because boys believe that mathematical skills may ultimately result in better job prospects and a higher income ^[15].

Based on previous research, we hypothesized that five non-cognitive factors related to the self-related beliefs of high school students mediated (i.e., explained) the correlation between mathematics performance in Year 9 and mathematics participation in Year 12. Van der Beek et al. ^[16] reported that self-concept mediates the correlation between mathematics performance and the enjoyment of mathematics. Grigg et al. ^[17] found that self-efficacy was positively correlated with mathematics performance. Prast et al. ^[18] concluded that the motivation of students to participate in mathematics subjects was positively correlated with their previous academic performance, while the perceived competence of students in mathematics (i.e., their self-efficacy) was a strong predictor of their subsequent achievements in mathematics. The high level of anxiety felt by many high school students who experience learning difficulties in mathematics is a significant predictor of their poor mathematics performance ^[19,20]. Palestro and Jameson ^[21] concluded that mathematics self-efficacy mediates the correlation between mathematics anxiety and mathematics performance. Habók et al. ^[22] found that motivation and other self-related beliefs predicted the mathematics performance of high school students. Recber et al. ^[19] concluded that self-efficacy, anxiety, motivation, gender, and type of school predicted test scores in mathematics. Silinskas and Kikas et al. ^[23] identified longitudinal correlations between the mathematics performance of 3^rd to 6^th-grade students and their levels of motivation, defined as a combination of task persistence and self-concept. Özcan and Kültür ^[24] reported that a high level of mathematics self-efficacy, associated with mastery experience, was a significant predictor of a high level of mathematics performance in high school seniors.

Although other researchers have analyzed and interpreted the mathematics performance of Year 9 Australian students using PISA test scores ^[2,3,4,5,25], little is known about the factors that may intervene in the relationship between previous mathematics test scores and subsequent mathematics participation. Consequently, we contribute to a gap in the literature by addressing research questions beginning with "how much" that embrace "what else is known" and take "how uncertain" into consideration ^[26].

The overarching question is: Among one cohort of Australian students, how much is the correlation between the mathematics performance in Year 9 and the subsequent mathematics participation in Year 12 related to the gender and the self-belief factors of the students in Year 9? The following three sub-questions were addressed:

RQ1: How much does the mathematics performance of the students in Year 9 predict the same students' level of participation in mathematics subjects in Year 12?

RQ2: How much is the level of participation in mathematics subjects in Year 12 moderated by the gender of the students?

RQ3: How much is the correlation between the mathematics performance of the students in Year 9 and the same students' level of participation in mathematics subjects in Year 12 mediated by: (a) mathematics self-efficacy; (b) mathematics self-concept; (c) mathematics anxiety; (d) interest in mathematics; and (e) motivation in mathematics.

2.   Materials and methods

The data utilized in this study is from the Longitudinal Surveys of Australian Youth (LSAY) dataset. The demographic characteristics of the LSAY study sample are based on one cohort of Australian students, with a total of N = 7145 participants, who were part of the LSAY beginning in 2007. LSAY, an initiative by the Australian Government Department of Education, tracks young Australians over a period of 10 years. This cohort includes individuals transitioning from their mid-teens to mid-twenties, providing data as they progress through secondary education, higher education, and into the workforce. The LSAY data aims to capture a comprehensive view of the educational and occupational pathways of Australian youth, facilitating an understanding of the factors influencing their development and career trajectories ^[27].

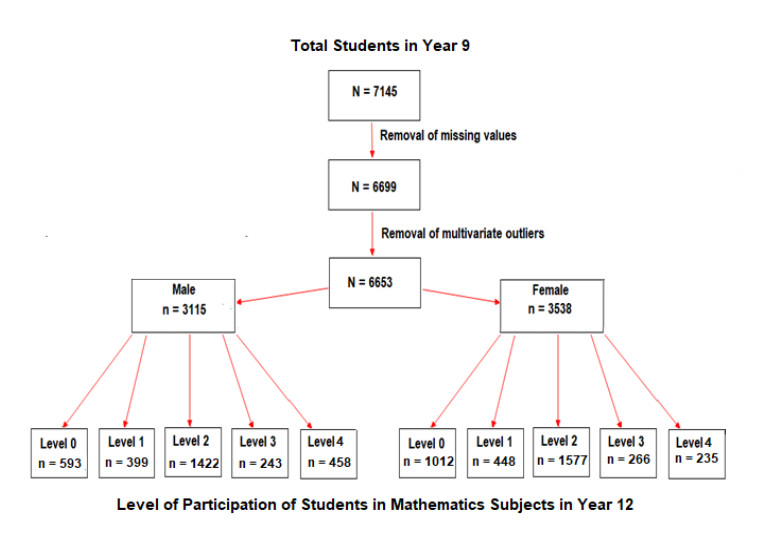
The sampling tree in Figure 1 illustrates that, after removal of missing values and multivariate outliers (identified by Mahalanobis D²), the proportion of male students among the remaining N = 6653 students (n = 3115, 46.8%) in the LSAY was less than the proportion of female students (n = 3538, 53.2%). The proportion of female students who did not participate in mathematics subjects (Level 0) in Year 12 (n = 1012, 28.6%) was over twice the proportion of male students in Level 0 (n = 593, 19.0%). Most of the male students (n = 2522, 81.0%) participated in mathematics subjects at either Level 1, 2, 3, or 4 in Year 12; while a smaller proportion of the female students (n = 2526, 71.4%) participated in mathematics subjects in Year 12 at Level 1, 2, 3, or 4. The variables measured by LSAY are defined in Table 1. Six non-cognitive variables were hypothesized to moderate (i.e., control) or mediate (i.e., explain) the positive correlation between the mathematics performance of Austrian students in Year 9 (i.e., the predictor) and their subsequent mathematics participation in Year 12 (i.e., the outcome). The strengths and directions of the relationships between the predictor, non-cognitive factors, and the outcome were explored by partial least squares structural equation modeling (PLS-SEM) using SmartPLS software v.2. The process of estimating the mediating and moderating effects followed the protocols defined by ^[28].

Figure 1.  Sampling tree.

DownLoad: Full-Size Img PowerPoint

Table 1.  Definitions of variables.

Variable name		Conceptual definition	Functional definition	Operational definition
Mathematics participation in Year 12	MATPAR	Participation of Australian students in mathematics subjects in Year 12	Outcome	Five ordinal categories: 0 = No participation; 1 = Level 1; 2 = Level 2; 3 = Level 3; 4 = Level 4 Higher levels reflect greater participation in mathematics subjects.
Mathematics performance in Year 9	MATPER	Australian students' level of literacy and knowledge in mathematics subjects in Year 9. Questionnaire components derived from context-rich situations covering four dimensions of mathematics: quantity, shape and space, change and relationship, and uncertainty	Predictor	Average score for 106 items with constructed response or multiple-choice formats. Each score was transformed to a standardized scale for OECD states, ranging from 300 to 800. Higher scores reflect better performance.
Mathematics self-efficacy in Year 9	MATSEF	Self-efficacy in mathematics refers to a student's belief in their ability to succeed in mathematical tasks and apply mathematical concepts in real-life situations. Australian students' ratings in Year 9 about their capacity to excel in mathematics and their ability to apply mathematical concepts in real-life situations. 1: Using a train timetable; 2: Calculating a 30-percent discount; 3: Calculating m2 of tiles needed to cover a floor. 4: Understanding graphs. 5: Solving an equation; 6: Finding the distance between two places on a map; 7. Solving an equation. 8: Calculating the petrol consumption rate of a car.	Mediator	Linear combination of ordinal scores for 8 items each measured with a 4-point Likert scale: 0 = Not at all confident; 1 = Not very confidence; 3 = Confident; 4 = Very confident. Higher scores reflect greater levels of self-efficacy.
Mathematics self-concept in Year 9	MATSLC	Self-concept in mathematics refers to a student's perception of their abilities and competence in the subject. It is a multifaceted construct that influences motivation, engagement, and performance in mathematics. Australian students' ratings in Year 9 about their ability to study mathematics. 1: I am just not good at mathematics. 2: I get good marks in mathematics. 3: I learn mathematics quickly. 4: I have always believed that mathematics is one of my best subjects. 5: In my mathematics class, I understand even the most difficult work.	Mediator	Linear combination of ordinal scores for 5 items each measured with a 4-point Likert scale: 0 = Strongly agree; 1 = Agree; 2 = Disagree; 3 = Strongly disagree. Higher scores reflect greater levels of self-concept.
Interest in mathematics in Year 9	INTMAT	How much each Australian student in Year 9 expressed interest in mathematics. 1: I enjoy studying mathematics. 2: I look forward to my mathematics lessons. 3: I do mathematics because I enjoy it. 4: I am interested in the things I learn in mathematics.	Mediator	Linear combination of ordinal scores for 4 items each measured with a 4-point Likert scale: 0 = Strongly disagree; 1 = Disagree; 2 = Agree; 3 = Strongly agree. Higher scores reflect greater levels of interest.
Motivation in mathematics in Year 9	MOTMAT	How much Australian students in Year 9 were motivated to study mathematics. 1: Making an effort in mathematics is worth it because it will help me in the work that I want to do later on. 2: Learning mathematics is worthwhile for me because it will improve my career prospects, chances. 3: Mathematics is an important subject for me because I need it for what I want to study later on. 4: I will learn many things in mathematics that will help me get a job.	Mediator	Linear combination of ordinal scores for 4 items each measured with a 4-point Likert scale: 0 = Strongly disagree; 1 = Disagree; 2 = Agree; 3 = Strongly agree. Higher scores reflect greater levels of motivation.
Mathematics anxiety in Year 9	MATANX	How much Australian students in Year 9 felt anxiety to study mathematics. 1: I often worry that it will be difficult for me in mathematics classes. 2: I get very tense when I do mathematics homework. 3: I get very nervous doing mathematics problems. 4: I feel helpless when doing a mathematics problem. 5: I worry that I will get poor marks in mathematics.	Mediator	Linear combination of ordinal scores for 4 items: 0 = Strongly disagree; 1 = Disagree; 2 = Agree; 3 = Strongly agree. Higher scores reflect greater levels of anxiety.
Gender	GENDER	Sex of student	Moderator	Two nominal categories: 0 = Male; 1 = Female

---

 | Show Table

DownLoad: CSV

The path diagram in Figure 2 displays a hypothetical generalized model of the relationship between the mathematics standardized test scores of the students in Year 9 (scaled from 225 to 833) and their subsequent level of mathematics participation in Year 12 (scaled from 0 to 4). The standardized regression coefficients (ß) representing the point estimates of the partial correlations were defined by ß₁ = the direct effect of mathematics performance in Year 9 (MATPER) on mathematics participation in Year 12 (MATPAR); ß₂ x ß₃ = the indirect effect of MATPER on MATPAR mediated by a non-cognitive self-belief factor (i.e., mathematics self-concept, self-efficacy, interest, mathematics motivation, or mathematics anxiety); ß₄ = the partial correlation between the moderator (gender coded by 0 = male; 1 = female) and MATPAR; and ß₅ = the moderating effect of gender on MATPAR, estimated as the product of gender x MATPAR.

Figure 2.  Path diagram of the generalized model.

DownLoad: Full-Size Img PowerPoint

The statistical significance of the ß coefficients based on a threshold p-value was not reported, because "it is illogical and inappropriate to declare the results to be either significant or not significant" ^[29]. Moreover, "p-values below 0.05 do not prove the reality of anything. Nor, come to that, do p-values above 0.05 disprove anything" ^[30]. Over 800 scientists in over 50 countries have agreed that "it is time for statistical significance to go" and "we must learn to embrace uncertainty" ^[31].

Bootstrapping with 1000 random samples using the Monte Carlo algorithm provided a normalized estimate of each ß coefficient, and its level of uncertainty, reflected by the standard error (SE) and 95% confidence interval (CI = ß ± 1.96 SE). The benchmarks to interpret effect sizes in the context of social science followed the criteria recommended by Ferguson ^[32] supported by the American Psychological Association. The strengths of the path coefficients were indicated by ß = 0.2 as the "recommended minimum effect size representing a practically significant effect (RMPE)", while ß = 0.5 represents a "moderate effect" and ß = 0.64 is a "strong effect". The overall effect size was indicated by the coefficient of determination (R²) reflecting the proportion of the variance in mathematics participation explained by the model. R² = 4% represents the RMPE, R² = 25% is a "moderate effect", and R² = 64% is a "strong effect" ^[32].

Practical significance (reflected by ß > 0.2 and R² > 0.04) refers only to the "impressiveness" of the results; however, standardized benchmarks do not necessarily reflect the "relevance" or "real-world usefulness" of the results ^[33]. The interpretation of effect sizes in educational research depends on many confounding factors, including the research design and context, the sample size, the validity and reliability of the measures, and the robustness of the chosen statistical model ^[34,35,36].

An evaluation of the quality criteria of the models constructed by PLS-SEM used the method recommended by Hair et al. ^[29] and justified the interpretation of effect-size benchmarks. The sample size (N = 6663) provided a high level of statistical power (99%) to identify practically significant effects. The factorial validity of the reflective latent variables measured as linear combinations of ordinal scores (see Table 1) was good. The loading coefficients were consistently strong (λ ≥ 0.5) for all indicators used to operationalize each latent variable (see Table 2). The average variance explained (AVE) in each latent variable was consistently ≥ 50% (see Table 3). The internal consistency reliabilities were excellent (composite reliability coefficient = 0.84 to 0.91, see Table 3). The discriminant validity of the operationalized latent variables was also good (HTMT ≤ 0.85), because their loading coefficients were consistently greater than the cross-loadings on alternative variables (see Table 4). The models constructed using PLS-SEM did not violate the theoretical assumption that the predictor, mediator, and moderator variables should not be strongly multicollinear, indicated by small variance inflation factors (VIF = 1.33 to 3.28).

Table 2.  Loadings coefficient.

	MOTMAT	MATANX	MATSEF	MATSLC	INTMAT
IM1					0.841
IM2					0.871
IM3					0.918
IM4					0.864
IMM1	0.863
IMM2	0.896
IMM3	0.882
IMM4	0.808
MAN1		0.789
MAN2		0.795
MAN3		0.780
MAN4		0.796
MAN5		0.689
MSC1				0.838
MSC2				0.815
MSC3				0.854
MSC4				0.849
MSC5				0.817
MSE1			0.589
MSE2			0.747
MSE3			0.782
MSE4			0.685
MSE5			0.728
MSE6			0.741
MSE7			0.717
MSE8			0.651

---

 | Show Table

DownLoad: CSV

Table 3.  Construct reliability and validity.

	Cronbach's alpha	Composite reliability (rho_a)	Composite reliability (rho_c)	Average variance extracted (AVE)
MOTMAT	0.887	0.913	0.921	0.745
MATANX	0.829	0.840	0.880	0.594
MATSEF	0.857	0.866	0.888	0.500
MATSLC	0.891	0.895	0.920	0.697
INTMAT	0.896	0.901	0.928	0.764

---

 | Show Table

DownLoad: CSV

Table 4.  Discriminant validity: HTMT.

	MOTMAT	MATANX	MATPAR	MATPER	MATSEF	MATSLC	INTMAT
MOTMAT
MATANX	0.316
MATPAR	0.318	0.372
MATPER	0.176	0.406	0.430
MATSEF	0.403	0.569	0.439	0.603
MATSLC	0.504	0.834	0.460	0.451	0.676
INTMAT	0.615	0.528	0.394	0.216	0.483	0.724

---

 | Show Table

DownLoad: CSV

3.   Results

RQ1: Direct effect of mathematics performance → mathematics participation

The first set of PLS-SEM results in Table 5 indicate that, in the absence of gender and self-belief factors, the moderate positive path coefficient ß = 0.430 [0.379, 0.490] indicated that a high level of mathematics performance in Year 9 predicted a correspondingly high level of mathematics participation in Year 12. The effect size was substantially greater than the RMPE: R² = 0.184 [0.167, 0.201]. The conclusion was that the simple direct effect of mathematics performance on subsequent mathematics participation in the absence of moderators and mediators was practically significant and relevant in the context of the research.

Table 5.  Direct effect of mathematics performance → mathematics participation.

Effect	ß	95% CI
MATPER → MATPAR	0.430	0.379, 0.490
Note. R2 = 0.184 [95% CI = 0.167, 0.201].

---

 | Show Table

DownLoad: CSV

RQ2: Moderating effect of gender

The second set of PLS-SEM statistics in Table 6 indicate that the addition of gender as a moderator increased the proportion of the variance explained in the relationship between mathematics performance and mathematics participation compared to the first model; R² = 0.196 [0.178, 0.212]. The moderating effect of gender was indicated by a negative path coefficient: ß = -0.235 [-0.386, -0.084]. The negative coefficient implied that the strength of the relationship between mathematics performance → mathematics participation decreased when the students were female (coded by 1) compared to when the students were male (coded by 0). The reason for this interaction was that the mean scores for mathematics performance of the male students at each level of participation from 0 to 4 (M = 505.90 to 643.93) were consistently greater than the mathematics performance of the female students at each level of participation from 0 to 4 (M = 500.03 to 6522.68]. The conclusion is that the gender of the students had a small but practically significant moderating effect on the prediction of the mathematics participation of the students in Year 12.

Table 6.  Moderating effect of gender on mathematics performance → mathematics participation.

Effect		ß	95% CI
MATPER → MATPAR	ß1	0.457	0.424, 0.490
GENDER → MATPAR	ß4	0.136	0.001, 0.271
Moderating effect	ß5	-0.235	-0.386, -0.084
Note. R2 = 0.196 [95% CI = 0.178, 0.212].

---

 | Show Table

DownLoad: CSV

RQ3: Mediating effects of self-belief factors and moderating effect of gender

The PLS-SEM statistics in Table 7 combine the mediating effects of the five self-belief factors with the moderating effects of gender. All of the ß coefficients were above the RMPE (>0.2) reflecting the practical significance of the partial correlations. The lower and upper limits of the 95% CI of R² captured 0.25, and were consistently greater than zero, reflecting the moderate levels of practical significance of the models. The direct effects of mathematics performance on mathematics participation (ß = 0.282 to 0.403) were less than the direct effect in the absence of mediation and moderation in the first model (ß = 0.430). This reduction in the direct effect reflected partial mediation by the self-belief factors, and explained the proportion of the variance in mathematics participation that was not explained by mathematics performance.

Table 7.  Mediating effects of self-belief factors and moderating effect of gender on mathematics performance → mathematics participation.

Mediator	Direct effect	Indirect effects		Mediating effect	95% CI Mediating effect	Moderating effect	95% CI Moderating effect	Effect Size	95% CI R2
	ß1	ß2	ß3	ß2 x ß3		ß5		R2
MATSEF	.282	.565	.305	.172	.142, .203	-.269	-.163, -.375	.237	.219, .255
MATSLC	.323	.565	.241	.136	.114, .159	-.233	-.074, -.392	.233	.215, .251
MATANX	.384	-.374	-.202	.076	.051, .100	-.232	-.079, -.385	.229	.211, .247
INTMAT	.403	.206	.291	.060	.035, .085	-.254	-.103, -.405	.276	.258, .294
MOTMAT	.422	.176	.232	.041	.016, .065	-.254	-.401, -.107	.247	.229, .265

---

 | Show Table

DownLoad: CSV

Mathematics self-efficacy, self-concept, interest, and motivation were positively correlated with mathematics performance in Year 9 (ß₁ = 0.282 to 0.422) and with mathematics participation in Year 12 (ß₁ = 0.176 to 0.565). The 95% CI of the ß coefficients did not capture zero, implying that in 95 out of 100 samples, a high level of mathematics self-belief resulted in both a high level of mathematics performance in Year 9 and a high level of mathematics participation in Year 12.

Mathematics anxiety was negatively correlated with mathematics performance in Year 9 (ß₂ = -0.374) and negative correlated with mathematics participation in Year 12 (ß₃ = -0.202). The 95% CI of the two ß coefficients did not capture zero, indicating that in 95 out of 100 samples, a high level of mathematics anxiety resulted in a low level of mathematics performance and participation.

The mediators with the strongest indirect mediating effects on the positive correlation between mathematics performance in Year 9 and mathematics participation in Year 12 were mathematics self-efficacy (ß₂ x ß₃ = 0.172) and mathematics self-concept (ß₂ x ß₃ = 0.136), followed in order of magnitude by mathematics anxiety (ß₂ x ß₃ = 0.076), interest in mathematics, and motivation in mathematics (ß₂ x ß₃ = 0.041). Irrespective of which mediators were included in the model, the strength of the moderating effect of gender was always negative, and had a similar magnitude (ß₅ = -0.233 to -0.269). The strength of the correlation between mathematics performance and participating was consistently stronger for the boys compared to the girls.

4.   Discussion

Statistical evidence with effect sizes reflecting practical significance was provided to address the research questions. Specifically, it was observed that mathematics performance of students in Year 9 contributed about 18.4% in explaining the participation level of students in mathematics in Year 12. Similarly, when the effect of gender was accounted for, mathematics performance of students in Year 9 contributed about 19.6% in explaining the participation level of students in mathematics in Year 12. Also, when the relationship was mediated by self-belief factors, mathematics performance of students in Year 9 contributed between 23%–25% in explaining the participation level of students in mathematics in Year 12.

Furthermore, the mathematics performance of the students in Year 9 predicted the same students' level of participation in mathematics subjects in Year 12. The level of participation in mathematics subjects in Year 12 was moderated by the gender of the students. The correlation between the mathematics performance of the students in Year 9 and the same students' level of participation in mathematics subjects in Year 12 was mediated by: (a) mathematics self-efficacy, (b) mathematics self-concept, (c) mathematics interest, (d) mathematics anxiety, and (e) motivation in mathematics.

For any given level of mathematics performance in Year 9, a male student with a higher level of mathematics self-concept, self-efficacy, interest, and motivation, and a lower level of anxiety, was more likely to participate in mathematics subjects in Year 12 than a female student with a lower level of mathematics self-concept, self-efficacy, interest, and motivation, and a higher level of anxiety. These findings align with the principles of self-determination theory (SDT), which emphasizes the importance of intrinsic motivation and self-efficacy in academic achievement. According to SDT, when students possess a high level of mathematics self-efficacy and interest, their intrinsic motivation is enhanced, leading to reduced mathematics anxiety and increased future participation in mathematics subjects, as supported by ^[17]. Conversely, Moustafa et al. ^[37] found that elevated mathematics anxiety undermines intrinsic motivation, resulting in decreased interest in mathematics. This underscores the SDT perspective that fostering a supportive and confidence-building environment is crucial for enhancing students' intrinsic motivation and interest in mathematics.

The use of PLS-SEM in the current research generated empirical models that were consistent with the models using CB-SEM created by ^[22] based on the 2000 PISA assessment scores at two measurement points. These models showed how non-cognitive self-related beliefs (self-concept, self-efficacy, intrinsic motivation, and interest) functioned as mediators to predict the future mathematics achievement of students in secondary school, and that self-concept had the strongest effect.

The knowledge that mathematics participation in Year 12 can be predicted using mathematics performance in Year 9 has practical applications for administrators, teachers, and policymakers in educational settings. Although the effect sizes of the models constructed in the present study were not strong, the findings have implications with respect to the making of recommendations and policy decisions in educational settings. The reason why so many Australian high school students, especially girls, appear to have developed negative perceptions, associated with poor academic performance and participation in mathematics, could be due to the prevalence of traditional styles of teaching (e.g., memorization and regurgitation of rote procedures) which has limited intellectual and social appeal. To improve the participation of Australian students in mathematics subjects, more teachers should adopt collaborative pedagogic strategies that reinforce students' motivation and non-cognitive skills ^[38]. More students need to understand that investing time and effort into learn mathematics produces beneficial returns ^[22].

The findings of this study reinforce the recommendations of the Australian government ^[2] that teachers need to transform their classrooms into mastery-oriented environments. Australian teachers need to promote increased student interest and reduce learning costs, by applying strategies to improve non-cognitive self-related beliefs, including self-concept, self-efficacy, and intrinsic motivation. School administrators should try to build school cultures that provide the resources to support professional learning and evidenced-based teaching in mathematics.

The knowledge that mathematics participation in Year 12 and mathematics performance in Year 9s mediated by psychological factors and moderated by demographic factors has theoretical implications. In order to achieve better student performance in mathematics, the mastery model is recommended to help reduce mathematics anxiety and improve mathematics self-efficacy ^[39,2]. More social interaction in the classroom, involving collaboration between students, as well as positive socio-emotional support from teachers, should help students to complete tasks, achieve goals, stimulate the growth mindset, and improve the mastery, motivation, self-concept, and self-efficacy in the context of learning mathematics ^[13].

5.   Practical implications

The findings of this study have significant practical implications for educational administrators, teachers, and policymakers. Understanding that mathematics performance in Year 9 can predict mathematics performance and participation in Year 12 emphasizes the importance of early intervention and support. The study showed that non-cognitive factors such as mathematics self-concept, self-efficacy, motivation, and interest mediate this relationship, suggesting that these non-cognitive factors are crucial for sustaining students' engagement in mathematics. Given that gender also plays a role, with male students generally showing higher participation when they have positive self-related beliefs, targeted strategies to boost these beliefs among female students could help close the gender gap in mathematics participation. Therefore, educational policies should promote teaching methods that enhance students' self-efficacy and interest in mathematics, as these are linked to reduced anxiety and increased long-term engagement.

Furthermore, the study's results also support the need for a shift in teaching practices to foster a more mastery-oriented learning environment, as recommended by the Australian government. Traditional teaching methods that focus on rote memorization may contribute to negative perceptions of mathematics and lower participation rates. Instead, adopting collaborative and student-centered pedagogical strategies could improve motivation and non-cognitive skills, making mathematics more appealing. Teachers should focus on creating a supportive classroom atmosphere that boosts students' mathematics self-concept and motivation, thus reducing anxiety and improving overall performance. School administrators play a vital role in providing the necessary resources and professional development opportunities for teachers to implement these evidence-based practices. By doing so, they can help cultivate a positive school culture that prioritizes students' psychological well-being and academic success in mathematics.

6.   Conclusions

This exploratory research has achieved its goal of generating new ideas and questions that may ultimately feed into future research and policies to improve the mathematics performance and participation of high school students in Australia and elsewhere. These findings contribute to a gap in the literature regarding the factors that may predict the participation of students in mathematics after Year 9 in Australia and provide new insights to explain the network of interrelationships between the self-belief factors that mediate the correlation between mathematics performance and participation among high school students. These findings also inform researchers, administrators, and teachers about how they may contribute to the slowing down or stopping of the plummeting performance and participation of Australian students in mathematics.

7.   Limitations and future work

More research using SEM is recommended to explore the effects of additional factors on the positive correlation between mathematics performance in Year 9 and mathematics participation in Year 12. The effects of pedagogic factors (e.g., applying the mastery model and the growth mindset) and social factors (e.g., the level of parental involvement) need to be estimated in order to determine the degree to which they mediate the positive correlation between mathematics performance in Year 9 and mathematics participation in Year 12. The effects of demographic factors (e.g., the socioeconomic status and race/ethnicity of the students) need to be estimated in order to determine the degree to which they moderate the strength and/or direction of the correlation between mathematics performance in Year 9 and mathematics participation in Year 12.

More qualitative research based on the principles of hermeneutical phenomenology in the context of the learning of mathematics may provide richer results to answer deeper questions beginning with "Why" rather than "How much?". For example, Australian high school students could be interviewed individually and asked open-ended questions to provide insight into their lived experiences, such as: "Why do you enjoy/not enjoy mathematics?"; "Why do you look forward/not look forward to your mathematics lessons?"; "Why are you interested/not interested in mathematics?"; "Why do you think learning mathematics will improve/not improve your career?"; "Why do you feel anxious/not anxious about learning mathematics?"; and "Why do you think that you get good marks/poor marks in mathematics?".

In addition, based on the findings and in line with the recommendations of Prieto and Dugar ^[6], future studies should investigate the role of teachers, curriculum design, and instructional methods in fostering mathematical proficiency and interest among students. This research should focus on how different teaching approaches and curriculum structures can enhance students' self-efficacy and intrinsic motivation in mathematics, thereby reducing anxiety and increasing engagement and participation in mathematics subjects. Additionally, exploring the specific practices that successful teachers use to cultivate a positive learning environment could provide valuable insights for improving math education outcomes.

Use of AI tools declaration

The author declares that he has not used artificial intelligence (AI) tools in the creation of this article.

Conflict of interest

The author declares no conflict of interest.