Unification of Adomian decomposition method and ZZ transformation for exploring the dynamics of fractional Kersten-Krasil'shchik coupled KdV-mKdV systems

1.   Introduction

Fractional order Kersten-Krasil'shchik (KK) coupled Korteweg-de Vries (KdV)-modified KdV (mKdV) systems have served as the focus of extensive research in recent years due to their potential use in a variety of disciplines, including fluid dynamics, nonlinear optics and plasma physics ^[1,2,3,4]. These systems are characterized by the presence of fractional derivatives, which introduce non-local and memory effects into the dynamics of the system ^[5,6,7,8]. The KK coupled KdV-mKdV system is a system of two coupled nonlinear partial differential equations, which describe the evolution of two waves in a dispersive medium. The first equation is the well-known KdV equation, which describes the propagation of small amplitude, long wavelength waves. The second equation is the mKdV equation, which describes the propagation of larger amplitude, shorter wavelength waves. The KK coupling term, which is a nonlinear and non-local term, describes the interaction between the two waves ^[3,4,7]. Li et al. delved into an epidemic model's analysis and comparisons with other mechanisms in 2018 ^[12], while Jin and Wang explored chemotaxis phenomena in 2016 ^[13]. He et al. focused on fixed-point and variational inequality problems for Hadamard manifolds in 2022 ^[14]; this was followed by He et al. discussing nonexpansive mapping algorithms in 2023 ^[15]. Chen et al. contributed to particle physics, discovering hidden-charm pentaquarks in 2021 ^[16]. Lyu et al. analyzed cavity dynamics in water entries ^[17], whereas Yang and Kai delved into nonlinear Schr$\ddot{o}$dinger equations in 2023.

Time fractional Kersten-Krasil'shchik coupled KdV-mKdV nonlinear system and homogeneous two component time fractional coupled third order KdV systems are very important fractional nonlinear systems for describing the behaviour of waves in multi-component plasma and elaborate various nonlinear phenomena in plasma physics. Other studies have focused on the stability, existence and uniqueness of solutions for KK coupled KdV-mKdV systems of fractional order. In addition to these studies, there have been many other works that have explored the properties of fractional order KK coupled KdV-mKdV systems, such as their integrability, conservation laws and soliton interactions. Overall, the literature on fractional order KK coupled KdV-mKdV systems is rich and diverse, and it continues to grow as researchers explore new properties and applications of these systems ^[18,19,20].

There are several methods that have been proposed to solve the fractional KdV (fKdV) equation and the mKdV equation. One of these methods is the homotopy perturbation method; this method uses a perturbation series and a homotopy approach to solve nonlinear differential equations. It has been used to find approximate solutions to the fKdV equation ^[21]. The variational iteration method uses a variation of a trial solution to find approximate solutions to nonlinear differential equations. The homotopy analysis method uses a homotopy approach and a perturbation series to solve nonlinear differential equations. It has been used to find approximate solutions to the fKdV equation ^[22] and the mKdV equation ^[23]. The Adomian decomposition method uses a decomposition of the nonlinear term of a differential equation into a series of simpler functions. It has been used to find approximate solutions to the fKdV equation and the mKdV equation ^[24,25]. Yang and Kai, dynamical properties, modulation instability analysis and chaotic behaviors to the nonlinear coupled Schrodinger equation in fiber Bragg gratings ^[26]. Chen et al. presented a linear free energy relationship in chemistry in 2020 ^[27]. Luo et al. proposed a new gradient method for force identification in vehicle-bridge systems in 2022 ^[28]. Additionally, Chen et al. focused on adaptive control of underwater vehicles in 2022 ^[29]. Lastly, Gu, Li and Liao developed an evolutionary multitasking approach for solving nonlinear equation systems in 2024 ^[30]. These studies collectively offer significant insights and advancements across a broad spectrum of scientific research areas, enriching our understanding and methodologies in their respective domains.

The ADM is a powerful technique for solving nonlinear differential equations. Developed by George Adomian in the late 1980s, the ADM is based on the idea of decomposing the solution of a nonlinear equation into a series of simpler functions, known as Adomian polynomials. These polynomials are obtained by iteratively applying the nonlinear operator to a constant function ^[31,32]. The ADM has been applied to a wide range of nonlinear problems, including partial differential equations, integral equations and stochastic differential equations. One of the key advantages of the ADM is its ability to handle equations with singularities, such as those that arise in physics and engineering. In recent years, researchers have been exploring the use of the ADM in combination with other techniques, such as the ZZ transform. The ZZ transform is a mathematical tool that can be used to transform a nonlinear equation into a linear equation, making it easier to solve. By combining the ADM with the ZZ transform, researchers have been able to solve a wide range of nonlinear problems with greater efficiency and accuracy. Many researchers have used the ADM together with the ZZ transform to solve, for example, the nonlinear fractional partial differential equations in fluid dynamics, nonlinear integral equations in quantum mechanics and nonlinear fractional stochastic differential equations in finance. Overall, the ADM with the ZZ transform has been shown to be an efficient and flexible strategy for addressing nonlinear problems, with numerous potential applications in various fields ^[33,34].

The current work is organized as follows. In Section 2, some fundamental definitions of fractional calculus are provided. The basic ideas of the Aboodh transform and the ADM are described in Section 3. In Section 4, we build approximate solutions to fractional Kersten-Krasil'shchik coupled KdV-mKdV systems of partial differential equations. Section 5 contains the conclusions.

2.   Preliminaries

Definition 2.1. For functions, the Aboodh transformation is achieved as follow:

which is described as follows ^[33,34]:

Theorem 2.2. Consider $G$ and $F$ as the Aboodh and Laplace transformations, respectively, of $\textit U(\varrho)$ over the set $B$ ^[35,36]. Then

Generalizing the Laplace and Aboodh integral transformations, Zain Ul Abadin Zafar created the ZZ transformation ^[37]. The ZZ transform is described as follows.

Definition 2.3. For all values of $\varrho \geq 0$, the Z-transform for the function $\textit U(\varrho)$ is $Z(\kappa, \varepsilon)$, which can be expressed as follows ^[37]:

The Z-transform is linear in nature, just as the Laplace and Aboodh transforms. On the other hand, the Mittag-Leffler function (MLF) is an expansion of the exponential function:

Definition 2.4. The Atangana-Baleanu-Caputo (ABC) derivative of a function ${U}(\varphi, \varrho)$ in the space $H^{1}(a, b)$ for ${{\beta}} \in \; (0, 1)$ has the following definition ^[38]:

Definition 2.5. The Atangana-Baleanu Riemann-Liouville (ABR) derivative is a part of the space $H^{1}(a, b)$. The derivative can be represented for any value of ${{\beta}} \in (0, 1)$ as follows ^[38]:

The property of the function ${B}({{\beta}})$ is that it tends to 1 for both 0 and 1. Additionally, $\forall \; {{\beta}} > 0$, ${B}({{\beta}}) > {a}$.

Theorem 2.6. The Laplace transformation for the ABR derivative and ABC derivative are given by ^[38]:

and

In the theorems below we assume that ${U}({\varrho}) \in H^{1}(a, b)$, where $b > a$ and ${{\beta}} \in (0, 1)$.

Theorem 2.7. The Aboodh transform gives rise to a new ABR derivative, which is known as the Aboodh transformed ABR derivative ^[36]

Theorem 2.8. The Aboodh transformation of ABC derivative is defined as follows ^[36]:

Theorem 2.9. The $\mathrm{ZZ}$ transformation of ${U}({\varrho}) = {\varrho}^{{{\beta}}-1}$ is defined as

Proof. The Aboodh transformation of ${U}({\varrho}) = {\varrho}^{{{\beta}}}, \ \ {{\beta}} \geq 0$ is given by

Applying Eq (2.6), we obtain

□

Theorem 2.10. Let ${{\beta}}$ and $\omega$ be complex numbers and assume that the real part of ${{\beta}}$ is greater than 0. The $\mathrm{ZZ}$ transformation of $E_{{{\beta}}}\left(\omega {\varrho}^{{{\beta}}}\right)$ can be defined as follows ^[36]:

Proof. The Aboodh transformation of $E_{{{\beta}}}\left(\omega {\varrho}^{{{\beta}}}\right)$ is defined as follows:

So,

we obtain

□

Theorem 2.11. The ZZ transform of the ABC derivative can be defined as follows: If $G({\varepsilon})$ and $Z({\kappa}, {\varepsilon})$ are the ZZ and Aboodh transformations of ${U}({\varrho})$, respectively ^[36], they we have

Proof. Applying this Eqs (2.1) and (2.5), we get

The ABC $Z$ transformation is represented as follows:

□

Theorem 2.12. Let us assume that the ZZ transformation of ${U}({\varrho})$ is represented by $G({\varepsilon})$ and the Aboodh transformation of ${U}({\varrho})$ is represented by $Z({\kappa}, {\varepsilon})$. Then, the ZZ transformation of the ABR derivative is defined as ^[36]

Proof. Applying Eqs (2.1) and (2.4), we get

□

3.   General methodology of ADM within ZZ transformation

In this section, we will examine the equation known as the fractional partial differential equation:

with the initial condition

where $\mathcal{L}(\varphi, \wp)$ represents linear terms, ${N}(\varphi, \wp)$ represents nonlinear terms and $h(\varphi, \wp)$ represents the source term.

Using the ZZ transform and ABC fractional derivatives, Eq (3.1) can be re-expressed as follows:

with

By taking the inverse ZZ transform, we get

In terms of Adomain decomposition, we have

The solution to Eq (3.1) can be expressed by using $ADM_{ABC}$.

4.   Numerical result

Example 4.1. Let us examine the following fractional KK joined KdV-mKdV nonlinear system:

with the initial conditions given by

By taking the ZZ transform, we get

Thus we have

By simplification we get

By taking the inverse ZZ transformation, we have

Assume that for the unknown functions $U(\varphi, \wp)$ and $V(\varphi, \wp)$, the series form solution is given as

The nonlinear components of the Adomian polynomials can be represented as follows: $-6U U_{\varphi} + 3V V_{3{\varphi}} = \sum_{m = 0}^{\infty}\mathcal{A}_m$, $3V_{\varphi} V_{2{\varphi}} - 3U_{\varphi} V^{2} = \sum_{m = 0}^{\infty}\mathcal{B}_m$, $6U V V_{\varphi} = \sum_{m = 0}^{\infty}\mathcal{C}_m$ and $-3V^{2}V_{\varphi} - 3U V_{\varphi} + 3U_{\varphi} V = \sum_{m = 0}^{\infty}\mathcal{D}_m$. With the help of these terms, Eq (4.6) can be expressed as follows:

On comparing both sides of Eq (4.8), we have

In this manner, the terms $U{{l}}$ and $V{{l}}$ for $({l}\geq3)$ can be easily obtained. As a result, the series solution can be expressed as follows:

When ${\beta} = 1$, we get the exact solution as

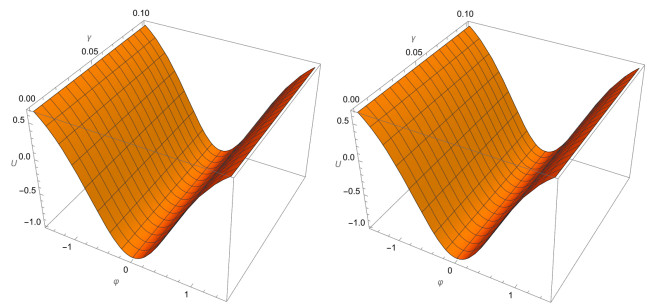
The graphical discussion involves several key figures illustrate the solutions for $U({\varphi}, {\wp})$ and $V({\varphi}, {\wp})$ in Example 4.1 at different parameter values. Figure 1 showcases the analytical and exact solutions at ${\beta} = 1$ for $U({\varphi}, {\wp})$. In Figure 2, the approximate solutions are depicted at ${\beta} = 0.8, 0.6$.

Figure 3 extends the analysis by presenting analytical solutions at various values of ${\beta}$ for $U({\varphi}, {\wp})$. Moving on to $V({\varphi}, {\wp})$, Figure 4 exhibits the analytical and exact solutions at ${\beta} = 1$, while Figure 5 displays the analytical results at ${\beta} = 0.8, 0.6$.

Lastly, Figure 6 provides a comprehensive overview, presenting analytical results at various values of ${\beta}$, including ${\beta} = 1, 0.8, 0.6, 0.4$, for $V({\varphi}, {\wp})$. These figures collectively offer a detailed visual representation of the solutions under different conditions, facilitating a thorough understanding of the system's behavior.

Example 4.2. Let us examine a homogeneous two-component KdV system of third order with a time-fractional component, as follows:

with the initial conditions given by

By taking the ZZ transform, we get

Thus we have

By simplification we get

By taking the inverse ZZ transform, we have

Assume that for the unknown functions $U(\varphi, \wp)$ and $V(\varphi, \wp)$, the series form solution is given as

The representation of nonlinear components using Adomian polynomials is shown as follows: $-UU_{\varphi}-VV_{\varphi} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ and $UV{\varphi} = \sum_{m = 0}^{\infty}\mathcal{B}_m$. With these terms, Eq (4.18) can be expressed as follows:

On comparing both sides of Eq (4.20), we have

By using this method, the terms $U{{l}}$ and $V{{l}}$ can be easily obtained for ${l}\geq3$. Therefore, the solution in the form of a series is as follows:

When ${\beta} = 1$, we get the exact solution as

The graphical discussion involves several key figures that illustrate the solutions for $U({\varphi}, {\wp})$ and $V({\varphi}, {\wp})$ in Example 4.2 at different parameter values. Figure 7 showcases the analytical and exact solutions at ${\beta} = 1$ for $U({\varphi}, {\wp})$. In Figure 8, the approximate solutions are depicted at ${\beta} = 0.8, 0.6$.

Figure 9 extends the analysis by presenting analytical solutions at various values of ${\beta}$ for $U({\varphi}, {\wp})$. We will moving on to $V({\varphi}, {\wp})$.

Figure 10 exhibits analytical and exact solutions at ${\beta} = 1$, while Figure 11 displays the analytical results at ${\beta} = 0.8, 0.6$. Lastly, Figure 12 provides a comprehensive overview, presenting the analytical results at various values of ${\beta}$, including ${\beta} = 1, 0.8, 0.6, 0.4$, for $V({\varphi}, {\wp})$. These figures collectively offer a detailed visual representation of the solutions under different conditions, facilitating a thorough understanding of the system's behavior.

5.   Conclusions

In summary, the combination of the ADM and the ZZ transform has demonstrated its effectiveness in the analysis of the fractional KK coupled KdV-mKdV system encountered in multi-component plasmas. The utilization of this method has yielded accurate and efficient solutions, offering valuable insights into the intricate behavior of these complex systems. Additionally, the incorporation of the ZZ transform has enabled this frequency domain analysis, contributing supplementary information regarding the system's dynamics. This integrated approach stands as a valuable tool for comprehending multi-component plasma behaviors, and it holds the potential for application to analogous systems in future investigations. Future work may explore extending this methodology to different plasma models or investigating the impact of additional physical parameters, thereby broadening the scope of its applicability.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Funding

This work was supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 5081).

Acknowledgments

This work was supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 5081).

Conflict of interest

The authors declare that they have no competing interests.