Orientable vertex transitive embeddings of ${{\sf K}}_p$

1.   Introduction

Population dynamics is one of the subjects that scholars discuss the most. Based on the Lotka-Volterra system, numerous theoretical studies have been developed and applied in various fields ^{[1,2,3,4,5,6]}. The behavior of both predators and prey significantly impacts the dynamics of their populations in a predator-prey system. The use of mathematical models to predict the behavior of predators and prey is of great significance, and scientists can use this as a basis to adopt new strategies to protect species. The predator-prey model is crucial for characterizing the long term evolution of both populations with certain behavior, and its importance can be seen through a large number of models. There are models established based on different theories such as ordinary differential equation ^[7], delay differential equation ^[8], partial differential equation ^[9], stochastic ^[10], cross-diffusion ^[11], reaction-diffusion ^[12], and difference equation, as well as models describing different functional responses such as Holling type ^[10], Holling-Tanner ^[12], ratio-dependence ^[13], Beddington-DeAngelis ^[7], Leslie-Gower ^[14], and Crowley-Martin. There are also models that depict certain behavior such as fear, cooperation, refuge ^[15], herd ^[8], solitary, and social ^[9,16].

All animals in nature need to pay attention to predators even those at the top of the food chain are no exception. Even plants can evade predation through direct or indirect reactions. Fear is a very powerful evolutionary force. Research in ^[17] has shown that using an electrical fence to prevent direct predation of prey can reduce their breeding rates by over $40\%$ throughout an entire breeding season. Similar studies on other species of birds and vertebrates produced consistent results ^[18,19,20]. All of these real experiments indicate that the appearance of predators can lead to a decrease in the number of prey. Scholars have analyzed various models with the fear effect.

The authors in ^[21] proposed a model that modifies the Lotka-Vloterra predator-prey model by incorporating a factor related to fear into the birth rate of the prey:

They showed that the fear effect did not impact system dynamics when predators exhibited a linear response. However, they demonstrated that considering predators with the Holling-Ⅱ response and the fear factor $f(s, y) = \frac{1}{1+sy}$ under certain conditions can stabilize the entire system. The authors also performed numerical simulations on different forms of expression of fear factors and obtained similar results.

Afterward, scholars primarily utilized the first fear factor mentioned above to study various predator-prey models. Recently, Zhu et al. proposed a model ^[22] where the predator is omnivorous and exhibits a linear response:

The dynamics of this system are significantly different from the situation without omnivorous predators. One notable development is the emergence of a new boundary equilibrium point, which is globally asymptotically stable under certain conditions (allowing predators to survive without prey). The second point is that when a positive equilibrium point exists, it is globally asymptotically stable. The third point is that the fear effect can lead to species extinction. Finally, the authors also noted that as the level of fear increases, the population density of predators and prey decreases.

Scholars have studied predator-prey models with fear effects by incorporating other species' behaviors. The authors in ^[23] examined a modified Leslie-Gower predator-prey model in which predators present cooperative hunting behavior. They concluded that the inclusion of a fear factor makes the model more robust than cooperative hunting alone. Sasmal in ^[24] introduced a strong Allee effect in the predator-prey model by incorporating a fear factor. They believed that fear does not have an impact on the dynamics of the positive equilibrium point. They also pointed out that the density of predators decreases as the strength of fear increases. Using the idea presented in ^[25], Lai et al. ^[26] studied the additive Allee effect rather than the multiplicative Allee effect. According to their findings, the multiplicative Allee effect results in less complex dynamics than the additive Allee effect. In ^[27], the authors also researched a model that combines the fear effect and prey refuge. More relevant work can be found in ^[28,29,30].

The fundamental idea of all the studies on predator-prey models relevant to the fear effect discussed above is that the perceived danger of predators by the prey only lowers the birth and survival rate of their offspring, while ignoring the influence on the mature prey's mortality rate. Nevertheless, researchers in ^[17,31,32] believe that the diversity of the food web or long-term physiological consequences may cause the fear effect to raise the death rate of mature prey. In the dangerous natural world, animals that are not at the top of the food chain must remain constantly vigilant against the threat of being preyed upon by native predators; even the smallest mistake could cost them their lives. These bottom-of-the-food-chain species have developed various anti-predator strategies to increase their chances of survival due to their historical fear of predators. However, this anti-predatory behavior can often be detrimental to specialized predators. Predators typically cooperate in the process of predation to facilitate their development.

Experiments have confirmed that fear can reduce the birth and death rates of the prey. Current studies of predator-prey models of the fear effect have been conducted under the assumption that fear reduces the intrinsic growth rate of the prey. We believe that if fear simultaneously reduces the birth and death rates of the prey, the intrinsic growth rate of the prey may be a more complex function of the fear factor, or even a positive function of the fear factor. It is therefore reasonable to consider the effects of fear on the birth and death rates of the prey separately, something that no academic has yet done. In this article, we aim to discuss the dynamics of the model we have proposed. The model combines fear factor and cooperative hunting, particularly emphasizing the fear factor, which not only reduces the birth rate of the prey but also increases their mortality rate. As this is our first attempt at this work, the first issue we need to address is how to construct realistic functions to describe the impact of fear on birth and mortality rates. The solution to this problem is to use the commonly used fear factor by scholars to describe the impact of fear on mortality rate, and to add an additional term with saturation effect to describe the additional mortality caused by fear. Our model is expressed as

where $x(t)$ and $y(t)$ represent the densities of the prey and predators, respectively. Furthermore, $r$, $a$, and $b$ represent the birth rate, death rate, and density constraint coefficient of the prey, respectively, while $c$ and $e$ indicate per capita searching efficiency and degree of cooperation among predators. Additionally, $n$ and $\varepsilon$ represent the death rate and conversion rate of predators. Like other researchers, we use the term $\frac{1}{1+s_{1}y}$ as a measure of fear to describe its impact on the birth rate, where $s_{1}$ represents the level of fear of the prey towards predators. To illustrate the impact of the fear effect on mortality rate, an additional Holling-Ⅱ type functional response $\frac{s_{2}s_{1}y}{1+s_{1}y}$ has been incorporated to account for the saturation effect, where $s_{2}$ represents the maximum level of impact of fear on mortality rate. The reason for using the Holling-Ⅱ type function to describe the effect of predators on the prey mortality is that we believe that the fear function should be an increasing function of predator density with an upper bound.

Our model is more general. It can include no fear effect ($s_{1} = 0$), fear affecting only the birth rate ($s_{1}\neq0, s_{2} = 0$), and fear affecting both birth and death rates ($s_{1}\neq0, s_{2}\neq0$). The first two cases can be regarded as special cases of the third case, so we will mainly consider the third case here. From uniqueness, it follows that the trajectories in the first quadrant cannot cross into other quadrants. Therefore, it is sufficient to discuss only the trajectories in the first quadrant. We focus on the existence and stability of equilibrium points, as well as the impact of the fear effect and cooperative hunting on the system in Section 2. In Section 3, we discuss the different types of bifurcations in the system. In Section 4, we combine an example to illustrate the possibility of bistability in the system. In Section 5, a brief discussion is provided. The final conclusion section elucidates the impact of our findings on ecology or biology.

2.   Stability analysis

We mainly investigated the impact of the fear on the dynamics of the system when there is no cooperative hunting between predators and when there is cooperative hunting.

2.1.   In the absence of cooperative hunting in the system

It is clear that the system (1.1) allows a equilibrium $E_{0}(0, 0)$. In this situation, the existence of the remaining equilibrium points depends on the intrinsic growth rate ($r-a$) of the prey. There is a boundary equilibrium point $E_{1}(\frac{r-a}{b}, 0)$ if $r-a > 0$, and a unique positive equilibrium point $E^{*}(x^{*}, y^{*})$ if $r-a > \frac{bn}{\varepsilon c}$, where

2.1.1.   Stability of all equilibrium points

Proposition 2.1. The following statements are true.

(i) $E_{0}(0, 0)$ is a globally asymptotically stable node if $r-a < 0$ holds, a saddle if $r-a > 0$ holds, and a saddle-node point if $r = a$ holds;

(ii) $E_{1}(x_{1}, 0)$ is a globally asymptotically stable node if $0 < r-a < \frac{nb}{\varepsilon c}$ holds, a saddle if $r-a > \frac{nb}{\varepsilon c}$ holds, and a saddle-node point if $r-a = \frac{nb}{\varepsilon c}$ holds;

(iii) $E^{*}(x^{*}, y^{*})$ is a globally asymptotically stable node as long as it exists.

Proof. The Jacobian matrix of the system is given as

where

(i) The two eigenvalues of $J(E_{0})$ are $r-a$ and $-n$. Clearly, $E_{0}$ is a saddle if $r-a > 0$ holds, and it is a stable node if $r-a < 0$ holds. If $r = a$, by applying the time transformation $d\tau = -ndx$ and expanding the system into a power series around $E_{0}$, we have

Based on the implicit function theorem, we can conclude from the equation $y-\frac{\varepsilon c}{n}xy = 0$ that there exists only one function $y = \varphi(x)$ satisfying the conditions $\varphi(0) = \varphi'(0) = 0$. By simple calculation, we have $y = \varphi(x)\equiv0$. Substituting this into the first equation of the system (2.2), we get $\frac{dx}{d\tau} = \frac{b}{n}x^{2}$. As a result, according to Theorem 7.1 in ^[33], $E_{0}(0, 0)$ is identified as a saddle-node point.

Because we assume that predators are specialists, it is believed that there cannot be predators if there is no prey. This indicates that the equilibrium point cannot occur on the vertical axis. One can easily demonstrate that as $t$ approaches infinity, $x(t)$ and $y(t)$ converge to zero by applying relevant theories from ^[34]. Therefore, $E_{0}$ is a globally asymptotically stable node, leading to the extinction of both species.

(ii) Through an analysis similar to $E_{0}$, we can easily determine that $E_{1}$ is a saddle if $r-a > \frac{nb}{\varepsilon c}$ holds, and a stable node if $r-a < \frac{nb}{\varepsilon c}$ holds. When $r-a = \frac{nb}{\varepsilon c}$, we can transform $E_{1}$ to the origin by setting $(z, y) = (x-x_{1}, y)$, and expanding the system into a power series as follows:

where $m_{1} = r-a$ and $m_{2} = as_{1}s_{2}+rs_{1}+c$. After a non-degenerate linear transformation

and a time transformation $\tau = -m_{1}t$, the system is reduced to

Based on the implicit function theorem, we know from the equation $u+R(u, v) = 0$ that there exists only one function $u = \varphi(v)$ such that $\varphi(0) = \varphi'(0) = 0$. Suppose the lowest power of the variable $v$ is $m$, and its coefficient is $l_{m}$, then $u = \varphi(v) = l_{m}v^{m}+l_{m+1}v^{m+1}+\cdot\cdot\cdot, \, m\geq2$. Therefore,

As a result, according to Theorem 7.1 in ^[33], $E_{1}(x_{1}, 0)$ is a saddle-node point.

If $r-a < \frac{bn}{\varepsilon c}$, the system will not have a positive equilibrium point. At this point, the system degenerates to $\frac{dx}{dt} = x(r-a-bx)$, and its positive equilibrium point is globally asymptotically stable. So, the boundary equilibrium point $E_{1}$ of the system is a globally asymptotically stable node, indicating the survival of the prey and the extinction of predators.

(iii) It is not difficult to confirm that the two eigenvalues $\lambda_{1}$ and $\lambda_{2}$ of $J(E^{*})$ satisfy

This indicates that both eigenvalues have negative real parts, so $E^{*}$ is a locally stable node. Now let's consider the Dulac function $B(x, y) = \frac{1}{xy}$. By simple calculation, we have

The Dulac-Bendixson theorem states that the system does not have a closed orbit, and since $E^{*}$ is the unique internal equilibrium point, every positive solution will tend toward $E^{*}$. This, along with the local stability state mentioned above, implies that it is a globally asymptotically stable node, ensuring the survival of both species. □

The proposition shows that as the parameter $r$ increases, the system's equilibria follow two paths. When $r\in(0, a)$, $E_{0}$ is the unique equilibrium point, which is a globally asymptotically stable node. When $r$ passes through $a$ to enter $(a, a+\frac{bn}{\varepsilon c})$, $E_{0}$ loses its stability to a globally asymptotically stable $E_{1}$; and when $r$ further passes through $a+\frac{bn}{\varepsilon c}$, $E_{1}$ loses its stability to a globally asymptotically stable $E^{*}$. When a new equilibrium point emerges, it will inevitably lead to the loss of stability of the previous equilibrium point, and the new equilibrium point will be globally asymptotically stable. The proposition also demonstrates that the fear effect has no impact on the stability of the system.

Theorem 2.1. The dynamics of the system depend on the intrinsic growth rate of the prey. There are two critical values of $0$ and $\frac{nb}{\varepsilon c}$. When it is less than the first critical value, both species will become extinct. When it is between the two critical values, the prey survives while the predator becomes extinct. When it is greater than the second critical value, both species survive.

2.1.2.   The impact of the fear effect on the system

Furthermore, we note that the expression $x^{*} = \frac{n}{\varepsilon c}$ is independent of the fear factor, indicating that the fear effect does not change the density of the prey. We will now focus on the effect of the fear effect on predators. First, we will examine the effect of $s_{1}$ on $y^{*}$. Let

then,

Because $q-\varepsilon c^{2}p = \varepsilon c^{2}(p-2k_{3}) > 0$, we have

Therefore,

We also investigated the impact of $s_{2}$ on $y^{*}$ and obtained similar results. For this reason, let

then,

Therefore,

The above discussion indicates that the density of predators will monotonically decrease as parameters continue to increase, eventually leading to extinction. We can observe that the presence of the fear effect only results in a shift in the location of the positive equilibrium point.

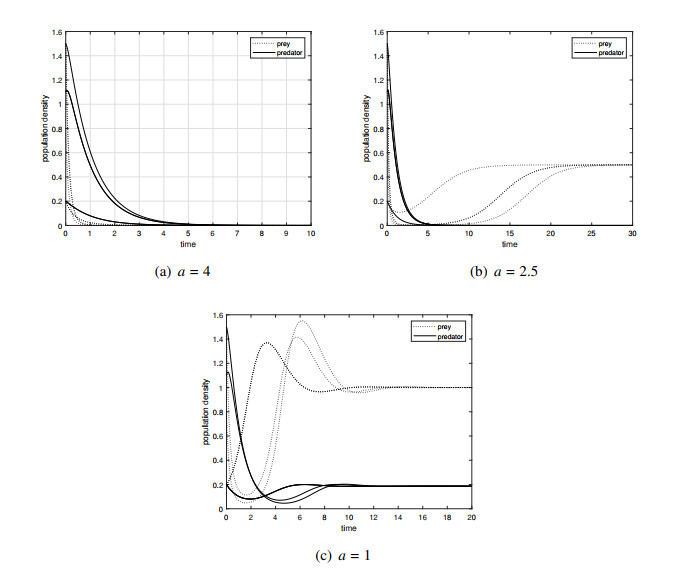
Example 2.1. Letting $r = 3, b = 1, n = 1, c = 2, \varepsilon = 0.5, s_{1} = 1, s_{2} = 1$. Fix the parameter $r$, and then let $a$ take different values so that they fall into the interval $(0, 2)$, $(2, 3)$, and $(3, +\infty)$, separately. Figure 1 shows that as $a$ decreases, the predator and prey populations go from initial total extinction to predator-only extinction, and then to coexistence. When the birth rate of the prey is lower than the mortality rate, it will inevitably lead to its ultimate extinction. At this point, specialist predators will inevitably become extinct due to a lack of food (Figure 1(a)). When the birth rate of the prey is greater than the mortality rate, the prey will continue to survive (Figure 1(b) and 1(c)). At this point, predators may exhibit two different states. If the energy gain obtained by predators from the prey cannot offset its natural death due to the low density of the prey, the predator will still eventually become extinct (Figure 1(b)). Otherwise, predators will continue to survive (Figure 1(c)). In each case, the newly emerging equilibrium point is always globally asymptotically stable.

Letting $r = 3, a = 1, b = 1, n = 1, c = 2, \varepsilon = 0.5$. Figure 2 illustrates the influence of parameters $s_{1}$ and $s_{2}$ on the system. It can be seen from the figure that as the corresponding parameters increase, the density of predators will decreases, while there is no effect on the density of the prey. Figure 2(a) shows the dynamics of the system when $s_{2} = 1$ is fixed. This indicates that different levels of fear effects will not alter the fact that two populations coexist, nor will they alter the density of the prey. When the level of fear is fixed ($s_{1} = 1$), the different levels of impact of fear on prey mortality also exhibit similar results (Figure 2(b)). Furthermore, we note that when one of these two parameters is fixed, the density of predators decreases to different levels as the other parameter increases. This indicates that fear can lead to an increase in the evasion behavior of the prey, thereby reducing its probability of being preyed upon, lowering the success rate of predators, and ultimately leading to a decrease in predator density. Also, both populations take longer time to reach the final states.

We summarize the theoretical analysis above into the following Theorem 2.2.

Theorem 2.2. (i) Fear factors do not change the dynamics of the system and the density of the prey; (ii) Fear factors can lower the density of predators.

The author in ^[31] believed that the outcome of fear will increase the density of the prey over a long period of time. However, our research results are very different: fear does not affect the density of the prey. This may be because, although the prey avoids predation by predators, due to other factors such as environmental or resource limitations, it does not change its environmental capacity. In addition, this study has shown that fear reduces the density of predators, which can be explained by the fact that when the prey perceives fear, they choose to stay away from the predator, making the predatory process more difficult, thereby achieving the effect of reducing predator density. The partial results of Theorem 2.2 are similar to those of ^{[21,24,26,27]}. From the perspective of biological conservation, there are certain situations in which such actions should be permitted. For instance, if predators consists of an invasive species, we can manipulate specific parameters to ultimately eradicate it. However, most of the time, we want two populations to coexist to maintain the diversity of the ecosystem. We are examining the net growth rate of predator populations by increasing their cooperative hunting efforts in the hope of controlling predator numbers to some extent.

2.2.   In the case of cooperative hunting in the system

In this case, the system always has two equilibrium points $E_{0}$ and $E_{1}$, which are identical to those in the system without cooperative hunting. By analyzing the equilibrium points $E_{0}$ and $E_{1}$ in the same manner, we can establish the stability of both equilibrium points.

2.2.1.   The existence and stability of positive equilibrium points

Next, we consider the existence of positive equilibrium points. The positive equilibrium points $\bar{E}(\bar{x}, \bar{y})$ are the solutions of the following system of equations:

From the second equation of (2.3), we know that $x = \frac{n}{\varepsilon (c+ey)}$. By substituting it into the first equation, we know that $\bar{y}$ are the positive roots of the equation

where

The equation can have at most two positive roots, depending on the signs of $\sigma_{3}$ and $\sigma_{4}$. For this, we define the function

Now, we will find the positive roots of Eq (2.4) by examining the positive zero points of the function $h(y)$. The derivative of $h(y)$ is

If $\sigma_{3}\geq 0$, then for any $y > 0$, there is $h'(y) > 0$. The function $h(y)$ is monotonically increasing on the interval $(0, +\infty)$, and $h(y) > h(0) = \sigma_{4}$. Note that as $\lim\limits_{y\rightarrow +\infty}h(y) = +\infty$, the function $h(y)$ has no positive zero root if $\sigma_{4}\geq0$, and has a single positive zero root if $\sigma_{4} < 0$.

The subsequent analysis indicates that the function $h'(y)$ must be monotonically increasing on the interval $(0, +\infty)$. The discriminant for the quadratic equation $h''(y) = 12\sigma_{0}y^{2}+6\sigma_{1}y+2\sigma_{2} = 0$ is $\Delta = 12(3\sigma_{1}^{2}-8\sigma_{0}\sigma_{2})$. If $\Delta > 0$, then the equation $h''(y) = 0$ has two distinct real roots, denoted as $y_{1}$ and $y_{2}$. Both of these real roots are negative. Without loss of generality, we assume that $y_{1} < y_{2} < 0$. Thus, the function $h'(y)$ monotonically increases in the interval $(y_{2}, +\infty)$. If $\Delta\leq0$, for any $y\in R$, there is $h''(y)\geq0$. The function $h'(y)$ monotonically increases over the interval $(-\infty, +\infty)$.

If $\sigma_{3} < 0$, it is obvious that $h'(0) = \sigma_{3} < 0$. Note that as $\lim\limits_{y\rightarrow +\infty}h'(y) = +\infty$, the equation $h'(y) = 0$ always has a unique positive root, denoted as $y_{3}$. In fact, $y_{3}$ is the real root that always exists in the cubic equation $h'(y) = 0$, and it has the following expression:

So, the function $h(y)$ monotonically decreases in the interval $(0, y_{3})$ and monotonically increases in the interval $(y_{3}, +\infty)$. If $h(0) = \sigma_{4}\leq0$, then the function $h(y)$ has a single positive zero root. If $h(0) > 0$, then the function $h(y)$ has no positive zero root if $h(y_{3}) > 0$, a single positive zero root if $h(y_{3}) = 0$, and two distinct positive zero roots if $h(y_{3}) < 0$.

Proposition 2.2. We have the following statement regarding the existence of positive equilibrium points:

(i) The system does not have a positive equilibrium point if $\sigma_{3}\geq0$, $\sigma_{4}\geq0$ or if $\sigma_{3} < 0$, $\sigma_{4} > 0$, and $h(y_{3}) > 0$ holds.

(ii) The system has a unique positive equilibrium point if $\sigma_{3}\geq0$, $\sigma_{4} < 0$ or if $\sigma_{3} < 0$, $\sigma_{4}\leq0$, or if $\sigma_{3} < 0$, $\sigma_{4} > 0$ and $h(y_{3}) = 0$ holds.

(iii) The system will have two positive equilibrium points if $\sigma_{3} < 0$, $\sigma_{4} > 0$, and $h(y_{3}) < 0$ holds.

The $E^{*}$ must be globally asymptotically stable as long as it exists. However, the stability of the $\bar{E}$ will become more complex. The Jacobian matrix of the system at $\bar{E}$ is given by

The local stability of $\bar{E}$ depends on the trace and determinant values of matrix $J(\bar{E})$, where

We substitute $\bar{x} = \frac{n}{\varepsilon (c+e\bar{y})}$ into $Det(J(\bar{E}))$ for convenience and use functions $f(y)$ and $g(y)$ to determine the signs of the trace and determinant. The expressions for $f(y)$ and $g(y)$ are determined by

Proposition 2.3. Suppose $\bar{y}$ is the solution of Eq (2.4). Then $\bar{E}(\bar{x}, \bar{y})$ is a saddle point if $f(\bar{y}) < 0$ holds, a stable node if $f(\bar{y}) > 0$ and $g(\bar{y}) < 0$ hold, and an unstable node if $f(\bar{y}) > 0$ and $g(\bar{y}) > 0$ hold.

2.2.2.   The impacts of the fear effect and cooperative hunting on the system

The expression $\bar{x} = \frac{n}{\varepsilon (c+e\bar{y})}$ gives the relationship between $\bar{x}$ and $\bar{y}$. A decrease in one population's position must be accompanied by an increase in the other's position. This is not what happens when predators fail to cooperate.

To investigate the impact of parameters on the equilibrium position, we analyze $\bar{y} = \bar{y}(s_{1}, s_{2}, e)$ and derive the following equation:

Taking the partial derivatives of $s_{1}$ on both sides, we get

Notice that $\sigma_{3}$ can be positive or negative. Therefore, the density of predators decreases while the density of the prey increases if $G_{2}(s_{1}) > 0$. The conclusion is reversed if $G_{2}(s_{1}) < 0$. Specifically, fear does not alter the density of two species if $G_{2}(s_{1}) = 0$. This indicates that fear may have no effect on population density, or have a positive or negative impact.

If we consider $s_{2}$ as an argument, we have

As a result, the density of predators will continue to decline. Combined with the previous discussion, we know that even though an increase in the parameter $s_{2}$ leads to a continuous increase in the density of predators, it will never exceed $\frac{r-a}{b}$.

To look at the impact of cooperative hunting on the system, we can take partial derivatives of $e$ on both sides,

The influence of cooperative hunting on the system depends on the sign of $H_{1}(e)$ and $H_{2}(e)$. The density of predators decreases as the density of the prey increases when $H_{1}(e)H_{2}(e) > 0$. The conclusion is reversed if $H_{1}(e)H_{2}(e) < 0$. Specifically, if $H_{1}(e) = 0$, then the cooperative hunting does not affect the density of the two populations. This demonstrates that when the strength of cooperative hunting falls within a certain range, increasing the density of predators will be advantageous.

Example 2.2. Let $r = 3, a = 1, b = 1, n = 1, c = 2, \varepsilon = 0.5, s_{1} = 1, s_{2} = 1$. When the strength of hunting cooperation is small ($e = 2$), the unique internal equilibrium point $\bar{E}(0.8304, 0.2042)$ is stable (Figure 3). As the strength of cooperative hunting increases, it makes the internal equilibrium point unstable and the periodic oscillation of different amplitudes appears (Figure 4(a)). When the strength of cooperative hunting is further strengthened, the periodic oscillation of the system shows a steady state, and a stable limit cycle appears (Figure 4(b)). This example indicates that cooperative hunting may be an unstable force (the internal equilibrium point unstable) or a stable force (a stable limit cycle) in the system. In addition, Figure 4(b) also shows that with the increase of parameter $e$, the density of predators no longer presents monotonicity, but increases first and then decreases. At this point, the blue curve in Figure 4(a) will change from right to left, indicating that the density of the prey is monotonically decreasing.

Example 2.3. Let $r = 3, a = 1, b = 1, n = 1, c = 2, \varepsilon = 0.5, s_{2} = 1$. We mainly investigate the effects of fear effects and cooperative hunting on the system when the internal equilibrium point is globally asymptotically stable. In Figure 5(a), $e = 0$ and $e = 2$ correspond to the red and black solution curves, and in Figure 5(b), $s_{1} = 0$ and $s_{1} = 2$ correspond to the red and black solution curves, respectively. From Figure 5(a), it can be seen that the number of prey decreases while the number of the predator slightly increases. This indicates that cooperative hunting, as a widely existing form of hunting among individuals within a species, has an extremely important significance in protecting rare or even endangered predators. As in ^[22], the authors obtained the result that the fear effect would simultaneously reduce the population density of both predator and prey. However, we draw an interesting and different conclusion based on the following analysis: the fear effect makes the system more stable. Figure 5(b) shows that the presence of the fear effect increases the final density of the prey and reduces the final density of predators, which makes it less likely to become extinct due to the increase in available resources possessed by each predator, despite a decrease in their final density. In addition, we believe that the increase in prey density is attributed to the fact that, although the fear effect can reduce the birth rate and increase the mortality rate of the prey, the amount of decrease in birth rate is smaller than the amount of increase in mortality rate, resulting in a higher net growth rate than the system without the fear effect. Overall, increase of fear effect and cooperative hunting makes the density of two species show the opposite trend.

Theorem 2.3. (i) Cooperative hunting can be a stable or unstable force in the system.

(ii) Both the fear and cooperative hunting may have no effect on population density, or have a positive or negative impact.

The authors of ^[19,23], as well as most other scholars, believe that fear reduces the densities of two species, which is significantly different from our result in Theorem 2.3. First, fear increases or decreases the density of the prey, depending on the value of its parameters, which contradicts the majority of research and common sense on fear. The reason is that, although fear simultaneously reduces the birth rate and mortality rate of the prey population, the degree of reduction varies, which leads to an increase in the net growth rate of the prey and an increase in its density. Second, the impact of fear on the density of predators and the prey will not be synchronous.

3.   Bifurcation analysis

Theorem 3.1. Regardless of whether there is cooperative hunting among predators, the system experiences a transcritical bifurcation at the trivial equilibrium $E_{0}$ as the parameter $r$ passes through the bifurcation value $r = r^{SN} = a$.

Proof. The proof that there is no cooperative hunting among predators is similar to having cooperative hunting. The Jacobian matrix with $r = r^{SN}$ at $E_{0}$ is

Obviously, the matrix $A$ has a single eigenvalue $\lambda = 0$ with eigenvector $V$, and $A^{T}$ has an eigenvector $W$ corresponding to the eigenvalue $\lambda$. After a simple calculation, we get $V = W = (1, 0)^{T}$, and

Therefore,

According to Sotomayor's theorem in ^[35], the system experiences a transcritical bifurcation at $E_{0}$ as the parameter $r$ crosses the bifurcation value $r^{SN}$. □

Theorem 3.2. Let $e_{SN}$ be the solution of the equation $g(\bar{y}(e)) = 0$. The system experiences a Hopf bifurcation around $\bar{E}$ at $e = e_{SN}$ if $Det(\bar{x}(e), \bar{y}(e)) > 0$ and $\frac{d}{de}(Tr(\bar{x}(e), \bar{y}(e)))\neq 0$ at $e = e_{SN}$.

Proof. The secular equation of the Jacobian matrix about the equilibrium $\bar{E}$ is $\lambda^{2}-Tr(J(\bar{E}))\lambda+Det(J(\bar{E})) = 0$. For Hopf bifurcation, the matrix $J(\bar{E})$ must have a pair of purely imaginary eigenvalues. So, the characteristic equation becomes $\lambda^{2}+Det(\bar{x}(e), \bar{y}(e))\mid_{e = e_{SN}} = 0$. If $Det(\bar{x}(e), \bar{y}(e))\mid_{e = e_{SN}} > 0$, the above characteristic equation has a pair of purely imaginary eigenvalues $\lambda_{1, 2} = \pm i\theta_{0}$, where $\theta_{0} = \sqrt{Det(\bar{x}(e), \bar{y}(e))\mid_{e = e_{SN}}}$. To verify the transversality condition, we consider the any neighbouring point $e$ of $e_{SN}$, the eigenvalues are $\lambda_{1, 2} = \rho(e)\pm i\theta(e)$, where

Now, $\eta = \frac{d}{de}(\rho(e))\mid_{e = e_{SN}} = \frac{1}{2}\cdot\frac{d}{de}(Tr(\bar{x}(e), \bar{y}(e)))\mid_{e = e_{SN}}$. Hence, the system experiences a Hopf bifurcation around $\bar{E}$ at $e = e_{SN}$ if $\frac{d}{de}(Tr(\bar{x}(e), \bar{y}(e)))\mid_{e = e_{SN}}\neq 0$. □

The $1^{st}$ Lyapunov coefficient needs to be calculated to determine the direction of Hopf bifurcation. First, we transform $\bar{E}$ into the original by letting $w_{1} = x-\bar{x}$ and $w_{2} = y-\bar{y}$.

Expanding Taylor's series of the above system at $(w_{1}, w_{2}) = (0, 0)$ up to terms of order 3 produces the following system:

where

If 4th order and above terms are omitted, the system (3.1) can be rewritten as

where

For Hopf bifurcation, the characteristic equation becomes

$\lambda_{1, 2} = \pm i\theta_{0}$ are the two roots of the equation, where $\theta_{0} = \sqrt{Det(J(\bar{E}))|_{e = e_{SN}}}$ if $Det(J(\bar{E})) > 0$ at $e = e_{SN}$. The eigenvector of matrix $J(\bar{E})$ belonging to eigenvalue $i\theta_{0}$ at $e = e_{SN}$ is $\bar{v} = (p_{01}, i\theta_{0}-p_{10})$. Define

Let $Z = A^{-1}U$, where $Z = (z_{1}, z_{2})^{T}$. Then, the system (3.2) becomes

This can be written as

The remaining parts of $P^{1}$ and $P^{2}$, apart from the linear parts of $z_{1}$ and $z_{2}$, are given by the following expression:

with

Substituting $p_{30} = p_{21} = q_{20} = q_{21} = q_{30} = q_{03} = 0$ into $F_{1}$ and $F_{2}$, we get

The $1^{st}$ Lyapunov coefficient based on the normal form (3.3) is

By applying the result given in ^[36], Hopf bifurcation is supercritical if $R < 0$ and it is subcritical if $R > 0$.

4.   The existence of bistability

Cooperative hunting may increase the number of equilibrium points in the system. Just as the Proposition 2.2 indicates, system (1.1) can have at most two positive equilibrium points. When there are two distinct positive equilibrium points, the system may exhibit bistability. The bistable state here refers to a stable limit cycle and a stable node. We found through numerical simulation that one of the positive equilibrium points is an unstable node, and there is a stable limit cycle around it. In addition, the semi-trivial equilibrium point is a locally stable node.

Example 4.1. If $r = 10, a = 0.1, b = 0.9, n = 1, c = 0.01, \varepsilon = 0.4, s_{1} = 0.1$, and $s_{2} = 0.2$, then the system has four equilibrium points (intersection point of solid line and dotted line in Figure 6(a)), one of which is the origin, one is the boundary equilibrium point, and two are positive equilibrium points. When the initial density of the prey is fixed ($x_{0} = 15$), let the initial density of predators change from 0.1 to 3.7 in steps of 0.05, and $(x_{0}, y_{0}) = (1, 2.6)$ and $(6.6, 1.6)$, the phase diagram of the system is obtained (Figure 6(b)). The green trajectory gradually moves away from the positive equilibrium point, indicating that the equilibrium point it surrounds is an unstable node. In addition, when the time is large enough, the green, yellow, and magenta trajectories all exhibit periodic oscillations (Figure 6(c)), indicating the existence of at least one stable limit cycle and one unstable limit cycle within the area surrounded by the magenta trajectories. We can also know from Figure 6(b) and 6(d) that the other positive equilibrium point is saddle point and the boundary equilibrium point is a locally stable node point. In brief, under this set of parameter values, predators exhibit two states: extinction or survival. The reason for the extinction of predators may be that they are unable to offset their mortality rate through predation (red trajectories) or, although predators can offset their mortality rate through predation in the short term, an increase in their numbers can lead to a sharp decline in the number of prey, making it unable to meet their own growth needs (black trajectories). In this situation, in order for two populations to coexist, the density of the prey must exceed a certain critical value (such as the first component of the right positive equilibrium point), and the initial density of the predator cannot be too small or too large (between 0.25 and 2.25). In order to understand the impact of the strength of cooperative hunting on system dynamics when there are two positive equilibrium points, while keeping other parameters remain unchanged, the strength of cooperative hunting of 5 is taken to obtain Figure 7. Just like when $e = 1$, there are also four equilibrium points. By comparing Figures 6 and 7, we found the following differences. First, both positive equilibrium points of are unstable nodes, and the boundary equilibrium point is saddle point (Figure 7(b)). Second, all trajectories ultimately exhibit periodic solutions with the same amplitude (Figure 7(c) and 7(d)). This indicates that only one stable limit cycle exists.

As the strength of cooperative hunting increases, trajectories will shift from periodic oscillations of different amplitudes to periodic oscillations of the same amplitude, and from the existence of stable and unstable limit cycles to the existence of a unique stable limit cycle. In this sense, we can say that cooperative hunting can enhance the stability of the system. Also, a higher strength of cooperative hunting can ultimately lead to the coexistence of two species. This is because as the strength of cooperative hunting increases, the boundary equilibrium point loses its stability (saddle point), and stable periodic oscillations occur in the vicinity of it.

5.   Discussion

The system we study in this paper proposes that the perceived risk of predation in prey populations not only reduces their birth rate, but may also lead to an increase in mortality.

If only the fear is considered, the system has a relatively simple dynamic, that is, the newly emerged equilibrium point must be globally asymptotically stable. The conclusion was drawn that fear only reduces predator density, and does not affect system dynamics and prey density, which is similar to the research results of other scholars, such as ^[21,24,27], on the fear effect models. In this case, both species will only exist in three states, namely extinction of both, or survival of the prey and extinction of predators, or coexistence.

When predators engage in cooperative hunting, the system exhibits completely different dynamic behaviors. According to Proposition 2.2 and Example 4.1, the number of equilibrium points may increase, some of which are stable and some are not. If the positive equilibrium point is unstable, there may be a bifurcation near it, which may lead to stable or unstable limit cycles. The research results also indicate that both the fear and cooperative hunting can be a stable or unstable force in the system. When there is a fixed level of fear, increasing the strength of cooperative hunting will make the system unstable around the positive equilibrium point and experience subcritical Hopf bifurcation, resulting in limit cycles oscillations dependent on the initial values. These limit cycle oscillations are ultimately replaced by a stable limit cycle. This indicates that cooperative hunting may be an unstable force (disrupting the stability of the positive equilibrium point) or a stable force (from limit cycle oscillations to a stable limit cycle). In addition, cooperative hunting has a positive impact on predators and a negative impact on the prey, as it increases the density of predators and decreases the density of the prey. Compared to the impact of cooperative hunting on the system, the impact of the fear on the system may be exactly the opposite. For example, the fear of predators by the prey can increase its density, which is different from the results of all previous scholars, and is a new discovery in our study of the fear effect. Another new finding is that fear has an opposite effect on the densities of two species, which is different from the result in ^[19] in which fear synchronously reduces the densities of both species. We provide a biological explanation for the reason why fear leads to an increase in the prey density in Example 2.3.

Finally, through numerical simulations, it was found that fear prolongs the time for a species to reach a survival state and accelerates the process of extinction. Cooperative hunting can also have an impact on the progress of species.

6.   Conclusions

All animals, regardless of their phyla, should pay attention to predators. Even tigers have to watch out for humans. Fear is a very powerful evolutionary force. The challenge of studying the fear effect is that even if behaviors related to fear effects can be observed, we cannot observe how fear reduces the birth and mortality rates of the prey. We can only infer its impact from a theoretical perspective. In this article, we addressed a predator-prey model of cooperative hunting in which fear simultaneously reduces the birth and mortality rates of the prey, to reveal the effects of fear and cooperative hunting on population evolution. Through discussion and analysis of a specific model, some new conclusions have been obtained. We can emphasize that both fear and cooperative hunting have the potential to have a positive effect. From the ecological point of view of our study, predators can adjust the intensity of fear through cooperative hunting or through sound, smell, etc., so as to achieve the purpose of adjusting the prey density. This dynamic adjustment may have significant implications for regional ecosystems and may even cause a "trophic cascade" effect. The focus of our work is to discuss theoretically how fear works, not whether it is real or not. Such research will provide a basis for protecting population size or reintroducing new populations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Natural Science Foundation of China (No. 11801291), the Natural Science Foundation of Fujian Province (No. 2021J011155) and the Education and Research Project for Middle and Young Teachers of Fujian Province (No. JAT210461).

Conflict of interest

The authors declare that they have no conflicts of interest.