1.
Introduction
The transmission eigenvalue problem appears in inverse scattering theory and has attracted wide attention recently (see, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] and the references therein). It is non-self-adjoint and irregular in the Birkhoff (and even the Stone) sense [17]. According to the incident fields and the measuring positions, the transmission eigenvalue problem can be divided into the interior transmission eigenvalue problem and the exterior transmission eigenvalue problem. The subject matter of this paper is the latter problem which plays a central role in many important physical problems, such as the inverse scattering problems of determining the shape of underground reservoirs or nuclear reactors [18].
The exterior transmission eigenvalue problem for spherically stratified media in R3 (see [19,20]) is to find functions w,v∈C2(R3∖¯D) such that
where r:=|x|, x∈R3, D:={x:|x|<a}, ν is the unit outward normal to ∂D, n∈W22(a,b), n(r)>0 for a<r<b and n(r)=1 for r>b. Values of k∈C such that there exists a nontrivial solution to (1.1)–(1.6) are called exterior transmission eigenvalues.
In this paper, not all the exterior transmission eigenvalues but a subset consisting of those eigenvalues for which the corresponding eigenfunctions are spherically symmetric are considered. Let
then the relations (1.1)–(1.6) become the following ordinary differential equations
and
It is known that the transmission eigenvalues carry information about the refractive index and are used in sampling type methods for the reconstruction of the support of an inhomogeneous medium (for details, see [21,22]). The interesting and important questions are the distribution of the transmission eigenvalues. For the interior transmission eigenvalue problems, Xu and his collaborators gave the asymptotics of non-real transmission eigenvalues in [23,24]. For the exterior transmission eigenvalue problems, Chen [25] described a asymptotic eigenvalue density for each scattered angle. In [15], we showed that there are infinitely many non-real eigenvalues and gave the asymptotics of exterior transmission eigenvalues without the description of the subscript numbers. Recently, several intrinsic local and global geometric patterns of the transmission eigenfunctions have been revealed. The local geometric property was first discovered and investigated in [26,27], and was further studied in [28,29,30,31] for different geometric and physical setups. The global geometric property was first discovered and investigated in [32], and was further studied in [33,34,35] for different geometric and physical setups.
In this paper, we continue to study the asymptotic behavior which is more accurate than that in [15]. Furthermore, the asymptotic behavior in this paper is described by the subscript numbers. The asymptotics of eigenvalues with the description of the subscript numbers is more difficult to investigate (due to the non-self-adjointness), but it has important applications in the inverse spectral problems, especially in the inverse spectral problem with the mixed spectral data and the stability of the inverse spectral problem [5,14,17,36,37,38].
The paper is organized as follows. In Section 2, we study the asymptotics of the characteristic function and give the asymptotic solution of a transcendental equation. Then, we concern the counting results and the asymptotic behavior of exterior transmission eigenvalues for the case when n(a)≠1, n(b)≠1 in Section 3 and for the case when n(a)=1,n(b)≠1 and the case when n(a)≠1,n(b)=1 in Section 4.
2.
Preliminaries
Firstly, we reduce the eigenvalue problem (1.7)–(1.11) to a problem of finding roots of a relative function, which is referred to as the characteristic function in the following. It appears in [15] and we give it without proof.
Lemma 2.1. The exterior transmission eigenvalues coincide with the zeros of the function D(k), where
and Y(r,k) is the unique solution of the initial value problem
In order to look for the properties of the characteristic function D(k), we now give the behaviours of Y(r,k) and Y′(r,k). Make use of the modified Liouville transformation
and define the quantity
which has a physical meaning as the travel time for a wave to move from r=a to r=b in the corresponding wave scattering problem. The problem (2.2) is transformed in the following form [15]
where
Let z1(ξ) and z2(ξ) be the solutions of (2.6) which satisfy z1(0)=1,z′1(0)=0 and z2(0)=0, z′2(0)=1. Then z(ξ) can be represented in the form
By using (2.4) and (2.1), we calculate that
and then
where
From the basic estimates in Chapter 1 of [39], we know that if p∈L2[0,γ],
if p∈W12[0,γ],
and if p∈W22[0,γ],
where
A straightforward computation yields the following asymptotic expansions for D(k),
and
where
Note that (2.20) can be rewritten as
To get the asymptotics of the non-real exterior transmission eigenvalues, we introduce the following transcendental equation:
where κ is a constant in C and lnz=ln|z|+iargz with −π<argz≤π.
Lemma 2.2. The transcendental Eq (2.27) has a unique solution
for any sufficiently large |w|.
Proof. The proof can be found in [24].
3.
The distribution of the exterior transmission eigenvalues
Based on our previous results about the asymptotics of the exterior transmission eigenvalues [15], we continue to focus on more precise asymptotics with the description of the subscript numbers. When we count the exterior transmission eigenvalues, we always count the multiple zeros (if there exist) with their multiplicities. Below, the standard notation
is used for the norm on L2[0,γ].
3.1. The case when n(a)≠1 and n(b)≠1
Define
The conditions n(a)≠1 and n(b)≠1 imply that
and
It follows that the function g1(k) has zeros in C. Since c1−c2c1+c2>0 if [n(a)−1][n(b)−1]>0 and c1−c2c1+c2<0 if [n(a)−1][n(b)−1]<0, then the zeros of g1(k) are
where
and
Note that as k→∞,
and
Lemma 3.1. Suppose n∈W22(a,b) and n(a)≠1, n(b)≠1. Then
where A,B,C,D are defined as in (2.13), and
Proof. With the use of the Picard iteration method [39], we know that for ξ∈[0,γ],
where
and
Using (3.7) and (3.8) in (2.1) we obtain that
Recall the elementary inequalities
and
Then the terms on the right-hand side of (3.11) can be majorized as follows,
The value of the integral in the last line does not change under permutation of t1,…,tn, and the union of all the permuted regions of integration is [0,γ]n. It follows that
by the Schwarz inequality. Thus,
The same reasoning applies to the other terms and yields, for k∈C, p∈L2[0,γ],
Therefore,
This completes the proof.
The following lemma can be obtained for arbitrary sine-type functions (see Lemma 1 on page 163 in [40]). In order to facilitate the readers, we show the proof.
Lemma 3.2. Suppose n∈W22(a,b) and n(a)≠1, n(b)≠1. Let k0j, j∈Z, be the zeros of g1(k) defined in (3.2). For any ε>0, if |k−k0j|≥ε for all integers j, then there exists a number Mε>0, such that
Proof. We only prove the inequality (3.14) in the case when [n(a)−1][n(b)−1]>0, i.e., c1−c2c1+c2>0, the proof in the case when [n(a)−1][n(b)−1]<0 can be completed similarly.
Denote G1(k):=|g1(k)|2exp(−2|Imk|γ). Let k=x+iy. By a direct calculation, we have
Then if y≥0,
and if y≤0,
By use of the periodicity of the cosine function, we just need to prove that G1(k) has a positive lower bound when k∈Dε, where
Choose δ0∈(0,ε) such that
Firstly, let us consider the case when 0<|c1−c2c1+c2|<1, i.e., y0<0.
(a) For y≥0, we get e−2yγ≤1 and then
(b) For y∈(−∞,y0−δ0], we have e2γy≤e2γy0e−2γδ0=|c1−c2c1+c2|e−2γδ0 and
(c) For y∈(y0−δ0,y0], i.e., |c1−c2c1+c2|e−2γδ0<e2γy≤|c1−c2c1+c2|, the assumption |k−iy0|≥ε implies that
Hence
(d) We now consider the remaining case y∈(y0,0). If δ0<−y0, then (y0,0)=(y0,y0+δ0)∪[y0+δ0,0). For y∈(y0,y0+δ0)⊂(y0,0), we get |c1−c2c1+c2|<e2γy<1. Then
For y∈[y0+δ0,0), we obtain that |c1−c2c1+c2|e2γδ0≤e2γy<1, and then
If δ0≥−y0,then y∈(y0,0)⊂(y0,y0+δ0), |c1−c2c1+c2|<e2γy<1, and
Then, using the similar steps above, we can estimate the lower bound of G1(k) in the case when |c1−c2c1+c2|>1. More specifically,
and for the interval (0,y0),
or
Lastly, for |c1−c2c1+c2|=1, we similarly conclude that
To sum up, there exists a number Mε>0 such that G1(k)>M2ε for k∈Dε, i.e.,
This completes the proof.
Remark 3.1. If ε=π4γ, we can take δ0=π8γ to make the condition (3.19) true.
In this case, |1−e2γδ0|>|1−e−2γδ0|>12, √1+e−4γδ0−2cos2γ√ε2−δ20>12, and √1−cos2γ√ε2−δ20>12. Then Mε can be taken as follows:
For j∈N+, consider the rectangle contour Γ(1)j=I(1)1,j∪I(1)2,j∪I(1)3,j∪I(1)4,j, where
Fix j>12π|ln|c1−c2c1+c2||, then for all k∈Γ(1)j, we have that |k−k0j|≥π4γ, j∈Z. By Lemma 3.2 and Remark 3.1, we get that, if k∈Γ(1)j, j>12π|ln|c1−c2c1+c2||, then
Theorem 3.1. Suppose n∈W22(a,b), n(a)≠1, n(b)≠1. The values γ, K, M, c1,c2 appear in (2.5), (3.6), (2.21), (2.22) and (3.26) respectively. Let
be an integer. Then, if [n(a)−1][n(b)−1]>0, there are exactly 2N+2 exterior transmission eigenvalues, counted with multiplicities, inside Γ(1)N, if [n(a)−1][n(b)−1]<0, there are exactly 2N+1 exterior transmission eigenvalues, counted with multiplicities, inside Γ(1)N, and for each j>N, exactly one simple root in the circular region
where k0j are defined as in (3.2). There are no other roots.
Proof. Fix N be an integer that satisfies (3.28), and let L≥N be an integer. Consider the contours Γ(1)L and the contours
By Lemma 3.2 and Remark 3.1, the estimate |g1(k)|>Mexp(|Imkγ|) holds on all of them. Therefore, by the estimate for D(k) in Lemma 3.1,
also holds on them since |kγ|≥Nπ+π4 on them. Hence, by Rouché's theorem, D(k) has as many roots, counted with multiplicities, as kg1(k) in each of the bounded regions. Since g1(k) has only the simple roots
and L≥N can be chosen arbitrarily large, the theorem follows.
Since [g1(k)]∗=−g1(−k∗), where k∗ denotes the conjugate of k, then the distribution of the zeros of g1(k) is symmetrical with respect to the imaginary axes. Denote the zeros of D(k) by {kj}j≥0∪{−k∗j}j≥0 if [n(a)−1][n(b)−1]>0; by {kj}n≥0∪{−k∗j}n≥1 if [n(a)−1][n(b)−1]<0. Moreover, it follows from Lemma 3.2 that
Let us estimate ϵj, j≥0. Substituting (3.29) into (2.18), by a direct calculation, we have
where αj=O(1j). Since e−2ikjγ=c1−c2c1+c2e−2iϵjγ, we have that isin2ϵjγ+αj=0, and hence ϵj=O(1j).
If p∈W12[0,γ], then we can obtain the more accurate expression of ϵj. Indeed, substituting (3.29) into (2.19), we obtain
and then
where βj=O(1j).
By use of the expansions
we get that
Then, under the conditions n(a)≠1,n(b)≠1, the exterior transmission eigenvalues can be numbered and estimated as follows.
Theorem 3.2. Assume n∈W22(a,b), n(a)≠1,n(b)≠1. Denote the exterior transmission eigenvalues by {kj}j≥0∪{−k∗j}j≥0 if [n(a)−1][n(b)−1]>0; by {kj}j≥0∪{−k∗j}j≥1 if [n(a)−1][n(b)−1]<0. Then the sequence {kj}j≥0 has the following asymptotics:
where k0j, j∈Z, is the sequence defined as in (3.2). If we further assume p∈W12[0,γ], then the sequence {kj}j≥0 has the following asymptotics:
where the numbers c1,c2,d1,d2 appear in (2.21)–(2.24).
3.2. The case when n(a)=1,n(b)≠1 or n(a)≠1,n(b)=1
In this subsection, we first study the distribution of zeros of the function g2(k) defined in (3.30) below. And then, we get a counting lemma and the asymptotics of the exterior transmission eigenvalues. Note that c1+c2=0,c1−c2≠0 if n(a)=1,n(b)≠1, and c1+c2≠0,c1−c2=0 if n(a)≠1,n(b)=1. In both cases, the function g1(k) has no zeros at all.
If n(a)=1,n(b)≠1, then
Define
Then as k→∞, if p∈W12[0,γ],
and if p∈W12[0,γ],
Since the function g2(k) has only one zero k=−d1+d2c1−c2i if d1=d2, we further assume that d1−d2≠0, i.e., n′(a)≠0.
Lemma 3.3. If n(a)=1,n(b)≠1 and n′(a)≠0, then all zeros of g2(k), excepting one imaginary one, are simple algebraically.
Proof. Assume k0 be some zero of g2 with multiplicities at least two. Then we have from g2(k0)=0 and g′2(k0)=0 that
which implies that the function g2(k) has only one multiple zero. The proof is complete.
Now, let z=−2ikγ in (3.30). Then the equation 2ic1−c2keikγg2(k)=0 is equivalent to
which implies
By Lemma 2.2, we have
It follows that Rez=lnj+O(1), which implies
Since g2(−k∗)=−[g2(k)]∗, then the distribution of the zeros of g2(k) is symmetrical with respect to the imaginary axes. Let us consider the zeros of g2(k) with Rek>0, namely, assume j>0. Going back to (3.33), we have
and
Therefore, substituting (3.34)–(3.36) into (3.33), we have
Hence
and then
Hence we can obtain the expression of z which is more accurate than (3.37),
Denote the zeros of g2(k) by {μj}. Let μj=σj+iτj. Since z=−2ikγ, we have that if d1−d2c1−c2>0,
and if d1−d2c1−c2<0,
Let k=x+iy. Then
For sufficiently large j∈N+, consider the rectangle contour Γ(2)j=I(2)1,j∪I(2)2,j∪I(2)3,j∪I(2)4,j, where
Letting k start from the point ((j+1)πγ,−(j+1)πγi) and travel round Γ(2)j by the counterclockwise, and using (3.40), one can easily obtain that, for large enough j, if d1−d2c1−c2>0, i.e., n′(a)n(b)−1>0, then the variations
where θ1,θ2,θ3,θ4∈(0,π), and θ4=θ2+θ2+θ3; if d1−d2c1−c2<0, i.e., n′(a)n(b)−1<0, then the variations
where θ5,θ6,θ7,θ8∈(0,π), and θ5+θ6+θ7+θ8=2π. Thus, ΔΓ(2)narg2e−ikγkg2(k)c1−c2=4(j+1)π if n′(a)n(b)−1>0; ΔΓ(2)narg2e−ikγkg2(k)c1−c2=(4j+6)π if n′(a)n(b)−1<0. By the argument principal of entire functions, the number of zeros of the function kg2(k) inside Γ(2)j equals 2j+2 if n′(a)n(b)−1>0; equals 2j+3 if n′(a)n(b)−1<0. Therefore, the zeros of kg2(k) can be numbered as follows.
Lemma 3.4. If n′(a)n(b)−1>0, then the zeros of kg2(k), denoted by {μj}j≥0∪{−μ∗j}j≥0 with Reμj≥0, satisfy the asymptotic formula (3.38). If n′(a)n(b)−1<0, then the zeros of kg2(k), denoted by {μj}j≥0∪{−μ∗j}j≥1 with Reμj≥0, satisfy the asymptotic formula (3.39).
Next, we study the asymptotics of exterior transmission eigenvalues under the assumption p∈W12[0,γ] or p∈W22[0,γ]. In the latter case, we obtain the more accurate estimate for the asymptotics of exterior transmission eigenvalues. For arbitrary small ε>0 and large j, consider the rectangle contour Δj:=Δ±σj∪Δ±τj, where
Lemma 3.5. If n(a)=1,n(b)≠1 and n′(a)≠0, then for sufficiently large j>0, and small ε>0, the function g2(k) satisfies
where Cε>0 does not depend on j.
Proof. Denote G2(k):=|kg2(k)|2e−2|Imk|γ. Recall k=x+iy. By a direct calculation, we have
It follows that if Imk≥0,
and if Imk<0,
Let us first consider the case k∈Δj. From (3.38) and (3.39), we have Imμj>0, σje−2τjγ→|d1−d2c1−c2| as j→∞. It follows that when k∈Δ±τj,
and
here t∈[−ε,ε]. Substituting (3.42) and (3.43) to (3.41), we have that
Denote q1(t):=1+e∓4γε−2e∓2γεcos2tγ. It is easy to see that q1(t) has minimum value at t=0. Thus, we have
Similar to (3.44), we can obtain that for k∈Δ±σj,
where t∈[−ε,ε]. Denote q2(t):=1+e−4γt−2e−2γtcos2γε. Easily, q′2(t)>0 for cos2γε>e−2γt and q′2(t)<0 for e−2γt>cos2γε. Thus, it follows that
Together with (3.45) and (3.47), we have proved that there exists η1>0 that is dependent only on ε, such that G2(k)>η1 for k∈Δj.
Now, let up pay attention to the case k∈Γ(2)j. Because g2(k) satisfies g2(−k∗)=−[g2(k)]∗, we only need to consider k∈Γ(2)j∩{k:Rek≥0}.
For k∈{k:0≤x≤j+1γπ,y=j+1γπ}, we have
For k∈{k:x=j+1γπ,12γlnj<y≤j+1γ}, i.e., x=σj+j+1γπ−σj and y=τj+t with t∈[12γlnj−τj,j+1γ−τj], similar to (3.46), and using (3.38) and (3.39), we have
For k∈{k:x=j+1γπ,0≤y≤12γlnj}, we get
For k∈{k:x=j+1γπ,−j+1γ≤y<0}∪{k:0≤x≤j+1γπ,y=−j+1γπ}, we have
Together with (3.48)–(3.51), we obtain that there exists η2>0 that is independent on j, such that G2(k)>η2 for k∈Γ(2)j. Taking Cε=min{η1,η2}, we complete the proof.
Using Lemma 3.5 and (3.31), we get that |kg2(k)|>|D(k)−kg2(k)| for k∈Γ(2)j∪Δj for large j. By the Rouche's theorem, we conclude that the number of zeros of the function D(k) coincides with the number of kg2(k) inside Γ(2)j or Δj. It follows from Lemma 3.3 that all sufficiently large zeros of D(k) are simple. By Lemma 3.4, the zeros of the function D(k) can be numbered as follows: when n′(a)n(b)−1>0 denote the zeros of D(k) by {kj}j≥0∪{−k∗j}j≥0; when n′(a)n(b)−1<0 denote the zeros of D(k) by {kj}j≥0∪{−k∗j}j≥1. Moreover,
Furthermore, we estimate ϵj. Substituting (3.52) into (3.31), we get
where {αj}∈l2. Noting g2(μj)=0, i.e., iμje2iμjγ−d1+d2c1−c2e2iμjγ+d1−d2c1−c2=0. Then
Using the asymptotics of μj, we get e2iμjγ=O(1j). Then
and then ϵj=O(1j).
If p∈W22[0,γ], then we can substitute (3.52) into (3.32) and obtain that
where βj=O(1j). The fact g2(μj)=0 implies that
i.e.,
Since
then
hence,
Let us summarize what we have proved.
Theorem 3.3. Assume n(a)=1, n(b)≠1, n′(a)≠0, and p∈W12[0,γ]. Denote the exterior transmission eigenvalues by {kj}j≥0∪{−k∗j}j≥0 if n′(a)n(b)−1>0; by {kj}j≥0∪{−k∗j}j≥1 if n′(a)n(b)−1<0. Then the sequence {kj}j≥0 has the following asymptotics:
If we further assume p∈W22[0,γ], then the sequence {kj}j≥0 has the following asymptotics:
Here, the asymptotics of {μj} is given in (3.38) and (3.39), the numbers d1,d2,e1,e2 and the function p appear in (2.23)–(2.26) and (2.8).
When n(a)≠1, n(b)=1, n′(b)≠0, the asymptotics of exterior transmission eigenvalues can be studied similarly. Let
where
and
We provide the following theorem without proving it.
Theorem 3.4. Assume n(a)≠1, n(b)=1, n′(b)≠0 and p∈W12[0,γ]. Denote the exterior transmission eigenvalues by {kj}j≥0∪{−k∗j}j≥2 if n′(b)n(a)−1>0; by {kj}j≥0∪{−k∗j}j≥1 if n′(b)n(a)−1<0. Then the sequence {kj}j≥0 has the following asymptotics:
If we further assume p∈W22[0,γ], then the sequence {kj}j≥0 has the following asymptotics:
where {μ′j} is given in (3.54), the numbers d1,d2,e1,e2 and the function p appear in (2.23)–(2.26) and (2.8).
Remark 3.2. When n(a)=1 and n(b)=1, the asymptotics of the exterior transmission eigenvalues can be studied similarly according to whether n′(a) and n′(b) are zeros.
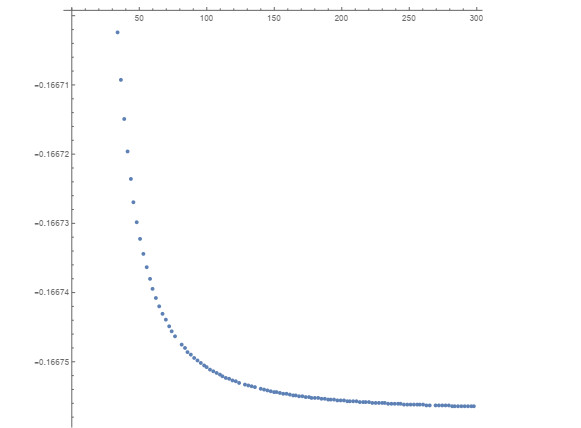
Example 3.1. If n(r)=1r4,a=12,b=32, then n(a)=24≠1, n(b)=(23)4≠1, γ=∫ba√n(t)dt=43, p(ξ)=14n′′(r)n(r)2−516n′(r)2n(r)3=0, and
By use of Theorem 3.2, we have
and they are near the line z=3i8ln2539≈−0.166757i for k large enough. Figure 1 shows the numerical distribution of the zeros of D(k), which are the eigenvalues in (3.55).
Acknowledgments
This work was supported by the National Natural Science Foundation of China (12201460 and 12001153).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:



