Image restoration by using a modified proximal point algorithm

1.   Introduction

Convex optimization, a branch of mathematical optimization, examines the problem of minimizing convex functions over convex sets, which has several applications in a variety of fields, including image processing, automatic control systems, data analysis, and finance. The idea of convex minimization is to determine $x^{*}$ in closed convex subset $K$ in a real Hilbert space $H$. Then

where a convex function $h:K\to \mathbb{R}$. $\arg\min_{y\in K}h(y)$ represents the minimization set of $h$ on $H$. Note that if $h$ is a differentiable function on $K$, then $x^{*}$ is a solution of (1.1) is also a solution of the variational inequality problems (see in ^[1]), that is, to find $x^{*}\in K$ such that $\langle h'(x^{*}), x-x^{*}\rangle \geq 0, \, \forall x \in K.$ In 1970 and 1976, Martinet ^[2] and Rockafellar ^[3] presented a tool for finding the solution of (1.1). That is the proximal point algorithm (PPA), which is given by

where $0 < \lambda_{n}$ for every $1 \leq n$. They also demonstrated that this algorithm yields a sequence $x_n$ that weakly converges to a $h$ minimizer. Later, a growing number of researchers have been investigating solutions to the convex minimization problem (see in ^{[4,5,6,7,8,9]}).

Another interesting problem is the variational inclusion problem (VIP). That is to find $x\in H$,

where operator $F$ is single-valued on $H$ and $G$ is multi-valued mappings on $2^{H}$. We denote that $(F+G)^{-1}(0)$ is the set of solutions of (1.2). When setting $F\equiv0$, (1.2) becomes the monotone inclusion problem (in ^[3]) which is a generalization of the variational inequality problem (formore information, see ^[10]). It is well-known that the problem (1.2) provides a general and convenient framework for the unified study of optimal solutions in many optimization related areas such as mathematical programming, variational inequalities, optimal control and many others. There are a lot of methods to solve VIP (see in^{[11,12,13,14]}). The forward-backward splitting method is one of the most well-known (see in ^[12,13]), as demonstrated by the following:

where $\lambda_{n} > 0, \, D(G)\subset D(F)$, $F$ is inverse strongly monotone and $G$ is monotone Lipschitz continuous. Furthermore, the methodology (1.3) refers to $\{x_{n}\}$ that converges to a VIP solution only weakly. After that, researchers focus on adapting monotone operators to handle zero points of monotone operators (for more detail see in ^{[4,6,12,15,16,17]}). In 2016, Boikanyo ^[18] introduced the viscosity approximation forward-backward splitting technique, a development on the proximal point methodology for estimating a zero point for a coercive operator $F$ and maximum monotone operator $G$.

Recently, Sow ^[19] focused on establishing an algorithm based on the methods of ^[3] and ^[18] for determining a point in the common solution of a convex optimization problem and VIP, that is, $\arg\min_{u\in K}h(u)\cap (F+G)^{-1}(0)$, where $F : K \to H$ is $\alpha$-inverse strongly monotone, $G$ is maximal monotone operator on $H$, $h : K \to (-\infty, +\infty]$ is convex lower semi-continuous and $T : K \to K$ is a $b$-contraction mappings. The method is given by

where $J^{G}_{\theta_{n}} = (I-\theta_{n}G)^{-1}$. Additionally, the $x_n$ sequence created by this method, converges to a common solution.

In 2014, the modified variational inclusion problem (MVIP) was first proposed by Khuangsatung and Kangtunyakarn ^[20]. The problem is determining $x$ in $H$, thus

where $i = 1, 2, ..., N, a_{i}\in (0, 1)$ with the condition $\sum_{i = 1}^{N}a_{i} = 1,$ $F_i : H \to H$ is $a_i$-inverse strongly monotone and $G : H \to 2^H$ maximal monotone mappings. Reduce from the problem (1.4) to the problem (1.2) if $F_{i}\equiv F$ for all $i = 1, 2, ..., N$. Moreover, they proved a strong convergence theorem for finding a common element of the set of fixed points of a $\kappa$-strictly pseudononspreading mapping and the set of solutions of a finite family of variational inclusion problems and the set of solutions of a finite family of equilibrium problems in Hilbert space. Afterwards, Khuangsatung and Kangtunyakarn ^[21] introduced the iterative method for solving a finite family of nonexpansive mappings of fixed point $T$ and a finite family of variational inclusion problems in Hilbert spaces under the condition $\sum_{i = 1}^{n}a_{i} = \sum_{i = 1}^{n}\delta_{i} = 1.$ Their method is given by the following:

Furthermore, they only demonstrated that the generated $x_n$ strongly converges to a common element of the common problems.

Motivated by the idea of ^[19,20,21], we establish a modified proximal point algorithm to solve a common problem between the convex constrained optimization problem and the modified variational inclusion problem by combining the algorithm of ^[19,21] and using the condition $\sum_{i = 1}^{N}a_{i} = 1$. Under appropriate conditions, the strong convergence theorem is presented in Hilbert spaces. Eventually, the proposed algorithm is applied to image restoration problems. Image restoration is an important problem in high-level image processing. During data collection, images usually suffer degradation. Blurring, information loss due to sampling, quantization effects, and different noise sources can all be a part of the degradation. The goal of image restoration is to estimate the original image from degraded data. So, the proposed algorithm could be used to solve image restoration problems where the images have suffered a variety of blurring operations. We also compare the image quality by using the signal-to-noise ratio (SNR). In numerical experiments, it was shown that the proposed algorithm is better than Khuangsatung and Kangtunyakarn's method when applied to image restoration.

The following is a summary of the work's content: basic lemmas and definitions are compiled in Section 2. Our algorithm is presented in detail in Section 3. In Section 4, there is a discussion of the numerical experiments. In the last section, this work's conclusion is given.

2.   Preliminaries

We provide certain introductions, definitions, and lemmas in this part that are used in the main result section. Suppose that $F$ is nonlinear with a single-valued of $K$ into $H$. If $F$ is $\alpha$-inverse strongly monotone, then there exists $\alpha > 0$, $\langle Fx - Fy, x - y\rangle \geq \alpha\|Fx - Fy\|^2$ for every $x, y \in K.$ Obviously, $F$ is a monotone Lipschitz continuous if $\alpha$-inverse strongly monotonous. In this paper, we assume that $G : H \to 2^H$, $h : K \to (-\infty, +\infty]$ and $T : K \to K$.

Lemma 1. ^[22] Assume that $F$ is an $\alpha$-inverse strongly monotone mapping on $H$. Then $I-\theta F$ is nonexpansive for every $x, y\, \in H$ and $\theta \in [0, 2\alpha].$

Lemma 2. ^[23] Let $T$ be a proper lower semicontinuous. The inequality

and $\lambda > 0$ holds.

$J^G_\lambda$ is a resolvent operator that is determined by: $J^G_\lambda x = (I+\lambda G)^{-1}(x),$ for every $x$ in $H$ when $\lambda > 0$ and $G$ is the maximal monotone. The operator $J^G_\lambda$ has 1-inverse strongly monotone and single-valued nonexpansive properties. Obviously, a VIP solution is an operator $J^G_\lambda(I - \lambda F$) fixed point, every $\lambda > 0$ (see ^[24]).

The definition of the Moreau-Yosida resolvent $f$ is

for every $x\in H, \lambda > 0.$ The set of minimizers of $f$ corresponds with the collection of the resolvent's fixed points that are associated to $F$, as seen in ^[4]. Subsequently, the resolvent $J^f_\lambda$ is nonexpansive.

Lemma 3. ^[25] Suppose that $T$ is a proper lower semicontinuous. For every $\mu > 0$ and $r > 0$, thus

holds.

When discussing fixed point iterative algorithm convergence, the demiclosedness of a nonlinear operator $\varGamma$ is often discussed correctly.

Lemma 4. ^[26] Suppose that $\varGamma$ is nonexpansive and $Fix(\varGamma) \neq \emptyset.$ Then $I-\varGamma$ is demiclosed. Therefore $\{x_n\}$ converges to $x$ and $(I-\varGamma)x_n$ converges to $y$. Thus $(I-\varGamma)x = y$.

Lemma 5. ^[11] Suppose that $F$ is a monotone Lipschitz continuous and $G$ is a maximal monotone mapping on $H$. Then, the mapping $G + F$ is maximal monotone.

Lemma 6. ^[27] The following statements are hold:

(i) $\forall$ $u, v \in H, \quad \|u\|^{2} -\|v\|^{2} - 2\langle u- v, v \rangle \geq \|u- v\|^{2}$;

(ii) $\forall$ $u, v \in H, \quad \|u+v\|^{2}\leq\|u\|^{2}+2\langle v, u+ v\rangle$;

(iii) $\forall$ $\alpha, \beta \in [0, 1]$ with $\alpha +\beta = 1,$

$\quad\quad\, \, \, \|\alpha u + \beta v \|^{2} = \alpha\|u\|^{2}+\beta\|v\|^{2}-\alpha\beta\| u - v \|^{2}.$

Lemma 7. ^[28] Suppose that $\{\beta_n\} > 0$ and $\beta_n+1 \leq (1 - \epsilon_n)\beta_n + \gamma_n$ for every $n \geq 0, \{\gamma_n\} \in (-\infty, \infty)$ and $\{\epsilon_n\} \in (0, 1)$ such that

(i) $\sum\limits_{n = 0}^{\infty}\epsilon_n = \infty$,

(ii) $\limsup\limits_{n\to\infty}\frac{\gamma_n}{\epsilon_n}\leq0\; \; or\; \; \sum\limits_{n = 0}^{\infty}|\gamma_n| < \infty.$

Then, $\lim\limits_{n\to\infty}\beta_n = 0.$

3.   Results

In order to find a common element between convex minimization and the solutions of MVIP, we will analyze and collect information on a proposed proximal iterative technique hiring inverse strongly monotone and maximal monotone mapping. For the purposes of this investigation, assume that the following assumptions are acceptable.

Assumption

(A1) $T$ is a $b$-contraction mapping on $K$ and $h : K \to (-\infty, +\infty]$ is convex and proper lower semicontinuous function.

(A2) $F_i : K \to H$ is an $\alpha_i$-inverse strongly monotone for every $i$ and $G : K \to 2^H$ is a maximal monotone operator.

(A3) $\Omega : = \arg\min_{u\in K} h(u)\cap(\sum\limits_{n = 1}^{N} \delta_i F_i+G)^{-1}(0) \neq \emptyset.$

Algorithm 1. Choose $x_0 \in K$ and $\{\alpha_n\}, \{\lambda_n\}, \{\theta_n\} \in (0, 1$) and $\lambda_n \geq \lambda > 0.$

Step 1. Put $u_n$ as

Step 2. Compute

Set n = n + 1, and go back to Step 1.

Lemma 8. Algorithm 1 generates a bounded sequence $\{x_n\}$.

Proof. In $\Omega$, only exists one solution to the variational inequality because $(I-T)$ and $\Omega$ have the property of being closed convex. $z$ refers the one and only solution to the variational inequality problem. For every $u\in K$, $h(z)\leq h(u)$ according to the equality (3.9) and the properties of $h$, so

From the Moreau-Yosida resolvent definition, we obtain that $J^h_{\lambda_n} z = z$. This implies that

By (3.9), Lemma 1 and $z = J^G_{\theta_n}(I -\theta_n \sum_{n = 1}^{N} \delta_i F_i)z$, we see that

for every $n\geq 0.$ It can conclude

Using the induction on $n$, it can deduce that

Hence $\{x_n\}$ is bounded.

Theorem 1. Assume that

(i) $\lim\limits_{n\to\infty}\alpha_n = 0$ and $\sum\limits_{n = 0}^{\infty}\alpha_n = \infty$,

(ii) $\theta_n \in [a, b] \subset (0, \min\{1, 2\alpha\})$, and

(iii) $\sum\limits_{n = 1}^{N} \delta_i = 1.$

Then Algorithm 1 generates a sequence $\{x_{n}\}$ that converges to $z \in \Omega$. That is,

Proof. We shall take into consideration two cases for the proof.

Case 1. Assume that there is $n_0 \in\mathbb{N}.$ Then $\{\|x_n-x^*\|\}$ is decreasing, every $n \geq n_0.$ Denote that $\{\|x_n-x^*\|\}$ is monotone and bounded, it can imply that $\{\|x_n-x^*\|\}$ is convergent. Thus

By Lemma 2 and $h(z) \leq h(u_n)$,

By inequality (3.9), (3.5) and the propoty of $\|.\|^2,$ it obtains

That is,

Thus, $(1-\alpha_n)\|x_n-u_n\|^2\leq\|x_n-z\|^2-\|x_{n+1}-z\|^2+\alpha_n\|T(x_n)-z\|^2.$ From (3.4) and $\alpha_n \to 0$, so $\lim\limits_{n\to\infty}\|x_n-u_n\|^2 = 0.$ Using (3.9) and Lemma 1,

Therefore,

According to $\{\alpha_n\}$ converges to $0$, (3.4), and $\{x_n\}$ is bounded, it obtains that

Since (3.9) and $J^G_{\theta_n}$ is 1-inverse strongly monotone, we get

It implies

Therefore

By the definition of $x_n$,

Consider

Hence

Since $\alpha_n \to 0$ as $n \to \infty,$ inequality (3.4) and (3.6), we have

We demonstrate $\limsup\limits_{n\to+\infty}\langle z-T(z), z-x_n\rangle\leq0$. Because $\{x_n\}$ is bounded, a subsequence $\{x_{n_k}\}$ exists that weakly converges to $x^* \in K$. Thus $\limsup\limits_{n\to+\infty}\langle z-T(z), z-x_n\rangle = \lim\limits_{k\to+\infty}\langle z-T(z), z-x_{n_k}\rangle.$ From Lemma 3 and (3.9), we see that

Hence,

By using (3.8), Lemma 4 and $J^h_{\lambda}$ is nonexpansive, we have $x^* \in Fix(J^h_{\lambda}) = \arg\min_{u\in k}h(u)$. Now, we will show $x^* \in (\sum_{n = 1}^{N} \delta_i F_i + G)^{-1}(0).$ By Lemma 5, $G + F_i$ is maximal monotone. Let $(v, u) \in M(G+\sum_{n = 1}^{N} \delta_i F_i).$ That is, $u - \sum_{n = 1}^{N} \delta_i F_iv \in G(v).$ We set $z_n : = J^G_{\theta_n}(u_n - \theta_n\sum_{n = 1}^{N} \delta_i F_iu_n).$ Since $z_{n_k} = J^G_{\theta_{n_k}}(u_{n_k} - \theta_{n_k}\sum_{n = 1}^{N}\delta_i F_iu_{n_k}),$ we have $u_{n_k}-\theta_{n_k}u_{n_k} \in (I + \theta_{n_k}G)z_{n_k}, i.e., \frac{1}{\theta_{n_k}}(u_{n_k} -z_{n_k}-\theta_{n_k}\sum_{n = 1}^{N} \delta_i F_iu_{n_k}) \in G(z_{n_k}).$ By maximal monotonicity of $G + F_i,$ we obtain

Then

Hence

From $\|z_n-u_n\| \to 0, \|\sum_{n = 1}^{N} \delta_i F_iz_n-\sum_{n = 1}^{N} \delta_i F_iu_n\| \to 0$ and $z_{n_k} \rightharpoonup x^*,$ we obtain

and $x^* \in \big(\sum_{n = 1}^{N} \delta_i F_i+G\big)^{-1}(0).$ Therefore, $x^* \in \big(\sum_{n = 1}^{N} \delta_i F_i+G\big)^{-1}(0) \cap \arg\min u_{u\in k}h(u).$ The fact that $z$ solves (3.3), we get

Eventually, we will show that $x_n \to z.$ By using Lemma 6 and (3.9),

Consider

Therefore $x_n\to z.$

Case 2. There is no eventual decrease in the sequence $\{\|x_n-z\|\}.$ Put

Assume that $\zeta$ is a mapping on $\mathbb{N}$ for every $n \geq n_0$. We denote that

So $\zeta(n) \to \infty$ and $\Upsilon_{\zeta(n)} \leq \Upsilon_{\zeta(n)+1}$ for $n \geq n_0$. Case 1 can demonstrate that

and $\{x_{\zeta(n)}\}_{n\geq 1}$ is bounded. For every $n \geq n_0$,

Thus $2\alpha_{\zeta(n)}\langle z-T(z), z-x_{\zeta(n)+1}\rangle \geq a_{\zeta(n)}(1-b)\|x_{\zeta(n)}-z\|^2.$ Therefore

It obtains that $\lim\limits_{n\to\infty}\|x_{\zeta(n)}-z\|^2 = 0.$ Hence $\lim\limits_{n\to\infty}\Upsilon_{\zeta(n)} = \lim\limits_{n\to\infty}\Upsilon_{\zeta(n)+1} = 0.$ For $n \geq n_0,$ it obtains $\Upsilon_{\zeta(n)} \leq \Upsilon_{\zeta(n)+1}.$ For $\zeta(n) + 1 \leq j \leq n, \, \Upsilon_j > \Upsilon_{j+1}.$ Then $n > \zeta(n).$ In particular, for every $n \geq n_0$, $\max \{\Upsilon_{\zeta(n)}, \Upsilon_{\zeta(n)+1}\} = \Upsilon_{\zeta(n)+1}\geq \Upsilon_{n} \geq 0.$ Thus $0\leq\lim\limits_{n\to\infty}\Upsilon_n\leq\lim\limits_{n\to\infty}\Upsilon_{\zeta(n)+1} = 0.$ Hence, $\lim\limits_{n\to\infty}\Upsilon_n = \lim\limits_{n\to\infty} \|x_n-z\|^2 = 0.$ Thus $\{x_n\}$ strongly converges to $z.$

When setting $F_{i}\equiv F$ in Algorithm 1, it can obtain the following corollary.

Corollary 1. ^[19] Let $K$ be a nonempty closed convex subset of a real Hilbert space $H$. Let $h : K \to (-\infty, +\infty]$ be a proper, lower semi-continuous and convex function and $F$ be an $\alpha$-inverse strongly monotone operator of $K$ into $H$. Let $T : K \to K$ be a $b$-contraction mapping and $G$ be a maximal monotone operator on $H$ such that $\varGamma : = argmin_{u\in K} h(u)\cap(F+G)^{-1}(0)$ is non-empty and the domain of $G$ is included in $K$. Let $\{x_n\}$ be a sequence defined as follows:

where $\{\alpha_n\}, \{\lambda_n\}$ and $\{\theta_n\}$ be sequences in $(0, 1$) and $\lambda_n \geq \lambda > 0$ for all $n \geq 1$ and some $\lambda$ satisfying the following conditions:

(i) $\lim\limits_{n\to\infty}\alpha_n = 0$ and $\sum\limits_{n = 0}^{\infty}\alpha_n = \infty$.

(ii) $\theta_n \in [a, b] \subset (0, min\{1, 2\alpha\})$.

Then, the sequence $\{x_n\}$ generated by (3.9) converges strongly to $p \in \varGamma$, which is the unique solution of the variational inequality problem:

4.   Numerical experiments

Image restoration is to repair or eliminate noise or damaged images that degrade an image. There are numerous types of deterioration, such as torn, blurred, noisy, out of focus, dirty, scratched, etc. Neither the occasional falling of liquids such as water nor the desire to preserve our ancient images or something similar. By utilizing the actual blurring function, we are able to estimate motion blur. And remove the blur to create an original and realistic image.

Therefore, the researcher is interested in denoising and deblurring images for this section. It is well known that by inverting the following observation model, the general problem of image restoration can be described by

where $\textbf{H}\in\mathbb{R}^{m\times n}$ is the blurring operation, $b$ is additive noise, $w\in\mathbb{R}^{m}$ is the observed image and $x\in \mathbb{R}^{n}$ is an original image. This problem basically relates to the various formulations for optimization methods that are available. The goal in image restoration is to deblur an image without knowing which one is the blurring operator. Thus, we focus on the following problem:

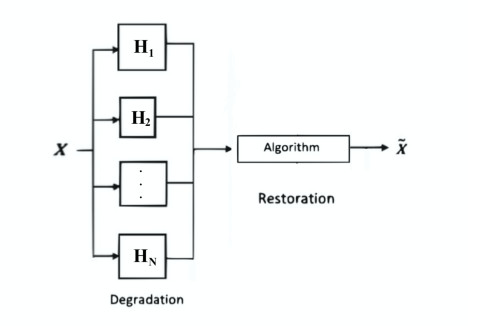
where $\|x\|_1 = \sum_i|x_i|$, $\kappa$ is a parameter that is relate to noise $b$, $w_i$ is the blurred image as determined by the blurred matrix $\textbf{H}_i$ for every $i = 1, 2, ..., N$ and $x$ is the original image. Suppose that $f_i(x) = \frac{1}{2}\|w_i-\textbf{H}_ix\|^2$ and $g = \kappa\|x\|_1$, the Lipschitz gradient of $f_{i}$ is $\bigtriangledown f_{i}(x) = \textbf{H}_i^T(\textbf{H}_ix-w_i)$. For solving the problem (4.2), we designed the following flowchart (Figure 1). Where $\tilde{X}$ is the deblurred image or the common solutions of the problem (4.2) and as seen in Figure 1. We can apply the algorithm in Theorem 1 to solve the problem (4.2) by setting $F_{i} = \bigtriangledown f_{i}$ and $G = \partial g$.

For the purpose of this experiment, we will apply our suggested algorithm to resolve the problem (4.2), which entails recovering an original image $x\in\mathbb{R}^{n}$. In terms of the image's signal-to-noise ratio (SNR),

we compare our proposed algorithm to one developed by Khuangsatung and Kangtunyakarn ^[20], which also holds strong convergence. A higher SNR indicates a higher recovery quality. Let $N = 4$. Consider a simple linearized image recovery model $\textbf{H}_ix = \rho_i*x$, where a motion orientation $11^\circ\; (\theta = 11)$, $\rho_1$ is a motion blur with a 21-pixel motion length (len = 21), $\rho_2$ is a filter size $9 \times 9$ Gaussian blur with a $\sigma = 2$ standard deviation, $\rho_3$ is a circular averaging filter with radius $r = 4$, and $\rho_4$ is an averaging blur of filter size $9\times 9$. The following values are set for all of the parameters: $\alpha_n = \frac{1}{2n+2}, \theta_n = 0.1, \lambda_n = 0.5, \kappa = 0.01$, $\delta_n = 0.25$, and $f(x) = \frac{x}{100}$. The numerical results from the experiment are shown in the following: Figure 2 depicts the original grayscale images. Figures 3 and 4 illustrate greyscale images degraded by matrix blurs $\rho_1$ through $\rho_4$. Figures 5 and 6 show the grayscale images result by Arunchai and by Khuangsatung. Figures 7 and 8 depict the SNR result of Arunchai is higher than Khuangsatung.

Remark 1. Experimentally, It was determined that the problem (4.2) could be resolved using our algorithm, and that they are preferable to algorithms developed previously. Our algorithm appears to be more effective at solving these types of problems. This is supported by the SNR values.

5.   Conclusions

The problems of modified variational inclusion and variational inclusion are solved using a modified proximal point algorithm. Additionally, we have used the suggested algorithm to solve the many degradations in image restoration.

Acknowledgments

The authors would like to thank King Mongkut's University of Technology North Bangkok (KMUTNB), Rajamangala University of Technology Thanyaburi (RMUTT) and Nakhon Sawan Rajabhat University. This research was funded by National Science, Research and Innovation Fund (NSRF), King Mongkut's University of Technology North Bangkok with Contract No. KMUTNB-FF-65-13.

Conflict of interest

The authors declare no conflict of interest.