On the exponential sums estimates related to Fourier coefficients of $GL_3$ Hecke-Maaß forms

1.   Introduction

We initiate our study by the conception of concavity of functions which is stated as follows: Any function ${\mathcal{E}}:[{{\sigma_{1}}}, {\delta_{1}}]\rightarrow \mathbb{R}$ is referred to as a convex function if,

where ${\kappa}\in[0, 1]$. Due to the several important geometrical and analytical aspects, convex functions are discussed from multiple approaches and directions in the literature. They have an immense amount of applications and generalizations to investigate non-convex problems. Their role in the emergence of inequalities is unprecedented because this concept itself is closely linked with inequalities. One can easily relate the that almost fundamental results in the theory of inequalities having a governing role can be achieved directly or indirectly by considering the convex functions. Now we provide a significant consequence of convex functions:

Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}$ be a convex function. Then,

From this inequality, one can conclude that this result computes the bounds for the average mean value integral of convex functions. Moreover, this result serves as a criteria to discuss the concavity of functions. Also, this result has several applications in the theory of means, special functions, error analysis probability theory, information theory, etc. Due to the effective range of implications, several variants of trapezium-type inequalities have been developed and assessed through various classes of convex functions along with applications. For recent developments, consult ^{[1,2,3,4,5,6]}.

Furthermore, we recover the essential prelude relative to interval analysis to attain the required result. Suppose that the space of all non-empty compact intervals and positive non-degenerate compact intervals of the real line $\mathbb{R}$ are specified by $\mathbb{R}_{I}$ and $\mathbb{R}_{I}^+$. For any ${\mathcal{A}}, {\mathcal{A}}_{2}\in \mathbb{R}_{I}$ such that ${{\mathcal{A}}_{1}} = [{\sigma_{1}}_{\star}, \, {\sigma_{1}}^{\star}]$ and ${\mathcal{A}}_{2} = [{\delta_{1}}_{\star}, \, {\delta_{1}}^{\star}]$ and $\lambda\in\mathbb{R}$, then

and

The concept of generalized Hukuhara(gh) difference was developed in ^[7].

Let ${\mathcal{A}_{1}}, {\mathcal{A}}_{2}\in \mathbb{R}_{I}$. The $gh$ difference is illustrated as:

Also, for ${\mathcal{A}_{1}}\in \mathbb{R}_{I}$, the length of interval is computed by $w({\mathcal{A}}_{1}) = {\sigma_{1}}^{\star}-{\sigma_{1}}_{\star}$. Then, for all ${\mathcal{A}_{1}}, {\mathcal{A}}_{2}\in \mathbb{R}_{I}$, we have

Some properties linked with the $gH$-difference are described as follows:

(1) ${\mathcal{A}_{1}}\ominus_{g} {\mathcal{A}_{1}} = \{0\}, \quad {\mathcal{A}_{1}}\ominus_{g}\{0\} = {\mathcal{A}_{1}}, \quad \{0\}\ominus_{g}{\mathcal{A}_{1}} = -{\mathcal{A}_{1}}$,

(2) ${\mathcal{A}_{1}}\ominus_{g} {\mathcal{A}}_{2} = (-{\mathcal{A}}_{2})\ominus_{g}(-{\mathcal{A}_{1}}) = -({\mathcal{A}}_{2}\ominus_{g}{\mathcal{A}_{1}})$,

(3) ${\mathcal{A}_{1}}\ominus_{g}(-{\mathcal{A}}_{2}) = {\mathcal{A}}_{2}\ominus_{g}(-{\mathcal{A}_{1}}) = -({\mathcal{A}}_{2}\ominus_{g}{\mathcal{A}_{1}})$,

(4) $({\mathcal{A}_{1}}+{\mathcal{A}}_{2})\ominus_{g}{{\mathcal{A}}_{2}} = {\mathcal{A}_{1}},$

(5) $\lambda {\mathcal{A}_{1}}\ominus_{g}\lambda {{\mathcal{A}}_{2}} = \lambda({\mathcal{A}_{1}}\ominus_{g}{{\mathcal{A}}_{2}})$.

For any ${\mathcal{A}_{1}}, {{\mathcal{A}}_{2}}, C, D\in\mathbb{R}_{I}$, consider ${\kappa}_{1} = w({\mathcal{A}_{1}})-w(C), \quad {\kappa}_{2} = w({\mathcal{A}}_{2})-w(D), \quad {\kappa}_{3} = w({\mathcal{A}_{1}})-w({\mathcal{A}}_{2})$, and ${\kappa}_{4} = w(C)-w(D)$. Then:

(1) $({\mathcal{A}_{1}}+{\mathcal{A}}_{2}){\ominus_{g}}(C+D) = \left\{ \begin{array}{ll} \, ({\mathcal{A}_{1}}\ominus_{g}C)+({\mathcal{A}}_{2}\ominus_{g}D), \quad {\kappa}_{1}{\kappa}_{2}\geq0, \\ \, ({\mathcal{A}_{1}}\ominus_{g}C)\ominus_{g}(-{\mathcal{A}}_{2}\ominus_{g}D), {\kappa}_{1}{\kappa}_{2} < 0. \end{array} \right.$

(2) $({\mathcal{A}_{1}}\ominus_{g}{\mathcal{A}}_{2})+(C\ominus_{g}D) = \left\{ \begin{array}{ll} \, ({\mathcal{A}_{1}}\ominus_{g}(-C)){\ominus_{g}}({\mathcal{A}}_{2}\ominus_{g}(-D)), {\kappa}_{1}{\kappa}_{2}\geq0, {\kappa}_{3}{\kappa}_{4} < 0, \\ \, ({\mathcal{A}_{1}}\ominus_{g}(-C))+(-{\mathcal{A}}_{2}\ominus_{g}D), \; \; {\kappa}_{1}{\kappa}_{2} < 0, {\kappa}_{3}{\kappa}_{4} < 0, \\ \, ({\mathcal{A}_{1}}+C)\ominus_{g}({\mathcal{A}}_{2}+D), \quad\quad\quad {\kappa}_{3}{\kappa}_{4}\geq0. \end{array} \right.$

(3) $({\mathcal{A}_{1}}\ominus_{g}{\mathcal{A}}_{2})\ominus_{g}(C\ominus_{g}D) = \left\{ \begin{array}{ll} \, ({\mathcal{A}_{1}}\ominus_{g}C){\ominus_{g}}({\mathcal{A}}_{2}\ominus_{g}D), \quad \quad\; {\kappa}_{1}{\kappa}_{2}\geq0, {\kappa}_{3}{\kappa}_{4}\geq0, \\ \, ({\mathcal{A}_{1}}\ominus_{g}C)+(-({\mathcal{A}}_{2}\ominus_{g}D)), \; \; \; \; {\kappa}_{1}{\kappa}_{2} < 0, {\kappa}_{3}{\kappa}_{4}\geq0, \\ \, ({\mathcal{A}_{1}}+(-C))\ominus_{g}({\mathcal{A}}_{2}+(-D)), {\kappa}_{3}{\kappa}_{4} < 0. \end{array} \right.$

Any function $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ is regarded as an $\mathcal{I}.\mathcal{V}$ function if $\mathcal{E}({\varrho}) = [\mathcal{E}_{\star}({\varrho}), \mathcal{E}^{\star}({\varrho})]$ such that $\mathcal{E}_{\star}({\varrho})\leq \mathcal{E}^{\star}({\varrho}), \forall {\varrho} \in [{\sigma_{1}}, {\delta_{1}}]$. It is crucial to understand that $\lim_{{\varrho}\rightarrow {{\varrho}_{0}}} \mathcal{E}({\varrho})$ exist $\Leftrightarrow$ $\lim_{{\varrho}\rightarrow {{\varrho}_{0}}}\mathcal{E}_{\star}({\varrho})$ and $\lim_{{\varrho}\rightarrow {{\varrho}_{0}}}\mathcal{E}^{\star}({\varrho})$.

Additionally, an $\mathcal{I}.\mathcal{V}$ function $\mathcal{E}$ is assumed to be continuous $\Leftrightarrow$ both $\mathcal{E}_{\star}$ and $\mathcal{E}^{\star}$ are continuous. Presume that $\mathcal{E}, g:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$. Then, $(\mathcal{E}\ominus_{g}g)({\varrho}) = \mathcal{E}({\varrho})\ominus_{g}g({\varrho}):[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$, and

exists, if $\lim_{{\varrho}\rightarrow {\varrho}_{0}}\mathcal{E}({\varrho}) = A$ and $\lim_{{\varrho}\rightarrow {\varrho}_{0}}g({\varrho}) = {\delta_{1}}$.

One can notice that if $\mathcal{E}, g:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ obey the continuous property of functions, then $\mathcal{E}\ominus_{g}g$ is referred to as a continuous function.

Consequently, we come up with differentiability concepts based on the $\ominus_{g}$ difference.

Definition 1.1. Presume that $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}$ is an $\mathcal{I}.\mathcal{V}$ function. Then,

is termed as $\ominus_{g}$ derivative at ${\varrho}\in[{\sigma_{1}}, {\delta_{1}}]$. $\mathcal{E}$ is differentiable on $({\sigma_{1}}, {\delta_{1}})$ if it is differentiable almost everywhere in the domain.

Now, we discuss the concept of $\mathcal{I}.\mathcal{V}$ convex functions.

Definition 1.2. Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}$ be an $\mathcal{I}.\mathcal{V}$ function satisfying $\mathcal{E}({\varrho}) = [\mathcal{E}_{\star}({\varrho}), \, \mathcal{E}^{\star}({\varrho})]$. Then, it is considered as an $\mathcal{I}.\mathcal{V}$ convex, if

The next result ensures the convexity of functions in the interval domain.

Theorem 1.1. Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}$ be an $\mathcal{I}.\mathcal{V}$ function such that $\mathcal{E}({\varrho}) = [\mathcal{E}_{\star}({\varrho}), \, \mathcal{E}^{\star}({\varrho})]$. Then, $\mathcal{E}$ is an $\mathcal{I}.\mathcal{V}$ convex function $\Leftrightarrow$ $\mathcal{E}_{\star}$ is a convex function and $\mathcal{E}^{\star}$ is a concave function.

The $\mathcal{I}.\mathcal{V}$ analogues of the trapezium inequality through containments ordering relation is given as follows:

Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}^{+}$ be an $\mathcal{I}.\mathcal{V}$ convex function. Then,

For, comprehensive review, see ^[8].

${\mathtt{q}}$-Symmetric Calculus. Throughout the investigation, let $I = [{\sigma_{1}}, {\delta_{1}}]$ be any arbitrary subset of $\mathbb{R}$ such that $0\in I$ and ${\mathtt{q}}\in(0, 1)$. Then, the ${\mathtt{q}}$-geometric set is expressed as $I_{{\mathtt{q}}} = \{{\mathtt{q}}{\varrho}|{\varrho}\in I\}$. Taking the benefit of this set, the classical symmetric quantum difference operator and left and right quantum symmetric derivatives are defined as follows:

Definition 1.3 (^[9]). Let $\mathcal{E}:I\rightarrow \mathbb{R}$. Then the symmetric quantum variant derivative operator is

And, $D_{{\mathtt{q}}}^{s}\mathcal{E}(0) = \mathcal{E}'(0)$, where ${\kappa} = 0$ provided that $\mathcal{E}$ is differentiable at ${\kappa} = 0$. If $\mathcal{E}$ is a differentiable function at ${\kappa}\in I_{{\mathtt{q}}}$, then $\lim_{{\mathtt{q}}\rightarrow 1}D_{{\mathtt{q}}}^{s}\mathcal{E}({\kappa}) = \mathcal{E}'({\kappa})$.

The quantum symmetric number is described as

Recently, Bilal et al. ^[10] proposed the conception of quantum symmetric operators over finite intervals. Presume that $I = [{\sigma_{1}}, {\delta_{1}}]\subset \mathbb{R}$, $0\in I$ and $0 < {\mathtt{q}} < 1$. Then the left sided quantum symmetric derivative is given as

Definition 1.4 (^[10]). Presume that $\mathcal{E}:J\rightarrow \mathbb{R}$ is a continuous function. Then

And, ${_{{{\sigma_{1}}}}D_{{\mathtt{q}}}^{s}}\mathcal{E}({{\sigma_{1}}}) = \lim_{{\mathtt{q}}\rightarrow 1}{_{{{\sigma_{1}}}}D_{{\mathtt{q}}}^{s}}\mathcal{E}({\kappa})$, if the limit exists. If ${{\sigma_{1}}} = 0$, then ${_{{{\sigma_{1}}}}D_{{\mathtt{q}}}^{s}}\mathcal{E} = {D_{{\mathtt{q}}}^{s}}\mathcal{E}$.

Consequently, the corresponding integral operator is stated as

Definition 1.5. Presume that $\mathcal{E}:J\rightarrow \mathbb{R}$ is a continuous function. Then

If ${{\sigma_{1}}} = 0$, then it coincides with the symmetric quantum integrals operator in ^[9]. For more detail concerning quantum symmetric differences, see ^[11].

Definition 1.6 (^[12]). Let $\mathcal{E}:I\rightarrow \mathbb{R}$ be a continuous function. Then,

And, ${^{{\delta_{1}}}D_{{\mathtt{q}}}^{s}}\mathcal{E}({\delta_{1}}) = \lim_{{\mathtt{q}}\rightarrow 1}{^{{\delta_{1}}}D_{{\mathtt{q}}}^{s}}\mathcal{E}({\kappa})$, if the limit exists. If ${\delta_{1}} = 0$, then ${^{{\delta_{1}}}D_{{\mathtt{q}}}^{s}}\mathcal{E} = {D_{{\mathtt{q}}}^{s}}\mathcal{E}$.

Definition 1.7 (^[12]). Presume that $\mathcal{E}:I\rightarrow \mathbb{R}$ is a continuous function. Then,

Clearly, a function is said to be right quantum symmetric integrable if $\sum_{n = 0}^{\infty}{\mathtt{q}}^{2n+1}\mathcal{E}({\mathtt{q}}^{2n+1}{\kappa}+(1-{\mathtt{q}}^{2n+1}){\delta_{1}})$ converges. Remember that the above-discussed operators do not coincide with classical Jackson ${\mathtt{q}}$ operators.

Recently, Cortez et al. ^[13] investigated the interval-valued quantum symmetric operators in interval space based on Hukuhara differences, which are described as

Definition 1.8. Suppose $\mathcal{E}:I\rightarrow \mathbb{R}_{I}$ is continuous $\mathcal{I}.\mathcal{V}$ function. Then, the left interval-valued quantum symmetric difference operator is defined as

And the corresponding integral operator is expressed as

Definition 1.9. Let $\mathcal{E}\in C([{\sigma_{1}}, {\delta_{1}}], \mathbb{R}_{I})$. Then the $_{{\sigma_{1}}}I_{{\mathtt{q}}, s}^{i}$-integral operator is described as

One can easily observe that a function is considered to be I.V left ${\mathtt{q}}$-symmetric integrable if $\sum_{n = 0}^{\infty}{\mathtt{q}}^{2n}\mathcal{E}({\mathtt{q}}^{2n+1}{\delta_{1}}+(1-{\mathtt{q}}^{2n+1}){\sigma_{1}})$ converges.

In 2013, Tariboon and Ntouyas ^[14] noticed some limitations of ${\mathtt{q}}$-Jackson operators over finite intervals in impulsive difference equations and developed the ${\mathtt{q}}$ operators over finite interval connected with left point and explored its several implications in both impulsive difference equations and inequalities as well. This development paved another way to investigate integral inequalities. Alp and his coauthors ^[15] noticed that the trapezoidal inequality established in ^[16] is not correct and provided the new proof by using the concept of the support line of differentiable convex functions, and also established several midpoint quantum estimates. The authors of ^[17] analyzed the error estimates of the Milne rule by utilizing the Jensen-Mercer inequality and quantum calculus along with applications. Nosheen et al. ^[18] concluded some new quantum symmetric counterparts of basic inequality results, such as Hölder's inequality and error inequalities of one point rule associated with $s$-convex functions. To prove the Hermite-Hadamard inequality analytically, it was necessary to introduce the right quantum operators. In 2022, Kunt et al. ^[19] introduced the right sided quantum operators and provided their applications in integral inequalities. For a complete investigation, see ^{[20,21,22,23,24,25,26,27]}.

In ^[28,29] the authors computed the estimates of one one-point integration rule incorporated with $\mathcal{I}.\mathcal{V}$ functions and delivered applications as well. Following the idea of the previously discussed paper, Costa and Roman Flores ^[30] computed several fuzzy integral inequalities. In 2018, Zhao et al. ^[31,32] delivered the Jensen's and trapezium type inequalities associated with $\mathcal{I}.\mathcal{V}$-$h$-convex functions and $\mathcal{I}.\mathcal{V}$ Chebyshev kinds of inequalities, respectively. Budak et al. ^[33] initiated the development of fractional versions of the trapezium inequalities for $\mathcal{I}.\mathcal{V}$ convex functions defined by the means of containment ordering. In ^[34] the authors presented the class of $\mathcal{I}.\mathcal{V}$ two-dimensional harmonic convex functions and derived several fractional integral inequalities by taking into account Raina's integral operators. Lou et al. ^[35] devoted their efforts to develop the notion of $\mathcal{I}.\mathcal{V}$ quantum calculus based on generalized Hukuhara differences and provided the applications to inequalities. Motivated by the technique of ^[35], Kalsoom et al.^[36] worked on $\mathcal{I}.\mathcal{V}$ general quantum calculus by the means of Hukuhara differences and explored some applications to the Hermite-Hadamard inequality. Ali et al. ^[37] extended the idea presented in ^[36] for the right $\mathcal{I}.\mathcal{V}$-$(p, {\mathtt{q}})$ operators and presented their key properties. Bin-Mohsin et al. ^[38] stated another class of generalized convexity based on a left-right ordering relation named as LR-fuzzy bi-convex function, and delivered Hermite-Hadamard and its weighted forms type results. In 2022, Duo and Zhou ^[39] examined the coordinated integral inequalities by considering the two-dimensional convex functions generalized integral operator having a non-singular kernel. In ^[40] the authors reported the parametric fractional versions of inequalities through convex functions and presented some visuals to support their outcomes.

The principal intent of this article is to examine the right sided quantum symmetric operators in the frame work of $\mathcal{I}.\mathcal{V}$ functions along with their implications. We structured our study into two portions: In the initial portion of the study, we recover some vital details, background, and inspiration of the research. In the next part, we introduce the $\mathcal{I}.\mathcal{V}$ right symmetric quantum derivative operators based on generalized Hukuhara difference and discuss their key properties. Based on the newly developed quantum operators, a new antiderivative operator is developed. Also, some crucial results, including the fundamental theorem of calculus and several other properties will be provided. Later on, several Hermite-Hadamard-type inequalities will be proved by both graphical and analytical methods essentially utilizing the convexity of the function. We will also present a visual breakdown in the support of principal findings.

2.   $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric operators

In the current part of the study, interval-valued quantum symmetric operators are based on $\ominus_{g}$ differences. First, we introduce the notion of interval-valued right symmetric quantum difference and integral operators and their properties.

2.1.   $^{{\delta_{1}}}d_{{\mathtt{q}}, s}^{i}$-operator and its properties

Now, we investigate the right $\mathcal{I}.\mathcal{V}$ ${\mathtt{q}}$-symmetric difference and integral operators and their properties. The space of left ${\mathtt{q}}$-symmetric differentiable operators is denoted by $^{{\delta_{1}}}d_{{\mathtt{q}}, s}^{i}$.

Definition 2.1. Suppose $\mathcal{E}:I\rightarrow \mathbb{R}_{I}$ is a continuous $\mathcal{I}.\mathcal{V}$ function. Then, the right $\mathcal{I}.\mathcal{V}$ ${\mathtt{q}}$-symmetric difference operator is defined as

Example 2.1. Assume that $\mathcal{E}:[0, 1]\rightarrow \mathbb{R}_{I}$ is an $\mathcal{I}.\mathcal{V}$ function such that $\mathcal{E}({\varrho}) = [-4{\varrho}, 5{\varrho}]$. Then, we compute ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho})$ by implementing Definition 2.1, and we have

Theorem 2.1. A function $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ is $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable at ${\varrho}\in[{\sigma_{1}}, {\delta_{1}}]$ $\Leftrightarrow$ $\mathcal{E}_{\star}$ and $\mathcal{E}^{\star}$ are right quantum symmetric differentiable at ${\varrho}\in[{\sigma_{1}}, {\delta_{1}}]$, and

Proof. Assume that $\mathcal{E}$ is an $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function. Then, there exists $g_{\star}$ and $g^{\star}$ such that ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho}) = [g_{\star}, \, g^{\star}]$, and by considering Definition 1.8, we that

and

exist. Then, ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})$ and ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})$ exist, and (2.1) is straight forward.

Conversely, suppose $\mathcal{E}_{\star}$ and $\mathcal{E}^{\star}$ are right ${\mathtt{q}}$-symmetric differentiable at ${\varrho}$. If ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})$, then

Similarly, if ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})$, then ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho}) = [{^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho}), \, {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})]$. □

Now we provide another characterization of the right ${\mathtt{q}}$-symmetric derivative based on the monotonic property of functions.

Theorem 2.2. Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ and if it is $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable on $[{\sigma_{1}}, {\delta_{1}}]$, then

(1) ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho}) = \left[{^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho}), \, {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})\right]$, if $\mathcal{E}$ is $l$-increasing.

(2) ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho}) = \left[{^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho}), \, {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})\right]$, if $\mathcal{E}$ is $l$-decreasing.

Proof. Suppose that $\mathcal{E}$ is an $l$-increasing and right ${\mathtt{q}}$-symmetric differentiable function on $[{\sigma_{1}}, {\delta_{1}}]$, and we observe that ${\mathtt{q}}^{-1}{\varrho}+(1-{\mathtt{q}}^{-1}){\delta_{1}} > {\mathtt{q}}{\varrho}+(1-{\mathtt{q}}){\delta_{1}}$ for ${\mathtt{q}}\in(0, 1)$. Since $l(\mathcal{E}) = \mathcal{E}^{\star}-\mathcal{E}_{\star}$ is increasing,

Thus,

Hence, the required result is achieved. By a similar process, we can prove the 2nd result. □

Remark 2.1. If ${\upsilon}\in({\sigma_{1}}, {\delta_{1}})$ and $\mathcal{E}$ is $l$-increasing on $[{\sigma_{1}}, {\upsilon})$ and $l$-decreasing on $({\upsilon}, {\delta_{1}}]$, then ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho}) = \left[{^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho}), \, {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})\right]$ on $[{\sigma_{1}}, {\upsilon})$ and ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho}) = \left[{^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho}), \, {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})\right]$ on $({\upsilon}, {\delta_{1}}]$.

Theorem 2.3. Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ be a left symmetric ${\mathtt{q}}$-differentiable function. Then, for any ${\upsilon} = [{\upsilon}_{\star}, {\upsilon}^{\star}]\in\mathbb{R}_{I}$ and $\alpha\in\mathbb{R}$, the mappings $\mathcal{E}+{\upsilon}$ and $\alpha \mathcal{E}$ are also right ${\mathtt{q}}$-symmetric differentiable on $[{\sigma_{1}}, {\delta_{1}}]$. Then:

(1) ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}(\mathcal{E}({\varrho})+{\upsilon}) = {^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho})$.

(2) ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}(\alpha \mathcal{E})({\varrho}) = \alpha {^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho})$.

Proof. For ${\varrho}\in[{\sigma_{1}}, {\delta_{1}}]$ and from Definition 1.8, we have

We leave the second proof for interested readers. □

Theorem 2.4. Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ be a right ${\mathtt{q}}$-symmetric differentiable function. For any ${\upsilon} = [{\upsilon}_{\star}, {\upsilon}^{\star}]\in\mathbb{R}_{I}$, if $l(\mathcal{E})-l({\upsilon})$ has a constant sign over $[{\sigma_{1}}, {\delta_{1}}]$, then $\mathcal{E}\ominus_{g}{\upsilon}$ is right ${\mathtt{q}}$-symmetric differentiable.

Proof. Take ${\varrho}\in[{\sigma_{1}}, {\delta_{1}}]$. Then,

□

Theorem 2.5. Let $\mathcal{E}, g:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}$ be right ${\mathtt{q}}$-symmetric differentiable mappings. Then, the sum $\mathcal{E}+g$ is a right ${\mathtt{q}}$-symmetric differentiable if one of the following cases hold:

(1) If $\mathcal{E}, g$ are equally $l$-monotonic on $[{\sigma_{1}}, {\delta_{1}}]$, then

(2) If $\mathcal{E}, g$ are differently $l$-monotonic on $[{\sigma_{1}}, {\delta_{1}}]$, then

Moreover, in both cases, ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}(\mathcal{E}({\varrho})+g({\varrho}))\subseteq{^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho})+{^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}g({\varrho})$.

Proof. Suppose $\mathcal{E}, g$ are $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable and $l$-increasing on $[{\sigma_{1}}, {\delta_{1}}]$. Then, $\mathcal{E}_{\star}, \mathcal{E}^{\star}, g_{\star}$ and $g^{\star}$ are left ${\mathtt{q}}$-symmetric differentiable, and ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})$, ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}g_{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}g^{\star}({\varrho})$. Then, $\mathcal{E}_{\star}+g_{\star}$ and $\mathcal{E}^{\star}+g^{\star}$ are ${\mathtt{q}}$-symmetric and

By similar proceedings, we can obtain that the result for both $\mathcal{E}$ and $g$ are $l$-decreasing.

Now, suppose that $\mathcal{E}$ is $l$ increasing and $g$ is $l$-decreasing. Then ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})$, ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}g^{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}g_{\star}({\varrho})$. Also,

And,

By comparing (2.2) and (2.3), we conclude that ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}(\mathcal{E}({\varrho})+g({\varrho})) = {^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho})\ominus_{g}(-1){^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}g({\varrho})$.

Since $\mathcal{E}+g$ is $l$-increasing and decreasing, we get ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}(\mathcal{E}({\varrho})+g({\varrho}))\subseteq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}({\varrho})+{^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}g({\varrho})$, and the opposite case can be obtained by a similar procedure.

Hence, the required results are achieved. □

Theorem 2.6. Let $\mathcal{E}, g:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}$ be right ${\mathtt{q}}$-symmetric differentiable mappings and $l(\mathcal{E})-l(g)$ have constant sign over domain. Then, $\mathcal{E}\ominus_{g} g$ is a right ${\mathtt{q}}$-symmetric differentiable if one of the following cases hold

(1) If $\mathcal{E}, g$ are equally $l$-monotonic on $[{\sigma_{1}}, {\delta_{1}}]$, then

(2) If $\mathcal{E}, g$ are differently $l$-monotonic on $[{\sigma_{1}}, {\delta_{1}}]$, then

Proof. Assume that $l(\mathcal{E})\geq l(g)$ and $\mathcal{E}\ominus_{g} g = [\mathcal{E}_{\star}-g_{\star}, \, \mathcal{E}^{\star}-g^{\star}]$.

Suppose $\mathcal{E}, g$ are $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable and $l$-increasing on $[{\sigma_{1}}, {\delta_{1}}]$. Then, $\mathcal{E}_{\star}, \mathcal{E}^{\star}, g_{\star}$ and $g^{\star}$ are left ${\mathtt{q}}$-symmetric differentiable, and ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})$, ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}g_{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}g^{\star}({\varrho})$. Then, $\mathcal{E}_{\star}-g_{\star}$ and $\mathcal{E}^{\star}-g^{\star}$ are ${\mathtt{q}}$-symmetric differentiable, and thus $\mathcal{E}\ominus_{g}g$ is a right ${\mathtt{q}}$-symmetric differentiable function such that

By similar proceedings, we can obtain the result that both $\mathcal{E}$ and $g$ are $l$-decreasing.

Now, suppose that $\mathcal{E}$ is $l$ increasing and $g$ is $l$-decreasing. Then, ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}_{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}\mathcal{E}^{\star}({\varrho})$, ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}}g^{\star}({\varrho})\leq {^{{\delta_{1}}}D_{{\mathtt{q}}, s}}g_{\star}({\varrho})$. Also,

And,

Comparing (2.4) and (2.5) yields the required result. □

2.2.   $^{{\delta_{1}}}I_{{\mathtt{q}}, s}^{i}$-integral operator and its properties

In the current part of the study, we introduce the concept of $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric integral operator and its essential characterization. For our convenience, we specify the space of $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric integrable mappings and the space of all continuous $\mathcal{I}.\mathcal{V}$ mappings by $^{{\delta_{1}}}I_{{\mathtt{q}}, s}^{i}$ and ${\upsilon}([{\sigma_{1}}, {\delta_{1}}], \mathbb{R}_{I})$ respectively.

Definition 2.2. Let $\mathcal{E}\in {\upsilon}([{\sigma_{1}}, {\delta_{1}}], \mathbb{R}_{I})$. Then, the $^{{\delta_{1}}}I_{{\mathtt{q}}, s}^{i}$-integral operator is described as:

One can easily observe that a function is considered to be $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric integrable if $\sum_{n = 0}^{\infty}{\mathtt{q}}^{2n}\mathcal{E}({\mathtt{q}}^{2n+1}{\sigma_{1}}+(1-{\mathtt{q}}^{2n+1}){\delta_{1}})$ converges.

Theorem 2.7. Let $\mathcal{E}\in {\upsilon}([{\sigma_{1}}, {\delta_{1}}], \mathbb{R}_{I})$. Then, $\mathcal{E}\in ^{{\delta_{1}}}I_{{\mathtt{q}}, s}^{i}$ $\Leftrightarrow$ both $\mathcal{E}_{\star}$ and $\mathcal{E}^{\star}$ are right ${\mathtt{q}}$-symmetric integrable mappings. Also,

Proof. Consider $\mathcal{E}\in \, ^{{\delta_{1}}}I_{{\mathtt{q}}, s}^{i}$. Then,

This implies that both $\mathcal{E}_{\star}$ and $\mathcal{E}^{\star}$ are right ${\mathtt{q}}$-symmetric integrable mappings.

Conversely, suppose that $\mathcal{E}_{\star}$ and $\mathcal{E}^{\star}$ are ${\mathtt{q}}$-symmetric integrable mappings and $\mathcal{E}_{\star}\leq \mathcal{E}^{\star}$. Then, the result is obvious.

So, the result is proven. □

Example 2.2. Let $\mathcal{E}:[0, 2]\rightarrow \mathbb{R}_{I}$ such that $\mathcal{E}({\kappa}) = [2{\kappa}, 3{\kappa}^2]$. Then,

Theorem 2.8. Let $\mathcal{E}, g\in {\upsilon}([{\sigma_{1}}, {\delta_{1}}], \mathbb{R}_{I})$ and $({\sigma_{1}}, {\varrho})\subseteq [{\sigma_{1}}, \, {\delta_{1}}]$. Then, for $\alpha\in \mathbb{R}_{I}$ :

(1) $\int_{\sigma_{1}}^{\delta_{1}}[\mathcal{E}({\kappa})+g({\kappa})]{\, {^{{\delta_{1}}}\mathrm{d}_{{\mathtt{q}}}^{s}}}{\kappa} = \int_{\sigma_{1}}^{\delta_{1}}{\mathcal{E}}({\kappa}){\, {^{{\delta_{1}}}\mathrm{d}_{{\mathtt{q}}}^{s}}}{\kappa}+\int_{\sigma_{1}}^{\delta_{1}}g({\kappa}){\, {^{{\delta_{1}}}\mathrm{d}_{{\mathtt{q}}}^{s}}}{\kappa}.$

(2) $\int_{\sigma_{1}}^{\delta_{1}}(\alpha \mathcal{E})({\kappa}){\, {^{{\delta_{1}}}\mathrm{d}_{{\mathtt{q}}}^{s}}}{\kappa} = \alpha\int_{\sigma_{1}}^{\delta_{1}}{\mathcal{E}}({\kappa}){\, {^{{\delta_{1}}}\mathrm{d}_{{\mathtt{q}}}^{s}}}{\kappa}.$

Proof. From Definition 2.2,

Hence, the first proof is obtained. The proof of the second result is obvious. □

Theorem 2.9. Let $\mathcal{E}, g\in {\upsilon}([{\sigma_{1}}, {\delta_{1}}], \mathbb{R}_{I})$ and $({\sigma_{1}}, {\varrho})\subseteq [{\sigma_{1}}, \, {\delta_{1}}]$. Then,

Furthermore, $l(\mathcal{E})-l(g)$ has constant sign on $[{\sigma_{1}}, {\delta_{1}}]$, thus

Proof. We observe that

Also, we have

Comparison of (2.6) and (2.7) results in the desired inequality.

By the notion of generalized Hukuhara difference, if $l(\mathcal{E})\geq l(g)$, then $\mathcal{E}\ominus_{g}g = [\mathcal{E}_{\star}-g_{\star}, \, \mathcal{E}^{\star}-g^{\star}]$, and if $l(\mathcal{E})\leq l(g)$, then $[\mathcal{E}^{\star}-g^{\star}, \, \mathcal{E}_{\star}-g_{\star}]$. We suppose that $l(\mathcal{E})\geq l(g)$ on $[{\sigma_{1}}, {\delta_{1}}]$ such that $\mathcal{E}\ominus_{g}g = [\mathcal{E}_{\star}-g_{\star}, \, \mathcal{E}^{\star}-g^{\star}]$. This implies that $\int_{\sigma_{1}}^{\delta_{1}}(\mathcal{E}_{\star}-g_{\star}){\, {^{{\delta_{1}}}\mathrm{d}_{{\mathtt{q}}}^{s}}}{\kappa}\leq \int_{\sigma_{1}}^{\delta_{1}}(\mathcal{E}^{\star}-g^{\star}){\, {^{{\delta_{1}}}\mathrm{d}_{{\mathtt{q}}}^{s}}}{\kappa}$. Now,

Hence, the desired result is obtained. □

Theorem 2.10. Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ be right a ${\mathtt{q}}$-symmetric differentiable function on $({\sigma_{1}}, {\delta_{1}})$ and ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}(\mathcal{E}({\varrho})\in {\upsilon}([{\sigma_{1}}, {\delta_{1}}], \mathbb{R}_{I})$. If $\mathcal{E}$ is $l$-monotone on $[s, {\kappa}]$, then

Proof. If $\mathcal{E}$ is a $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function, then $\mathcal{E}_{\star}$ and $\mathcal{E}^{\star}$ are right ${\mathtt{q}}$-symmetric differentiable mappings, so $_{{\sigma_{1}}}D_{{\mathtt{q}}, s}\mathcal{E}_{\star}$ and $_{{\sigma_{1}}}D_{{\mathtt{q}}, s}\mathcal{E}^{\star}$ are right ${\mathtt{q}}$-symmetric integrable mappings. Therefore, $\mathcal{E}$ is also a $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric integrable function. If $\mathcal{E}$ is $l$-increasing on $[{\sigma_{1}}, {\delta_{1}}]$, then ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}(\mathcal{E}({\kappa}) = \left[{^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}_{\star}({\kappa}), \, {^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}^{\star}({\kappa})\right]$, and then

Since $\mathcal{E}_{\star}\leq \mathcal{E}^{\star}$ and from (2.9) and (2.10), we acquire

Now, from the notion of $gh$-difference, then

If $\mathcal{E}$ is $l$-decreasing on $[{\sigma_{1}}, {\delta_{1}}]$, then ${^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}(\mathcal{E}({\kappa})) = \left[{^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}^{\star}({\kappa}), \, {^{{\delta_{1}}}D_{{\mathtt{q}}, s}^{i}}\mathcal{E}_{\star}({\kappa})\right]$, and

Hence, the required result is acquired. □

Remark 2.2. If $\mathcal{E}$ is $l$-increasing, then (2.8) can be interpreted as

If $\mathcal{E}$ is $l$-decreasing, then (2.8) can be interpreted as

It is interesting to observe that the above result does not hold, if $\mathcal{E}$ is not $l$-monotone.

2.3.   Applications to Hermite-Hadamard's inequality

Now we develop the trapezium type inequalities by utilizing the $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric integral operator.

Theorem 2.11. Suppose $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ is an $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function. Then

Proof. Since $\mathcal{E}$ is an $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function on $({\sigma_{1}}, {\delta_{1}})$, there exist two tangents at $\frac{{\sigma_{1}}{\mathtt{q}}^2+{\delta_{1}}}{1+{\mathtt{q}}^2}$ given as

and

Since $\mathcal{E}$ is an $\mathcal{I}.\mathcal{V}$ convex function, $H_{1}({\varrho})\subseteq \mathcal{E}({\varrho})$, and then applying the $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric integration, we have

Now we establish the proof of second containments.

Moreover, the secant line through $({\sigma_{1}}, \mathcal{E}({\sigma_{1}}))$ and $({\delta_{1}}, \mathcal{E}({\delta_{1}}))$ can be expressed as:

and

Since $\mathcal{E}({\varrho}) = [\mathcal{E}_{\star}({\varrho}), \, \mathcal{E}^{\star}({\varrho})]$ is an $\mathcal{I}.\mathcal{V}$ convex mapping and ${\omega_{1}}({\varrho})\subseteq \mathcal{E}({\varrho})$, then

□

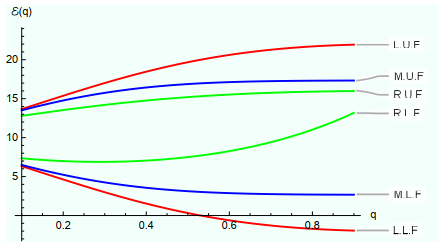
Example 2.3. Let $\mathcal{E}:[0, 2]\rightarrow \mathbb{R}_{I}$ be an $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function such that $\mathcal{E}({\varrho}) = [2{\varrho}^2, \, -2{\varrho}^2+20]$. Then, from Theorem 2.11, we obtain

Next, the $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric derivative of $\mathcal{E}$ is given as $^{{\delta_{1}}}D_{{\mathtt{q}}, s}\mathcal{E}({\varrho}) = \left[-4(2-{\mathtt{q}}), \, 4(2-{\mathtt{q}})\right]$.

Furthermore, the $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric integral of $\mathcal{E}$ is given as

From the above computations, we have the following containment:

For ${\mathtt{q}} = \frac{1}{3}$ in (2.14), we have

For graphical validation (Figure 1), we take ${\mathtt{q}}\in(0, 1)$ in (2.14).

Theorem 2.12. Suppose $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}$ is an $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function. Then,

Proof. Since $\mathcal{E}$ is an $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function on $({\sigma_{1}}, {\delta_{1}})$, there exist two tangents at $\frac{{\sigma_{1}}+{\delta_{1}}{\mathtt{q}}^2}{1+{\mathtt{q}}^2}$ given as

and

Since $\mathcal{E}$ is an $\mathcal{I}.\mathcal{V}$ convex function, $H_{2}({\varrho})\subseteq \mathcal{E}({\varrho})$, and then applying the $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric integration, we have

□

Example 2.4. Let $\mathcal{E}:[0, 2]\rightarrow \mathbb{R}_{I}$ be an $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function such that $\mathcal{E}({\varrho}) = [2{\varrho}^2, \, -2{\varrho}^2+20]$. Then, from Theorem 2.12, we obtain:

From (2.17) and (2.13), we obtain the following expression for Theorem 2.12:

For ${\mathtt{q}} = \frac{1}{3}$ in (2.18), we have

For graphical validation (Figure 2), we take ${\mathtt{q}}\in(0, 1)$ in (2.18).

Theorem 2.13. Let $\mathcal{E}:[{\sigma_{1}}, {\delta_{1}}]\rightarrow \mathbb{R}_{I}^{+}$ be an $\mathcal{I}.\mathcal{V}$ convex function. Then,

Proof. Since $\mathcal{E}$ is an $\mathcal{I}.\mathcal{V}$ convex function, then

Applying quantum symmetric integration on $(2.19)$ with respect to $'{{\varrho}}'$ over $[0, 1]$, we have

and

Similarly,

The combination of (2.20)–(2.22), results in the first containment. To prove our second containment, we employ the convexity of $\mathcal{E}$. Hence, the result is completed. □

Example 2.5. Let $\mathcal{E}:[0, 2]\rightarrow \mathbb{R}_{I}$ be an $\mathcal{I}.\mathcal{V}$ right ${\mathtt{q}}$-symmetric differentiable function such that $\mathcal{E}({\varrho}) = [2{\varrho}^2, \, -2{\varrho}^2+20]$. Then, from Theorem 2.13, we obtain:

For ${\mathtt{q}} = \frac{1}{3}$ in (2.23), we have

For graphical validation (Figure 3), we take ${\mathtt{q}}\in(0, 1)$ in (2.23).

3.   Conclusions

In the realm of mathematical analysis, one of the key research aims is how to find the derivative of absolute functions, which are not differentiable at certain points. To handle such kinds of problems, symmetric calculus plays a vital role. In this paper, we have developed the concept of right interval-valued quantum symmetric operators and examined numerous properties of operators in the setting of interval analysis. We have discussed the utility of these operators in inequalities. In favor of our findings, some visuals have been provided. It is important to observe that the derivative of $\mathcal{I}.\mathcal{V}$ functions involving absolute functions can be computed from our proposed operators. We hope these operators and techniques will create new avenues of research. Based on these operators, several kinds of inequalities can be obtained. Also, by utilizing these operators, several results of optimization theory can be updated. In the future, we will try to establish some error bounds of numerical formulas in the interval-domain associated with the developed theory.

Author contributions

Yuanheng Wang: conceptualization, investigation, writing-review and editing, visualization, validation; Muhammad Zakria Javed: conceptualization, software, formal analysis, investigation, writing-original draft preparation, writing-review and editing, visualization; Muhammad Uzair Awan: conceptualization, software, validation, formal analysis, investigation, writing-review and editing, visualization, supervision; Bandar Bin-Mohsin: conceptualization, validation, investigation, writing-review and editing, visualization; Badreddine Meftah: conceptualization, software, validation, formal analysis, investigation, writing-review and editing, visualization; Savin Treanta: conceptualization, software, investigation, writing-review and editing. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This research is supported by "The National Natural Science Funds of China (No. 12171435)". Prof Bandar is thankful to King Saud University, Riyadh, Saudi Arabia for the project "Researchers Supporting Project number (RSP2024R158), King Saud University, Riyadh, Saudi Arabia". The authors are thankful to the editor and the anonymous reviewers for their valuable comments and suggestions.

Conflict of interest

The authors declare no conflict of interest.