Rational solutions of an extended (2+1)-dimensional Camassa-Holm- Kadomtsev-Petviashvili equation in liquid drop

1.   Introduction

Let $\mathcal{D}\subset\Re^n$ be a nonempty, closed and convex set and $f : \Re^n\rightarrow \Re^n$ be a given continuous and monotone mapping. The variational inequality problem, denoted by Ⅵ($\mathcal{D}, f$), is to find a vector $x^*\in \mathcal{D}$ such that

The Ⅵ($\mathcal{D}, f$) has found many important applications in areas such as nonlinear complementarity problems (where $\mathcal{D} = \Re_{+}^{n}$) ^[1], traffic equilibrium and economic problems ^[2,3]. For recent applications and numerical methods of the Ⅵ($\mathcal{D}, f$), we refer the reader to ^[4,5,6] and the references therein.

In this paper, we consider a special case of the general Ⅵ problem, where the set $\mathcal{D}$ is assumed to have the following form:

here $A\in\Re^{m\times n}$ is a given matrix, $b\in\Re^{m}$ is a given vector, $\mathcal{X}\subset\Re^n$ is a nonempty, closed and convex subset. The solution set of (1.1) and (1.2), denoted by $\Omega^*$, is assumed to be nonempty. Note that the Ⅵ problem (1.1) and (1.2) is closely related to the convex optimization problem with linear equality constraints:

To show this, we recall the first order optimization conditions of problem (1.3). Let $x^*$ be a minimum point of the convex function $\theta(x)$ over $\mathcal{D}$ and $\xi^*$ be any vector in $\partial \theta(x^*)$, where $\partial \theta(\cdot)$ denotes the subdifferential operator of $\theta(\cdot)$. Then for any feasible direction $d\in\Re^n$ at $x^*$, we have $(\xi^*)^Td > 0$. It means that, the following variational inequality problem is captured:

Thus, solving the Ⅵ problem (1.4) amounts to solving (1.3). This Ⅵ characterization is also used in e.g., ^[7,8].

The Ⅵ problem (1.1) and (1.2) or its equivalent form (1.3) is one of the fundamental problems in convex optimization. In particular, it includes linear programming, conic and semidefinite optimization as special cases. It can find many applications in compressed sensing, image processing and data mining, see, e.g., ^[9,10,11]. We refer to ^[12] for recent examples and discussions. To solve the Ⅵ problem (1.1) and (1.2), some proximal-like algorithms have been developed over the past years, see e.g., ^[13] for a review. One benchmark method is the augmented Lagrangian Method (ALM) ^[14,15] for nonlinear problems. The ALM is applicable to solve Ⅵ($\mathcal{D}, f$) (1.1) and (1.2). More specifically, for a given $u^{k} = (x^{k}, \lambda^{k})$, ALM uses the following procedure to carry out the new iteration $u^{k+1} = (x^{k+1}, \lambda^{k+1})\in\mathcal{X}\times\Re^m$:

Find ${x}^{k+1}\in\mathcal{X}$ such that

then update $\lambda^{k+1}$ via

where $\beta\geq 0$ is a given penalty parameter for the violation of the linearly constraints. To make ALM (1.5) more efficient and flexible, some alternative strategies can be used. For example, some self-adaptive rules can be carried to adjust the parameter $\beta$ based on certain strategies ^{[16,17,18,19]}. We can also use some correction technologies to the output point ^[20,21]. Let $\tilde{ u}^k$ denote the predictor generated by ALM. A simple and effective correction scheme is

where $0 < \alpha_{k} < 2$ is the step size parameter; see, e.g., ^[22,23] for details.

The main computational cost at each iteration of ALM is to solve the subproblem (1.5a), which is still a variational inequality, structurally the same as the original problem. So in many cases the ALM (1.5a) is easy to iterate only if $A$ is an identity matrix. This is because, for this case, the solution of the subproblem (1.5a) corresponds to the proximal mappings of $f$ and it usually has closed-form solutions or can be efficiently solved up to a high precision. However, in many applications in sparse optimization, we often encounter the case where $A$ is not an identity matrix, and the resulting subproblem (1.5a) no longer has closed-form solutions. For this case, solving the subproblem (1.5a) could be computationally intensive because of the costly evaluation of $(A^TA+\frac{1}{\beta}f)^{-1}(A\upsilon)$. Therefore, efficient numerical methods with implementable iterative scheme are highly desired.

Recently, several techniques attempting to overcome this difficulty have been proposed. In the framework of the proximal point algorithm (PPA), there are two relevant approaches. The first one is regularization. By adding a customized regularization term to the saddle-point reformulation of (1.1) and (1.2), the primal subproblem becomes easy as it only involves a simple evaluation, see the customized PPA algorithms proposed in e.g., ^{[24,25,26,27]}. We refer the reader to e.g., ^[28,29] of the linearized regularization term for the separable case of problem (1.2). The second one employs prediction-correction technology which adds an asymmetrical proximal term to make a prediction, and then introduces a simple correction step to guarantee the convergence, see e.g., ^[30,31,32]. In this paper, we propose a new prediction-correction method for the Ⅵ($\mathcal{D}, f$). At each iteration, the method first makes a simple prediction step to obtain a point, and then generates a new iteration via a minor correction to the predictor. The reduced subproblems are easy to solve when the resolvent mapping of $f$ can be efficiently evaluated. As can be seen in the Section 5, the proposed method converges faster with less iterations to achieve the same accuracy on most numerical cases.

The rest of this paper is organized as follows. In Section 2, we review some preliminaries which are useful for further analysis. In Section 1, we present the implementable prediction-correction method for Ⅵ($\mathcal{D}, f$). In Section 4, we establish the global convergence of the proposed method. The computational experiment is presented in Section 5. Finally, we make a conclusion in Section 6.

2.   Preliminaries

2.1.   Equivalent VI

In this section, we reformulate the Ⅵ problem (1.1) and (1.2) in succinct form. Let $\Omega = \mathcal{X}\times\Re^m$. By attaching a Lagrange multiplier vector $\lambda\in\Re^m$ to the linear constraints $Ax = b$, the Ⅵ problem (1.1) and (1.2) can be converted to the following form:

By denoting

we can rewrite (2.1) into the following more compact form

Henceforth, we will denote the Ⅵ problem (2.2) and (2.3) by Ⅵ($\Omega, F$). Now, we make some basic assumptions and summarize some well known results of Ⅵ, which will be used in subsequent analysis.

2.2.   Assumption

${\bf{ (A1)}}$ $\mathcal{X}$ is a simple closed convex set.

A set is said to be simple if the projection onto it can be easily obtained. Here, the projection of a point $a$ onto the closed convex set $\mathcal{X}$, denoted by $P_{\mathcal{X}}(a)$, is defined as the nearest point $x\in\mathcal{X}$ to $a$, i.e.,

${\bf{(A2)}}$ The mapping $f$ is point-to-point, monotone and continuous.

A mapping $F:\Re^n\rightarrow \Re^n$ is said to be monotone on $\Omega$ if

${\bf{(A3)}}$ The solution set of (2.2) and (2.3), denoted by $\Omega^*$, is nonempty.

Remark 1. The mapping $F(\cdot)$ defined in (2.3) is monotone with respect to $\Omega$ since

Proof.

where the last inequality follows from the monotone property of $f$. □

2.3.   Properties

Let $G$ be a symmetric positive definite matrix. The $G$-norm of the vector $u$ is denoted by $\| u\|_G: = \sqrt{\langle u, G u\rangle}$. In particular, when $G = I$, $\| u\| : = \sqrt{\langle u, u\rangle}$ is the Euclidean norm of $u$. For a matrix $A$, $\|A\|$ denotes its norm $\|A\|: = \text{max}\{\|Ax\|: \|x\|\leq 1\}$.

The following well-known properties of the projection operator will be used in the coming analysis. The proofs can be found in textbooks, e.g., ^[2,33].

Lemma 1. Let $\mathcal{X}\in\Re^n$ be a nonempty closed convex set, $P_{\mathcal{X}}(\cdot)$ be the projection operator onto $\mathcal{X}$ under the $G$-norm. Then

For any arbitrary positive scalar $\beta$ and $u\in\Omega$, let $e(u, \beta)$ denote the residual function associated with the mapping $F$, i.e.,

Lemma 2. Solving VI($\Omega, F$) is equivalent to finding the zero point of the mapping

Proof. See ^[2], pp 267. □

3.   The prediction-correction method

We now formally present the new prediction-correction method for the Ⅵ($\Omega, F$) (Algorithm 1). The method can be viewed as a generalization of ^[31] in relaxed case.

Remark 2. Note that the regularized projection Eq (3.2a) amounts to solving the following VI problem

which represents to find $\tilde{x}^k\in\mathcal{X}$ such that

We can rewrite the above equation as

Thus, the subproblem (3.2a) is equivalent to an evaluation of the resolvent operator $(I+\frac{1}{r}f)^{-1}$ when $\mathcal{X}$ is the finite-dimensional Euclidean spaces ^[34]. Notice that ALM (1.5a) needs to evaluate the operator $(A^TA+\frac{1}{\beta}f)^{-1}$. Therefore, the resulting subproblem (3.2a) could be much easier to solve than ALM (1.5a). On the other hand, the correction step only consists of some elementary manipulations. Thus, the resulting method (3.2a)–(3.3b) is easily implementable.

Remark 3. The parameters $\frac{1}{r}$ and $\frac{1}{s}$ in the prediction step can be viewed as two step sizes for the projection step (3.2a) and dual step, respectively. Using the step size condition $rs > \frac{1}{4}\|A^TA\|$ of this algorithm, the parameters $\frac{1}{r}$ and $\frac{1}{s}$ can be chosen larger values compared to the condition $rs > \|A^TA\|$ of some other primal dual algorithms, e.g., linearized ALM, customized PPA algorithms. This larger step size is usually beneficial to the effectiveness and robustness of the algorithm. In Section 5 we will empirically see that our algorithm is significantly faster than some other primal dual algorithms by allowing larger step sizes.

4.   Convergence properties

In the following, we will focus our attention to solving Ⅵ($\Omega, F$). But at the beginning, to make the notation of the proof more succinct, we define some matrices:

Obviously, when $rs > \frac{1}{4}\|A^TA\|$, $G$ is a positive definite matrix. Now, we start to prove the global convergence of the sequence $\{ u^k\}$. Towards this end, we here follow the work ^[35] to reformulate the algorithm into a prediction-correction method and establish its convergence results. We first prove some lemmas. The first lemma quantifies the discrepancy between the point $\tilde{ u}^k$ and a solution point of Ⅵ($\Omega, F$).

Lemma 3. Let $\{u^k\}$ be generated by the PCM and $\{\tilde{u}^k\}$ be generated by PCM (3.2), and the matrix $Q$ be given in (4.1). Then we have

Proof. Note that the sequence $\{\tilde{ u}^k\}$ generated by (3.2) is actually solutions of the following VIs:

and

Combining (4.3) and (4.4) yields

It can be rewritten as

Using the notation of $F(u)$ (2.3) and $Q$ (4.1), the assertion (4.2) is proved. □

The following lemma characterizes the correction step by a matrix form.

Lemma 4. Let $\{u^k\}$ be generated by the PCM and $\{\tilde{u}^k\}$ be generated by PCM (3.2), Then we have

where

Proof. From the correction Step (3.3a) and (3.3b), we have

which can be written as

By noting the matrix $M$ (4.8), the proof is completed. □

Using the matrices $Q$ (4.1) and $M$ (4.8), we define

then we have $Q = HM$. The inequality (4.2) can be written as

Substituting (4.7) into (4.12) and using the monotonicity of $F$ (see (2.5)), we obtain

Now, we prove a simple fact for the matrix $H$ in the following lemma.

Lemma 5. The matrix $H$ defined in (4.11) is positive definite for any $r > 0, s > 0$, $rs > \frac{1}{4}\|A^TA\|$.

Proof. For the matrix $Q$ defined by (4.1), we have

Thus, it follows from (4.1) that

For any any $r > 0, s > 0$ satisfying $rs > \frac{1}{4}\|A^TA\|$, $H^{-1}$ is positive definite, and the positive definiteness of $H$ is followed directly. □

Then we show how to deal with the right-hand side of (4.13). The following lemma gives an equivalent expression of it in terms of $\|u-u^k\|_H$ and $\|u-u^{k+1}\|_H$.

Lemma 6. Let $\{u^k\}$ be generated by the PCM and $\{\tilde{u}^k\}$ be generated by PCM (3.2). Then we have

where the matrix $G = \gamma(Q^T+Q)-\gamma^2M^THM$.

Proof. Applying the identity

to the right term of (4.13) with $a = u, b = \tilde{u}^k, c = u^k, d = u^{k+1}$, we obtain

For the last term of (4.17), we have

the assertion is proved. □

Now, we investigate the positive definiteness for the matrix G. Using (4.11), we have

Thus, when $rs > \frac{1}{4}\|A^TA\|$ and $\gamma\in(0, 2)$, the matrix $G$ is guaranteed to be positive definite, and we can easily obtained the contraction property of the algorithm. This is given by the following theorem.

Theorem 1. Suppose the condition

holds. Let the relaxation factor $\gamma\in(0, 2)$. Then, for any $u^{*} = (x^{*}, \lambda^{*})^T\in\Omega^*$, the sequence $u^{k+1} = (x^{k+1}, \lambda^{k+1})^T$ generated by PCM satisfies the following inequality:

Proof.

Combining (4.13) and (4.15), we have

Note that $u^*\in\Omega$. We get

Since $u^*$ is a solution of (2.3) and $\tilde{ u}^k\in\Omega$, we have

and thus

The assertion (4.21) follows directly. □

Based on the above results, we are now ready to prove the global convergence of the algorithm.

Theorem 2. Let $\{u^k\}$ be the sequence generated by PCM for the Ⅵ problem (2.2) and (2.3). Then, for any $r > 0, s > 0$ satisfying $rs > \frac{1}{4}\|A^TA\|$ and $\gamma\in(0, 2)$, the sequence $\{ u^{k}\}$ converges to a solution of Ⅵ($\Omega, F$).

Proof. We follows the standard analytic framework of contraction-type methods to prove the convergence of the proposed algorithm. It follows from Theorem 1 that $\{ u^{k}\}$ is bounded. Then we have that

Consequently,

and

Since

and

it follows from (4.25) and (4.26) that

Because $\tilde{u}^k$ is also bounded, it has at least one cluster point. Let $u^\infty$ be a cluster point of $\tilde{u}^k$ and let $\tilde{u}^k_j$ be the subsequence converges to $u^\infty$. It follows from (4.29) that

Consequently, we have

Using the continuity of $F$ and the projection operator $P_{\Omega}(\cdot)$, we have that $u^\infty$ is a solution of Ⅵ($\Omega, F$). On the other hand, by taking limits over the subsequences in (4.24) and using $\lim_{j\rightarrow \infty} \tilde{u}^k_j = u^\infty$. we have that, for any $k > k_j$,

Thus, the sequence $\{ u^{k}\}$ converges to $u^\infty$, which is a solution of Ⅵ($\Omega, F$). □

5.   Numerical experiments

In this paper, we test the performance of PCM (3.2a)–(3.3b) for solving the basis pursuit (BP) and matrix completion problem. All the simulations are performed on a Lenovo Laptop with CPU Intel with 2.81GHz and 16GB RAM memory, using Matlab R2015b.

5.1.   Basis pursuit problem

The BP problem arises from areas such as the communities of information theory, signal processing, statistics, machine learning. it seeks to encode a large sparse signal representations through a relatively small number of linear equations. The BP problem can be cast as the following equality-constrained $l_1$ minimization problem

where $x\in\Re^n$, data $A\in\Re^{m\times n}$ with $m < n$, $b\in\Re^m$. Here we assume that $A$ has full row rank. By invoking the first-order optimality condition, BP is equivalent to Ⅵ (1.1) and (1.2) with $f(x) = \partial\|x\|_1$. Applying PCM with $\gamma = 1$ for this problem, we get the following iterative scheme:

Note that the projection (5.2a) is equivalent to the $l_1$ shrinkage operation:

where the $l_1$ shrinkage operator, denoted by $\mbox{Shrink}(M, \xi)$, is defined as

In our experiments, we focus on comparing our algorithm with the linearized ALM ^[36] (L-ALM) and the customized PPA (C-PPA) in ^[27] and verifying its efficiency. Similar with PCM, L-ALM and C-PPA also depend on Shrink operation, which have the same easiness of implementation.

The data used in this experiment is similar to the one employed in ^[37]. The basic setup of the problem is as follows. The data matrix $A$ is a i.i.d. standard Gaussian matrix generated by the randn(m, n) function in MATLAB with $m = n/2$. The original sparse signal $x_{\mbox{true}}$ is sampled from i.i.d. standard Gaussian distributions with $m/5$ nonzero values. The output $b$ is then created as the signs of $b = Ax$. It is desirable to test problems that have a precisely known solution. In fact, when the original signal $x_{\mbox{true}}$ is very sparse, it reduces to a minimization problem. The parameters used in the numerical experiments are similar to that in ^[19,38]: we set the relaxation factor $\gamma = 1$, $s\in (25,100)$, $r = 1.01\|A^TA\|/(4s)$ for PCA and $s\in(25,100)$, $r = 1.01\|A^TA\|/s$ for C-PPA. (In order to ensure the convergence of L-ALM and C-PPA, the parameters $r, s$ should satisfy $rs > \|A^TA\|$.) We set the criterion error as $\!\min\{ \text{rel}_L = \|x^k-x^{k-1}\|, \text{rel}_S = Ax^k - b\}$, and declare successful recovery when this error is less than $Tol = 10^{-3}$. In all the tests, the initial iteration is $(x^0, \lambda^0) = (\textbf{0}, \textbf{1})$.

We first test the sensitivity of $\gamma$ of PCM. We fix $s = 50$ and choose different values of $\gamma$ in the interval $[0.6, 1.8]$. The number of iterations required are reported in Figure 1. The curves in Figure 1 indicate that $\gamma\in (1, 1.4)$ is preferable when we implement Algorithm PCM in practice.

In order to investigate the stability and efficiency of our algorithms, we test $8$ groups of problems with different $n$ and we generated the model by 10 times and reported the average results. The comparisons of these algorithms for small BP problems are presented in Tables 1–3.

From Tables 1–3, it can be seen that the PCM performs the best, both in terms of number of iterations and CPU time for all test cases. These numerical results illustrate that if the step size condition relaxed, can indeed be beneficial to yield larger step sizes, which could accelerate the convergence of algorithm.

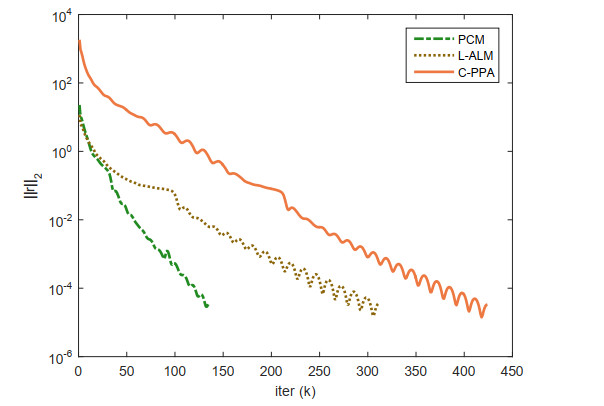
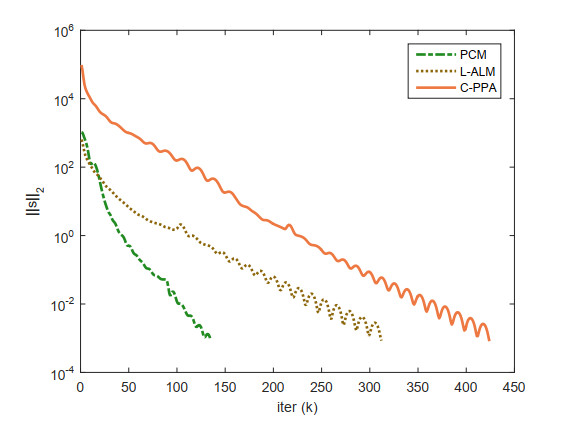
To verify the performance results of our algorithm, we plotted the approximation error $\text{rel}_L = \|x^k-x^{k-1}\|, \text{rel}_S = \|Ax^k - b\|$ achieved for $n = 1500, s = 50$ by each of the algorithms versus the iteration number $k$ in Figures 2 and 3, respectively. It is clear to see that PCM outperforms all the other algorithms significantly in terms of number of iterations.

5.2.   Matrix completion problem

Matrix completion problem (MC) comes from many fields such as signal processing, statistics, machine learning communities. It tries to recover the low-rank matrix $X$ from its incomplete known entries. Mathematically, its convex formula is as follows:

where $\|X\|_*$ is the nuclear norm of X, $M$ is the unknown matrix with $p$ available sampled entries and $\Omega$ is a set of pairs of indices of cardinality $p$. By invoking the first-order optimality condition, MC can also be equivalent to Ⅵ (1.1) and (1.2) with $f(x) = \partial\|X\|_*$.

The basic setup of the problem is as follows. We first generate two random matrices $M_L \in \Re^{n\times r_a}$ and $M_R \in \Re^{n\times r_a}$, all with i.i.d. standard Gaussian entries, and then set the low-rank matrix $M = M_LM_R^T$. The available index set $\Omega$ is randomly uniformly sampled in all cardinality sets $|\Omega|$. We denote the oversampling factor (OS) by $OS = |\Omega|/r_a(2n-r_a)$, i.e., the ratio of sample size to degrees of freedom in an asymmetric matrix of rank $r_a$. The relative error of the approximation $X$ is defined as

We set the relative error $Tol = 10^{-5}$ as the tolerance for all algorithms. In all tests, the initial iteration is $(X^0, \Lambda^0) = (\textbf{0}, \textbf{0})$. The parameters used in the numerical experiments are set as follows: we set $r = 0.006$, $s = 1.01/(4r)$, $\gamma = 1$ for PCM, $s = 1.01/r$ for L-ALM and C-PPA.

Tables 4–6 list the comparison between these algorithms with three different OS values. The results confirm that PCM outperforms other methods in terms of computation time and number of iterations in all cases.

6.   Conclusions

This paper proposes a new prediction-correction method for solving the monotone variational inequalities with linear constraints. At the prediction step, the implementation is carried out by a simple projection. At the correction step, the method introduces a simple updating step to generate the new iteration. We establish the global convergence of the method. The convergence condition of the method also allows larger step sizes that can in potential make the algorithm numerically converge faster. The numerical experiments approve the efficiency of the proposed methods. The future work is to explore combining self adaptive technique for the method. Besides, further applications of our method are expected.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by NSF of Shaanxi Province grant number 2020-JQ-485.

Conflict of interest

The authors declare no conflict of interest.