Input-to-state stability for discrete-time switched systems by using Lyapunov functions with relaxed constraints

Huijuan Li; Huijuan Li

doi:10.3934/math.20231576

AIMS Mathematics

2023, Volume 8, Issue 12: 30827-30845. doi: 10.3934/math.20231576

Previous Article Next Article

Research article

Input-to-state stability for discrete-time switched systems by using Lyapunov functions with relaxed constraints

Huijuan Li ^,

School of Mathematics and Physics, China University of Geosciences (Wuhan), Wuhan, 430074, China

Received: 10 September 2023 Revised: 23 October 2023 Accepted: 06 November 2023 Published: 15 November 2023
MSC : 34D05, 37B25, 93C10, 93C55, 93D20

In this paper, input-to-state stability (ISS) is investigated for discrete-time time-varying switched systems. For a switched system with a given switching signal, the less conservative assumptions for ISS are obtained by using the defined weak multiple ISS Lyapunov functions (WMISSLFs). The considered switched system may contain some or all subsystems which do not possess ISS. Besides, for an ISS subsystem the introduced Lyapunov function could be increasing along the trajectory of the subsystem without input at some moments. Then for a switched system under any switching signal, the relaxed sufficient constraints for ISS are attained by using the defined weak common ISS Lyapunov functions. For this case, each subsystem of the considered system must be ISS. The proposed function may be increasing along the trajectory of each ISS subsystem of the considered system without input at some instants. The relationship between WMISSLFs for a switched system and the defined weak multiple Lyapunov functions for this switched system without input is set up. Three numerical examples are investigated to display the usefulness of the principal outcomes. According to the main conclusions, an intermittent controller is applied to ensure ISS for a discrete-time disturbed Chua's chaotic system.

Keywords:

Citation: Huijuan Li. Input-to-state stability for discrete-time switched systems by using Lyapunov functions with relaxed constraints[J]. AIMS Mathematics, 2023, 8(12): 30827-30845. doi: 10.3934/math.20231576

Related Papers:

[1]	Yunpeng Xiao, Wen Teng . Representations and cohomologies of modified $\lambda$ -differential Hom-Lie algebras. AIMS Mathematics, 2024, 9(2): 4309-4325. doi: 10.3934/math.2024213
[2]	Senrong Xu, Wei Wang, Jia Zhao . Twisted Rota-Baxter operators on Hom-Lie algebras. AIMS Mathematics, 2024, 9(2): 2619-2640. doi: 10.3934/math.2024129
[3]	Lili Ma, Qiang Li . Cohomology and its applications on multiplicative Hom- $\delta$ -Jordan Lie color triple systems. AIMS Mathematics, 2024, 9(9): 25936-25955. doi: 10.3934/math.20241267
[4]	Xianguo Hu . Universal enveloping Hom-algebras of regular Hom-Poisson algebras. AIMS Mathematics, 2022, 7(4): 5712-5727. doi: 10.3934/math.2022316
[5]	Cenap Özel, Habib Basbaydar, Yasar Sñzen, Erol Yilmaz, Jung Rye Lee, Choonkil Park . On Reidemeister torsion of flag manifolds of compact semisimple Lie groups. AIMS Mathematics, 2020, 5(6): 7562-7581. doi: 10.3934/math.2020484
[6]	Wen Teng, Fengshan Long, Yu Zhang . Cohomologies of modified $\lambda$ -differential Lie triple systems and applications. AIMS Mathematics, 2023, 8(10): 25079-25096. doi: 10.3934/math.20231280
[7]	Muhammad Asad Iqbal, Abid Ali, Ibtesam Alshammari, Cenap Ozel . Construction of new Lie group and its geometric properties. AIMS Mathematics, 2024, 9(3): 6088-6108. doi: 10.3934/math.2024298
[8]	Junyuan Huang, Xueqing Chen, Zhiqi Chen, Ming Ding . On a conjecture on transposed Poisson $n$ -Lie algebras. AIMS Mathematics, 2024, 9(3): 6709-6733. doi: 10.3934/math.2024327
[9]	Nouf Almutiben, Ryad Ghanam, G. Thompson, Edward L. Boone . Symmetry analysis of the canonical connection on Lie groups: six-dimensional case with abelian nilradical and one-dimensional center. AIMS Mathematics, 2024, 9(6): 14504-14524. doi: 10.3934/math.2024705
[10]	Baiying He, Siyu Gao . The nonisospectral integrable hierarchies of three generalized Lie algebras. AIMS Mathematics, 2024, 9(10): 27361-27387. doi: 10.3934/math.20241329

Abstract

Nomenclature

$\vec{q}$	the fluid velocity vector
$p$	the fluid pressure at any point
$\rm{m}$	the couple stress tensor
$\rm{I}$	the unit dyadic
$\vec{w}$	the fluid vorticity vector
$E^{2}$	the axisymmetric Stokesian operator
$I_{n}(\cdot)$	the first kind for modified Bessel function of order $n$
$K_{n}(\cdot)$	the second kind for modified Bessel function of order $n$
$a$	radius of the spherical droplet
$b$	radius of the spherical interface
$s_{1}, s_{3}$	the spin parameters in Section $3$
$s_{2}$	the spin parameters in Section $4$
$t_{r\theta}^{(1)}, t_{r\theta}^{(2)}, t_{r\theta}^{(3)}$	the shear stresses for fluid flows in Section $3$
$\hat{t}_{r\theta}^{(1)}, \hat{t}_{r\theta}^{(2)}, \hat{t}_{r\theta}^{(3)}$	the shear stresses for fluid flows in Section $4$
$q_{r}^{(1)}, q_{r}^{(2)}, q_{r}^{(3)}$ and $q_{\theta}^{(1)}, q_{\theta}^{(2)}, q_{\theta}^{(3)}$	the velocity components for fluid flows in Section $3$
$\hat{q}_{r}^{(1)}, \hat{q}_{r}^{(2)}, \hat{q}_{r}^{(3)}$ and $\hat{q}_{\theta}^{(1)}, \hat{q}_{\theta}^{(2)}, \hat{q}_{\theta}^{(3)}$	the velocity components for fluid flows in Section $4$
$A_{1}, B_{1}, A_{2}, B_{2}, C_{2}, D_{2}, E_{2}, F_{2}, A_{3}, B_{3}$	unknowns in the system of the Eqs (54)--(63)
$\hat{A}_{1}, \hat{B}_{1}, \hat{A}_{2}, \hat{B}_{2}, \hat{C}_{2}, \hat{D}_{2}, \hat{A}_{3}, \hat{B}_{3}$	unknowns in the system of the Eqs (94)--(102)
$K$	the micropolar-viscous interface correction factor
$\hat{K}$	the viscous-micropolar interface correction factor
*Greek Letters*
$\Pi$	the stress tensor
$\vec{\nu}$	the fluid microrotation vector
$\vec{\epsilon}$	the unit triadic
$(k, \alpha, \beta, \gamma)$	the micropolar viscosity parameters
$(r, \theta, \phi)$	the spherical coordinate systems
$(\vec{e}_{r}, \vec{e}_{\theta}, \vec{e}_{\phi})$	the unit vectors
$\psi^{(1)}, \psi^{(2)}, \psi^{(3)}$	the stream functions for the fluid flows in Section $3$
$\hat{\psi}^{(1)}, \hat{\psi}^{(2)}, \hat{\psi}^{(3)}$	the stream functions for the fluid flows in Section $4$
$\omega_{\phi}^{(1)}, \omega_{\phi}^{(3)}$	the fluid vorticity components in Section $3$
$\omega_{\phi}^{(2)}$	the fluid vorticity component in Section $4$
$\nu_{\phi}^{(2)}$	the fluid microrotation component in Section $3$
$\nu_{\phi}^{(3)}$	the fluid microrotation component in Section $4$
$\mu_{1}, \mu_{2}, \mu_{3}$	the fluid's viscosity coefficients in Section $3$
$\hat{\mu}_{1}, \hat{\mu}_{2}, \hat{\mu}_{3}$	the fluid's viscosity coefficients in Section $4$

1. Introduction

For the past few years, there have been some noteworthy advancements in the field of fluid mechanics that are focused on structures inside fluids. The classical theory has been demonstrated to be insufficient for describing their behaviour. The earliest theory to take structured fluids into account is the theory of micropolar fluids, given by Eringen ^[1]. The mathematical representation of micropolar fluid allows us to discuss several physical phenomena resulting from the micro-motions and local structure of the particles. It provides a more accurate description of the behaviour of various real fluids, such as animal blood, liquid crystals, polymeric suspensions, and muddy fluids, than the classical representation of Navier-Stokes, particularly whenever the typical flow dimensions, such as the pipe diameter, shrink to a small size. It aligns closely with our assumptions that the greater the effect of the fluid's internal structure, the smaller the typical dimensions of the flow. There have been numerous studies on micropolar fluid flow in applications related to engineering ^[2,3,4] and industry ^[5,6,7].

At low Reynolds numbers, in cell/cavity models, the movement of a viscous/micropolar incompressible fluid on rigid particles or fluid droplets of different shapes is a topic of interest for researchers in biomedical, chemical, and environmental engineering and science. In many real-life situations, the area where fluids flow over groups of particles is important. This is true for sedimentation, fluidisation, the rheology of suspensions, the movement of blood cells found in veins or arteries, centrifugation, and micro-fluidics. As a result, it is crucial to ascertain whether the existence of nearby boundaries or particles affects the movement of a specific droplet or particle. The unit cavity/cell model is a notable and effective method that has been used to predict how the concentration of particles will affect the rate at which particles sediment ^[8].

The representation of the cell/cavity model includes the idea that a randomly assembled collection of droplets/particles may be separated into an identical number of cells/cavities, each containing a single droplet/particle that is typically spherical or elliptical. The fluid cell's volume is selected to ensure that the assemblage's solid volume fraction aligns with the cell's solid volume fraction. Therefore, each particle (droplet) causes the entire disruption by being restricted inside the fluid's cell it is linked to. The boundary value problem is simplified by considering only one droplet/particle and its surrounding envelope. The representation of the unit cell is commonly employed to analyse and address the boundary value problem in solid/fluid particles that are moving within concentrated cells/cavities, disregarding the influence of the container cell (cavity), such as ^[9,10,11].

The Stokes flow issue, which involves an incompressible fluid with a different viscosity surrounding a fluid sphere, has received a lot of attention in analytical and numerical discussions. This model is widely used in modern engineering applications. Hadamard ^[12] and Rybczynski ^[13] independently expanded the Stokes issue to study the translational movement of a fluid sphere droplet in another non-miscible fluid. They calculated the drag force that the surrounding fluid would exert on the fluid sphere by assuming that the shearing tension and tangential velocity at the interface between the two fluid phases are continuous. In real Stokes flow scenarios, droplets or particles are typically not in isolation and are surrounded by a fluid that is confined by solid cavities (walls). It is crucial to examine if the existence of nearby boundaries has a substantial impact on the movement of the droplet/particle. Using bipolar spherical coordinate systems, Bart ^[14] studied the movement of a spherical fluid droplet as it settled perpendicular to a planar interface, seperating between two immiscible newtonian fluid phases. Meanwhile, Salem et al. ^[15] studied the thermocapillary Stokes movement of a fluid sphere droplet in the presence of a planar interface. Hetsroni and Haber ^[16] investigated the issus of a solitary fluid sphere droplet immerged in an unlimited Newtonian fluid of varying viscosity. Also, some have studied examined the wall impacts on a spherical fluid droplet flowing along the centreline of a circular tube utilising a reciprocal theorem ^[17] and an approximate technique ^[18]; on the other hand, some studies the interface impacts on a spherical fluid droplet utilising the volume of fluid method ^[19,20,21]. Moreover, Lee et al. ^[22] showed the motion of a fluid droplet inside a non-concentric spherical cavity.

Every result mentioned above concerns viscous fluids. According to micropolar fluids, Ramkissoon ^[23,24] has discussed the Stokesian flow of a non-Newtonian fluid past a Newtonian fluid sphere and spheroid. Niefer and Kaloni ^[25] studied two interconnected issues involving the movement of a Newtonian fluid past a spherical fluid containing a non-Newtonian fluid, and, additionally, the movement of a non-Newtonian fluid past a Newtonian fluid droplet with a boundary condition for non-zero slip/spin. Hayakawa ^[26] examined the issues associated with the slow, axisymmetric Newtonian flow of a non-Newtonian fluid past a stationary sphere and cylinder; they explicitly analysed and determined the normalised drag force for each scenario, other studies, see ^[27,28].

The movement depends strongly on the interfacial area, which is a function of the size and shape of the particle, as well as the overall fluid motion. At the interface between a particle and the ambient fluid, for particle stability, a balance between the normal force, the shear force, and the surface tension force must be maintained. This balance governs the shape of the particle. The size would also be influenced, particularly if there is phase change. Accordingly, the encircling medium and the fluid particle is separated by a well-defined interface. In certain instances, such as a soap bubble, the separating interface can be a thin liquid film. There are many complex instances, consisting of pairs of bubbles and drops in contact, or a fluid particle entirely inside a drop. These systems are referred to as compound drops. The fluid medium surrounding drops and bubbles is one of the following phases ^[29]: $(i)$ drop inside liquid; $(ii)$ gas bubble inside liquid; $(iii)$ soap bubble (gas inside gas); $(iv)$ compound drop-two interfaces (liquid or gas inside liquid inside liquid or gas); and $(v)$ compound drop-three interfaces (at least two of the phases are liquid).

The aim of this study is to investigate the issue of a compound drop's mobility when two interfaces separating three immiscible liquid regions are present; the micropolar fluid is also one of the three fluid phases. The movement of a spherical viscous droplet in a micropolar fluid with an interface has not been investigated before. Thus, in this paper, we generalise the problem of Salem ^[30] to consider the translational movement of a spherical viscous droplet inside a spherical micropolar/viscous interface with concentric positions. The viscous sphere droplet is either immersed in viscous fluid or in micropolar fluid.

2. Mathematical equations

The equations describing the incompressible micropolar fluid in steady motion with negligible external forces and couplings, based on Stokes' assumption, are provided by ^[1]:

$\begin{eqnarray} &&div\, \vec{q} = 0, \end{eqnarray}$

(1)

$\begin{eqnarray} &&grad\, p-k\, curl\, \vec{\nu}+(\mu+k)\, curl\, curl\, \vec{q} = 0, \end{eqnarray}$

(2)

$\begin{eqnarray} &&k\, curl\vec{q}-2k\vec{\nu}+(\alpha+\beta+\gamma)\, grad\, div\, \vec{\nu}-\gamma\, curl\, curl\, \vec{\nu} = 0, \end{eqnarray}$

(3)

where $\vec{q}$ refers to the velocity vector; $\vec{\nu}$ refers to the microrotation vector; $p$ refers to the fluid pressure at any point; $\mu$ refers to the dynamic viscosity coefficient; and $(k, \alpha, \beta, \gamma)$ are the micropolar viscosity parameters. These coefficients follow standard inequality rules:

$\begin{equation*} \, 2\mu+k\geq\, 0;\, \, \, \gamma\geq\, 0;\, \, \, k\geq\, 0;\, \, \, 3\alpha+\beta+\gamma\geq\, 0;\, \, \, \gamma\geq|\beta|. \end{equation*}$

The constitutive equations, respectively, for the stress tensor, $\vec{ \rm{I}}$ , and the couple stress tensor, $\vec{ \rm{m}}$ , are:

$\begin{eqnarray} &&\vec{\Pi} = -p\vec{ \rm{I}}+{(\mu+ {\frac{1}{2}}k)(\nabla\vec{q}+\nabla^{T}\vec{q})}+{k}{\vec{\epsilon}}{\cdot(\vec{\omega}-\vec{\nu})}, \end{eqnarray}$

(4)

$\begin{eqnarray} &&\vec{ \rm{m}} = \alpha\vec{ \rm{I}}\cdot\nabla\vec{\nu}+{\beta\nabla\vec{\nu}}+{\gamma\nabla^{T}\vec{\nu}}, \end{eqnarray}$

(5)

where $\vec{ \rm{I}}$ is the unit dyadic, $\vec{\epsilon}$ is the unit triadic, $\vec{\omega} = {\frac{1}{2}}(\nabla\wedge\vec{q})$ is the vorticity vector, and $(\cdot)^T$ denotes a dyadic transposition. When $k = 0$ , the Eqs (1)–(5) reduce to Navier-Stokes' classical model ^[31].

3. Mathematical formulation

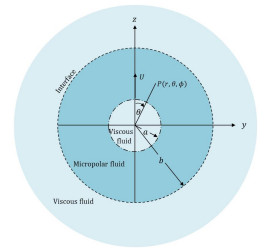
Assume a spherical interface separating two non-mixable fluids; one of them is bounded and the other is semi-unbounded. The fluid outside is a Newtonian fluid, whereas the fluid inside is a non-Newtonian fluid. A viscous sphere droplet of radius $a$ is embedded in a micropolar fluid, at which its centre coincides with the spherical interface centre, and the spherical interface of radius $b(b > a)$ . The viscous droplet sphere is moving with a uniform velocity $\vec{U} = U\vec{e}_{ \rm{z}}$ ; the drop's centre is instantaneously located at the centre of the interface, which is to be at rest; see . Geometrically, to describe the viscous sphere droplet and the spherical interface, it is appropriate to define the unit vectors $(\vec{e}_{r}, \vec{e}_{\theta}, \vec{e}_{\phi})$ that correspond to the spherical coordinates $(r, \theta, \phi)$ , and consider that the viscous droplet centre serves as the origin of this coordinate system. The gyro-inertial and inertial factors in the field equations may be ignored since it is assumed that the Reynolds numbers for the flow of the micropolar fluid are small enough. Therefore, we take the Stokesian approximation into consideration. The motion is generated by the movement of the viscous droplet in both fluid regions. All dynamical variables in this motion are independent of $\phi$ , and it is axially symmetric. Thus, for the three fluid phases, our approach involves utilising spherical coordinates to represent the velocity and microrotation components ^[3,31]:

$\begin{eqnarray} &&\vec{q}^{(1)} = q_{r}^{(1)}(r, \theta)\vec{e}_{r}+q_{\theta}^{(1)}(r, \theta)\vec{e}_{\theta}, \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\, \, r < a, \end{eqnarray}$

(6)

$\begin{eqnarray} &&\vec{q}^{(2)} = q_{r}^{(2)}(r, \theta)\vec{e}_{r}+q_{\theta}^{(2)}(r, \theta)\vec{e}_{\theta}\quad \text{and}\quad\vec{\nu}^{(2)} = \nu_{\phi}^{(2)}(r, \theta)\vec{e}_{\phi}, \quad\, a\leq\, r\leq\, b, \end{eqnarray}$

(7)

$\begin{eqnarray} &&\vec{q}^{(3)} = q_{r}^{(3)}(r, \theta)\vec{e}_{r}+q_{\theta}^{(3)}(r, \theta)\vec{e}_{\theta}, \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\, \, r > b. \end{eqnarray}$

(8)

Figure 1. Illustration of a viscous sphere droplet moving inside a concentric micropolar-viscous interface.

DownLoad: Full-Size Img PowerPoint

Let $\psi^{(1)}$ , $\psi^{(2)}$ , and $\psi^{(3)}$ refer to, respectively, the three stream functions for the three flow areas inside the viscous drop, between the surface of the drop and the micropolar-viscous interface, and outside the micropolar-viscous interface. Therefore, using the conservation of mass equation (1), in terms of stream functions, the velocity components in the three fluid areas may be expressed as

$\begin{eqnarray} &&q_{r}^{(1)} = \frac{1}{r^2}\frac{\partial\psi^{(1)}}{\partial \zeta}, \quad q_{\theta}^{(1)} = \frac{1}{r\sqrt{1-\zeta^{2}}}\frac{\partial\psi^{(1)}}{\partial r}, \end{eqnarray}$

(9)

$\begin{eqnarray} &&q_{r}^{(2)} = \frac{1}{r^2}\frac{\partial\psi^{(2)}}{\partial \zeta}, \quad q_{\theta}^{(2)} = \frac{1}{r\sqrt{1-\zeta^{2}}}\frac{\partial\psi^{(2)}}{\partial r}, \end{eqnarray}$

(10)

$\begin{eqnarray} &&q_{r}^{(3)} = \frac{1}{r^2}\frac{\partial\psi^{(3)}}{\partial \zeta}, \quad q_{\theta}^{(3)} = \frac{1}{r\sqrt{1-\zeta^{2}}}\frac{\partial\psi^{(3)}}{\partial r}, \end{eqnarray}$

(11)

where $\zeta = \cos\theta$ . Using the field Eqs (1)–(3) and the formulaes (6)–(8) with the velocity components (9)–(11), it is found that the following systems of equations exist in the three fluid regions:

For the viscous fluid in the domain $(r < a)$ :

$\begin{eqnarray} &&\frac{\partial\, p^{(1)}}{\partial\, r}+\frac{\mu_{1}}{r^2\sin\theta}\frac{\partial}{\partial\theta}(E^{2}\psi^{(1)}) = 0, \end{eqnarray}$

(12)

$\begin{eqnarray} &&\frac{1}{r}\frac{\partial\, p^{(1)}}{\partial\theta}-\frac{\mu_{1}}{r\sin\theta}\frac{\partial}{\partial\, r}(E^{2}\psi^{(1)}) = 0, \end{eqnarray}$

(13)

and for the micropolar fluid in the domain $(a\leq\, r\leq\, b)$ :

$\begin{eqnarray} &&\frac{\partial\, p^{(2)}}{\partial\, r}-\frac{k_{2}}{r\sin\theta}\frac{\partial}{\partial\theta}(\nu_{\phi}^{(2)}\sin\theta)+\frac{\mu_{2}+k_{2}}{r^2\sin\theta}\frac{\partial}{\partial\theta}(E^{2}\psi^{(2)}) = 0, \end{eqnarray}$

(14)

$\begin{eqnarray} &&\frac{1}{r}\frac{\partial\, p^{(2)}}{\partial\theta}+\frac{k_{2}}{r}\frac{\partial}{\partial\, r}(r\nu_{\phi}^{(2)})-\frac{\mu_{2}+k_{2}}{r\sin\theta}\frac{\partial}{\partial\, r}(E^{2}\psi^{(2)}) = 0, \end{eqnarray}$

(15)

$\begin{eqnarray} &&2k_{2}(\nu_{\phi}^{(2)}r\sin\theta)-\gamma_{2}E^{2}(\nu_{\phi}^{(2)}r\sin\theta)-k_{2}(E^{2}\psi^{(2)}) = 0, \end{eqnarray}$

(16)

and for the viscous fluid in the domain $(r > b)$ :

$\begin{eqnarray} &&\frac{\partial\, p^{(3)}}{\partial\, r}+\frac{\mu_{3}}{r^2\sin\theta}\frac{\partial}{\partial\theta}(E^{2}\psi^{(3)}) = 0, \end{eqnarray}$

(17)

$\begin{eqnarray} &&\frac{1}{r}\frac{\partial\, p^{(3)}}{\partial\theta}-\frac{\mu_{3}}{r\sin\theta}\frac{\partial}{\partial\, r}(E^{2}\psi^{(3)}) = 0, \end{eqnarray}$

(18)

where $\mu_{1}$ , $\mu_{2}$ , and $\mu_{3}$ are the viscosity coefficients for the viscous fluid inside the drop, between the surface of the drop and the micropolar-viscous interface, and outside the micropolar-viscous interface, respectively, and the axisymmetric Stokesian operator is defined by

$\begin{equation*} E^{2} = \frac{\partial^{2}}{\partial\, r^{2}}+\frac{1}{r^{2}}\frac{\partial^{2}}{\partial\theta^{2}}-\frac{\cot\theta}{r^{2}}\frac{\partial}{\partial\theta}. \end{equation*}$

Now, after removing the formulaes $p^{(1)}$ , $p^{(2)}$ , $p^{(3)}$ , and $\nu_{\phi}^{(2)}$ from Eqs (12)–(18), we find that three differential equations are satisfied by the three stream functions, which are as follows:

$\begin{eqnarray} &&E^{4}\psi^{(1)} = 0, \quad\quad\quad\quad\quad\, r < a, \end{eqnarray}$

(19)

$\begin{eqnarray} &&E^{4}(E^{2}-\ell_{2}^{2})\psi^{(2)} = 0, \quad\ell_{2}^{2} = k_{2}(2\mu_{2}+k_{2})/(\gamma_{2}(\mu_{2}+k_{2})), \quad\, a\leq\, r\leq\, b, \end{eqnarray}$

(20)

$\begin{eqnarray} &&E^{4}\psi^{(3)} = 0, \quad\quad\quad\quad\quad\, r > b. \end{eqnarray}$

(21)

Also, we may obtain the component of the microrotation $\nu_{\phi}^{(2)}$ for the micropolar fluid from the following relation:

$\begin{equation} \nu_{\phi}^{(2)} = \frac{1}{2r\sin\theta}\big{(}E^{2}\psi_{1}+2m_{2}\ell_{2}^{2}\psi_{2}\big{)}, \end{equation}$

(22)

where $m_{2} = (\mu_{2}+k_{2})/k_{2}$ , $\psi^{(2)} = \psi_{1}+\psi_{2}$ , $E^{4}\psi_{1} = 0$ , and $E^{2}\psi_{2} = \ell_{2}^{2}\psi_{2}$ .

Also, we may obtain the vorticity components $\omega_{\phi}^{(1)}(\vec{\omega}^{(1)} = \omega_{\phi}^{(1)}(r, \theta)\vec{e}_{\phi})$ and $\omega_{\phi}^{(3)}(\vec{\omega}^{(3)} = \omega_{\phi}^{(3)}(r, \theta)\vec{e}_{\phi})$ , for the viscous fluid phases from the relations

$\begin{eqnarray} \omega_{\phi}^{(1)}& = & {\frac{1}{2}}\big{(}\nabla\wedge\vec{q}^{(1)}\big{)}\cdot\vec{e}_{\phi}, \end{eqnarray}$

(23)

$\begin{eqnarray} \omega_{\phi}^{(3)}& = & {\frac{1}{2}}\big{(}\nabla\wedge\vec{q}^{(3)}\big{)}\cdot\vec{e}_{\phi}. \end{eqnarray}$

(24)

It is also essential to specify the boundary circumstances in order to solve the differential equations (19)–(21).

As stated before, the droplet surface and the micropolar-viscous interface are presumed to be stationary spherical interfaces. This assumption is physically valid since the interface stays spherical due to the surface tension at the interface, which separates two non-miscible fluids, even when subjected to shearing stresses that deform it. In the beginning, at least, the droplet will be approximately spherical if the motion is sufficiently slow ^[31]. Therefore, in this study, we assume that the deformation of the droplet surface and the micropolar-viscous interface are neglected and that the interfaces keep their spherical shapes permanently. Therefore, because there is no mass transfer across the two separating interfaces, the components of the normal velocity on the two sides at the two separating surfaces ought to disappear, and both the tangential stresses and the tangential velocity components are continuous. Since the micropolar fluid phase contains a microstructure, there is also a condition on the microrotation component. Moreover, under these circumstances, the convenient physical one is that the microrotation for the micropolar fluid on the drop's surface and at the micropolar-viscous interface is in proportion to the vorticity for the viscous fluid ^[25]. Here, the proportionality coefficient, $s$ , could be known as the spin parameter. The range of this parameter, which is zero to one, is presumed to depend only on the nature of the fluids on both sides of the interface. First value: When the micro-elements near a stiff boundary are incapable of rotating, the situation is represented by $s = 0$ (no spin). Second value: When the microrotation of the micro-elements equals the vorticity of the viscous fluid at the boundary, the situation is represented by $s = 1$ . Moreover, for away from the external interface, the velocity and microrotation components must vanish, and at the centre of the internal interface sphere, the velocity components must exist.

The physical boundary conditions mentioned above have the following mathematical formulation:

$\begin{eqnarray} At\, \, \, r = a:\quad\, &&q_{r}^{(2)} = q_{r}^{(1)}, \end{eqnarray}$

(25)

$\begin{eqnarray} &&q_{r}^{(2)} = U\cos\theta, \end{eqnarray}$

(26)

$\begin{eqnarray} &&q_{\theta}^{(2)} = q_{\theta}^{(1)}, \end{eqnarray}$

(27)

$\begin{eqnarray} &&t_{r\theta}^{(2)} = t_{r\theta}^{(1)}, \end{eqnarray}$

(28)

$\begin{eqnarray} &&\nu_{\phi}^{(2)} = s_{1}\omega_{\phi}^{(1)}, \end{eqnarray}$

(29)

$\begin{eqnarray} &&\lim\limits_{r\to\, 0}q_{r}^{(1)}, \quad\lim\limits_{r\to\, 0}q_{\theta}^{(1)}\quad\text{exist}, \end{eqnarray}$

(30)

$\begin{eqnarray} At\, \, \, r = b:\quad\, &&q_{r}^{(2)} = q_{r}^{(3)} = 0, \end{eqnarray}$

(31)

$\begin{eqnarray} &&q_{\theta}^{(2)} = q_{\theta}^{(3)}, \end{eqnarray}$

(32)

$\begin{eqnarray} &&t_{r\theta}^{(2)} = t_{r\theta}^{(3)}, \end{eqnarray}$

(33)

$\begin{eqnarray} &&\nu_{\phi}^{(2)} = s_{3}\omega_{\phi}^{(3)}, \end{eqnarray}$

(34)

$\begin{eqnarray} &&\lim\limits_{r\to\infty}q_{r}^{(3)}, \quad\lim\limits_{r\to\infty}q_{\theta}^{(3)}\quad\text{vanish}, \end{eqnarray}$

(35)

where $s_{1}$ and $s_{3}$ are the spin parameters inside the viscous drop and outside the micropolar-viscous interface, respectively. $t_{r\theta}^{(1)}$ , $t_{r\theta}^{(2)}$ , and $t_{r\theta}^{(3)}$ are the shear stresses for the flow inside the droplet, between the surface of the drop and the micropolar-viscous interface, and outside the micropolar-viscous interface, respectively.

The solutions of Eqs (19)–(21) suitable for satisfying boundary conditions (25)–(35) for the stream functions are respectively presented by:

$\begin{eqnarray} \psi^{(1)} & = & {\frac{1}{2}}(A_{1}r^{2}+B_{1}r^{4})\sin^{2}\theta, \end{eqnarray}$

(36)

$\begin{eqnarray} \psi^{(2)} & = & {\frac{1}{2}}\big{(}A_{2}r^{2}+B_{2}r^{4}+C_{2}r^{-1}+D_{2}r+E_{2}\sqrt{r}I_{\frac{3}{2}}(\ell_{2}r)+F_{2}\sqrt{r}K_{\frac{3}{2}}(\ell_{2}r)\big{)}\sin^{2}\theta, \end{eqnarray}$

(37)

$\begin{eqnarray} \psi^{(3)} & = & {\frac{1}{2}}(A_{3}r^{-1}+B_{3}r)\sin^{2}\theta, \end{eqnarray}$

(38)

where $I_{\frac{3}{2}}(\cdot)$ and $K_{\frac{3}{2}}(\cdot)$ are respectively the first and second kind for modified Bessel functions of order ${\frac{3}{2}}$ , and $A_{1}$ , $B_{1}$ , $A_{2}$ , $B_{2}$ , $C_{2}$ , $D_{2}$ , $E_{2}$ , $F_{2}$ , $A_{3}$ , and $B_{3}$ are unknown constants.

To satisfy the boundary conditions (28) and (33), the following formulaes, in spherical coordinates, for the shear stresses $t_{r\theta}^{(1)}$ , $t_{r\theta}^{(2)}$ , and $t_{r\theta}^{(3)}$ are given by:

$\begin{eqnarray} &&t_{r\theta}^{(1)} = \mu_{1}\bigg{(}\frac{1}{r}\frac{\partial\, q_{r}^{(1)}}{\partial\theta}+r\frac{\partial}{\partial\, r}\frac{q_{\theta}^{(1)}}{r}-\frac{1}{r}q_{\theta}^{(1)}\bigg{)}, \end{eqnarray}$

(39)

$\begin{eqnarray} &&t_{r\theta}^{(2)} = \frac{1}{2}(2\mu_{2}+k_{2})\bigg{(}\frac{1}{r}\frac{\partial\, q_{r}^{(2)}}{\partial\theta}+r\frac{\partial}{\partial\, r}\frac{q_{\theta}^{(2)}}{r}-\frac{1}{r}q_{\theta}^{(2)}\bigg{)}+k_{2}\bigg{(}\frac{1}{2r}\bigg{(}\frac{\partial}{\partial\, r}rq_{\theta}^{(2)}-\frac{\partial\, q_{r}^{(2)}}{\partial\theta}\bigg{)}-\nu_{\phi}^{(2)}\bigg{)}, \\ \end{eqnarray}$

(40)

$\begin{eqnarray} &&t_{r\theta}^{(3)} = \mu_{3}\bigg{(}\frac{1}{r}\frac{\partial\, q_{r}^{(3)}}{\partial\theta}+r\frac{\partial}{\partial\, r}\frac{q_{\theta}^{(3)}}{r}-\frac{1}{r}q_{\theta}^{(3)}\bigg{)}. \end{eqnarray}$

(41)

Therefore, the formulaes for the velocity components, the shear stresses, the vorticity components, and the microrotation component in the three fluid regions are given by

$\begin{eqnarray} &&q_{r}^{(1)} = -(A_{1}+B_{1}r^{2})\cos\theta, \end{eqnarray}$

(42)

$\begin{eqnarray} &&q_{\theta}^{(1)} = (A_{1}+2B_{1}r^{2})\sin\theta, \end{eqnarray}$

(43)

$\begin{eqnarray} &&t_{r\theta}^{(1)} = 3\mu_{1}B_{1}r\sin\theta, \end{eqnarray}$

(44)

$\begin{eqnarray} &&\omega_{\phi}^{(1)} = {\frac{5}{2}}B_{1}r\sin\theta, \end{eqnarray}$

(45)

$\begin{eqnarray} &&q_{r}^{(2)} = -\big{(}A_{2}+B_{2}r^{2}+C_{2}r^{-3}+D_{2}r^{-1}+E_{2}r^{-\frac{3}{2}}I_{\frac{3}{2}}(\ell_{2}r)+F_{2}r^{-\frac{3}{2}}K_{\frac{3}{2}}(\ell_{2}r)\big{)}\cos\theta, \end{eqnarray}$

(46)

$\begin{eqnarray} &&q_{\theta}^{(2)} = {\frac{1}{2}}\big{(}2A_{2}+4B_{2}r^{2}-C_{2}r^{-3}+D_{2}r^{-1}+E_{2}r^{-\frac{3}{2}}\big{(}\ell_{2}rI_{\frac{1}{2}}(\ell_{2}r)-I_{\frac{3}{2}}(\ell_{2}r)\big{)}\\ &&\qquad\quad-F_{2}r^{-\frac{3}{2}}\big{(}\ell_{2}rK_{\frac{1}{2}}(\ell_{2}r)+K_{\frac{3}{2}}(\ell_{2}r)\big{)}\big{)}\sin\theta, \end{eqnarray}$

(47)

$\begin{eqnarray} &&t_{r\theta}^{(2)} = {\frac{1}{2}}(2\mu_{2}+k_{2})\big{(}3B_{2}r+3C_{2}r^{-4}+E_{2}r^{-\frac{5}{2}}\big{(}3I_{\frac{3}{2}}(\ell_{2}r)-\ell_{2}rI_{\frac{1}{2}}(\ell_{2}r)\big{)}\\ &&\qquad\qquad+F_{2}r^{-\frac{5}{2}}\big{(}3K_{\frac{3}{2}}(\ell_{2}r)+\ell_{2}rK_{\frac{1}{2}}(\ell_{2}r)\big{)}\big{)}\sin\theta, \end{eqnarray}$

(48)

$\begin{eqnarray} &&\nu_{\phi}^{(2)} = {\frac{1}{2}}\big{(}5B_{2}r-D_{2}r^{-2}+m_{2}\ell_{2}^{2}E_{2}r^{-\frac{1}{2}}I_{\frac{3}{2}}(\ell_{2}r)+m_{2}\ell_{2}^{2}F_{2}r^{-\frac{1}{2}}K_{\frac{3}{2}}(\ell_{2}r)\big{)}\sin\theta, \end{eqnarray}$

(49)

$\begin{eqnarray} &&q_{r}^{(3)} = -(A_{3}r^{-3}+B_{3}r^{-1})\cos\theta, \end{eqnarray}$

(50)

$\begin{eqnarray} &&q_{\theta}^{(3)} = - {\frac{1}{2}}(A_{3}r^{-3}-B_{3}r^{-1})\sin\theta, \end{eqnarray}$

(51)

$\begin{eqnarray} &&t_{r\theta}^{(3)} = 3\mu_{3}A_{3}r^{-4}\sin\theta, \end{eqnarray}$

(52)

$\begin{eqnarray} &&\omega_{\phi}^{(3)} = {\frac{1}{2}}(2A_{3}r^{-4}+B_{3}r^{-2})\sin\theta. \end{eqnarray}$

(53)

Inserting formulations (42)–(53) into conditions (25)–(29) and (31)–(34), we can derive a finite set of ten linear equations for figuring out the unknown constants $A_{1}$ , $B_{1}$ , $A_{2}$ , $B_{2}$ , $C_{2}$ , $D_{2}$ , $E_{2}$ , $F_{2}$ , $A_{3}$ , and $B_{3}$ :

$\begin{eqnarray} &&A_{1}+B_{1}a^{2}-A_{2}-B_{2}a^{2}-C_{2}a^{-3}-D_{2}a^{-1}-E_{2}a^{-\frac{3}{2}}I_{\frac{3}{2}}(\ell_{2}a)-F_{2}a^{-\frac{3}{2}}K_{\frac{3}{2}}(\ell_{2}a) = 0, \\ \end{eqnarray}$

(54)

$\begin{eqnarray} &&A_{2}+B_{2}a^{2}+C_{2}a^{-3}+D_{2}a^{-1}+E_{2}a^{-\frac{3}{2}}I_{\frac{3}{2}}(\ell_{2}a)+F_{2}a^{-\frac{3}{2}}K_{\frac{3}{2}}(\ell_{2}a) = -U, \end{eqnarray}$

(55)

$\begin{eqnarray} &&2A_{1}+4B_{1}a^{2}-2A_{2}-4B_{2}a^{2}+C_{2}a^{-3}-D_{2}a^{-1}-E_{2}a^{-\frac{3}{2}}\big{(}\ell_{2}aI_{\frac{1}{2}}(\ell_{2}a)-I_{\frac{3}{2}}(\ell_{2}a)\big{)}\\ &&\quad+F_{2}a^{-\frac{3}{2}}\big{(}\ell_{2}aK_{\frac{1}{2}}(\ell_{2}a)+K_{\frac{3}{2}}(\ell_{2}a)\big{)} = 0, \end{eqnarray}$

(56)

$\begin{eqnarray} &&-3\lambda_{12}B_{1}a^{2}+3B_{2}a^{2}+3C_{2}a^{-3}+E_{2}a^{-\frac{3}{2}}\big{(}3I_{\frac{3}{2}}(\ell_{2}a)-\ell_{2}aI_{\frac{1}{2}}(\ell_{2}a)\big{)}\\ &&\quad+F_{2}a^{-\frac{3}{2}}\big{(}3K_{\frac{3}{2}}(\ell_{2}a)+\ell_{2}aK_{\frac{1}{2}}(\ell_{2}a)\big{)} = 0, \end{eqnarray}$

(57)

$\begin{eqnarray} &&-5s_{1}B_{1}a^{2}+5B_{2}a^{2}-D_{2}a^{-1}+m_{2}\ell_{2}^{2}E_{2}a^{\frac{1}{2}}I_{\frac{3}{2}}(\ell_{2}a)+m_{2}\ell_{2}^{2}F_{2}a^{\frac{1}{2}}K_{\frac{3}{2}}(\ell_{2}a) = 0, \end{eqnarray}$

(58)

$\begin{eqnarray} &&A_{2}+B_{2}b^{2}+C_{2}b^{-3}+D_{2}b^{-1}+E_{2}b^{-\frac{3}{2}}I_{\frac{3}{2}}(\ell_{2}b)+F_{2}b^{-\frac{3}{2}}K_{\frac{3}{2}}(\ell_{2}b) = 0, \end{eqnarray}$

(59)

$\begin{eqnarray} &&A_{3}+B_{3}b^{2} = 0, \end{eqnarray}$

(60)

$\begin{eqnarray} &&2A_{2}+4B_{2}b^{2}-C_{2}b^{-3}+D_{2}b^{-1}+E_{2}b^{-\frac{3}{2}}\big{(}\ell_{2}bI_{\frac{1}{2}}(\ell_{2}b)-I_{\frac{3}{2}}(\ell_{2}b)\big{)}\\ &&\quad-F_{2}b^{-\frac{3}{2}}\big{(}\ell_{2}bK_{\frac{1}{2}}(\ell_{2}b)+K_{\frac{3}{2}}(\ell_{2}b)\big{)}+A_{3}b^{-3}-B_{3}b^{-1} = 0, \end{eqnarray}$

(61)

$\begin{eqnarray} &&3B_{2}b^{2}+3C_{2}b^{-3}+E_{2}b^{-\frac{3}{2}}\big{(}3I_{\frac{3}{2}}(\ell_{2}b)-\ell_{2}bI_{\frac{1}{2}}(\ell_{2}b)\big{)}+F_{2}b^{-\frac{3}{2}}\big{(}3K_{\frac{3}{2}}(\ell_{2}b)+\ell_{2}bK_{\frac{1}{2}}(\ell_{2}b)\big{)}\\ &&\quad-3\lambda_{32}A_{3}b^{-3} = 0, \end{eqnarray}$

(62)

$\begin{eqnarray} &&5B_{2}b^{2}-D_{2}b^{-1}+m_{2}\ell_{2}^{2}E_{2}b^{\frac{1}{2}}I_{\frac{3}{2}}(\ell_{2}b)+m_{2}\ell_{2}^{2}F_{2}b^{\frac{1}{2}}K_{\frac{3}{2}}(\ell_{2}b)-2s_{3}A_{3}b^{-3}-s_{3}B_{3}b^{-1} = 0, \\ \end{eqnarray}$

(63)

where $\lambda_{12} = 2\mu_{12}/(2+k_{2}/\mu_{2})$ and $\lambda_{32} = 2\mu_{32}/(2+k_{2}/\mu_{2})$ with $\mu_{12} = \mu_{1}/\mu_{2}$ and $\mu_{32} = \mu_{3}/\mu_{2}$ . Here, $\mu_{12}$ represents the ratio of dynamic viscosity coefficients between the outer and inner fluids to the droplet, and $\mu_{32}$ represents the ratio of dynamic viscosity coefficients between the inner and outer fluids to the micropolar-viscous interface. As $\mu_{12}\to\infty$ , the droplet becomes a solid sphere, whereas as $\mu_{12}\to\, 0$ , the droplet becomes a gas bubble; on the other hand, as $\mu_{32}\to\infty$ , the micropolar-viscous interface becomes a cavity wall (solid wall), whereas as $\mu_{32}\to\, 0$ , the fluid outside the micropolar-viscous interface becomes a gas (air), see Figure 2.

Figure 2. Geometric sketch of a spherical viscous droplet inside a micropolar-viscous interface.

DownLoad: Full-Size Img PowerPoint

The normalised hydrodynamic drag force $F_{z}$ made by the micropolar fluid on the viscous droplet's surface in the presence of the micropolar-viscous interface is shown to be ^[23,32]

$\begin{equation} F_{z} = 4\pi(2\mu_{2}+k_{2})lim_{r\to\infty}\frac{\psi^{(2)}}{r\sin^{2}\theta} = 2\pi(2\mu_{2}+k_{2})D_{2}, \end{equation}$

(64)

Here, the expression (64) demonstrates that the normalised hydrodynamic drag force applied to the viscous sphere droplet relies solely on the coefficient $D_{2}$ , which can be obtained by solving the system of ten Eqs (54)–(63) using the Gaussian elimination method. To provide some comparison, the normalised hydrodynamic drag force $F_{z\infty}$ made by an infinite micropolar fluid on the viscous droplet's surface is found to be ^[30]

$\begin{equation} F_{z\infty} = -\frac{6\pi\, Ua(2\mu_{2}+k_{2})(\mu_{2}+k_{2})(\ell_{2}a+1)(3\lambda_{12}+2)}{6(\mu_{2}+k_{2})(\lambda_{12}+1)(\ell_{2}a+1)-k_{2}(3\lambda_{12}+2-5s_{1})}. \end{equation}$

(65)

The micropolar-viscous interface correction factor $K$ , with the aid of Eqs (64) and (65), is defined as

$\begin{equation} K = \frac{F_{z}}{F_{z\infty}}. \end{equation}$

(66)

4. The case for the effect of a viscous-micropolar interface on a viscous sphere droplet

Here, in this segment, we suppose the opposite scenario (see ), that is, a viscous sphere droplet is submerged in a viscous fluid of viscosity $\hat{\mu}_{2}$ . Let $\hat{\mu}_{1}$ and $\hat{\mu}_{3}$ represent the viscosity coefficients of the viscous inside the drop and the micropolar outside the viscous-micropolar interface, respectively. Therefore, the stream functions of the fluids in the three regions satisfy the differential equations, as follows:

$\begin{eqnarray} &&E^{4}\hat{\psi}^{(1)} = 0, \quad\quad\quad\quad\quad\, r < a, \end{eqnarray}$

(67)

$\begin{eqnarray} &&E^{4}\hat{\psi}^{(2)} = 0, \quad\quad\quad\quad\quad\, a\leq\, r\leq\, b, \end{eqnarray}$

(68)

$\begin{eqnarray} &&E^{4}(E^{2}-\ell_{3}^{2})\hat{\psi}^{(3)} = 0, \quad\ell_{3}^{2} = k_{3}(2\hat{\mu}_{3}+k_{3})/(\gamma_{3}(\hat{\mu}_{3}+k_{3})), \quad\, r > b. \end{eqnarray}$

(69)

Figure 3. Illustration of a viscous sphere droplet moving inside a concentric viscous-micropolar interface.

DownLoad: Full-Size Img PowerPoint

The following are the general solutions to Eqs (67)–(69):

$\begin{eqnarray} \hat{\psi}^{(1)} & = & {\frac{1}{2}}(\hat{A}_{1}r^{2}+\hat{B}_{1}r^{4})\sin^{2}\theta, \end{eqnarray}$

(70)

$\begin{eqnarray} \hat{\psi}^{(2)} & = & {\frac{1}{2}}(\hat{A}_{2}r^{2}+\hat{B}_{2}r^{4}+\hat{C}_{2}r^{-1}+\hat{D}_{2}r)\sin^{2}\theta, \end{eqnarray}$

(71)

$\begin{eqnarray} \hat{\psi}^{(3)} & = & {\frac{1}{2}}\big{(}\hat{A}_{3}r^{-1}+\hat{B}_{3}r+\hat{C}_{3}\sqrt{r}K_{\frac{3}{2}}(\ell_{3}r)\big{)}\sin^{2}\theta, \end{eqnarray}$

(72)

where $\hat{A}_{1}$ , $\hat{B}_{1}$ , $\hat{A}_{2}$ , $\hat{B}_{2}$ , $\hat{C}_{2}$ , $\hat{D}_{2}$ , $\hat{A}_{3}$ , $\hat{B}_{3}$ , and $\hat{C}_{3}$ are unknown constants.

In this case, the boundary conditions roughly take the same form as the boundary conditions (25)–(35), as follows:

$\begin{eqnarray} At\, \, \, r = a:\quad\, &&\hat{q}_{r}^{(2)} = \hat{q}_{r}^{(1)}, \end{eqnarray}$

(73)

$\begin{eqnarray} &&\hat{q}_{r}^{(2)} = U\cos\theta, \end{eqnarray}$

(74)

$\begin{eqnarray} &&\hat{q}_{\theta}^{(2)} = \hat{q}_{\theta}^{(1)}, \end{eqnarray}$

(75)

$\begin{eqnarray} &&\hat{t}_{r\theta}^{(2)} = \hat{t}_{r\theta}^{(1)}, \end{eqnarray}$

(76)

$\begin{eqnarray} &&\lim\limits_{r\to\, 0}\hat{q}_{r}^{(1)}, \quad\lim\limits_{r\to\, 0}\hat{q}_{\theta}^{(1)}\quad\text{exist}, \end{eqnarray}$

(77)

$\begin{eqnarray} At\, \, \, r = b:\quad\, &&\hat{q}_{r}^{(2)} = \hat{q}_{r}^{(3)} = 0, \end{eqnarray}$

(78)

$\begin{eqnarray} &&\hat{q}_{\theta}^{(2)} = \hat{q}_{\theta}^{(3)}, \end{eqnarray}$

(79)

$\begin{eqnarray} &&\hat{t}_{r\theta}^{(2)} = \hat{t}_{r\theta}^{(3)}, \end{eqnarray}$

(80)

$\begin{eqnarray} &&s_{2}\hat{\omega}_{\phi}^{(2)} = \hat{\nu}_{\phi}^{(3)}, \end{eqnarray}$

(81)

$\begin{eqnarray} &&\lim\limits_{r\to\infty}\hat{q}_{r}^{(3)}, \quad\lim\limits_{r\to\infty}\hat{q}_{\theta}^{(3)}, \quad\lim\limits_{r\to\infty}\hat{\nu}_{\phi}^{(3)}\quad\text{vanish}, \end{eqnarray}$

(82)

where $s_{2}$ is the spin parameter for the viscous fluid outside the droplet's surface and inside the viscous-micropolar interface.

Therefore, the formulaes for the velocity components, the shear stresses, the vorticity component, and the microrotation component in the three fluid regions are given by

$\begin{eqnarray} &&\hat{q}_{r}^{(1)} = -(\hat{A}_{1}+\hat{B}_{1}r^{2})\cos\theta, \end{eqnarray}$

(83)

$\begin{eqnarray} &&\hat{q}_{\theta}^{(1)} = (\hat{A}_{1}+2\hat{B}_{1}r^{2})\sin\theta, \end{eqnarray}$

(84)

$\begin{eqnarray} &&\hat{t}_{r\theta}^{(1)} = 3\hat{\mu}_{1}\hat{B}_{1}r\sin\theta, \end{eqnarray}$

(85)

$\begin{eqnarray} &&\hat{q}_{r}^{(2)} = -(\hat{A}_{2}+\hat{B}_{2}r^{2}+\hat{C}_{2}r^{-3}+\hat{D}_{2}r^{-1})\cos\theta, \end{eqnarray}$

(86)

$\begin{eqnarray} &&\hat{q}_{\theta}^{(2)} = {\frac{1}{2}}(2\hat{A}_{2}+4\hat{B}_{2}r^{2}-\hat{C}_{2}r^{-3}+\hat{D}_{2}r^{-1})\sin\theta, \end{eqnarray}$

(87)

$\begin{eqnarray} &&\hat{t}_{r\theta}^{(2)} = 3\hat{\mu}_{2}(\hat{B}_{2}r+\hat{C}_{2}r^{-4})\sin\theta, \end{eqnarray}$

(88)

$\begin{eqnarray} &&\hat{\omega}_{\phi}^{(2)} = {\frac{1}{2}}(2\hat{A}_{2}r^{-1}+7\hat{B}_{2}r+2\hat{C}_{2}r^{-4}+\hat{D}_{2}r^{-2})\sin\theta, \end{eqnarray}$

(89)

$\begin{eqnarray} &&\hat{q}_{r}^{(3)} = -\big{(}\hat{A}_{3}r^{-3}+\hat{B}_{3}r^{-1}+\hat{C}_{3}r^{-\frac{3}{2}}K_{\frac{3}{2}}(\ell_{3}r)\big{)}\cos\theta, \end{eqnarray}$

(90)

$\begin{eqnarray} &&\hat{q}_{\theta}^{(3)} = - {\frac{1}{2}}\big{(}\hat{A}_{3}r^{-3}-\hat{B}_{3}r^{-1}+\hat{C}_{3}r^{-\frac{3}{2}}\big{(}\ell_{3}rK_{\frac{1}{2}}(\ell_{3}r)+K_{\frac{3}{2}}(\ell_{3}r)\big{)}\big{)}\sin\theta, \end{eqnarray}$

(91)

$\begin{eqnarray} &&\hat{t}_{r\theta}^{(3)} = {\frac{1}{2}}(2\hat{\mu}_{3}+k_{3})\big{(}3\hat{A}_{3}r^{-4}+\hat{C}_{3}r^{-\frac{5}{2}}\big{(}3K_{\frac{3}{2}}(\ell_{3}r)+\ell_{3}rK_{\frac{1}{2}}(\ell_{3}r)\big{)}\big{)}\sin\theta, \end{eqnarray}$

(92)

$\begin{eqnarray} &&\hat{\nu}_{\phi}^{(3)} = - {\frac{1}{2}}\big{(}\hat{B}_{3}r^{-2}-m_{3}\ell_{3}^{2}\hat{C}_{3}r^{-\frac{1}{2}}K_{\frac{3}{2}}(\ell_{3}r)\big{)}\sin\theta, \end{eqnarray}$

(93)

where $m_{3} = (\hat{\mu}_{3}+k_{3})/k_{3}$ .

Again, inserting formulaes (83)–(93) into conditions (73)–(76) and (78)–(81), we can derive a finite set of nine linear equations for figuring out the unknown constants $\hat{A}_{1}$ , $\hat{B}_{1}$ , $\hat{}A_{2}$ , $\hat{B}_{2}$ , $\hat{C}_{2}$ , $\hat{D}_{2}$ , $\hat{A}_{3}$ , $\hat{B}_{3}$ , and $\hat{C}_{3}$ :

$\begin{eqnarray} &&\hat{A}_{1}+\hat{B}_{1}a^{2}-\hat{A}_{2}-\hat{B}_{2}a^{2}-\hat{C}_{2}a^{-3}-\hat{D}_{2}a^{-1} = 0, \end{eqnarray}$

(94)

$\begin{eqnarray} &&\hat{A}_{2}+\hat{B}_{2}a^{2}+\hat{C}_{2}a^{-3}+\hat{D}_{2}a^{-1} = -U, \end{eqnarray}$

(95)

$\begin{eqnarray} &&2\hat{A}_{1}+4\hat{B}_{1}a^{2}-2\hat{A}_{2}-4\hat{B}_{2}a^{2}+\hat{C}_{2}a^{-3}-\hat{D}_{2}a^{-1} = 0, \end{eqnarray}$

(96)

$\begin{eqnarray} &&\hat{B}_{1}a^{2}-\mu_{21}\hat{B}_{2}a^{2}-\mu_{21}\hat{C}_{2}a^{-3} = 0, \end{eqnarray}$

(97)

$\begin{eqnarray} &&\hat{A}_{2}+\hat{B}_{2}b^{2}+\hat{C}_{2}b^{-3}+\hat{D}_{2}b^{-1} = 0, \end{eqnarray}$

(98)

$\begin{eqnarray} &&\hat{A}_{3}b^{-3}+\hat{B}_{3}b^{-1}+\hat{C}_{3}b^{-\frac{3}{2}}K_{\frac{3}{2}}(\ell_{3}b) = 0, \end{eqnarray}$

(99)

$\begin{eqnarray} &&2\hat{A}_{2}+4\hat{B}_{2}b^{2}-\hat{C}_{2}b^{-3}+\hat{D}_{2}b^{-1}+\hat{A}_{3}b^{-3}-\hat{B}_{3}b^{-1}+\hat{C}_{3}b^{-\frac{3}{2}}\big{(}\ell_{3}bK_{\frac{1}{2}}(\ell_{3}b)+K_{\frac{3}{2}}(\ell_{3}b)\big{)} = 0, \\ \end{eqnarray}$

(100)

$\begin{eqnarray} &&3\lambda_{23}\hat{B}_{2}b^{2}+3\lambda_{23}\hat{C}_{2}b^{-3}-3\hat{A}_{3}b^{-3}-\hat{C}_{3}b^{-\frac{3}{2}}\big{(}3K_{\frac{3}{2}}(\ell_{3}b)+\ell_{3}bK_{\frac{1}{2}}(\ell_{3}b)\big{)} = 0, \end{eqnarray}$

(101)

$\begin{eqnarray} &&2s_{2}\hat{A}_{2}+7s_{2}\hat{B}_{2}b^{2}+2s_{2}\hat{C}b^{-3}+s_{2}\hat{D}_{2}b^{-1}+\hat{B}_{3}b^{-1}-m_{3}\ell_{3}^{2}\hat{C}_{3}b^{\frac{1}{2}}K_{\frac{3}{2}}(\ell_{3}b) = 0, \end{eqnarray}$

(102)

where $\lambda_{23} = 2\mu_{23}/(2+k_{3}/\hat{\mu}_{3})$ with $\mu_{23} = \hat{\mu}_{2}/\hat{\mu}_{3}$ and $\mu_{21} = \hat{\mu}_{2}/\hat{\mu}_{1}$ . Here, $\mu_{23}$ represents the ratio of dynamic viscosity coefficients between the inner and outer fluids to the viscous-micropolar interface, and $\mu_{21}$ represents the ratio of dynamic viscosity coefficients between the outer and inner fluids to the droplet. As $\mu_{23}\to\infty$ , the fluid outside the viscous-micropolar interface becomes a gas (air), while as $\mu_{23}\to\, 0$ , the viscous-micropolar interface becomes a cavity wall (solid wall); on the other hand, as $\mu_{21}\to\infty$ , the droplet becomes a gas bubble, while as $\mu_{21}\to\, 0$ , the droplet becomes a solid sphere, see Figure 4.

Figure 4. Geometric sketch of a spherical viscous droplet inside a viscous-micropolar interface.

DownLoad: Full-Size Img PowerPoint

The normalised hydrodynamic drag force $\hat{F}_{z}$ made by the viscous fluid on the viscous droplet's surface in the presence of the viscous-micropolar interface is shown to be ^[31]

$\begin{equation} \hat{F}_{z} = 8\pi\hat{\mu}_{2}lim_{r\to\infty}\frac{\hat{\psi}^{(2)}}{r\sin^{2}\theta} = 4\pi\hat{\mu}_{2}\hat{D}_{2}, \end{equation}$

(103)

Here, the expression (103) demonstrates that the normalised hydrodynamic drag force applied to the viscous sphere droplet relies solely on the coefficient $\hat{D}_{2}$ , which can be obtained by solving the system of nine Eqs (94)–(102) using the Gaussian elimination method. To provide some comparison, the normalised hydrodynamic drag force $\hat{F}_{z\infty}$ made by an infinite viscous fluid on the viscous droplet's surface is found to be

$\begin{equation} \hat{F}_{z\infty} = -6\pi\, Ua\hat{\mu}_{2}\times\frac{2\hat{\mu}_{2}+3\hat{\mu}_{1}}{3\hat{\mu}_{2}+3\hat{\mu}_{1}}. \end{equation}$

(104)

The viscous-micropolar interface correction factor $\hat{K}$ , with the aid of equations (103) and (104), is defined as

$\begin{equation} \hat{K} = \frac{\hat{F}_{z}}{\hat{F}_{z\infty}}. \end{equation}$

(105)

5. Numerical outcomes and discussion

In this segment, we indicate the numerical outcomes of the factors $K$ and $\hat{K}$ that operate on a viscous sphere drop embedded in a micropolar or viscous fluid. These outcomes are exhibited in Figures 5–8 and – for a set of values: The spacing ratio $a/b$ , the viscosity ratios $(\mu_{12}, \mu_{32}, \mu_{21}, \mu_{23})$ , the spin parameters $(s_{1}, s_{2}, s_{3})$ , the micropolarity parameters $(k_{2}/\mu_{2}, k_{3}/\hat{\mu}_{3})$ , and the parameters $(\gamma_{2}/\mu_{2}a^{2}, \gamma_{3}/\hat{\mu}_{3}a^{2})$ . The method of Gaussian elimination is utilised to solve the set of linear Eqs (54)–(63) and (94)–(102) to get the desired unkowns, after utilising the suitable non-dimensional quantities. Thus, the drag force $K$ and $\hat{K}$ can be calculated.

Figure 5. Illustrations for

$K$ and

$\hat{K}$ towards the spacing ratio

$a/b$ for

$(a)$ a set of values of

$\mu_{32}$ with

$\mu_{12}\to\infty$ ,

$s_{1} = s_{3} = 0.2$ ,

$\gamma_{2}/\mu_{2}a^{2} = 0.3$ ,

$k_{2}/\mu_{2} = 3$ ;

$(b)$ a set of values of

$\mu_{23}$ with

$\mu_{21}\to\, 0$ ,

$s_{2} = 0.2$ ,

$\gamma_{3}/\hat{\mu}_{3}a^{2} = 0.3$ ,

$k_{3}/\hat{\mu}_{3} = 3$ .

DownLoad: Full-Size Img PowerPoint

Figure 6. Illustrations for

$K$ and

$\hat{K}$ towards the spacing ratio

$a/b$ for

$(a)$ a set of values of

$\mu_{32}$ with

$\mu_{12}\to\, 0$ ,

$s_{1} = s_{3} = 0.2$ ,

$\gamma_{2}/\mu_{2}a^{2} = 0.3$ ,

$k_{2}/\mu_{2} = 3$ ;

$(b)$ a set of values of

$\mu_{23}$ with

$\mu_{21}\to\infty$ ,

$s_{2} = 0.2$ ,

$\gamma_{3}/\hat{\mu}_{3}a^{2} = 0.3$ ,

$k_{3}/\hat{\mu}_{3} = 3$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. Illustrations for

$K$ and

$\hat{K}$ towards the spacing ratio

$a/b$ for

$(a)$ a set of values of

$k_{2}/\mu_{2}$ with

$\mu_{12} = \mu_{32} = 1$ ,

$s_{1} = s_{3} = 0.2$ ,

$\gamma_{2}/\mu_{2}a^{2} = 0.3$ ;

$(b)$ a set of values of

$k_{3}/\hat{\mu}_{3}$ with

$\mu_{21} = \mu_{23} = 1$ ,

$s_{2} = 0.2$ ,

$\gamma_{3}/\hat{\mu}_{3}a^{2} = 0.3$ .

DownLoad: Full-Size Img PowerPoint

Figure 8. Illustrations for

$K$ and

$\hat{K}$ towards the viscosity ratio for

$(a)$ a set of values of

$s_{1} = s_{3}$ and

$\mu_{12} = \mu_{32}$ with

$k_{2}/\mu_{2} = 4$ ,

$a/b = 0.3$ ,

$\gamma_{2}/\mu_{2}a^{2} = 0.4$ ;

$(b)$ a set of values of

$s_{2}$ and

$\mu_{21} = \mu_{23}$ with

$k_{3}/\hat{\mu}_{3} = 4$ ,

$a/b = 0.3$ ,

$\gamma_{3}/\hat{\mu}_{3}a^{2} = 0.4$ .

DownLoad: Full-Size Img PowerPoint

Table 1. Outcomes for

$K$ at a set of values of

$a/b$ with

$\mu_{32}\to\infty$ ,

$s_{1} = 0.2$ ,

$k_{2}/\mu_{2} = 1$ ,

$\gamma_{2}/\mu_{2}a^{2} = 0.4$ , and

$\mu_{12} = 0, 1, 10, \infty$ .

	$K$
$a/b$	$\mu_{12}\to\, 0$		$\mu_{12}=1$		$\mu_{12}=10$		$\mu_{12}\to\infty$
	Present	Salem^[30]	Present	Salem^[30]	Present	Salem^[30]	Present	Salem^[30]
0.1	1.18447	1.18447	1.23468	1.23468	1.30300	1.30300	1.32411	1.32411
0.2	1.45221	1.45221	1.59325	1.59325	1.81151	1.81151	1.88604	1.88604
0.3	1.86250	1.86250	2.15432	2.15432	2.68359	2.68359	2.88975	2.88975
0.4	2.55574	2.55574	3.08591	3.08591	4.24651	4.24651	4.77912	4.77911
0.5	3.91032	3.91032	4.81430	4.81430	7.29601	7.29601	8.68932	8.68930
0.6	7.09773	7.09773	8.58877	8.58877	14.0760	14.0760	18.0404	18.0403
0.7	16.7280	16.7280	19.0457	19.0457	32.4621	32.4621	45.9502	45.9499
0.8	60.3240	60.3240	62.2303	62.2303	102.765	102.765	168.377	168.376
0.9	547.814	547.814	501.854	501.854	701.264	701.265	1475.33	1475.30

| Show Table

DownLoad: CSV

Table 2. Outcomes for

$\hat{K}$ at a set of values of

$a/b$ with

$\mu_{23}\to\, 0$ and

$\mu_{21} = 0, 1, \infty$ .

	$\hat{K}$
$a/b$	$\mu_{21}\to\, 0$		$\mu_{21}=1$		$\mu_{21}\to\infty$
	Present	Happel et al.^[31]	Present	Happel et al.^[31]	Present	Happel et al.^[31]
0.1	1.28620	1.286	1.22888	1.229	1.17647	1.176
0.2	1.75585	1.756	1.57510	1.575	1.42841	1.428
0.3	2.57264	2.573	2.12613	2.126	1.81519	1.815
0.4	4.10593	4.106	3.06598	3.066	2.46888	2.469
0.5	7.29412	7.294	4.83019	4.831	3.72222	3.722
0.6	14.9481	14.948	8.63260	8.636	6.56909	6.569
0.7	37.8296	37.830	18.7886	18.762	14.8255	14.826
0.8	138.224	138.224	58.4112	58.480	50.7734	50.773
0.9	1209.78	1209.78	431.732	431.779	439.156	439.156

| Show Table

DownLoad: CSV

Table 3. Outcomes for

$K$ and

$\hat{K}$ at a set of values of

$a/b$ ,

$\mu_{32} = \mu_{23}$ ,

$\mu_{12}$ , and

$\mu_{21}$ ,

$(a)$ for

$K$ :

$\gamma_{2}/\mu_{2}a^{2} = 0.2$ ,

$k_{2}/\mu_{2} = 2$ ,

$s_{1} = s_{3} = 0.4$ ,

$(b)$ for

$\hat{K}$ :

$\gamma_{3}/\hat{\mu}_{3}a^{2} = 0.2$ ,

$k_{3}/\hat{\mu}_{3} = 2$ ,

$s_{2} = 0.4$ .

$\mu_{32}$	$a/b$	$K$				$\hat{K}$
$\mu_{32}$	$a/b$	$\mu_{12}\to\, 0$	$\mu_{12}=1$	$\mu_{12}=10$	$\mu_{12}\to\infty$	$\mu_{21}\to\, 0$	$\mu_{21}=1$	$\mu_{21}=10$	$\mu_{21}\to\infty$
	0.1	1.11201	1.13685	1.17884	1.19431	1.28577	1.22856	1.18540	1.17622
	0.2	1.25455	1.31967	1.43850	1.48531	1.75306	1.57312	1.45148	1.42700
	0.3	1.44206	1.57453	1.84119	1.95664	2.56170	2.11905	1.85914	1.81026
	0.4	1.69939	1.94873	2.51629	2.79630	4.06904	3.04431	2.54096	2.45372
0	0.5	2.07072	2.53193	3.74891	4.46693	7.17170	4.76522	3.82266	3.67514
	0.6	2.64006	3.51212	6.23121	8.26556	14.5085	8.42245	6.64776	6.40650
	0.7	3.59642	5.38026	12.0209	18.7975	35.9148	17.9648	14.4942	14.1264
	0.8	5.50334	9.95697	29.8887	61.0249	125.731	53.5540	46.4325	46.1493
	0.9	11.1900	30.5670	136.469	471.932	983.446	350.677	344.785	351.074
	0.1	1.13213	1.16164	1.21203	1.23074	1.24737	1.19877	1.16174	1.15382
	0.2	1.30472	1.38189	1.52582	1.58362	1.63073	1.48507	1.38402	1.36343
	0.3	1.53969	1.69360	2.01417	2.15714	2.25491	1.91471	1.70535	1.66508
	0.4	1.87738	2.15721	2.82438	3.16645	3.34003	2.59591	2.20199	2.13123
1	0.5	2.39852	2.89346	4.27839	5.13190	5.40209	3.76021	3.04099	2.92189
	0.6	3.28600	4.17634	7.16283	9.50012	9.85202	5.97492	4.64184	4.44183
	0.7	5.04405	6.77201	13.8252	21.3471	21.5522	10.9372	8.29146	7.94171
	0.8	9.60106	13.6793	34.2076	67.6437	65.3256	25.7096	19.4867	18.8006
	0.9	31.6019	48.2851	154.155	502.384	443.724	109.340	85.4741	83.5743
	0.1	1.17824	1.21913	1.29060	1.31767	1.17646	1.14285	1.11675	1.11111
	0.2	1.43800	1.55160	1.77613	1.87119	1.42803	1.33319	1.26436	1.25000
	0.3	1.84647	2.08233	2.62728	2.89527	1.81152	1.59845	1.45690	1.42857
	0.4	2.55785	2.99013	4.19894	4.91965	2.44813	1.98981	1.71845	1.66667
$\infty$	0.5	3.98137	4.71449	7.30363	9.26347	3.62963	2.61224	2.09385	2.00000
	0.6	7.41546	8.57373	14.1600	19.8348	6.18788	3.71140	2.67705	2.50000
	0.7	18.0880	19.6395	32.5154	51.5787	13.1672	5.98740	3.70241	3.33333
	0.8	67.5554	67.2145	102.278	191.107	41.4779	12.2070	5.95270	5.00000
	0.9	628.579	570.798	706.453	1682.30	324.560	44.2038	14.2982	10.0000

| Show Table

DownLoad: CSV

Table 4. Outcomes for

$K$ at a set of values of

$k_{2}/\mu_{2}$ ,

$\mu_{12} = \mu_{32}$ ,

$s_{1}$ , and

$s_{3}$ , with

$a/b = 0.4$ and

$\gamma_{2}/\mu_{2}a^{2} = 0.1$ .

		$K$
$k_{2}/\mu_{2}$	$\mu_{12}$	$s_{1}=0.2$			$s_{1}=0.6$			$s_{1}=1$
		$s_{3}=0.2$	$s_{3}=0.6$	$s_{3}=1$	$s_{3}=0.2$	$s_{3}=0.6$	$s_{3}=1$	$s_{3}=0.2$	$s_{3}=0.6$	$s_{3}=1$
	0	1.68130	1.68298	1.68465	1.67107	1.67276	1.67444	1.66111	1.66282	1.66450
	2	2.79924	2.79949	2.79974	2.79146	2.79170	2.79195	2.78379	2.78404	2.78428
0.1	4	3.22628	3.22627	3.22625	3.21999	3.21998	3.21996	3.21377	3.21375	3.21374
	20	3.91771	3.91762	3.91753	3.91543	3.91534	3.91525	3.91316	3.91307	3.91298
	40	4.05135	4.05129	4.05124	4.05010	4.05004	4.04998	4.04884	4.04878	4.04873
	0	1.70548	1.70907	1.71259	1.67075	1.67434	1.67785	1.63889	1.64247	1.64597
	2	2.71871	2.71883	2.71894	2.68362	2.68373	2.68383	2.65037	2.65046	2.65055
0.7	4	3.19680	3.19605	3.19530	3.16556	3.16481	3.16406	3.13548	3.13473	3.13399
	20	4.12314	4.12233	4.12152	4.10947	4.10867	4.10786	4.09596	4.09516	4.09436
	40	4.32915	4.32864	4.32813	4.32130	4.32079	4.32028	4.31349	4.31299	4.31248
	0	1.70684	1.66754	1.63199	1.71024	1.67089	1.63531	1.71356	1.67417	1.63854
	2	2.37816	2.33346	2.29208	2.37864	2.33393	2.29253	2.37913	2.33439	2.29297
3	4	2.80033	2.75546	2.71325	2.79954	2.75468	2.71248	2.79875	2.75390	2.71171
	20	3.94777	3.91953	3.89194	3.94598	3.91776	3.89019	3.94420	3.91600	3.88845
	40	4.29268	4.27463	4.25683	4.29138	4.27334	4.25555	4.29008	4.27206	4.25427

| Show Table

DownLoad: CSV

Table 5. Some values of

$\hat{K}$ for different values of

$k_{3}/\hat{\mu}_{3}$ ,

$\mu_{21} = \mu_{23}$ , and

$s_{2}$ , with

$a/b = 0.4$ and

$\gamma_{3}/\hat{\mu}_{3}a^{2} = 0.1$ .

$k_{3}/\hat{\mu}_{3}$	$\mu_{21}$	$\hat{K}$
$k_{3}/\hat{\mu}_{3}$	$\mu_{21}$	$s_{2}=0.2$	$s_{2}=0.6$	$s_{2}=1$
	0	4.10015	4.08875	4.07756
	2	2.12047	2.12058	2.12068
0.1	4	1.91882	1.91901	1.91920
	20	1.72224	1.72231	1.72238
	40	1.69483	1.69486	1.69490
	0	4.09341	4.06912	4.04582
	2	2.17043	2.17040	2.17038
0.7	4	1.95073	1.95112	1.95151
	20	1.73029	1.73048	1.73066
	40	1.69898	1.69908	1.69919
	0	4.09287	4.06758	4.04336
	2	2.30880	2.30750	2.30622
3	4	2.04996	2.05003	2.05009
	20	1.75916	1.75946	1.75976
	40	1.71423	1.71441	1.71460

| Show Table

DownLoad: CSV

Figures 2 and 4 indicate the difference between the viscosity ratios in the two problems. Also, we test the accuracy of our results in some special cases by comparing them with the solutions of Salem ^[30] and Happel et al. ^[31]; see Tables 1 and 2, respectively. We can also use the CFD (Computional Fluid Dynamics) method (VOF model) to solve this problem and compare it with our analytical results.

Figures 5(a), (b) and , show that the results for the interface correction factors exerted on a solid sphere and a gas sphere bubble, respectively, moving inside a spherical interface between micropolar/viscous fluids against the spacing ratio $a/b$ at some values of $\mu_{32}$ and $\mu_{23}$ . and indicate the motion of a solid sphere $(\mu_{12}\to\infty)$ and a gas bubble $(\mu_{12}\to\, 0)$ , respectively, moving inside a micropolar fluid in the presence of a cavity wall $(\mu_{32}\to\infty)$ , coalescence $(\mu_{32} = 1)$ , and gas/liquid interface (free surface) $(\mu_{32}\to\, 0)$ , while and indicate the motion of a solid sphere $(\mu_{21}\to\, 0)$ and a gas bubble $(\mu_{21}\to\infty)$ , respectively, moving inside a viscous fluid with a cavity wall present $(\mu_{23}\to\, 0)$ , coalescence $(\mu_{23} = 1)$ , and gas/liquid interface (free surface) $(\mu_{23}\to\infty)$ . Figures 5(a), (b) and , indicate that $K$ and $\hat{K}$ increase monotonically with an increase in the spacing ratio $a/b$ and will grow into infinity when $a/b\to\, 1$ for any certain value of the remaining parameters. For a fixed value of $a/b$ and keeping the other parameters fixed, and show that $K$ increases with the increase of the viscosity ratio $\mu_{32}$ , while and show that $\hat{K}$ increases with a decrease in the viscosity coefficient $\mu_{23}$ , with the minimum and maximum impacts when there is an atmospheric air interface and a solid wall, respectively; this is also shown in Table 3. Clearly, in the case of a solid or gas sphere, the effect of the outer-on-inner interface in the case of a cavity wall is larger than in the case of atmospheric air. Additionally, the values of the drag forces are getting closer to agreement in the case of a solid sphere; while they are getting closer and closer to agreement in the case of a gas sphere, when moving from cavity to air case. Moreover, the drag force on a viscous droplet when it is immersed in micropolar fluid is greater than when it is immersed in viscous fluid; with the minimum and maximum effects in the cases of free atmospheric air interface and solid wall, respectively. Also, these forces depend on both the properties of the object and the properties of the fluid. Its also shown that the values of the drag force on a viscous droplet immersed in a viscous fluid are the largest when compared with those in a micropolar fluid.

, shows that the results for the interface correction factors $K$ and $\hat{K}$ exerted on a viscous sphere droplet moving inside a spherical interface between micropolar/viscous fluids against the spacing ratio $a/b$ at some values of $k_{2}/\mu_{2}$ and $k_{3}/\hat{\mu}_{3}$ . Both indicate that $K$ and $\hat{K}$ increase monotonously with the increase of the spacing coefficient $a/b$ . Also, in the case of $\mu_{12} = \mu_{32} = \mu_{21} = \mu_{23} = 1$ , for a fixed value of $a/b$ , $K$ increases with a decrease in the micropolarity parameter $k_{2}/\mu_{2}$ , while $\hat{K}$ increases with an increase in the micropolarity parameter $k_{3}/\hat{\mu}_{3}$ , holding constant the other parameters.

, shows the factors $K$ and $\hat{K}$ against the ratios $\mu_{32}$ and $\mu_{23}$ , respectively, for various coefficients. In regard to the complete range of spin parameters $s_{1}$ and $s_{2}$ , shows that $K$ monotonously increases as $\mu_{32}$ increases; while shows that $\hat{K}$ monotonously decreases as $\mu_{23}$ increases, holding constant the other parameters. Also, plots demonstrate that, for a fixed value of $\mu_{32}$ and $\mu_{23}$ , $K$ and $\hat{K}$ increase with a decrease in the spin parameters $s_{1}$ and $s_{2}$ , respectively. In addition, for a given value of $k_{2}/\mu_{2}$ and $\mu_{12}$ , shows that $K$ increases as $s_{3}$ increases keeping $s_{1}$ unchanged, while $K$ decreases as $s_{1}$ increases keeping $s_{3}$ unchanged; on the other hand, $K$ increases as $k_{2}/\mu_{2}$ increases keeping $s_{1}$ and $s_{3}$ unchanged. Moreover, shows that $\hat{K}$ increases as $k_{3}/\hat{\mu}_{3}$ increases; on the other hand, for a given value of $k_{3}/\hat{\mu}_{3}$ and $\mu_{12}$ , $\hat{K}$ decreases as $s_{1}$ increases to a predetermined value of $\mu_{12}$ (said $\mu_{o}$ ), hence it increases with an increase in $s_{2}$ for $\mu_{12} > \mu_{o}$ . To illustrate, in , if $k_{3}/\hat{\mu}_{3} = 3$ , $\hat{K}$ decreases with an increase in $s_{2}$ (from $0$ to $3$ ) up to $\mu_{o} = 4$ , hence it increases with an increase in $s_{2}$ . As expected, and show that when the micro-elements of the micropolar fluid surrounding the viscous droplet are in perfect spin $(s_{1} = s_{3} = 1)$ , $K$ has minimum, while for no spin $(s_{1} = s_{3} = 0)$ , it has maximum, while and show that when the micro-elements of the viscous fluid surrounding the viscous droplet are in perfect spin $(s_{2} = 1)$ , $\hat{K}$ has minimum, while for no spin $(s_{2} = 0)$ , it has a maximum. Clearly, for large/small values of viscosity ratios, the drag force is irrelevant with respect to the spin parameter.

6. Conclusions

A creeping axisymmetric translational movement of a spherical viscous drop moving at a concentric instantaneous position inside a spherical micropolar-viscous interface separating finite and semi-infinite immiscible fluid phases is studied. A connected issue is also studied when a viscous-micropolar interface is present and the viscous sphere droplet is embedded in a viscous fluid. We dealt with three immiscible fluid phases in three different regions. Analytical solutions are obtained for the viscous and micropolar equations pertaining to the fluid flow field associated with these movements, and the effect of interaction between the viscous droplet and the fluid-fluid interface is stated by obtaining formulaes for the interface correction factors. Many special cases are obtained from this study, for example, the movement of a solid sphere and a gas bubble moving inside a micropolar or viscous fluid in the presence of a cavity, coalescence, and gas/liquid interface. As found, the normalised hydrodynamic drag force in general applying on the viscous droplet's surface increases as a function of the droplet-to-interface radius ratio; on the other hand, it is a decreasing and increasing function of the micropolarity parameters, the relative viscosity of the fluid-fluid interface, and the spin parameters. As found, the viscous sphere droplet encounters a maximum interface correction factor when the fluid-fluid interface is to be a cavity wall and a minimum when the fluid-fluid interface is to be a gas/liquid interface. In the two cases of a cavity wall and a gas/liquid interface, as found, the viscous sphere droplet encounters a maximum interface correction factor when the viscous sphere droplet is to be a solid sphere and a minimum when the viscous sphere droplet is to be a gas bubble. Also, at the fluid-fluid interface, as found, the interface correction factors are significantly influenced by the spin parameters. Our results for special cases are in good agreement with the solutions obtained by Salem ^[30] and Happel et al. ^[31].

Author contributions

Ahmed G. Salem: Supervision, conceptualization, software, writing-original draft, writing–review and editing; Turki D. Alharbi: Writing–review and editing; Abdulaziz H. Alharbi: Supervision, writing–review and editing; Anwar Ali Aldhafeeri: Funding acquisition, writing–review and editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Grant No. KFU241994].

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

[1]	E. D. Sontag, Smooth stabilization implies coprime factorization, IEEE Trans. Automat. Control, 34 (1989), 435–443. https://doi.org/10.1109/9.28018 doi: 10.1109/9.28018
[2]	E. D. Sontag, Y. Wang, On characterizations of the input-to-state stability property, Syst. Control Lett., 24 (1995), 351–359. https://doi.org/10.1016/0167-6911(94)00050-6 doi: 10.1016/0167-6911(94)00050-6
[3]	E. D. Sontag, Y. Wang, New characterizations of input-to-state stability, IEEE Trans. Automat. Control, 41 (1996), 1283–1294. https://doi.org/10.1109/9.536498 doi: 10.1109/9.536498
[4]	M. Vidyasagar, Input-output analysis of large-scale interconnected systems, In: Lecture notes in control and information sciences, Heidelberg: Springer Berlin, 29 (1981). https://doi.org/10.1007/BFb0044060
[5]	R. Geiselhart, M. Lazar, F. R. Wirth, A relaxed small-gain theorem for interconnected discrete-time systems, IEEE Trans. Automat. Control, 60 (2015), 812–817. https://doi.org/10.1109/TAC.2014.2332691 doi: 10.1109/TAC.2014.2332691
[6]	Z.-P. Jiang, Y. Wang, Input-to-state stability for discrete-time nonlinear systems, Automatica, 37 (2001), 857–869. https://doi.org/10.1016/S0005-1098(01)00028-0 doi: 10.1016/S0005-1098(01)00028-0
[7]	R. Geiselhart, F. R. Wirth, Relaxed ISS small-gain theorems for discrete-time systems, SIAM J. Control Optim., 54 (2016), 423–449. http://doi.org/10.1137/14097286X doi: 10.1137/14097286X
[8]	H. Lin, P. J. Antsaklis, Stability and stabilizability of switched linear systems: A survey of recent results, IEEE Trans. Automat. Control, 54 (2009), 308–322. https://doi.org/10.1109/TAC.2008.2012009 doi: 10.1109/TAC.2008.2012009
[9]	J. Lu, Z. She, S. S. Ge, X. Jiang, Stability analysis of discrete-time switched systems via multi-step multiple Lyapunov-like functions, Nonlinear Anal. Hybrid Syst., 27 (2018), 44–61. https://doi.org/10.1016/j.nahs.2017.07.004 doi: 10.1016/j.nahs.2017.07.004
[10]	Q. Yu, H. Lv, Stability analysis for discrete-time switched systems with stable and unstable modes based on a weighted average dwell time approach, Nonlinear Anal. Hybrid Syst., 38 (2020), 100949. https://doi.org/10.1016/j.nahs.2020.100949 doi: 10.1016/j.nahs.2020.100949
[11]	J. Lu, Z. She, B. Liu, S. S. Ge, Analysis and verification of input-to-state stability for nonautonomous discrete-time switched systems via semidefinite programming, IEEE Trans. Automat. Control, 66 (2021), 4452–4459. https://doi.org/10.1109/TAC.2020.3046699 doi: 10.1109/TAC.2020.3046699
[12]	L. Vu, D. Chatterjee, D. Liberzon, Input-to-state stability of switched systems and switching adaptive control, Automatica, 43 (2007), 639–646. https://doi.org/10.1016/j.automatica.2006.10.007 doi: 10.1016/j.automatica.2006.10.007
[13]	W. Xie, C. Wen, Z. Li, Input-to-state stabilization of switched nonlinear systems, IEEE Trans. Automat. Control, 46 (2001), 1111–1116. https://doi.org/10.1109/9.935066 doi: 10.1109/9.935066
[14]	G. Yang, D. Liberzon, Input-to-state stability for switched systems with unstable subsystems: A hybrid Lyapunov construction, In: 53rd IEEE conference on decision and control, 2014. https://doi.org/10.1109/CDC.2014.7040367
[15]	M. Sharifi, N. Noroozi, R. Findeisen, Lyapunov characterizations of input-to-state stability for discrete-time switched systems via finite-step lyapunov functions, IFAC-PapersOnLine, 53 (2020), 2016–2021. https://doi.org/10.1016/j.ifacol.2020.12.2510 doi: 10.1016/j.ifacol.2020.12.2510
[16]	S. Liu, A. Tanwani, D. Liberzon, ISS and integral-ISS of switched systems with nonlinear supply functions, Math. Control Signals Syst., 34 (2022), 297–327.
[17]	H. Li, A. Liu, Asymptotic stability analysis via indefinite Lyapunov functions and design of nonlinear impulsive control systems, Nonlinear Anal. Hybrid Syst., 38 (2020), 100936. https://doi.org/10.1016/j.nahs.2020.100936 doi: 10.1016/j.nahs.2020.100936
[18]	P. Zhao, Y. Kang, B. Niu, Y. Zhao, Input-to-state stability and stabilization for switched nonlinear positive systems, Nonlinear Anal. Hybrid Syst., 47 (2023), 101298. https://doi.org/10.1016/j.nahs.2022.101298 doi: 10.1016/j.nahs.2022.101298
[19]	B. Liu, M. Yang, T. Liu, D. J. Hill, Stabilization to exponential input-to-state stability via aperiodic intermittent control, IEEE Trans. Automat. Control, 66 (2021), 2913–2919. https://doi.org/10.1109/TAC.2020.3014637 doi: 10.1109/TAC.2020.3014637
[20]	W. Wang, R. Postoyan, D. Nešić, W. P. M. H. Heemels, Periodic event-triggered control for nonlinear networked control systems, IEEE Trans. Automat. Control, 65 (2020), 620–635. https://doi.org/10.1109/TAC.2019.2914255 doi: 10.1109/TAC.2019.2914255
[21]	Y. Guo, M. Duan, P. Wang, Input-to-state stabilization of semilinear systems via aperiodically intermittent event-triggered control, IEEE Trans. Control Netw. Syst., 9 (2022), 731–741. https://doi.org/10.1109/TCNS.2022.3165511 doi: 10.1109/TCNS.2022.3165511
[22]	D. S. Xu, X. J. He, H. Su, Dynamic periodic event-triggered control for input-to-state stability of multilayer coupled systems, Internat. J. Control, 2022. https://doi.org/10.1080/00207179.2022.2152380 doi: 10.1080/00207179.2022.2152380
[23]	S. Chen, C. Ning, Q. Liu, Q. Liu, Improved multiple Lyapunov functions of input–output-to-state stability for nonlinear switched systems, Inform. Sci., 608 (2022), 47–62. https://doi.org/10.1016/j.ins.2022.06.025 doi: 10.1016/j.ins.2022.06.025
[24]	X. Wu, Y. Tang, J. Cao, Input-to-state stability of time-varying switched systems with time delays, IEEE Trans. Automat. Control, 64 (2019), 2537–2544. https://doi.org/10.1109/TAC.2018.2867158 doi: 10.1109/TAC.2018.2867158
[25]	L. Zhou, H. Ding, X. Xiao, Input-to-state stability of discrete-time switched nonlinear systems with generalized switching signals, Appl. Math. Comput., 392 (2021), 125727. https://doi.org/10.1016/j.amc.2020.125727 doi: 10.1016/j.amc.2020.125727
[26]	H. Li, A. Liu, L. Zhang, Input-to-state stability of time-varying nonlinear discrete-time systems via indefinite difference Lyapunov functions, ISA Trans., 77 (2018), 71–76. https://doi.org/10.1016/j.isatra.2018.03.022 doi: 10.1016/j.isatra.2018.03.022
[27]	H. Li, Stability analysis of time-varying switched systems via indefinite difference Lyapunov functions, Nonlinear Anal. Hybrid Syst., 48 (2023), 101329. https://doi.org/10.1016/j.nahs.2022.101329 doi: 10.1016/j.nahs.2022.101329
[28]	M. A. Müller, D. Liberzon, Input/output-to-state stability and state-norm estimators for switched nonlinear systems, Automatica, 48 (2012), 2029–2039. https://doi.org/10.1016/j.automatica.2012.06.026 doi: 10.1016/j.automatica.2012.06.026

This article has been cited by:

1.	Ahmed G Salem, Influence of interface on nondeformable micropolar drop migration, 2024, 56, 0169-5983, 065502, 10.1088/1873-7005/ad8b66
2.	Ahmed G. Salem, Migration of a slip-spin solid spherical particle in a micropolar fluid-filled circular cylindrical tube, 2024, 92, 05779073, 1144, 10.1016/j.cjph.2024.10.024
3.	Ahmed G. Salem, Flow of a micropolar drop in an impermeable micropolar circular pipe, 2025, 95, 0939-1533, 10.1007/s00419-024-02738-8

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)