Efficient control chart-based monitoring of scale parameter for a process with heavy-tailed non-normal distribution

1.   Introduction

Researchers have recently placed a great deal of emphasis on investigating the propagation of soliton solutions in nonlinear systems (NSs) of FNPDEs. In engineering and applied sciences, such solutions are required to describe nonlinearity. Many NSs have been utilized to explain phenomena in physics, for example, heat flow, chemical kinematics, electricity, wave propagation, shallow water waves, fluid mechanics, plasma physics, optical fibers, and quantum mechanics ^{[1,2,3,4,5,6,7]}. FNPDEs also appear in the literature in various applications such as chemistry, population modeling, ecology, geochemistry, chemical reactivity of materials, and several others. Obtaining exact and numerical solutions to NSs is an essential and significant task that is becoming increasingly important in understanding physical phenomena ^{[8,9,10,11,12,13]}. On the other hand, accurate soliton solutions give us a deeper understand of some physical phenomena than numerical solutions from the viewpoint of NSs. Thus, investigating the exact soliton solutions of NSs is a critical issue for these physical phenomena. So far, for these NSs, many numerical and analytical techniques have been used to extract exact soliton solutions in many types. In 2024, Meng et al. introduced a method for designing observers for nonlinear generalized systems with nonlinear algebraic constraints, contributing to advancements in control system design ^[14]. Additionally, Cai et al. (2021) explored the dynamic control of terahertz wavefronts using cascaded metasurfaces, providing insights into photonics and wave engineering ^[15]. Guo et al. (2023) presented innovative approaches for fixed-time tracking control of uncertain nonlinear pure-feedback systems, contributing to robust control methodologies ^[16,17]. Furthermore, Kai et al. (2022) and Zhou et al. (2023) focused on nonlinear dynamics and signal processing, respectively, exploring topics such as the generalization of regularized long-wave equations and an iterative threshold algorithm for sparse problems ^[18,19,20]. These include the auxiliary equation method ^[21], generalized extended rational expansion method ^[22], (G'/G)-expansion method ^[23], Fan sub-equation method ^[24], homotopy asymptotic method ^[25], Hirota bilinear method ^[26], homotopy perturbation method ^[27], Darboux transformation ^[28], Bücklund transformation method ^[29], Painlevé expansion method ^[30], extended tanh method ^[31], elliptic function method ^[32], the mapping method ^[33], EDAM ^[34,35,36], and many others ^{[37,38,39,40,41]}.

The (2+1)-dimensional Broer-Kaup-Kupershmidt system (BKKS) ^[42,43] is a set of partial differential equations (PDEs) that are generated from the Kadomtsev-Petviashvili (KP) equation ^[44] through an extension of inner parameter-dependent symmetry constraints, and present themselves as models for nonlinear and dispersive long waves, for fields in two horizontal directions within shallow water of constant depth. This is the driving force behind the current study, which focuses on soliton dynamics in the context of the CBKKS. This model is a fractional generalization of BKKS, replacing traditional integer-order derivatives with conformable derivatives. This model is articulated as follows:

where $0 < \rho, \varrho, \sigma\leq1$, $w\equiv w(x, y, t)$, $z\equiv z(x, y, t)$ and the derivative operators $D_{x}^{\rho}(\cdot)$, $D_{y}^{\varrho}(\cdot),$ and $D_{t}^{\sigma}(\cdot)$ represent spatial and time conformable derivatives. Notably, the BBKS reduces to the Whitham-Broer-Kaup System (WBKS) for $y = x$ and $\rho = \varrho = \sigma = 1$, which describes dispersive long waves in shallow water ^[45,46,47] and was constructed using the Boussinesq approximation, and was characterized by parameters reflecting different diffusion powers. A comprehensive understanding of the solutions to the NSs above proves immensely beneficial for engineers and coastal experts, enabling them to solve nonlinear water wave models across varied scientific and engineering areas. As a result, the search for different kinds of traveling wave solutions for these coupled systems continues to be an essential field in fluid dynamics, with many articles devoted to discovering exact and numerical solutions for these equations.

In this research, we expand the EDAM to get soliton solutions to the fractional CBKKS (1.1). The proposed EDAM primarily reduces the CBKKS to a system of integer-ordered NODEs under the traveling wave transformation, yielding an algebraic system of equations. The ensuing algebraic problem systems are then solved to construct the soliton solutions, particularly rogue and breather soliton solutions. A soliton is a localized, stable wave solution that travels through a nonlinear medium without changing its form or speed. A breather is a particular kind of soliton with regular amplitude oscillations. These oscillations indicate little areas of the wave that are compressed and expanded. An exceptionally big and isolated soliton, known as a rogue soliton, can arise unexpectedly in a medium and is frequently connected to severe and infrequent events in nonlinear systems.

This article is structured as follows: An introduction is given in Section 1. The definition of conformable derivative and methodology are presented in Section 2. We construct some new soliton solutions for CBKKS in Section 3, while Section 4 presents some depictions and a graphical discussion. Lastly, the conclusion is given in Section 5.

2.   Method & materials

2.1.   Conformable derivative

The FNPDEs can be solved explicitly by utilizing the unique benefits of conformable fractional derivatives over other fractional derivative operators. Surprisingly, different ways of looking at the fractional derivative for Eq (1.1) do not give traveling wave solutions and solitons because they break the chain rule ^[48,49]. Equation (1.1) was, therefore, changed to incorporate conformable fractional derivatives ^[50] gives the following definition for the conformable fractional derivative operator of order $\varrho$:

In this investigation, we make use of the following properties of the fractional derivatives:

where $\rho(\upsilon)$, $\eta(\upsilon)$, $\chi(\upsilon),$ and $\zeta (\upsilon)$ are arbitrary differentiable functions, whereas $b$, $b_{1},$ and $b_{2}$ signify constants.

2.2.   The operational procedure of EDAM

In this part, we outline the operating strategy of the EDAM by considering the FNPDE:

where $z = z(t, x_{1}, x_{2}, x_{3}, \ldots, x_{r})$. The steps listed below are utilized for solving Eq (2.5):

(I) We begin with a variable transformation of the type $z(t, x_{1}, x_{2}, x_{3}, \dots, x_{r}) = Z(\upsilon)$, where $\upsilon$ can be written in several ways. Then, Eq (2.5) is transformed into the subsequent NODE

where $Z^{\prime} = \frac{dZ}{d\upsilon}$. Occasionally, the NODE can be made suitable for the homogeneous balancing principle by integrating Eq (2.6).

(II) Next, we suppose the following series-based solution to the NODE in Eq (2.6) using the Riccati ODE:

In this context, $A_{k}(k = -\gamma, ..., \gamma)$ denotes the unknown constants, and $\Upsilon(\upsilon)$ is the general solution of the resulting ODE:

where $P, Q,$ and $R$ are constants.

(III) The positive integer $\gamma$ appearing in Eq (2.8) can be obtained by making an even balance in Eq (2.6) between the largest nonlinearity and the highest-order derivative. Using the following mathematical formulas, we can determine the balance number $\gamma$ with greater accuracy:

where $D$ expresses degree of $U(\upsilon)$, whereas $k, n,$ and $m$ are positive integers.

(IV) Following that, we place Eq (2.7) into Eq (2.6) or the equation that results from the integration of Eq (2.6) and bring together the terms of $\Upsilon(\upsilon)$ into similar orders. An expression in the terms of $\Upsilon(\upsilon)$ is obtained by using this procedure. The variables $A_{k}(k = -\gamma, ..., \gamma)$ and other related parameters are then represented by an algebraic system of equations when the coefficients in this expression are set to zero.

(V) This system of nonlinear algebraic equations can be solved using Maple or Wolfram Mathematica.

(VI) After that, by calculating and inserting the unknown values into Eq (2.7), together with the $\Upsilon(\upsilon)$ (the solution of Eq (2.7)), analytical soliton solutions for Eq (2.5) can be obtained. We can generate the ensuing families of soliton solutions by employing the general solution of Eq (2.8).

Family 1: For $\Lambda < 0$ and $R\neq0$, we get

Family 2: For $\Lambda > 0$ and $R\neq0$, we get

Family 3: For $QP > 0$ and $Q = 0$, we get

Family 4: For $PR < 0$ and $Q = 0$, we get

Family 5: For $P = R$ & $Q = 0$, we get

Family 6: For $R = -P$ and $Q = 0$, we get

Family 7: For $\Lambda = 0$, we get

Family 8: For $Q = \tau$, $P = h\tau(h\neq0)$ and $R = 0$, we get

Family 9: For $Q = R = 0$, we get

Family 10: For $Q = P = 0$, we get

Family 11: For $P = 0$, $Q\neq0$ and $R\neq0$, we get

Family 12: For $Q = \tau$, $R = h\tau(h\neq0)$ and $P = 0$, we get

where $\Lambda = Q^{2}-4RP$.

3.   Execution of EDAM to CBKKS

This section uses the EDAM technique to develop soliton solutions for the CBKKS, as indicated in Eq (1.1). For this purpose, first, the following variable transformation must be performed in order to initiate the method:

Applying this transformation to Eq (1.1) yields the following system of NODEs:

The following outcome is obtained by integrating the first equation in system (3.2) three times with a zero integration constant:

Substituting the above result in the second equation of system (3.2) yields the following NODE:

where $K$ is the constant of integration. After using the formula given in step (III) of Section. 2, for establishing a homogeneous balancing condition between $W^{3}$ and $W^{\prime\prime}$, we get $\gamma+2 = 3\gamma$ which implies $\gamma = 1$. By replacing $\gamma = 1$ in Eq (2.7), we get the following series-based solution for Eq (3.4):

Inserting Eq (3.5) into Eq (3.4) and collecting terms with the same powers of $\Upsilon(\upsilon)$, we get an expression in $\Upsilon(\upsilon)$. The process yields a set of algebraic nonlinear equations when the coefficients are set to zero. The two sets of solutions offered when using Maple to solve this system are as follows:

Case 1:

Case 2:

For Case 1, and by using Eqs (3.1), (3.3), and (3.5) and the corresponding general solution of Eq (2.8), we construct the families of soliton solutions for CBKKS (1.1) as follows:

Family 1.1: For $\Lambda < 0$ and $R\neq0$, we get

and

Family 1.2: For $\Lambda > 0$ and $R\neq0$, we get

and

Family 1.3: For $PR > 0$ and $Q = 0$,

and

Family 1.4: For $PR > 0$ and $Q = 0$, we get

and

Family 1.5: For $R = P$ and $Q = 0$, we get

and

Family 1.6: For $R = -P$ and $Q = 0$, we get

and

Family 1.7: For $Q = \tau$, $P = h\tau(h\neq0)$, and $R = 0$, we get

where $\upsilon = \frac{\alpha x^\rho}{\rho}+\frac{(-{\frac {36}{5}}\, {\frac {K}{{ \alpha}^{5}\sqrt {-6\, \Lambda}\Lambda}}) y^\varrho}{\varrho}+\frac{(-\frac{1}{2}\, {\alpha}^{2} \sqrt {-6\, \Lambda}) t^\sigma}{\sigma}$.

For Case 1, and by using Eqs (3.1), (3.3), and (3.5) and the corresponding general solution of Eq (2.8), we construct the following families of soliton solutions for CBKKS Eq (1.1):

Family 2.1: For $\Lambda < 0$ and $\quad R\neq0$, we get

and

Family 2.2: When $\Lambda > 0$ and $\quad R\neq0$,

and

Family 2.3: For $PR > 0$ and $Q = 0$, we get

and

Family 2.4: For $PR > 0$ and $Q = 0$, we get

and

Family 2.5: For $R = P$ and $Q = 0$, we get

and

Family 2.6: For $R = -P$ and $Q = 0$, we get

and

Family 2.7: For $P = 0$, $R\neq0$ and $Q\neq0$, we get

and

Family 2.8: For $Q = \tau$, $R = h\tau(h\neq0)$ and $P = 0$, we get

where $\upsilon$ has the same value as given above.

4.   Discussion and graphs

This section contains graphic representations of various waveforms contained in the examined models. The findings show that EDAM stands out for having various solutions derived using this technology. The wave structures consist of periodic waves, breathers, rogue soliton solutions, and several other traveling wave solutions expressed in trigonometric or hyperbolic functions. Carefully chosen parameters produce distinctive and informative visuals. Furthermore, this research's findings are novel since this method's outcomes have never been applied to the (2+1)-dimensional CBKKS in the literature.

A soliton is a special kind of self-reinforcing solitary wave that emerges in nonlinear and dispersive situations and retains its shape and velocity while moving across a medium. This study identified two solitons: breather solitons, which display localized periodic oscillations, and rogue solitons, which have abnormally big and isolated waves. Breather solitons result from the interaction between dispersion and nonlinearity in media, where dispersive effects prevent spreading, but nonlinear factors lead to self-focusing. In the same way, nonlinearity and dispersion work together to make rogue solitons. Nonlinear effects focus energy, while dispersive factors change how they are made and how stable they are. The study uses the Boussinesq approximation to focus on long gravity waves in shallow water. Parameters representing various diffusion powers emphasize the interaction between nonlinear and dispersive properties in producing breathers and rogue solitons, advancing our knowledge of intricate wave dynamics.

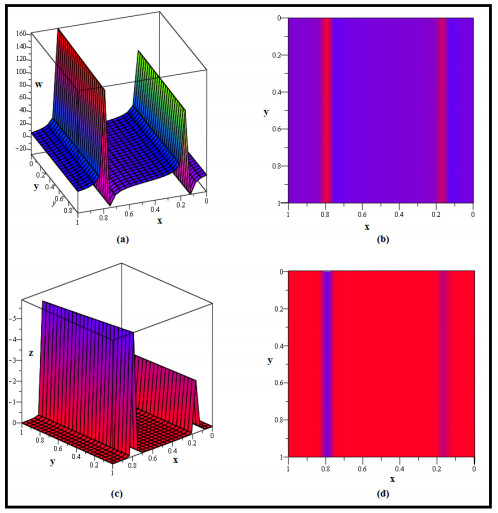
Using some appropriate values for the parameters related to the derived solutions that satisfy the conditions and constraints on these solutions, some derived solutions are analyzed numerically, as shown in Figures 1–11. For example, we analyzed solutions (3.8) and (3.27), as shown in Figures 1 and 2, respectively, utilizing specific values for the solution parameters to meet the requirements of these solutions. These figures illustrate that the first part of these solutions represents a periodic wave, while the second part represents a breather soliton. Figure 1(a) indicates 3D graphics, while Figure 1(b) indicates contour graphics for the first part of the solution (3.8). On the other side, Figure 1(c) shows 3D graphics, while Figure 1(d) shows contour graphics for the second part of the solution (3.8). In the same way, Figures 2(a)–2(d) can be classified. It is essential to mention that upon analyzing the majority of the numerically derived solutions, it was evident that they yielded nearly identical results to these solutions. To avoid redundancy, we illustrated only the figures for solutions (3.8) and (3.27) to represent the other types of solutions. The real and imaginary parts of the rogue wave-like (RW-like) solution (3.38) are analyzed numerically, as shown in Figures 3(a) and 3(b), respectively. Moreover, the impact of the space and time fractional parameters $\left(\rho, \varrho, \sigma\right)$ on the profile of the RW-like solution (3.38) is examined as illustrated in Figures 4(a)–4(f).

Moreover, soliton solutions (3.64) of case II are graphically analyzed as illustrated in Figure 5, which Figure 5(a) indicates the first part of the solution (3.64) $\left\vert w_{2, 26}\right\vert$ whereas Figure 5(b) refers to the second part of the solution (3.64) $\left\vert z_{2, 26}\right\vert$. We also studied the effect of the fractional parameter $\rho$ on the soliton profile, as shown in Figures 6(a) and 6(b) for $\left\vert w_{2, 26}\right\vert$ and $\left\vert z_{2, 26}\right\vert$, respectively. In addition, we analyzed soliton solutions (3.66) for both $\left\vert w_{2, 28}\right\vert$ and $\left\vert z_{2, 28}\right\vert$, as is clear in Figures 7(a) and 7(b), respectively. Furthermore, solutions (3.69) are examined as demonstrated in Figures 8(a) and 8(b) for $\left\vert w_{2, 31}\right\vert$ and $\left\vert z_{2, 31}\right\vert$, respectively. Also, the impact of the fractional parameter $\rho$ on the profiles of solutions (3.69) is investigated as elucidated in Figures 9(a) and 9(b) for $\left\vert w_{2, 31}\right\vert$ and $\left\vert z_{2, 31}\right\vert$, respectively. In addition, we visually examined several more derived soliton solutions (we mean here solutions (3.71)), as depicted in Figures 10(a) and 10(b) for $\left\vert w_{2, 38}\right\vert$ and $\left\vert z_{2, 38}\right\vert$, respectively. We also discussed the impact of different fractional parameters $\left(\rho, \varrho, \sigma\right)$ on the solitons profiles as depicted in Figures 11(a)–11(f).

5.   Conclusions

To sum up, the Extended Direct Algebraic Method (EDAM) was applied to anatomy and solve the space-time fractional (2+1)-dimensional Conformable Broer-Kaup-Kupershmit System (CBKKS). For this purpose, a suitable traveling wave transformation was used to reduce the space-time fractional partial differential (2+1)-dimensional CBKKS to an integer-order nonlinear ordinary differential equation (NODE), resulting in an algebraic system of equations. Subsequently, the solutions to these algebraic systems were employed to construct different types of traveling wave solutions and soliton-like solutions. Accordingly, two different cases were produced under specific parameters for each case. By analyzing each case separately, several distinct families of solutions were derived. In this investigation, Maple was employed to analyze and solve the present issue by employing the EDAM, thereby deriving several forms of traveling wave solutions. The derived solutions were graphically and numerically explored using Wolfram Mathematica to gain a comprehensive understanding of their nature and dynamics. We also studied the effect of different fractional parameters on the profile of some derived solutions to understand the extent of their influence on the shape of the waves and to capture some information that was not known before, as is the case in non-fractional cases. The soliton solutions found have implications for fluid mechanics since they shed light on the nonlinear behavior of the CBKKS model and open up new avenues for our comprehension of intricate physical processes.

Future work: The stochastic components can be considered in the current problem of the study as a direction for future research to examine the model's behavior under random influences, thereby deepening our comprehension of its dynamics and possible uses in stochastic systems. Moreover, the present methodology distinguishes itself by its abundance of derived solutions. Hence, it can examine various evolution equations encompassing intricate physical and engineering phenomena. Numerous nonlinear solutions can be constructed for various wave equations describing nonlinear processes in diverse plasma systems. These equations include the KdV-type equations ^[51,52,53], the Kawahara-type equations ^[54,55,56], the nonlinear Schrodinger-type equations ^[57,58,59], and other fractional forms.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence tools in the creation of this article.

Funding

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2024R378), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 6152).

Acknowledgments

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2024R378), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 6152).

Authors contributions

All authors contributed equally and approved the final version of the current manuscript.

Conflict of interest

The authors declare that they have no conflicts of interest.