Multiplicity of solutions to non-local problems of Kirchhoff type involving Hardy potential

1.   Introduction

Dual numbers were first given by Clifford (1845–1879), and some properties of those were studied in the geometrical investigation, and Kotelnikov ^[1] introduced their first applications. Study applied to line geometry and kinematics dual numbers and dual vectors ^[2]. He demonstrated that the directed lines of Euclidean 3-space and the points of the dual unit sphere in $\mathbb{D}^3$ have a one-to-one relationship. Field theory also relies heavily on these numbers ^[3]. The most intriguing applications of dual numbers in field theory are found in a number of Wald publications ^[4]. Dual numbers have contemporary applications in kinematics, dynamics, computer modeling of rigid bodies, mechanism design, and kinematics ^[5,6,7].

Complex numbers have significant advantages in derivative computations. However, the second derivative computations lost these advantages ^[8]. J. A. Fike developed the hyper-dual numbers to solve this issue ^[9]. These numbers may be used to calculate both the first and second derivatives while maintaining the benefits of the first derivative using complex numbers. Furthermore, it is demonstrated that this numerical approach is appropriate for open kinematic chain robot manipulators, sophisticated software, and airspace system analysis and design ^[10].

In the literature, sequences of integers have an important place. The most famous of these sequences have been demonstrated in several areas of mathematics. These sequences have been researched extensively because of their complex characteristics and deep connections to several fields of mathematics. The Fibonacci and Lucas sequences and their related numbers are of essential importance due to their various applications in biology, physics, statistics, and computer science ^[11,12,13]. Many authors were interested in introducing and investigating several generalizations and modifications of Fibonacci and Lucas sequences. The authors investigated two classes that generalize Fibonacci and Lucas sequences, and they utilized them to compute some radicals in reduced forms. Panwar ^[14] defined the generalized $k$-Fibonacci sequence as

with initial conditions $F_{k, 0} = a$ and $F_{k, 1} = b$. If $a = 0, k = 2, p = q = b = 1$, the classic Pell sequence and for $a = b = 2, k = 2, p = q = 1$, Pell-Lucas sequences appear.

The Pell numbers are the numbers of the following integer sequence:

The sequence of Pell numbers, which is denoted by ${P}_n$ is defined as the linear reccurence relation

The integer sequence of Pell-Lucas numbers denoted by ${Q}_n$ is given by

with the same reccurence relation

The characteristic equation of these numbers is $x^2-2x-1 = 0$, with roots $\alpha = 1+\sqrt{2}$ and $\beta = 1-\sqrt{2}$ and the Binet's forms of these sequences are given as^{[15,16,17,18]},

and

The set of dual numbers is defined as

The set of hyper-dual numbers is

or can be rewritten as

where $\varepsilon$, $\varepsilon^*$ and $\varepsilon\varepsilon^*$ are hyper-dual units that satisfy

This set forms commutative and associative algebra over both the dual and real numbers ^[8,9,10].

The square root of a hyper-dual number $\gamma$ can be defined by

A hyper-dual vector is any vector of the form

where $\vec{\gamma}_{0}, \vec{\gamma}_{1}, \vec{\gamma}_{2}, \vec{\gamma}_{3}$ are real vectors, this vector can be rewritten as $\vec{\gamma} = \vec{d}+\varepsilon^*\vec{d}^*$, where $\vec{d}$ and $\vec{d}^*$ are dual vectors. Let $\vec{\gamma}$ and $\vec{\delta}$ be hyper-dual vectors, then their scalar product is defined as

which continents inner products of real vectors.

Let $f(x_0+ x_1\varepsilon+ x_2\varepsilon^*+ x_3\varepsilon\varepsilon^*)$ be a hyper-dual function, then

Suppose $\vec{\gamma}$, $\vec{\delta}$ and $\Phi$ be unit hyper-dual vectors and hyper-dual angle respectively then by using (1.5) the scalar product can be written as

where $\phi$ and $\psi$ are, respectively, dual and real angles.

The norm of a hyper-dual vector $\vec{\gamma}$ is given by

for $\left\| \vec{\gamma}_0\right\|\neq0$. If $\left\| \vec{\gamma}\right\|_{HD} = 1$ that is $\left\| \vec{\gamma}_0\right\| = 1$ and $\langle \vec{\gamma}_0, \vec{\gamma}_1\rangle = \langle \vec{\gamma}_0, \vec{\gamma}_2\rangle = \langle \vec{\gamma}_0, \vec{\gamma}_3\rangle = \langle \vec{\gamma}_1, \vec{\gamma}_2\rangle = 0$, then $\vec{\gamma}$ is a unit hyper-dual vector.

In this paper, we introduce the hyper-dual Pell and the hyper-dual Pell-Lucas numbers, which provide a natural generalization of the classical Pell and Pell-Lucas numbers by using the concept of hyper-dual numbers. We investigate some basic properties of these numbers. We also define a new vector and angle, which are called hyper-dual Pell vector and angle. We give properties of these vectors and angles to exert in the geometry of hyper-dual space.

2.   Hyper-dual Pell and Hyper-dual Pell-Lucas numbers

In this section, we define the hyper-dual Pell and hyper-dual Pell-Lucas numbers and then demonstrate their fundamental identities and properties.

Definition 2.1. The $n^{th}$ hyper-dual Pell ${\mathrm{HP}}_n$ and hyper-dual Pell-Lucas ${\mathrm{HQ}}_n$ numbers are defined respectively as

and

where $\mathrm{P}_n$ and $\mathrm{Q}_n$ are $n^{th}$ Pell and Pell-Lucas numbers.

The few hyper-dual Pell and hyper-dual Pell-Lucas numbers are given as

and

Theorem 2.1. The Binet-like formulas of the hyper-dual Pell and hyper-dual Pell-Lucas numbers are given, respectively, by

and

where

Proof. From (2.1) and the Binet formula of Pell numbers, we obtain

On the other hand, using (2.2) and the Binet formula of Pell-Lucas numbers we obtain

□ The proof is completed.

Theorem 2.2. (Vajda-like identities) For non-negative integers m, n, and r, we have

Proof. By using the Binet-like formula of hyper-dual Pell numbers, we obtain

and by using (1.1), we obtain

Similarly for hyper-dual Pell-Lucas numbers, we can obtain

Using (1.2) and (2.5),

Thus, we obtain the desired results. □

Theorem 2.3. (Catalan-like identities) For non negative integers n and r, with $n\ge r$, we have

Proof. From (2.3), we obtain

and by using (1.1) and (2.5), we will have

On the other hand, from (2.4) and (2.5) we obtain

□

Corollary 2.1. (Cassini-like identities) For non-negative integer n, we have

Proof. We can get the result by taking $r = 1$ in Theorem 2.3. □

Theorem 2.4. (d'Ocagne-like identities) For non-negative integers n and m,

Proof. Using (1.1), (2.3), and (2.5), we have

Using (1.2), (2.4) and (2.5), we have

□

3.   Hyper dual Pell vectors and angle

In this section, we introduce hyper-dual Pell vectors and hyper-dual Pell angle. We will give geometric properties of them.

Definition 3.1. The $n^{th}$ hyper-dual Pell vector is defined as

where $\vec{\mathrm{P}}_{n} = (\mathrm{P}_n, \mathrm{P}_{n+1}, \mathrm{P}_{n+2})$ is a real Pell vector. The hyper-dual Pell vector $\overrightarrow{\mathrm{HP}}_n$ can be rewritten in terms of dual Pell vectors $\vec{\mathbb{P}}_n$ and $\vec{\mathbb{P}} ^*_{n}$ as

Theorem 3.1. The scalar product of hyper-dual Pell vectors $\overrightarrow{{\mathrm{HP}}}_n$ and $\overrightarrow{{\mathrm{HP}}}_m$ is

Proof. By using (1.4), we can write

Now we calculate the above inner products for real Pell vectors $\vec{\mathrm{P}}_{n}$ and $\vec{\mathrm{P}}_{m}$ by using Binet's formula of Pell numbers as

□ Similarly,

By substituting these equalities in (3.2), we obtain the result.

Example 3.1. Let $\overrightarrow{{\mathrm{HP}}}_1 = (1, 2, 5)+(2, 5, 12)\varepsilon+(5, 12, 29)\varepsilon^*+(12, 29, 70)\varepsilon\varepsilon^*$ and $\overrightarrow{{\mathrm{HP}}}_0 = (0, 1, 2)+(1, 2, 5)\varepsilon+(2, 5, 12)\varepsilon^*+(5, 12, 29)\varepsilon\varepsilon^*$ be the hyper-dual Pell vectors. The scalar product of $\overrightarrow{{\mathrm{HP}}}_1$ and $\overrightarrow{{\mathrm{HP}}}_0$ are

By the other hand

The results are the same as we expected.

Corollary 3.1. The norm of $\overrightarrow{{\mathrm{HP}}}_n$ is

Proof. The proof is clear from taking $m = n$ in (3.1). □

Example 3.2. Find the norm of $\overrightarrow{{\mathrm{HP}}}_1 = (1, 2, 5)+(2, 5, 12)\varepsilon+(5, 12, 29)\varepsilon^*+(12, 29, 70)\varepsilon\varepsilon^*$.

If we take $n = 1$ in (3.3) and use (1.3), then we will get

From (1.6) and (3.1), the following cases can be given for the scalar product of hyper-dual Pell vectors $\overrightarrow{\mathrm{HP}}_n$ and $\overrightarrow{\mathrm{HP}}_m$.

Case 3.1. Assume that $\cos\phi = 0$ and $\phi^{\ast }\neq 0$, then $\psi = \frac{\pi}{2}$, $\psi^* = 0$, therefore

then, we get

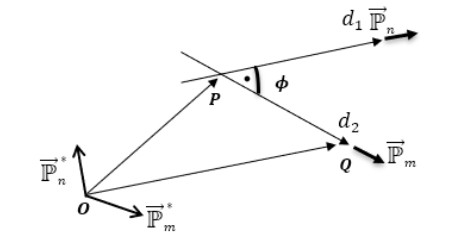
and corresponding dual lines $\mathrm{}{d}_1$ and ${d}_2$ are perpendicular such that they do not intersect each other; see Figure 1.

Case 3.2. Assume that $\phi^{\ast } = 0$ and $\phi\neq0$, then we obtain

therefore

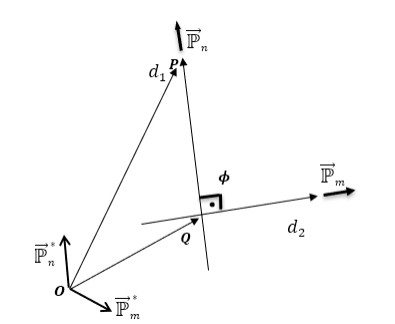
and corresponding dual lines ${d}_1$ and ${d}_2$ intersect each other; see Figure 2.

Case 3.3. Assume that $\cos\phi = 0$ and $\phi^* = 0$, then $\psi = \frac{\pi}{2}$ and $\psi^{\ast } = 0$, therefore

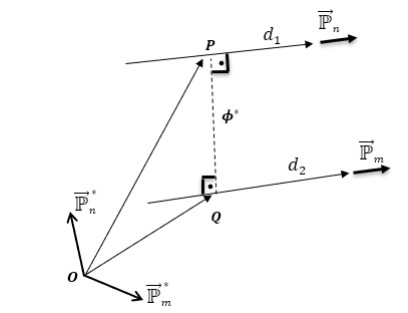
and dual lines ${d}_1$ and ${d}_2$ intersect each other at a right angle; see Figure 3.

Case 3.4. Assume that $\phi = 0$ and $\phi^* = 0$, then

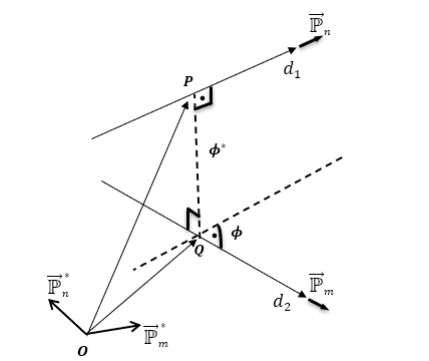
in this case corresponding dual lines ${d}_1$ and ${d}_2$ are parallel; see Figure 4.

4.   Conclusions

In the present study, we introduce two families of hyper-dual numbers with components containing Pell and the Pell-Lucas numbers. First, we define hyper-dual Pell and Pell-Lucas numbers. Afterwards, by means of the Binet's formulas of Pell and Pell-Lucas numbers, we investigate identities such as the Binet-like formulas, Vajda-like, Catalan-like, Cassini-like, and d'Ocagne-like identities. After that, we define hyper-dual Pell vector and angle with some properties and geometric applications related to them. In the future it would be valuable to replicate a similar exploration and development of our findings on hyper-dual numbers with Pell and Pell-Lucas numbers. These results can trigger further research on the subjects of the hyper-dual numbers, vector, and angle to carry out in the geometry of dual and hyper-dual space.

Author contributions

Faik Babadağ and Ali Atasoy: Conceptualization, writing-original draft, writing-review, editing. All authors have read and approved the final version of the manuscript for publication.

Conflict of interest

The authors declare that they have no conflict of interest.