Global attractive periodic solutions of neutral-type neural networks with delays in the leakage terms

1.   Introduction

In this paper, we are devoted to investigating a class of neutral-type neural networks with delay in the leakage terms as follows:

where $i = 1, 2, \cdots, n, \; a_i, b_i$ and $d_{ij}$ are positive constants, $\sigma, \tau > 0$ are constant delays, $c_i(t), \; \gamma(t)$ and $I_i(t)$ are $\omega$-periodic continuous functions, $h_i\in C(\mathbb{R}^+, \mathbb{R}^+), \; f_j(\cdot)\in C(\mathbb{R}, \mathbb{R}), \; \mathbb{R}^+ = [0, \infty)$. For more detailed practical significance of system (1.1), refer to ^[1,2,3].

Leakage delay or forgetting delay widely exists in network systems, and its research has important practical value. In 2007, Gopalsamy ^[2] studied the following BAM neural networks with constant delays in the leakage terms:

where $x_i(t-\tau_i^{(1)})$ and $y_i(t-\tau_i^{(2)})$ are leakage terms, $\tau_i^{(1)}$ and $\tau_i^{(2)}$ are called leakage delays. Li and Cao ^[4] considered delay-dependent stability of neutral-type neural networks with delay in the leakage term as follows:

where $x(t-\sigma)$ is leakage term, $\sigma$ is leakage delay. System (1.2) only contains constant delay, system (1.3) contains mixed delays including time-varying delays and continuously distributed delays. Peng ^[5] investigated the existence and global attractivity of periodic solutions for BAM neural networks with continuously distributed delays in the leakage terms:

where $x_i(t-s)$ and $y_j(t-s)$ are leakage terms. In ^[6], the authors considered existence, uniqueness and the global asymptotic stability of fuzzy cellular neural networks with mixed delays by using the Lyapunov method and the linear matrix inequality approach. For more results about neural networks with delays in the leakage terms, see e.g ^{[7,8,9,10,11]}.

The dynamic characteristics of the neutral-type neural networks with delay in the leakage terms have been widely studied and can be applied in various fields such as artificial neural networks, intelligent fuzzy recognition, automatic control, etc. In addition, due to the limited speed of information processing, the existence of time delays often leads to oscillation, divergence, or instability of neural networks. Therefore, It is important to consider the impact of delay on network stability. Many authors have extensively studied networks with various types of delays, see ^{[12,13,14,15,16]}. Neutral-type neural networks is a system which its delay term contains derivative. In fact, many dynamic systems can be modelled as neutral-type differential systems. Due to the fact that neutral-type systems are more extensive and complex than non neutral systems, they have always been a hot topic of research. Kong and Zhu ^[17] discussed the finite-time stabilization of a class of discontinuous fuzzy neutral-type neural networks with multiple time-varying delays. Zhang et al. ^[18] studied synchronization control of neutral-type neural networks with sampled-data via adaptive event-triggered communication scheme. Karthick et al. ^[19] investigated memory feedback finite-time control for memristive neutral-type neural networks with quantization by using proper Lyapunov Krasovskii functional and linear matrix inequalities. System (1.1) shows the neutral character by the operator $(A_ix_i)(t) = x_i(t)-c_i(t)x_i(t-\sigma), \; i = 1, \cdots, n$, which is a $D$-operator form, see ^[20]. System (1.3) shows the neutral character by the term $Dx'(t-h(t))$ which is different from one in system (1.1). Since the $D$-operator $(A_ix_i)(t)$ has many important properties, we can conveniently use these properties to study system (1.1). For more results about neutral-type neural networks, see ^{[21,22,23,24]}.

We give the main contributions of this paper as follows:

(1) We first study a class neutral-type neural networks with time delay in the leakage term and $D$-operator form which is deferent from the existing neutral-type neural networks, see ^[18,19].

(2) System (1.1) includes leakage constant delays, time-varying delays and continuously distributed delays which generalizes the corresponding ones of ^[3,4,5]. The neural networks with leakage delays has extensive applications in real world. Therefore, our study has important practical value.

(3) Using properties of neutral-type operators, coincidence degree theory, Lyapunov functional method we obtain existence and global attractivity of periodic solutions to system (1.1). Our main results are also valid for the case of non neutral-type neural networks. The research methods in this paper can be used other type dynamic systems and neural networks.

The remainder of this paper are organized as follows: Section 2 gives some basic lemmas which can be used in this paper. In Section 3, we obtain some sufficient conditions for existence of periodic solution of system (1.1). Section 4 gives some sufficient conditions for guaranteeing the global attractivity of periodic solution of system (1.1). In Section 5, an example is given to show the effectiveness of the main results. Finally, some conclusions and discussions are given.

2.   Preliminaries

Let $\mathbb{X}$ and $\mathbb{Y}$ be two Banach spaces. Let $\mathcal{L}:D(\mathcal{L})\subset \mathbb{X}\rightarrow \mathbb{Y}$ be a Fredholm operator with index zero which means that $Im\mathcal{L}$ is closed in $\mathbb{Y}$ and $dimKer\mathcal{L} = codimIm\mathcal{L} < +\infty$. Let projectors $P:\mathbb{X}\rightarrow \mathbb{X}, \; Q:\mathbb{Y}\rightarrow \mathbb{Y}$ such that $ImP = Ker\mathcal{L}, \; Im\mathcal{L} = KerQ$. Furthermore, $\mathcal{L}_{D(\mathcal{L})\cap KerP}:(I-P)\mathbb{X}\rightarrow Im\mathcal{L}$ is invertible. Denote by $K_p$ the inverse of $\mathcal{L}_P$.

Let $\Omega$ be an open bounded subset of $\mathbb{X}$. Let the operator $\mathcal{N} :\bar{\Omega}\rightarrow \mathbb{Y}$ be $\mathcal{L}$-compact in $\bar{\Omega}$ which means that $Q\mathcal{N}(\bar{\Omega})$ is bounded and the operator $K_p(I-Q)\mathcal{N}(\bar{\Omega})$ is relatively compact. We first give the famous Mawhin's continuation theorem.

Lemma 2.1. ^[25] Assume that $\mathbb{X}$ and $\mathbb{Y}$ are two Banach spaces, and $\mathcal{L}:D(\mathcal{L})\subset \mathbb{X}\rightarrow \mathbb{Y},$ is a Fredholm operator with index zero. Furthermore, $\Omega\subset \mathbb{X}$ is an open bounded set and $\mathcal{N}:\bar{\Omega}\rightarrow \mathbb{Y}$ is $L$-compact on $\bar{\Omega}$. If all the following conditions hold:

(1) $\mathcal{L}x\neq\lambda \mathcal{N}x, \mbox\forall x\in\partial\Omega\cap D(\mathcal{L}), \forall \lambda\in(0, 1),$

(2) $\mathcal{N}x\notin Im\mathcal{L}, \mbox\forall x\in\partial\Omega\cap Ker\mathcal{L},$

(3) $deg\{Q\mathcal{N}, \Omega\cap Ker\mathcal{L}, 0\}\neq 0$.

Then equation $\mathcal{L}x = \mathcal{N}x$ has a solution on $\bar{\Omega}\cap D(\mathcal{L}).$

Let $C_T = \{x:x\in C(\mathbb{R}, \mathbb{R}), x(t+T)\equiv x(t)\}$ with the norm $||x|| = \max_{t\in[0, T]}|x(t)|$. Obviously, $C_T$ is a Banach space.

Lemma 2.2. ^[26] Let

where $C_T$ is a $T-$periodic continuous function space, $c(t)\in C_T$, $\tau > 0$ is a constant. If $|c(t)|\neq1$, then operator $A$ has continuous inverse $A^{-1}$ on ${C}_T$, satisfying

(1)

(2)

(3)

where $c_0 = \max_{t\in[0, T]}|c(t)|, \; \sigma = \min_{t\in[0, T]}|c(t)|.$ Throughout this paper, let

with the norm $||x|| = \max_{i = 1, \cdots, n}|x_i|_0$, $x = (x_1, \cdots, x_n)^T\in\mathbb{R}^n, \; |x_i|_0 = \max_{t\in[0, T]}|x_i(t)|$.

3.   Existence of periodic solutions

For the sake of convenience, we list the following conditions.

(H$_1$) There exists $p_j > 0$ such that

(H$_2$) There exists a constant $D > 0$ such that

Theorem 3.1. Suppose that $\int_0^\infty h_i(s)ds = 1, \; \int_0^TI_i(s)ds = 0$, $\int_0^T\psi(s)\psi^T(s)ds\neq{\bf 0}$, $|c_i(t)|\neq1, \; 1-\gamma'(t) > 0$ for all $t\in \mathbb{R}$, and assumptions ${\rm(H_1)–(H_2)}$ hold, where $\psi(t)$ is defined by (3.6). Then system (1.1) has at least one $T$-periodic solution, if

or if

where $c_0 = \max|c_i(t)|, \; \breve{c} = \min|c_i(t)|, \; \tilde{c} = \max|c_i'(t)|, \; t\in\mathbb{R}, \; i = 1, \cdots, n.$

Proof. Let $(A_ix_i)(t) = x_i(t)-c_i(t)x_i(t-\sigma), \; i = 1, \cdots, n$. System (1.1) can be rewritten by the following system:

Let

where

Define $\mathcal{N}:\bar{\Omega}\subset\mathbb{X}\rightarrow \mathbb{Y}$ by

where $(\mathcal{N}x)(t) = ((\mathcal{N}_1x_1)(t), \cdots, (\mathcal{N}_nx_n)(t))^T$. Thus, system (3.3) is equivalent to the following operator system:

where $\mathcal{L}_i$ and $\mathcal{N}_i$ are defined by (3.4) and (3.5), respectively. Obviously, $Im\mathcal{L} = \{y:y\in\mathbb{Y}, \; \int_0^Ty(t)dt = {\bf 0}\}$. For each $x\in Ker\mathcal{L}$, we get $\big(x(t)-c(t)x(t-\sigma)\big)' = {\bf 0}$. Without loss of generality, let

where $I$ is a $n\times n$ identity matrix. Let $\psi(t)\in\mathbb{R}^n$ be the unique $T-$periodic solution of (3.6), then $\psi(t)\neq{\bf 0}$ and $Ker\mathcal{L} = \{a\psi(t):a\in\mathbb{R}^n\}$. It is to see that $Im\mathcal{L}$ is closed in $\mathbb{Y}$ and $\mbox{dimKer}\mathcal{L} = \mbox{codimIm}\mathcal{L} = n$. So $\mathcal{L}$ is a Fredholm operator with index zero. Define continuous projectors $P$ and $Q$ by, respectively,

and

where $\psi$ is defined by (3.6). Let

then

Since $K_p$ is an embedding operator, then $K_p$ is a completely operator in $\mbox{Im}\mathcal{L}$. By the definitions of $Q$ and $\mathcal{N}$, it knows that $Q\mathcal{N}(\bar{\Omega})$ is bounded on $\bar{\Omega}$. Hence nonlinear operator $\mathcal{N}$ is $\mathcal{L}$-compact on $\overline{\Omega}$.

For any $\lambda\in(0, 1), \; i = 1, \cdots, n$, consider the following operator system:

i.e.,

Integrating both sides of (3.7) on $[0, T]$, one can see

where $\tilde{\gamma}(t)$ is a inverse function of $t-\gamma(t)$. We claim that there exists a point $t_1\in[0, T]$ such that

where $D$ is defined by assumption (H$_2$). If $|x(t)| > D$ for all $t\in[0, T]$, then by assumption (H$_2$) we get

which contradicts (3.8). Hence, (3.9) holds. From (3.9) and assumption (H$_1$), one can see

and

From $(A_ix_i)(t) = x_i(t)-c_i(t)x_i(t-\sigma)$, we have

If $c_0 < \frac{1}{2}$, in view of Lemma 2.2, (3.11) and (3.12), we have

From (3.10) and (3.13), we have

It follows by (3.1) and (3.14) that

On the other hand, if $\breve{c} > 1$, similarly to the above proof, by (3.2), there exists a constant $M_2 > 0$ such that

From (3.15) and (3.16), we have

Let $\Omega_1 = \{x\in Ker\mathcal{L}:Q\mathcal{N}x = {\bf 0}\}$. We show that $\Omega_1$ is a bounded set. For each $x\in\Omega_1$, there exists $x_i = \eta_i\psi_i(t)$ such that

where $i = 1, \cdots, n, \eta_i\in\mathbb{R}.$ When $c_0 < \frac{1}{2}$, we have

Then, we have $\eta_i\leq\frac{D}{\gamma_1}$. Otherwise, for all $t\in[0, T]$, we have $\eta_i\psi_i(t) > D$ and

which contradicts (3.18). On the other hand, when $\breve{c} > 1$, we have

Then, we have $\eta_i\leq-\frac{D}{\gamma_2}$. Otherwise, for all $t\in[0, T]$, we have $\eta_i\psi_i(t) < -D$ and

which contradicts (3.18). Hence, $\Omega_1$ is a bounded set. Denote

where $M_3$ is defined by (3.17). Let $\Omega = \{x\in\mathbb{X}:||x|| < M\}$. From the above proof, conditions (1) and (2) of Lemma 2.1 hold. Now, we show that condition (3) of Lemma 2.1 holds. Take the homotopy

We claim that

If (3.19) does not hold, then

Since $|x_i| > D$, then (3.20) does not holds. Hence, (3.19) holds. So we have

So, condition (3) of Lemma 2.1 holds. Applying Lemma 2.1, we reach the conclusion. □

Remark 3.1. Lemma 2.1 is critical for estimating the prior bound of solution to system (1.1). In this section, we obtain the existence results of periodic solutions when the neutral operator is stable ($|c_i(t)| < 1$) or unstable ($|c_i(t)| > 1$). Therefore, the existence results of this article have broader theoretical and practical value.

4.   Global attractivity of periodic solutions

For any $t_0\geq0$, we give the initial conditions associated with system (1.1) as follows:

where $\phi_i\in C((-\infty, t_0), \mathbb{R})$ and $||\phi|| < \infty$.

Definition 4.1. Suppose that $\bar{x}(t) = (\bar{x}_1(t), \cdots, \bar{x}_n(t))^T$ is a periodic solution of system (1.1), and ${x}(t) = ({x}_1(t), \cdots, {x}_n(t))^T$ is a any solution of system (1.1). Let $u_i(t) = x_i(t)-\bar{x}_i(t), \; i = 1, \cdots, n$. If

we call $\bar{x}(t)$ is globally attractive.

Theorem 4.1. Assume that all conditions of Theorem 3.1 hold and $\int_0^\infty sh_i(s)ds < \infty$. Suppose that

(H$_3$) There exists $L_j > 0$ such that

Then system (1.1) has an $T$-periodic solution which is globally attractive provided that

where $i = 1, \cdots, n, \; \xi_i = \int_0^\infty sh_i(s)ds, \; \alpha_i = \sum_{j = 1}^nd_{ij}L_j,$

$\omega(t) = \frac{1}{1-\gamma'(\tilde{\gamma}(t))}, \; \tilde{\gamma}(t)$ is an inverse function of $t-\gamma(t)$.

Proof. From Theorem 3.1, system (1.1) has a $T-$periodic solution $\bar{x}(t) = (\bar{x}_1(t), \cdots, \bar{x}_n(t))^T$. Suppose that ${x}(t) = ({x}_1(t), \cdots, {x}_n(t))^T$ is a any solution of system (1.1). Let

For $t\geq t_0$, we have

Let

Derivation of (4.4) along the solution of (4.3) gives

From (4.5) and a lengthy simplification (by using $a^2+b^2\geq2ab$), we have

Let

From (4.7)–(4.11), we have

Construct the following Lyapunov functional:

From (4.6) and (4.12)–(4.17), we have

where $q_i$ is defined by (4.2). In view of (4.1), we can see $V(t_0) < \infty$. Thus,

and

Therefore,

and

where $\Xi = \max\{\frac{1}{1-c_0}, \frac{1}{\breve{c}-1}\}$. Since $V(t_0)$ can be made arbitrarily small for sufficient small initial values, it follows by (4.19) that the solution of system (1.1) is uniformly bounded on $[t_0, \infty)$. By (4.19) we have

In view of Barbalat's lemma (see Gopalsamy ^[27]), we get

This completes the proof of the global attractivity of $T$-periodic solution of system (1.1). □

Remark 4.1. Since there is no fixed method for constructing Lyapunov functional, constructing proper Lyapunov functional is very difficult. In this section, utilizing the properties of neutral operators, we construct a new Lyapunov functional which has important application for the proof of Theorem 4.1.

5.   Example

Consider the following two-neuron neural networks with delay in the leakage terms:

where

Obviously, we have

When $c_0 = 0.01 < \frac{1}{2}$, we have

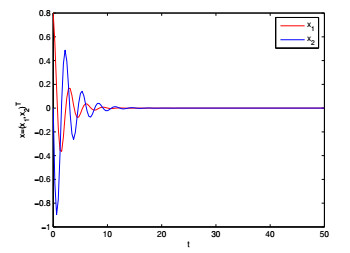
Thus, condition (3.1) in Theorem 3.1 holds and system (5.1) exists a periodic solution $x = (0, 0)^T$. Furthermore, we have $q_1\approx0.122 > 0$ and $q_2\approx0.113 > 0$ and condition (4.2) in Theorem 4.1 holds and the periodic solution $x = (0, 0)^T$ of system (5.1) is globally attractive. Figure 1 shows that the state trajectory of the system (5.1). From Figure 1, we find that the periodic solution $x = (0, 0)^T$ of system (5.1) is globally attractive which verifies the correctness of the conclusions of Theorems 3.1 and 4.1.

6.   Conclusions

In this paper, we have dealt with the existence and global attractivity of periodic solution to a class of neutral-type neural networks with delay in the leakage terms. System (1.1) contains mixed delays including leakage constant delays, time-varying delays and continuously distributed delays. As is well known, delay has a fundamental impact on the dynamic behavior of network systems. The leakage delay is a special type of delay, and its research has important theoretical and practical value. From main results of this paper, we find that the leakage term has great impact on the dynamical properties of neural networks. our results greatly generalize the corresponding ones of ^[3,4,5,6]. Based on coincidence degree theory and the Lyapunov functional, some sufficient conditions ensuring the existence, and global attractivity of periodic solution have been presented. It should be pointed out that by utilizing the properties of neutral operators, we have constructed a new Lyapunov functional that can conveniently obtain the dynamic behavior of periodic solutions. A numerical example has been illustrated to demonstrate the usefulness of the proposed method. The research method in this article can be used to study various types of systems, neutral-type neural networks with delay in the leakage terms, for example, neutral-type neural networks with impulses and delay in the leakage terms, neutral-type neural networks with stochastic disturbances and delay in the leakage terms, and so on.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This paper is supported by Anhui University Natural Sciences fund: Kj2019A0703.

Conflict of Interest

The authors declare no conflict of interest.