1.
Introduction
The convexity of function is a classical concept, since it plays a fundamental role in mathematical programming theory, game theory, mathematical economics, variational science, optimal control theory and other fields, a new branch of mathematics, convex analysis, appeared in the 1960s. However, it has been noticed that the functions encountered in a large number of theoretical and practical problems in economics are not classical convex functions, therefore, in the past decades, the generalization of function convexity has attracted the attention of many scholars and aroused great interest, such as h-convex functions [1,2,3,4,5], log-convex functions [6,7,8,9,10], log-h-convex functions [11], and especially for coordinated convex [12]. Since 2001, various extensions and generalizations of integral inequalities for coordinated convex functions have been established in [12,13,14,15,16,17].
On the other hand, calculation error has always been a troublesome problem in numerical analysis. In many problems, it is often to speculate the accuracy of calculation results or use high-precision operation as far as possible to ensure the accuracy of the results, because the accumulation of calculation errors may make the calculation results meaningless, interval analysis as a new important tool to solve uncertainty problems has attracted much attention and also has yielded fruitful results, we refer the reader to the papers [18,19]. It is worth notion that in recent decades, many authors have combined integral inequalities with interval-valued functions(IVFs) and obtained many excellent conclusions. In [20], Costa gave Opial-type inequalities for IVFs. In [21,22], Chalco-Cano investigated Ostrowski type inequalities for IVFs by using generalized Hukuhara derivative. In [23], Román-Flores derived the Minkowski type inequalities and Beckenbach's type inequalities for IVFs. Very recently, Zhao [5,24] established the Hermite-Hadamard type inequalities for interval-valued coordinated functions.
Motivated by these results, in the present paper, we introduce the concept of coordinated log-h-convex for IVFs, and then present some new Jensen type inequalities and Hermite-Hadamard type inequalities for interval-valued coordinated functions. Also, we give some examples to illustrate our main results.
2.
Preliminaries
Let RI the collection of all closed and bounded intervals of R. We useR+IandR+ to represent the set of all positive intervals and the family of all positive real numbers respectively. The collection of all Riemann integrable real-valued functions on [a,b], IVFs on [a,b] and IVFs on △=[a,b]×[c,d] are denoted by R([a,b]), IR([a,b]) and ID(△). For more conceptions on IVFs, see [4,25]. Moreover, we have
Theorem 1. [4] Let f:[a,b]→RI such that f=[f_,¯f]. Then f∈IR([a,b]) iff f_, ¯f∈R([a,b]) and
Theorem 2. [25] Let F:△→RI. If F∈ID(△), then
Definition 1. [26] Let h:[0,1]→R+. We say that f:[a,b]→R+I is interval log-h-convex function or that f∈SX(log-h,[a,b],R+I), if for all x,y∈[a,b] and ϑ∈[0,1], we have
h is called supermultiplicative if
for all ϑ,τ∈[0,1]. If "≥" in (2.1) is replaced with "≤", then h is called submultiplicative.
Theorem 3. [26] Let F:[a,b]→R+I,h(12)≠0. If F∈SX(log-h,[a,b],R+I) and F∈IR([a,b]), then
Theorem 4. [27] Let F:[a,b]→R+I,h(12)≠0. If F∈SX(log-h,[a,b],R+I) and F∈IR([a,b]), then
3.
Main results
In this section, we define the coordinated log-h-convex for IVFs and prove some new Jensen type inequalities and Hermite-Hadamard type inequalities by using this new definition.
Definition 2. Let h:[0,1]→R+. Then F:△→R+I is called a coordinated log-h-convex IVFs on △ if the partial mappings
are log-h-convex for all y∈[c,d] and x∈[a,b]. Then the set of all coordinated log-h-convex IVFs on △ is denoted by SX(log-ch,△,R+I).
Definition 3. Let h:[0,1]→R+. Then F:△→R+ is called a coordinated log-h-convex function in △ if for any (x1,y1),(x2,y2)∈△ and ϑ∈[0,1] we have
The set of all log-h-convex functions in △ is denoted by SX(log-h,△,R+). If inequality (3.1) is reversed, then F is said to be a coordinated log-h-concave function, the set of all log-h-concave functions in △ is denoted by SV(log-h,△,R+).
Definition 4. Let h:[0,1]→R+. Then F:△→R+I is called a coordinated log-h-convex IVF in △ if for any (x1,y1),(x2,y2)∈△ and ϑ∈[0,1] we have
The set of all log-h-convex IVFs in △ is denoted by SX(log-h,△,R+I).
Theorem 5. Let F:△→R+I such that F=[F_,¯F]. If F∈SX(log-h,△,R+I) iff F_∈SX(log-h,△,R+) and ¯F∈SV(log-h,△,R+).
Proof. The proof is completed by combining the Definitions 3 and 4 above and the Theorem 3.7 of [4].
Theorem 6. If F∈SX(log-h,△,R+I), then F∈SX(log-ch,△,R+I).
Proof. Assume that F∈SX(log-h,△,R+I). Let Fx:[c,d]→R+I,Fx(y)=F(x,y). Then for all ϑ∈[0,1] and y1,y2∈[c,d], we have
Hence Fx(y)=F(x,y) is log-h-convex on [c,d]. The fact that Fy(x)=F(x,y) is log-h-convex on [a,b] goes likewise.
Remark 1. The converse of Theorem 6 is not generally true. Let h(ϑ)=ϑ and ϑ∈[0,1], △1=[π4,π2]×[π4,π2], and F:△1→R+I be defined:
Obviously, we have that F∈SX(log-ch,△1,R+I) and F∉SX(log-h,△1,R+I). Indeed, if (π4,π2),(π2,π4)∈△1, we have
If ϑ=0, then
Thus, F∉SX(log-h,△1,R+I).
In the following, Jensen type inequalities for coordinated log-h-convex functions in △ is considered.
Theorem 7. Let pi∈R+,xi∈[a,b],yi∈[c,d],(i=1,2,...,n),F:△→R+. If h is a nonnegative supermultiplicative function and F∈SX(log-h,△,R+), then
where Pn=n∑i=1pi. If h is a nonnegative submultiplicative function and F∈SV(log-h,△,R+), then (3.2) is reversed.
Proof. If n=2, then from Definition 3, we have
Suppose (3.2) holds for n=k, then
Now, let us prove that (3.2) is valid when n=k+1,
This completes the proof.
Remark 2. If h(ϑ)=ϑ, then the inequality (3.2) is the Jensen inequality for log-convex functions.
Now, we prove the Jensen inequality for log-h-convex IVFs in △.
Theorem 8. Let pi∈R+,xi∈[a,b],yi∈[c,d],i=1,2,...,n,F:△→R+I such that F=[F_,¯F]. If h is a nonnegative supermultiplicative function and F∈SX(log-h,△,R+I), then
where Pn=n∑i=1pi. If F∈SV(log-h,△,R+I), then (3.3) is reversed.
Proof. By Theorem 5 and Theorem 7, we have
and
Thus,
This completes the proof.
Next, we prove the Hermite-Hadamard type inequalities for coordinated log-h-convex IVFs.
Theorem 9. Let F:△→R+I and h:[0,1]→R+ be continuous. If F∈SX(log-ch,△,R+I), then
Proof. Since F∈SX(log-ch,△,R+I), we have
That is,
Moreover, we have
Similarly, we get
Then
That is,
Integrating over [a,b], we have
Similarly, we have
Finally, we obtain
This concludes the proof.
Remark 3. If F_=¯F and h(ϑ)=ϑ, then Theorem 9 reduces to Corollary 3.1 of [13].
Example 1. Let [a,b]=[c,d]=[2,3],h(ϑ)=ϑ. We define F:[2,3]×[2,3]→R+I by
From Definition 2, F(x,y)∈SX(log-ch,△,R+I).
Since
and
It follows that
and Theorem 9 is verified.
Theorem 10. Let F:△→R+I and h:[0,1]→R+ be continuous. If F∈SX(log-ch,△,R+I), then
Proof. Since F∈SX(log-ch,△,R+I), by using Theorem 6 and (2.3), we have
That is,
Moreover, we have
Similarly, we have
We also from (2.2),
Again from (2.3),
and proof is completed.
Example 2. Furthermore, by Example 1, we have
and
It follows that
and Theorem 10 is verified.
4.
Conclusions
We introduced the coordinated log-h-convexity for interval-valued functions, some Jensen type inequalities and Hermite-Hadamard type inequalities are proved. Our results generalize some known inequalities and will be useful in developing the theory of interval integral inequalities and interval convex analysis. The next step in the research direction investigated inequalities for fuzzy-interval-valued functions, and some applications in interval nonlinear programming.
Acknowledgments
The first author was supported in part by the Key Projects of Educational Commission of Hubei Province of China (D20192501), the Natural Science Foundation of Jiangsu Province (BK20180500) and the National Key Research and Development Program of China (2018YFC1508100).
Conflict of interest
The authors declare no conflict of interest.









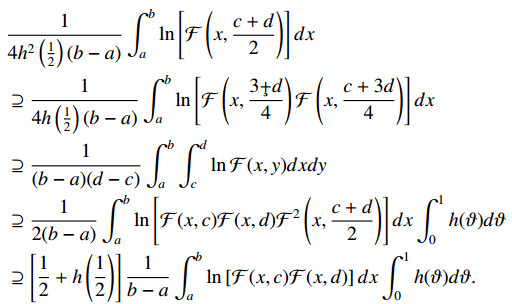











 DownLoad:
DownLoad: