Dynamic analysis and optimal control of Zika virus transmission with immigration

1.   Introduction

Zika virus belongs to flavivirus genus, flavivirus family, which is an arbovirus transmitted by mosquitoes, mostly transmitted by Aedes aegypti, Aedes albopictus and Culex mosquitoes, etc. Zika virus was first detected in rhesus monkeys in the Zika jungle in Uganda in 1947 ^[1], and then in 1952, first found in populations in Uganda ^[2]. During 2015 and 2016, Brazil reported more than 4,000 cases of microcephalic teratoma in pregnant women infected with Zika virus ^[3,4], a 20 fold increase compared to previous years. By early 2016, Zika virus has spread to South America, Asia, Oceania and other regions ^[5,6,7]. According to the World Health Organization, 86 countries and territories have experienced outbreaks of the Zika virus since the outbreak began.

Human immigration is a very normal phenomenon. The movement or travel of a group of people, either from an endemic area to a healthy area or from a healthy area to an endemic area. Therefore, population movement or immigration is the main cause of the rapid spread of infectious diseases. Fred Brauer et al. ^[8] considered the immigration of infected individuals based on the traditional SI and SIS models of infectious diseases and assumed a constant rate of population immigration. Their results suggest that isolation of migrating infected individuals is necessary. Molalegn Ayana and Purnachandra Rao Koya ^[9] considered the impact of having immigrants infected with Zika virus through a model and proposed that infected immigrants facilitate the spread of Zika virus. Traoré et al. ^[10] analyzed a vector-borne infectious disease model that takes into account vector and human immigration. Their results also indicate that human migration is a problem that cannot be ignored and may cause the spread of disease in non-infected areas. So what control measures are more appropriate for this situation? Should we take immigration testing or require pre-migration vaccination?

There are many scholars who have focused their research on optimal cost-effectiveness and cost analysis. Kouidere et al. ^[11] studied a mathematical model that describes the transmission dynamics of African swine fever virus (ASFV) between pigs and ticks. To reduce the number of infected pigs and ticks, several strategies are proposed, and Pontryagin's Maximum principle and cost analysis are used to find the solution of optimal control. In 2022, they proposed a mathematical model in another paper ^[12] to describe the spread of COVID-19 in Peru, and characterized the optimal control through Pontryagin's Maximum principle. Using an optimal control model, Abdulfatai and Armin ^[13] concluded that by comparing treatment of symptomatic infected individuals and indoor residual spraying is the most cost-effective strategy. Miyaoka et al. ^[14] developed a response-diffusion model of Zika transmission, suggesting that the best control strategy is to immunize susceptible populations with vaccination as the control variable. Bonyah Ebenezer et al. ^[15] proposed and analyzed a SEIR-Zika epidemic model and established an optimal control model. They only proposed the optimal control strategy and did not mention the cost. Similarly, there are a number of studies that consider only optimal control strategies ^{[16,17,18,19]}. Screening controls for in-migrants are largely absent from these control strategies. As of now, there is some wait time for a Zika virus vaccine to become available, but testing for Zika virus is currently available. The major contributions of this work are as follows: A Zika virus model with immigrants is proposed to explain the risk of virus transmission by immigrants. We also propose appropriate screening measures for immigrants to find the optimal control scheme by building an optimal control model as well as cost analysis, pointing out the feasibility of appropriate screening in Zika virus control.

The structure of this paper is as follows. In the next section, the Zika virus model with immigration is proposed. In Section 3, we discussed the stability of the equilibriums point. In Section 4, combining with the actual situation, the control strategy is proposed and the optimal control model is established. The optimal control analysis is carried out. Cost-effectiveness analysis is given in Section 5. Then, the conclusion and discussion will be made in Section 6.

2.   Establishment of the model

Considering that mosquitoes move in a relatively small distance, we overlook the immigration of mosquitoes. We divide the human population into four sub-classes, namely susceptible humans $S_{H}$, exposed humans $E_{H}$, infected humans $I_{H}$, and recovered humans $R_{H}$. By this virtue, the total human population can be represented by: $N_{H} = S_{H}+E_{H}+I_{H}+R_{H}.$ Similarly, $N_{M}(t)$ is the total number of mosquitoes, which can be rationally partitioned into susceptible mosquitoes $S_{M}$, exposed mosquitoes $E_{M}$, infected mosquitoes $I_{M}$. Hence, $N_{M} = S_{M}+E_{M}+I_{M}.$

One problem for the model proposed by Molalegn Ayana and Purnachandra Rao Koya ^[9] is that if there are no infected people in the current infected population, then no one in the immigrant population is infected, which is clearly inappropriate. Imagine a city in which there are no infected people, but if people infected by the virus move in, then that must be one reason why the virus would be present in that city. Therefore, based on the idea of ^[10], the following model developed:

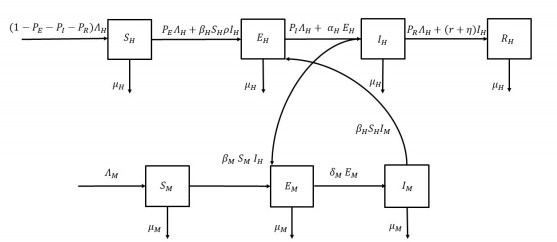
where $\Lambda_{H}$ denotes the recruitment of humans, which also means the rate at the new individuals enter human population. Of these new individuals, we hypothesize that a fraction of $1-P_{E}-P_{I}-P_{R}$ are susceptibles, $P_{E}$ are exposed, $P_{I}$ are infected and $P_{R}$ are are recovered. $\Lambda_{M}$ represents susceptible mosquitoes recruitment, $\beta_{H}$ signifies the direct transmission rate of the disease from infectious mosquitoes to susceptible humans, $\beta_{M}$ denotes the rate of transmission from infected humans to susceptible mosquitoes, $\beta_{H}\rho$ represents the rate of transmission from infected humans to susceptible humans, $\alpha_{H}$ stands for the rate of exposed humans moving into infectious class, $\delta_{M}$ is the rate flow from $E_{M}$ to $I_{M}$. Natural mortality levels associated with each subpopulation of humans and mosquitoes are denoted by $\mu_{H}$ and $\mu_{M}$, respectively, $r$ is the natural recovery rate, and $\eta$ denotes the treatment rate. All the parameters here are positive. Figure 1 shows the compartment model, which clearly shows the construction process of the model. Table 1 defines all the parameters of the model.

Theorem 1. Set initial value$F(0)\geq 0$, where

Then, the solutions of $F(t)$ at $t > 0$ are non-negative and $\lim\limits_{t\to\infty}sup N_{H}(t)\leq \frac{\Lambda_{H}}{\mu_{H}}$, $\lim\limits_{t\to\infty}sup N_{M}(t)\leq \frac{\Lambda_{M}}{\mu_{M}}$.

Proof. Total population $N_{H} = S_{H}+E_{H}+I_{H}+R_{H}$, and

Therefore, when $t\to\infty$, $0\leq N_{H}(t)\leq\frac{\Lambda_{H}}{\mu_{H}}$ holds.

The total mosquito population is expressed as $N_{M} = S_{M}+E_{M}+I_{M}$, and

Then when $t\to\infty$, $0\leq N_{M}(t)\leq\frac{\Lambda_{M}}{\mu_{M}}$ holds. Hence we have,

$\lim\limits_{t\to\infty}sup N_{H}(t)\leq \frac{\Lambda_{H}}{\mu_{H}}$, $\lim\limits_{t\to\infty}sup N_{M}(t)\leq \frac{\Lambda_{M}}{\mu_{M}}$.

Furthermore, let

We can get that $\Omega$ is the positive invariant set of the system (2.1). □

3.   Equilibria of the model and stability analysis

3.1.   The disease-free equilibrium and the basic reproduction number

When $P_{E} = 0, P_{I} = 0$, that means that no infected or exposed person moves in, the model can be written as

The disease-free equilibrium point of system (3.1) is $E_{0} = (\frac{(1-P_{R})\Lambda_{H}}{\mu_{H}}, 0, 0, \frac{P_{R}\Lambda_{H}}{\mu_{H}}, \frac{\Lambda_{M}}{\mu_{M}}, 0, 0)$. By the next generation operator method, $F$ and $V$ are respectively

The basic reproduction number can be obtained by $\rho (FV^{-1})$, that is $R_{0} = R_{1}+\sqrt{R^{2}_{1}+R_{2}}$, where

Lemma 1. For $2 R_{1}+R_{2} < 1$ if and only if $R_{0} < 1$ holds.

Proof. Because of $R_{0} = R_{1}+\sqrt{R^{2}_{1}+R_{2}}$, if $R_{0} < 1$, get $\sqrt{R_{1}^{2}+R_{2}} < 1-R_{1}$, square both sides get $2 R_{1}+R_{2} < 1$. If $2 R_{1}+R_{2} < 1$, get $R_{2} < 1-2 R_{1}$, add $R^{2}_{1}$ to both sides so $R_{1}^{2}+R_{2} < 1-2R_{1}+R_{1}^{2}$, take the square root of both sides and get $R_{1}+\sqrt{R_{1}^{2}+R_{2}} < 1$. Therefore $R_{0} < 1$ is true when $2 R_{1}+R_{2} < 1$ is true. □

3.2.   The stability of the disease-free equilibrium

The Jacobi matrix of system (3.1) at $E_{0}$ is

The Jacobi matrix shows that the three eigenvalues are $-\mu_{H}, -\mu_{H}, -\mu_{M}$. The remaining four eigenvalues can be determined by the following characteristic equation

where

From Lemma 1, we know that $2 R_{1}+R_{2} < 1$ if and only if $R_{0} < 1$ holds. Therefore all the order principal minor determinants are positive, when $K_{i}, i = 1, 2, 3, 4$. Thus, when $R_{0} < 1$, according to Hurwitz's criterion, system (3.1) is locally asymptotically stable at the equilibrium point $E_{0}$; otherwise, it is unstable. Next we give the global asymption stability of DFE.

Theorem 2. The disease-free equilibrium point $E_{0}$ of system (3.1) is globally asymptotically stable if $R_{0} < 1$; otherwise, it is unstable.

Proof. Define the Lyapunov function

The time derivative of the Lyapunov function is

The disease-free equilibrium point of system (3.1) is $E_{0}$, therefore $S_{H}^{*} = \frac{(1-P_{R})\Lambda_{H}}{\mu_{H}}, S_{M}^{*} = \frac{\Lambda_{M}}{\mu_{M}}$.

Selection constant

We get

Thus, $\frac{dV(t)}{dt}$ is negative when $R_{0} < 1$, and $\frac{dV(t)}{dt}$ is zero if and only if $S_{H} = \frac{(1-P_{R})\Lambda_{H}}{\mu_{H}}, E_{H} = I_{H} = E_{M} = I_{M} = 0, S_{M} = \frac{\Lambda_{M}}{\mu_{M}}$. Therefore the largest compact invariant set in $\Omega$ is the singleton set $E_{0}$. According to LaSalle's invariance principle ^[20], the disease-free equilibrium point $E_{0}$ of system (3.1) is globally asymptotically stable if $R_{0} < 1$; otherwise, it is unstable. □

3.3.   The existence of the endemic equilibrium

Obviously, when $P_{E}\neq 0, P_{I}\neq 0$, there is no disease-free equilibrium. Let each equation of system (2.1) equal to 0, we can get

Let the endemic equilibrium of system (3.2) be $E_{1} = (S_{H1}, E_{H1}, I_{H1}, R_{H1}, S_{M1}, E_{M1}, I_{M1})$. Denoting $k_{1} = \mu_{H}+\alpha_{H}, k_{2} = \mu_{H}+r+\eta, k_{3} = \mu_{M}+\delta_{M}$, then we have

It can be derived from Eq (3.3) that

According to Eqs (3.4) and (3.5), we assume that

According to Eq (3.8), the positive root of $f(I_{H}) = 0$ is the key to the existence of the endemic equilibrium in system (2.1). From Eqs (3.6) and (3.7), it can be determined that, when $f(I_{H}) = 0$, the positive root is in the interval $(0, I_{1})$, where

The derivatives of Eqs (3.6) and (3.7) are taken as follows

Continue with the second order derivative as follows

Because of $f^{''}_{2}(I_{H}) < 0$, $f^{''}_{1}(I_{H}) > 0$, $f^{''}(I_{H}) > 0$ holds. That admits that $f^{'}(I_{H})$ increases monotonically as $I_H$ falling in $(0, I_{1})$. Let $I_{H} = 0$, then

Therefore,

Case 1. If $f^{'}(0)\geq 0$, then $f^{'}(I_{H})\geq 0$, $I_{H} \in\left(0, I_{1}\right)$. Hence, $f(I_{H})$ is monotonically increasing as $I_{H} \in\left(0, I_{1}\right)$. Combined with $f(0) < 0$ and $f(I_{1})\rightarrow +\infty$, there is a unique $I^{*}_{H} \in\left(0, I_{1}\right)$ that satisfies $f(I_{H}) = 0$.

Case 2. If $f^{'}(0) < 0$, because $f^{'}(I_{1})\rightarrow +\infty$, then there is one $I_{2} \in\left(0, I_{1}\right)$, so that $f^{'}(I_{2}) = 0$. This proves that $f^{'}(I_{H}) < 0$ as $I_{H} \in\left(0, I_{2}\right)$ and $f^{'}(I_{H}) > 0$ as $I_{H}\in (I_{2}, I_{1})$. Noting that $f(I_{2}) < 0$ and $f(I_{1})\rightarrow +\infty$, there is a unique $I^{*}_{H} \in\left(I_{2}, I_{1}\right)$ satisfies $f(I^{*}_{H}) = 0$.

Then the following theorem holds:

Theorem 3. For system (2.1):

I) If $P_{E}, P_{I} > 0$, the system has a unique endemic equilibrium point.

II) If $P_{E}, P_{I} = 0, R_{0} > 1$, the system has a unique endemic equilibrium point ^[15].

3.4.   The stability of the endemic equilibrium

In order to simplify the system, system (2.1) can be written as the following equivalent system

Theorem 4. For system (3.9):

I) If $P_{E}, P_{I} > 0$, the only endemic equilibrium of the system is globally asymptotically stable.

II) If $P_{E}, P_{I} = 0, R_{0} > 1$, the only endemic equilibrium of the system is globally asymptotically stable.

Proof. For conclusion Ⅱ), Theorem 5.2 in Reference ^[15] has been proved, now we only prove conclusion Ⅰ).

Define the Lyapunov function as

where $\phi:(0, \infty) \rightarrow \mid R \mid, \phi(x) = x-1-\ln x$. Obviously $\phi(x)$ has a minimum $\phi(1) = 0$.

The total derivative of the Lyapunov function with respect to the system (3.9) is

Calculated separately, we can get

According to Eqs (3.13)–(3.18)

Therefore, the maximum invariant set of system (3.9) is a single point set $\{E^{*}\}$. According to LaSalle's invariance principle ^[20], the endemic equilibrium $E^{*}$ of system (3.9) is globally asymptotically stable, as is the system (2.1). □

3.5.   Numerical simulation

To verify the above theoretical results, we conducted numerical simulations using the data from ^[19], where $\Lambda_{H} = 0.4$, $P_{R} = 0.1$, $\beta_{H} = 0.0002$, $\rho = 0.0029$, $\mu_{H} = 0.1$, $\alpha_{H} = 0.0022$, $r = 0.0614799$, $\eta = 0.4$, $\Lambda_{M} = 1.3$, $\beta_{M} = 0.0009$, $\mu_{M} = 0.002$, $\delta_{M} = 0.3$.

Example 1. Set $P_{E} = 0$ $P_{I} = 0$ and $\eta = 0.4$, then $R = 0.8946 < 1$. According to Theroem 2, the disease-free equilibrium point in model (3.1) is globally asymptotically stable. From Figure 2, it can be seen that both $I_{h}$ and $I_{m}$ eventually converge to 0, although the initial values have different starting points.

Example 2. When $P_{E} = 0.15$ $P_{I} = 0.25$, it follows from Theorems 3 and 4 that the endemic equilibrium point is globally asymptotically stable (see Figure 3).

4.   Optimal control analysis and numerical simulation

4.1.   Optimal control analysis

Optimal control theory is used to determine the method to achieve the minimum cost and maximum performance under various assumptions ^[21,22]. In this section, to reduce infection vectors and control the spread of diseases, based on the previous analysis and combined with reality, several control strategies were proposed.

The two most common ways to control Zika virus are the efforts on preventing Zika infections (e.g. using mosquito nets, condoms, and so on) and the efforts on eliminating mosquitoes by insecticides. For the risk of someone carrying the virus in the immigrant population, we propose a measure of virus screening.

It is important to note that the control variables are primarily acting on the parameters corresponding to each control measure. For example, measures to prevent mosquito bites will change the rate of mosquito bite infection, so the reduction in infection rate is expressed in the form $(1-u_{1}) \beta_{H}, (1-u_{1}) \beta_{M}$. Similarly, if a mosquito killer is to be used, then it is to some extent increasing the mortality rate of mosquitoes, so expressed in the form $(1+u_{3}) \mu_{M}$. The implementation of virus screening will reduce the proportion of exposure and infection in the immigrant population. So, we denote it by the form $(1-u_{2}) P_{E}, (1-u_{2}) P_{I}$. Therefore, our optimal control model is given by

where $u_{1}$, $u_{2}$, $u_{3}$ are described in Table 2.

In general, if the basic reproduction number exists, the control scheme can be proposed by limiting the basic reproduction number to less than 1 and backtracking the values of the control parameters. However, in this model, if $P_{I}\neq 0, P_{E}\neq 0$, there is no the basic reproduction number, so the above method cannot be used to study the control measures. Therefore, in this paper, the transmission model is first qualitatively analyzed to reveal the dynamics behavior of continuous virus transmission. Then, the Pontryagin maximum principle ^[23] will be used to find the optimal control scheme to achieve virus control in a limited time.

The objective function is defined as follows

where $\omega_{E_{H}}, \omega_{I_{H}}, \omega_{E_{M}}, \omega_{I_{M}}, a_{1}, a_{2}, a_{3}$ represents the weight coefficients of the control variables, which are designed to maintain a balance among the items of the integration function so that no dominant individual term emerges. $t_{f}$ is the terminal moment when the control policy is implemented. Our goal is to find a set of control parameters $(u^{*}_{1}, u^{*}_{2}, u^{*}_{3})$ satisfying

Control constraint set is $U = \left\{\left(u_{1}, u_{2}, u_{3}\right) \mid 0 < u_{1}, u_{2}, u_{3} < 1\right\}$. It should be noticed that the right side of model (4.2) is bounded and the objective function is convex. A sufficient condition for the existence of optimal control indicates that the model has optimal control. The Lagrange function is

Define the Hamilitonian function as

From Pontryagin extreme value principle, the control set $u(t)$ should satisfy the following necessary conditions:

Theorem 5. There is a set of $u_{1}, u_{2}, u_{3}$, so that $J\left(u_{1}^{*}, u_{2}^{*}, u_{3}^{*}\right) = \min J\left(u_{1}, u_{2}, u_{3}\right)$. The optimal control expressions are as follows

Proof. From the extremum condition of the control equation, we have $\frac{\partial H}{\partial u_{1}} = 0, \frac{\partial H}{\partial u_{2}} = 0, \frac{\partial H}{\partial u_{3}} = 0$, where

Then, we can obtain the solution of the equations as follows

Therefore, the optimal control solution can be expressed as

□

4.2.   Numerical simulation

4.2.1.   The fitting of parameters

Since the duration of Zika virus infection is about one week, we assumed a natural recovery rate of 0.862 per week in humans. Then, based on the weekly infection data of the Brazilian Zika virus in the first 20 weeks of 2015 in Reference ^[25], we used the least square method to fit the remaining parameters on the DEDiscover software, and the fitting results are shown in Table 3 and Figure 4. The sum of squares of the fitting residuals is 0.116.

4.2.2.   Optimal control results

In order to find out the optimal control, we used the forward-backward Runge-Kutta method ^[26] to solve the optimal solution. Select the balance weight coefficient as $\omega_{E_{H}} = 50, \omega_{I_{H}} = 30, \omega_{E_{M}} = 0.2, \omega_{I_{M}} = 0.1, a_{1} = 30, a_{2} = 20, a_{3} = 50$.

The results showed that the number of exposed people, infected people, exposed mosquitoes and infected mosquitoes were all on the rise before the control. Among them, the number of infected mosquitoes even reached a peak of 30,000 before the control, and the number of infected people was as high as 15,000 before the control. However, the number of infected and exposed mosquitoes and people decreased significantly under the control measures $u_{1}$, $u_{2}$, and $u_{3}$. After control, the number of infected and exposed people tended to zero (see Figure 5(b), (d)) and the number of infected mosquitoes stabilized below 20 (see Figure 5(f), (h)). The spread of Zika virus was well controlled. Figure 6 shows the time-varying control profile.

5.   Cost-effectiveness analysis

Next, we analyze the cost-effectiveness of investments in Zika virus prevention and control. Assume that the percentage of testing is the number of existing infections as a percentage of the immigrating population. The total cases averted (TCA) though control and the total costs (TC) associated with intervention are given by the following formula

where the factors show the per capita cost of the control strategy. According to estimates from the Global Vector Control Response 2017–2030 (GVCR; WHO ^[27]), the annual per person cost of insecticides is approximately $4.24$ dollars and the per person annual cost of mosquito nets is $1.27$ dollars. Assuming that each person in transit is tested only once per week, the cost of testing and screening is estimated to be $10.3$ dollars per person per week based on online quotes for commercially available Zika virus test reagents. Based on the data simulation results, we can eliminate the virus by using $u_{1}$ and $u_{3}$. If only $u_{3}$ works, the number of patients will reduce, but the virus will not disappear. Using only u1 will not meet the purpose of control. Therefore, based on the available strategies, we compare the following 3 control options:

Control option 1. Using mosquito nets and spraying insecticides: $u_{1} \neq 0, u_{2} = 0, u_{3} \neq 0$.

Control option 2. Using mosquito nets and test screening: $u_{1} \neq 0, u_{2} \neq 0, u_{3} = 0$.

Control option 3. Using mosquito nets, screening tests, spraying insecticides: $u_{1} \neq 0, u_{2} \neq 0, u_{3} \neq 0$.

Here, incremental cost-benefit ratio (ICER) is used to analyze the cost-effectiveness results of the three schemes. The formula is as follows

ICER represents the incremental cost per unit of incremental health outcome, which is a classic method to analyze cost-effectiveness ^[26]. It can be seen from Table 4 that the ICER value of control option 2 is 326.0178819117, which is significantly higher than that of options 1 and 3. Therefore, control option 2 requires higher cost and lower efficiency, so option 2 is excluded from the alternative plan. Comparing options 1 and 3, you will find the ICER value of option 1 is higher than that of option 3. Therefore, it can be concluded that option 3 has the lowest ICER value, so it is the lowest cost and the highest efficiency option. From Figure 7, it is clear that option 3 can achieve the effect of option 1. From the perspective of environmental sustainability, option 3 is less harmful to the environment and human beings.

6.   Conclusions

This paper focuses on the optimal control and cost-effective analysis of the Zika virus model with migration. Non-negativity and boundedness of the model are also shown. When no infected population enters, a disease-free equilibrium point exists in the system, and the disease-free equilibrium point was globally asymptotically stable. When cases migrate, there is no disease-free equilibrium in the model, only an epidemic equilibrium with global asymptotic stability. Based on this model, we propose three control measures $u_{1}$, which means reducing mosquito bites through mosquito nets, and mosquito repellants. The factor $u_{2}$ stands for reducing the likelihood of infection and exposure among immigrants through testing and screening immigrants. The parameter $u_{3}$ represents the reduction of the mosquito population by spraying insecticides to prevent the spread of the Zika virus. The necessary conditions for the existence of an optimal solution are given using Pontriagin's maximum principle. Based on Control option 1, the cost-effectiveness of three control strategies was compared and analyzed. According to the incremental cost-effectiveness ratio results (see Table 3), the ICER value of Control option 2 is 326.0178819117, which is much higher than options 1 and 3. This means that Control option 2 is the least efficient and most expensive. On the other hand, Control option 3 with the lowest ICER value of -64.3479200904 exhibits the lowest cost and the highest return. Especially from the perspective of human health and environmental protection, the combination of these three options is capable of reducing our dependence on pesticides. Indeed, although we are concerned with screening, if immunization against the Zika virus is possible and the immigrant population is fully vaccinated and protected, this factor could also be reflected in the control item. Therefore, both vaccination and screening are indispensable control measures to control the Zika virus.

In Zika virus transmission, the environment also has an impact on the transmission of the virus, such as temperature, humidity, etc. Subsequently, there will be corresponding measures adjusted in virus control, which will be considered in the next study.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors acknowledge the useful suggestions and thoughtful comments made by the referees on their earlier version of this work.

The work is supported by Shaanxi Provincial Natural Science Foundation Project (2023-JC-YB-084).

Conflict of interest

The authors declare that they have no competing interests.