In the present work, we consider a one-dimensional Bresse-Timoshenko system with neutral delay term and a viscous damping acting on vertical displacement of the beam. Under appropriate assumptions on the kernel of this kind of delay and based on the multipliers method, we construct a suitable Lyapunov functional that allows us to establish an exponential decay of the energy in spite of the existence of the delay. Moreover, our result does not depend on any condition on the coefficients of the system. Finally, we present some numerical results to illustrate the theoretical result obtained.
Citation: Houssem Eddine Khochemane, Ali Rezaiguia, Hasan Nihal Zaidi. Exponential stability and numerical simulation of a Bresse-Timoshenko system subject to a neutral delay[J]. AIMS Mathematics, 2023, 8(9): 20361-20379. doi: 10.3934/math.20231038
| [1] | Li Wan, Qinghua Zhou, Hongbo Fu, Qunjiao Zhang . Exponential stability of Hopfield neural networks of neutral type with multiple time-varying delays. AIMS Mathematics, 2021, 6(8): 8030-8043. doi: 10.3934/math.2021466 |
| [2] | Khaled zennir, Djamel Ouchenane, Abdelbaki Choucha, Mohamad Biomy . Well-posedness and stability for Bresse-Timoshenko type systems with thermodiffusion effects and nonlinear damping. AIMS Mathematics, 2021, 6(3): 2704-2721. doi: 10.3934/math.2021164 |
| [3] | Boonyachat Meesuptong, Peerapongpat Singkibud, Pantiwa Srisilp, Kanit Mukdasai . New delay-range-dependent exponential stability criterion and $ H_\infty $ performance for neutral-type nonlinear system with mixed time-varying delays. AIMS Mathematics, 2023, 8(1): 691-712. doi: 10.3934/math.2023033 |
| [4] | Yijia Zhang, Tao Xie, Yunlong Ma . Robustness analysis of exponential stability of Cohen-Grossberg neural network with neutral terms. AIMS Mathematics, 2025, 10(3): 4938-4954. doi: 10.3934/math.2025226 |
| [5] | Sheng Wang, Shaohua Long . Finite-time stability analysis of singular neutral systems with time delay. AIMS Mathematics, 2024, 9(10): 26877-26901. doi: 10.3934/math.20241308 |
| [6] | Yakufu Kasimu, Gulijiamali Maimaitiaili . Non-fragile ${H_\infty }$ filter design for uncertain neutral Markovian jump systems with time-varying delays. AIMS Mathematics, 2024, 9(6): 15559-15583. doi: 10.3934/math.2024752 |
| [7] | Xuelian Jin . Exponential stability analysis and control design for nonlinear system with time-varying delay. AIMS Mathematics, 2021, 6(1): 102-113. doi: 10.3934/math.2021008 |
| [8] | Shuo Ma, Jiangman Li, Qiang Li, Ruonan Liu . Adaptive exponential synchronization of impulsive coupled neutral stochastic neural networks with Lévy noise and probabilistic delays under non-Lipschitz conditions. AIMS Mathematics, 2024, 9(9): 24912-24933. doi: 10.3934/math.20241214 |
| [9] | Tijani A. Apalara, Aminat O. Ige, Cyril D. Enyi, Mcsylvester E. Omaba . Uniform stability result of laminated beams with thermoelasticity of type Ⅲ. AIMS Mathematics, 2023, 8(1): 1090-1101. doi: 10.3934/math.2023054 |
| [10] | Abdelbaki Choucha, Asma Alharbi, Bahri Cherif, Rashid Jan, Salah Boulaaras . Decay rate of the solutions to the Bresse-Cattaneo system with distributed delay. AIMS Mathematics, 2023, 8(8): 17890-17913. doi: 10.3934/math.2023911 |
In the present work, we consider a one-dimensional Bresse-Timoshenko system with neutral delay term and a viscous damping acting on vertical displacement of the beam. Under appropriate assumptions on the kernel of this kind of delay and based on the multipliers method, we construct a suitable Lyapunov functional that allows us to establish an exponential decay of the energy in spite of the existence of the delay. Moreover, our result does not depend on any condition on the coefficients of the system. Finally, we present some numerical results to illustrate the theoretical result obtained.
Throughout the years, many works have dealt with beam theories due to their important applications in high technology of flexible structures. Historically, it is well known that one of the oldest beam theories is the Euler-Bernoulli beam theory, which is a simplification of linear isotropic beams. It was first enunciated circa 1750, but it was not applied on a large scale until the development of the Eiffel Tower and the Ferris Wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution. Later on, other beam theories appeared and were considered as improvements of the Euler-Bernoulli theory, such as the Rayleigh beam theory [28] and the Timoshenko beam theory [31]. In [13,14,15], Elishakoff et al. gave a brief description of the beam model in the one-dimensional case for beam vibrations. The classical Euler-Bernoulli differential equation for free vibration of uniform beams is given by
| EIφxxxx+ρAφtt=0, | (1.1) |
where φ(x,t) is the beam deflection from its equilibrium position, E is the modulus of elasticity, I is the moment of inertia of the cross section, ρ is the material density of the beam material, A is the cross-sectional area, x is the axial coordinate, and t is the time. Later, Rayleigh [28] proposed a correction to the Euler-Bernoulli equation (1.1), by taking into account the rotary movements of the beam elements in addition to the translatory ones. From a mathematical modeling point of view for vibrating beams, it is instructive to re-derive briefly this equation. The angle of rotation equals the slope of the deflection curve φx, and the corresponding angular acceleration is given by φxtt. As a consequence, the moment of inertia of the element about an axis through its center of mass equals ρIφxtt. By exploiting this moment and taking into account d'Alembert's principle for dynamic equilibrium [22], we obtain
| V−Mx+ρIφxtt=0, | (1.2) |
where V(x,t) is the shearing force, and M(x,t) is the bending moment. Replacing V from Eq (1.2) in the case of dynamic equilibrium condition for forces in the φ-direction of the transverse vibration, we have
| Vx=−ρAφtt=(Mx−ρIφxtt)x. |
Physically and from elastic theory, the bending moment M coincides with EIφxx, which leads to the final governing equation obtained in the Rayleigh model for the uniform beam oscillations,
| EIφxxxx+ρAφtt−ρIφxxtt=0, | (1.3) |
which is known as the rotatory inertial equation.
Afterwards, Timoshenko [31] extended Eq (1.3) by incorporating the impact of the shear deformation. In another term, he expressed the slope of the deflection curve in two parts,
| φx=−ψ+β, | (1.4) |
with ψ as the rotation of the cross-sections with the neglect of the shear deformation and β as the angle associated with the shear deformation at the neutral axis in the same cross-section. On the other hand, according to the mechanics of solids we can write
| M=EIψx, | (1.5) |
| V=k1βAG=k1AG(φx+ψ), | (1.6) |
where k1 is the shear coefficient, and G is the shear modulus. The state of dynamic equilibrium of forces in the vertical direction is given by
| ρAφtt−Vx=0. | (1.7) |
Deriving with respect to t Eq (1.4) and substituting it in the dynamic equilibrium equation of motion (1.2), we get
| V−Mx+ρIψtt=0. | (1.8) |
The Timoshenko system was obtained by substituting, respectively, (1.6) and (1.5) into (1.7) and (1.8), thus:
| {−k1AG(φx+ψ)x+ρAφtt=0,k1AG(φx+ψ)−EIψxx+ρIψtt=0, |
where ρ1=ρA represents the mass density, ρ2=ρI is the moment mass inertia, b=EI is the rigidity coefficient (of the cross-section), and k=k1AG is the shear modulus of elasticity. Then, the Timoshenko system takes the following form:
| {ρ1φtt−k(φx+ψ)x=0,ρ2ψtt−bψxx+k(φx+ψ)=0. |
It should be noted that the mentioned problem plays a crucial role in engineering applications, and for more details on the valuable resources that have been realized regarding the Timoshenko system, we refer the readers to [5,6,7,8,9,31].
For the physical and technical reasons mentioned in [13], Elishakoff proposed a combination of Eq (1.2) which comes from d'Alembert's principle with Eq (1.7) from the Timoshenko hypothesis, resulting in the following coupled system:
| {ρ1φtt−k(φx+ψ)x=0,−ρ2φttx−bψxx+k(φx+ψ)=0. |
Many investigations have been realized concerning the asymptotic behavior of the solution of the Bresse-Timoshenko system. Among them, we cite the works [18,19,34], in which the authors established different types of stability results such as exponential and general decay based on many dissipation terms.
There are also other investigations concerning the delay which appear in many models of mathematics that come from engineering biological science, economics, physiology and epidemiology. Delay effects arise in many applications depending not only on the present state but also on some past occurrences, and they have attracted a lot of attention from researchers in diverse fields of human endeavors, such as mathematics, engineering, science and economics. The presence of delay may be a source of instability of systems which are uniformly asymptotically stable in the absence of delay unless additional control terms have been used (see [10,11,17,25,26,33]). Also, the introducing of this complementary may lead to ill-posedness, as shown in many works such as [11,27] and the references therein. On the other hand, the delay has an important role in the control of PDEs, and this has appeared in a lot of studies (see [1,2,3,4,17,20,21,24,25,26,33]). In addition to the well-known discrete delays, there are several others. We are interested here in the neutral delay, where the delay is occurring in the second (highest) derivative. For more details, see previous studies ([12,13,14,15,16,23,32]) and the references therein.
Among the investigations that have been realized concerning the asymptotic behavior with neutral delay, we cite the work of Tatar [30] where he considered the wave equation with neutral delay, and he showed that the solution decays in an exponential manner under some conditions on the kernel of distributed neutral delay.
In [29], Seghour et al. studied the following thermoelastic laminated system with neutral delay:
| {ρwtt+G(ψ−wx)x+Awt=0,x∈(0,1),t>0,Iρ(3stt−ψtt)−G(ψ−wx)−(3s−ψ)+μθx=0,x∈(0,1),t>0,3Iρ(st+∫t0h(t−r)st(r)dr)t+3G(ψ−wx)+4γs−3sxx=0,x∈(0,1),t>0,θt−κθxx+μ(3s−ψ)tx=0,x∈(0,1),t>0, |
with boundary conditions
| {ψ(0,t)=s(0,t)=θx(0,t)=wx(0,t)=0,t≥0,θ(1,t)=w(1,t)=sx(1,t)=ψx(1,t)=0,t≥0, |
and initial data
| {(w,ψ,s,θ)(x,0)=(w0,ψ0,s0,θ0),x∈(0,1),(wt,ψt,st)(x,0)=(w1,ψ1,s1),x∈(0,1). |
They showed that the dissipation given by the combination of heat effect and the frictional damping stabilize exponentially the system in the case of equal speeds of wave propagation even if the delays, in general, are of a destructive nature. In the case of non-equal wave speeds and with an additional assumption on the kernel, they proved a polynomial stability.
Motivated by the previous works, in this paper we consider the following Bresse-Timoshenko system subject to a neutral delay:
| {ρ1(φt+∫t0h(t−s)φt(s)ds)t=k(φx+ψ)x−μ1φt, −ρ2φttx=bψxx−k(φx+ψ),in (0,1)×(0,+∞),in (0,1)×(0,+∞), | (1.9) |
with the initial and boundary conditions
| {φ(x,0)=φ0(x), φt(x,0)=φ1(x), ψ(x,0)=ψ0(x), ψt(x,0)=ψ1(x),φ(0,t)=φ(1,t)=ψ(0,t)=ψ(1,t)=0, x∈(0,1),x∈(0,1),t∈(0,+∞). | (1.10) |
First, we give an existence and uniqueness result of the solution using the Faedo-Galerkin method. Then, based on the energy method and by constructing a suitable Lyapunov functional using the multipliers method as well as under an appropriate assumptions on the kernel of the neutral delay term, we prove that the system is exponentially stable in spite of the existence of the neutral delay irrespective of any stability number. In the absence of neutral delay, there is a similarity with the previous works like [18,19,34] concerning the estimation of the energy terms. In our case and compared to the work of Seghour et al. in [29], we were able to dispense the thermal effect depending on the viscous damping acting on vertical displacement of the beam to control the neutral delay term and to guarantee an exponential stability of the solution irrespective of wave speeds or any other relationship between the system parameters. In other words, the unique dissipation given only by the viscous damping is strong enough to provoke an exponential stability and control the neutral delay. Finally, we present some numerical results using MATLAB software to validate the theoretical result obtained by carrying out a discretization using the classical finite difference method for the spatial and temporal discretization.
This paper is organized as follows: In Section 2, we introduce some assumptions needed in the next sections to prove the main result, and we give a result concerning the well-posedness of problem (1.9)–(1.10). In Section 3, we prove the energy decay of the system. In Section 4, we use the energy method to prove the exponential decay result. In Section 5, some numerical simulations are presented.
In this section we present our assumptions on both kernels and introduce the energy functional and another functional.
We use the standard Lebesgue space L2(0,1) and the Sobolev space H10(0,1) with their usual scalar products and norms. Also, in what follows we will use the following notations:
| (h∘Ψ)(t)=∫t0h(t−s)(∫10(Ψ(t)−Ψ(s))2dx)ds, t≥0, |
and
| (h∗Ψ)(t)=∫10∫t0h(t−s)Ψ(s)2dsdx, t≥0. |
To achieve our goal, we need to introduce the following hypothesis and assumptions:
(H1) The kernel h is a nonnegative continuously differentiable and summable function satisfying
| −μh(t)≤h′(t)≤0,∀t≥0, where μ>0,ˉh=∫∞0h(s)ds<1. |
(H2) exp(ςt)h(t)∈L1(R+) for some ς>0.
Note that if ∫+∞0eςsh(s)ds<∞, and limt⟶∞exp(ςt)h(t)<∞, then
| ∫+∞0eςs|h′(s)|ds=−∫+∞0eςsh′(s)ds=−eςsh(s)∣∞0+ς∫+∞0eςsh(s)ds<∞. |
To simplify the calculations, we are obligated to announce this lemma which is usable in the following sections.
Lemma 1 ([29]). For any function Ψ∈C1([0,∞);L2(0,1)) and any h∈C1([0,∞)), we have the following identity:
| ∫10Ψ(t)(∫t0h(t−s)Ψt(s)ds)dx=−12(h′∘Ψ)(t)+12ddt∫10(∫t0h(t−s)Ψ2(s)ds)dx+h(t)2∫10Ψ2dx−h(t)∫10Ψ(0)Ψ(t)dx. |
For completeness, we state without proof the following global existence and regularity result which can be proved by using the standard Faedo-Galerkin method, for which we refer the reader to [24].
Theorem 1. Let (φ0,φ1)∈H10(0,1)×L2(0,1) and (ψ0,ψ1)∈H10(0,1)×L2(0,1) be given. Assume that (H1)–(H2) are satisfied, and then the problem (1.9)–(1.10) has a unique global (weak) solution satisfying
| φ,ψ∈C(R+,H10(0,1))∩C1(R+,L2(0,1)). |
In this section, we use the energy method to study the asymptotic behavior of solutions of the system (1.9)–(1.10). First, we state and prove the following lemma.
Lemma 2. Let (φ,ψ) be a solution of system (1.9)–(1.10). Then, the energy associated to the system (1.9)–(1.10) is defined by
| E(t)=12∫10(ρ1φ2t +k(φx+ψ)2+ρ2φ2tx+bψ2x+ρ1ρ2kφ2tt)dx+ρ1(h∗φt)(t)+ρ1ρ2k(h∗φtt)(t), | (3.1) |
satisfying
| ddtE(t)≤ρ12(h′∘φt)(t)−μ1ρ2k∫10φ2ttdx+ρ1ρ2k(h′∘φtt)(t)−μ1∫10φ2t dx+ζh(t),ζ>0. | (3.2) |
Proof. Multiplying (1.9)1 and (1.9)2, respectively, by φt and ψt and integrating by parts, we get
| {ρ12ddt∫10φ2t dx+ρ1∫10φt(∫t0h(t−s)φt(s)ds)t dx=−k∫10(φx+ψ)φtx dx−μ1∫10 φ2tdx,ρ2∫10φttψxtdx+b2ddt∫10ψ2xdx=−k∫10(φx+ψ)ψtdx. | (3.3) |
Taking the derivative of (1.9)1 with respect to t, we obtain
| ψtx=ρ1kφttt−φtxx+ρ1k(∫t0h(t−s)φt(s)ds)tt+μ1kφtt, |
noting that
| (∫t0h(t−s)φt(s)ds)tt=(∫t0h(t−s)φtt(s)ds+h(t)φt(0))t=∫t0h(t−s)φttt(s)ds+h(t)φtt(0)+h′(t)φt(0). |
So,
| ψtx=ρ1kφttt−φtxx+ρ1k∫t0h(t−s)φttt(s)ds+ρ1kh(t)φtt(0)+ρ1kh′(t)φt(0)+μ1kφtt. | (3.4) |
Substituting (3.4) in (3.3)2, the system (3.3) becomes
| {ρ12ddt∫10φ2t dx+ρ1∫10φt(∫t0h(t−s)φt(s)ds)t dx=−k∫10(φx+ψ)φtxdx−μ1∫10 φ2tdx,ρ1ρ22kddt∫10φ2ttdx+ρ22ddt∫10φ2txdx+ρ1ρ2k∫10φtt(∫t0h(t−s)φttt(s)ds)dx+ρ1ρ2kh(t)∫10φttφtt(0)dx+ρ1ρ2kh′(t)∫10φttφt(0)dx+b2ddt∫10ψ2xdx=−μ1ρ2k∫10φ2ttdx−k∫10(φx+ψ)ψtdx. | (3.5) |
On the other hand, by applying Lemma 1, we have
| ρ1∫10(∫t0h(t−s)φt(s)ds)tφt dx=ρ1h(t)∫10φtφt(0)dx+ρ1∫10φt(∫t0h(t−s)φtt(s)ds) dx=ρ1h(t)∫10φtφt(0)dx−ρ12(h′∘φt)(t)+ρ12ddt∫10(∫t0h(t−s)φ2t(s)ds)dx+ρ12h(t)∫10φ2t dx−ρ1h(t)∫10φtφt(0)dx, |
and
| ρ1ρ2k∫10φtt(∫t0h(t−s)φttt(s)ds)dx=ρ1ρ22kddt∫10(∫t0h(t−s)φ2tt(s)ds)dx−ρ1ρ2kh(t)∫10φttφtt(0)dx+ρ1ρ2kh(t)∫10φ2ttdx−ρ1ρ2k(h′∘φtt)(t). |
Therefore, the system (3.5) is equivalent to
| d2dt∫10(ρ1φ2t +k(φx+ψ)2+ρ2φ2tx+bψ2x+ρ1ρ2kφ2tt+ρ1∫t0h(t−s)φ2t(s)ds+ρ1ρ2k∫t0h(t−s)φ2tt(s)ds)dx=ρ12(h′∘φt)(t)−ρ1ρ2k(1+h(t)2)∫10φ2ttdx+ρ1ρ2k(h′∘φtt)(t)−(ρ12h(t)+μ1)∫10φ2t dx−ρ1ρ2kh(t)∫10φttφt(0)dx. |
By using Young's inequality and the hypothesis (H1), we obtain
| −ρ1ρ22h′(t)∫10φttφt(0)dx=ρ1ρ22μh(t)∫101√kφtt√kφt(0)dx≤ρ1ρ22kμh(t)δ1∫10φ2ttdx+ρ1ρ22δ1μh(t)k∫10φ2t(0)dx, |
and taking δ1=12μ
| −ρ1ρ22h′(t)∫10φttφt(0)dx≤ρ1ρ24kh(t)∫10φ2ttdx+ρ1ρ24μ2h(t)k∫10φ2t(0)dx. |
Then,
| ddtE(t)≤ρ12(h′∘φt)(t)−ρ1ρ2k∫10φ2ttdx+ρ1ρ2k(h′∘φtt)(t)−μ1∫10φ2t dx+ζh(t), |
where ζ=ρ1ρ24μ2k∫10φ2t(0)dx.
In this section, we establish an exponential decay result of solutions for the considered problem. For that, we need the following lemmas to achieve our goal.
Lemma 3. Let (φ,ψ) be the solution of (1.9)–(1.10). Then, the functional
| F1(t)=−ρ1∫10φt(φt+∫t0h(t−s)φt(s)ds)dx−k∫10φtxφxdx−μ12∫10φ2tdx, |
satisfies the estimate
| F′1(t)≤−k∫10φ2txdx+((3+h(t)2)ρ1+k24ε1)∫10φ2ttdx+ε1∫10ψ2xdx+ρ12(3+h(t))∫10φ2tdx+ρ1h(t)∫10φ2t(0)dx+ρ1¯h2(h∗φt)(t)+ρ1¯h(h∗φtt)(t). |
Proof. By differentiating F1(t) with respect to t, using the first equation of (1.9) and integrating by parts, we obtain
| F′1(t)=−2ρ1∫10φttφtdx+ρ1∫10φ2ttdx−k∫10φttψxdx−k∫10φ2txdx−ρ1∫10φtt∫t0h(t−s)φt(s)dsdx−ρ1∫10φt∫t0h(t−s)φtt(s)dsdx+ρ1∫10φtt∫t0h(t−s)φtt(s)dsdx−ρ1h(t)∫10φtφt(0)dx+ρ1h(t)∫10φt(0)φttdx. | (4.1) |
By using Young's inequality, we obtain
| −2ρ1∫10φttφtdx≤ρ1∫10φ2ttdx+ρ1∫10φ2tdx, | (4.2) |
| −ρ1h(t)∫10φtφt(0)dx≤ρ12h(t)∫10φ2tdx+ρ12h(t)∫10φ2t(0)dx, | (4.3) |
| ρ1h(t)∫10φt(0)φttdx≤ρ12h(t)∫10φ2ttdx+ρ12h(t)∫10φ2t(0)dx, | (4.4) |
| −k∫10φttψxdx≤ε1∫10ψ2xdx+k24ε1∫10φ2ttdx. | (4.5) |
By using Young's and Cauchy Schwarz inequalities, we obtain
| −ρ1∫10φtt∫t0h(t−s)φt(s)dsdx≤ρ12∫10φ2ttdx+ρ1¯h2(h∗φt)(t), | (4.6a) |
| −ρ1∫10φt∫t0h(t−s)φtt(s)dsdx≤ρ12∫10φ2tdx+ρ1¯h2(h∗φtt)(t), | (4.7) |
| ρ1∫10φtt∫t0h(t−s)φtt(s)dsdx≤ρ12∫10φ2ttdx+ρ1¯h2(h∗φtt)(t). | (4.8) |
Inserting (4.2)–(4.8) in (4.1), we obtain (4.1).
Lemma 4. Let (φ,ψ) be the solution of (1.9)–(1.10). Then, the functional
| F2(t):=−ρ2∫10φtxψdx+ρ1∫10φ(φt+∫t0h(t−s)φt(s)ds)dx, | (4.9) |
satisfies the estimate
| F′2(t)≤−b∫10ψ2xdx−k∫10(φx+ψ)2dx+ρ2∫10φ2txdx+3ρ12∫10φ2tdx+ρ1¯h2(h∗φtt)(t). | (4.10) |
Proof. By differentiating F2(t) with respect to t, exploiting (1.9), integrating by parts and using the Timoshenko hypothesis (1.4), we obtain
| F′2(t)=−b∫10ψ2xdx+ρ2∫10φ2txdx−k∫10(φx+ψ)2dx+ρ1∫10φ2tdx+ρ1∫10φt∫t0h(t−s)φt(s)dsdx. |
By using Young's and Cauchy Schwarz inequalities, we have (4.10).
Lemma 5. Let (φ,ψ) be the solution of (1.9)–(1.10). Then, the functional
| F3(t):=e−ζt∫10∫t0eζs˜H1(t−s)φ2t(s)dsdx, | (4.11) |
satisfies the following estimate:
| F′3(t)=−ζF3(t)+˜H1(0)∫10φ2tdx−(h∗φt)(t), | (4.12) |
where ˜H1(t)=∫∞th(s)eζsds.
Proof. By differentiating F3(t) with respect to t,
| F′3(t)=−ζe−ζt∫10∫t0eζs˜H1(t−s)φ2t(s)dsdx+e−ζt∫10(∫t0eζs˜H1(t−s)φ2t(s)ds)tdx=−ζF3(t)+e−ζt∫10(eζt˜H1(0)φ2t−∫t0eζth(t−s)φ2t(s)ds)dx=−ζF3(t)+˜H1(0)∫10φ2tdx−(h∗φt)(t), |
which gives (4.12).
Lemma 6. Let (φ,ψ) be the solution of (1.9)–(1.10). Then, the functional
| F4(t):=e−ζt∫10∫t0eζs˜H1(t−s)φ2tt(s)dsdx | (4.13) |
satisfies the estimate
| F′4(t)≤−ζF4(t)+˜H1(0)∫10φ2ttdx−(h∗φtt)(t). | (4.14) |
Proof. By differentiating F4(t) with respect to t, as in the case of F3(t), we obtain the desired result.
Next, we define a Lyapunov function L(t) by
| L(t):=NE(t)+N1F1(t)+N2F2(t)+N3(F3(t)+F4(t)), | (4.15) |
where N, N1, N2 and N3 are positive constants that will be chosen appropriately later.
Lemma 7. Let (φ,ψ) be the solution of (1.9)–(1.10). Then, there exist two positive constants κ1 and κ2 such that the Lyapunov functional (4.15) satisfies
| κ1(E(t)+F3(t)+F4(t))≤L(t)≤κ2(E(t)+F3(t)+F4(t)),∀t≥0, | (4.16) |
and
| L′(t)≤−β1(E(t)+F3(t)+F4(t))+C2h(t),β1>0. | (4.17) |
Proof. From (4.15), we have
| |L(t)−NE(t)−N3(F3(t)+F4(t))|=N1|F1(t)|+N2|F2(t)|+N3|F3(t)+F4(t)|≤ρ1N1∫10|φt(φt+∫t0h(t−s)φt(s)ds)|dx+kN1∫10|φtxφx|dx+μ12N1∫10φ2tdx+ρ2N2∫10|φtxψ|dx+ρ1N2∫10|φ(φt+∫t0h(t−s)φt(s)ds)|dx. |
By Young's, Cauchy Schwarz and Poincaré's inequalities and with some transformations, we obtain
| |L(t)−NE(t)−N3(F3(t)+F4(t))|≤λ1E(t). |
Therefore,
| (N−λ1)E(t)+N3(F3(t)+F4(t))≤L(t)≤(N+λ1)E(t)+N3(F3(t)+F4(t)). |
By choosing N (depending on N1, N2, N3) sufficiently large, we obtain (4.16) with
| κ1=min{N−λ1,N3},κ2=max{N+λ1,N3}. |
Now, by differentiating L(t), recalling (3.2), (4.1), (4.10), (4.12) and (4.14), and setting ε1=1N1, we arrive at
| L′(t)≤−[Nμ1−N1ρ12(3+h(t))−3ρ14N2−N3˜H1(0)]∫10φ2tdx−N3˜H1(0)∫10ψ2tdx−kN2∫10(φx+ψ)2dx−(kN1−N2ρ2)∫10φ2txdx−[ρ1ρ2kN−N21k24−N3˜H1(0)]∫10φ2ttdx−(N2b−1)∫10ψ2xdx−(N3−ρ1¯h2N1)(h∗φtt)(t)−[N3−ρ1¯h2N1−ρ1¯h2N2](h∗φt)(t)+(ρ12N)(h′∘φt)(t)+(ρ1ρ2kN)(h′∘φtt)(t)−N3ζ(F3(t)+F4(t)). | (4.18) |
At this point, we need to choose our constants very carefully. First, we choose N2 large enough such that
| N2b−1>0. |
Once N2 is fixed, we take N1 large enough so that
| kN1−N2ρ2>0. |
After that, we pick N3 large enough such that
| {N3−ρ1¯h2N1−ρ1¯h2N2>0, andN3−ρ1¯h2N1>0. |
Finally, we select N large enough so that
| {Nμ1−N1ρ12(3+h(t))−3ρ14N2−N3˜H1(0)>0,andρ1ρ2kN−N21k24−N3˜H1(0)>0. |
With all these choices, we obtain (4.17).
We are now ready to state and prove the following exponential stability result.
Lemma 8. Let (φ,ψ) be a solution of (1.9)–(1.10), and assume that (H1)–(H2) hold. Then, there exist two positive constants τ1 and τ2 such that
| E(t)≤τ2e−τ1t, ∀t≥0. | (4.19) |
Proof. By using (4.17) and the right side of (4.16), we get
| L′(t)≤−C1L(t)+C2h(t), | (4.20) |
where C1=β1κ2>0.
Multiplying (4.20) by exp(C1t), we obtain
| ddt(L(t)exp(C1t))≤C2exp(C1t)h(t). | (4.21) |
Integrating over (0,T) the inequation (4.21) and choosing C1 smaller than ς, we have
| L(T)exp(C1T)≤L(0)+C2∫T0exp(ςt)h(t)dt≤L(0)+C2∫∞0exp(ςt)h(t)dt. |
Thanks to the hypothesis (H2), we can write
| L(T)≤C3exp(−C1T),C3>0, |
which yields the serial result (4.19), using the fact that F3(t),F4(t) are positive and the other side of the equivalence relation (4.16) again. The proof is complete.
In this section, we will solve numerically the system (1.9)–(1.10) in the one-dimension domain. For that, we use the classic finite difference method for the spatial and temporal discretization. Furthermore, in order to verify the asymptotic behavior of the solution of the discretized problem, we give an example in which the numerical experiment shows that the discrete energy En decays exponentially for different choices of the system parameters. Let us introduce the functions ˆφ=φt, and for any M,N∈N, we introduce the nets
| ΩN={xi=iΔx,i=0,...,N+1 where Δx=1N+1}, |
| ΓM={tn=nΔt,n=0,...,M+1 where Δt=TM+1}. |
Our problem is to find (ˆφ,ψ) satisfying the following numerical scheme:
| {ρ1Δt(ˆφni−ˆφn−1i)=k(Δx)2(φni+1−2φni+φni−1)+k2Δx(ψni+1−ψni−1)−μ1ˆφni−ρ1(Δt)2∫tn0h(tn−s)(ˆφn′i−ˆφn′−1i)ds+h(tn)φ1(xi), −ρ22ΔxΔt(ˆφni+1−ˆφni−1)=−ρ22ΔxΔt(ˆφn−1i+1−ˆφn−1i−1)+b(Δx)2(ψni+1−2ψni+ψni−1)−k2Δx(φni+1−φni−1)−kψni, | (5.1) |
where sn′=n′Δsn′, n′=0,...,M′+1 with Δsn′=tnM′+1, φni=φ(xi,tn), ˆφni=φt(xi,tn), ψni=ψ(xi,tn), ˆψni=ψt(xi,tn), for all i=1,...,N and n = 1, ..., M . To simplify our numerical calculations in our scheme, we consider the discrete boundary conditions given by
| \begin{equation} \left\{ \begin{array}{l} \psi _{0}^{n} = \psi _{N+1}^{n} = \varphi _{N+1}^{n} = \varphi _{0}^{n} = 0, \end{array} \right. \end{equation} | (5.2) |
and initial conditions
| \begin{equation} \psi _{i}^{0} = \psi _{0}\left( x_{i}\right) , \;\hat{\psi}_{i}^{0} = \psi _{1}\left( x_{i}\right) , \;\varphi _{i}^{0} = \varphi _{0}\left( x_{i}\right), \;\hat{\varphi}_{i}^{0} = \varphi _{1}\left( x_{i}\right), \end{equation} | (5.3) |
where
| \begin{equation*} \varphi _{i}^{n} = \varphi _{i}^{n-1}+\Delta t\hat{\varphi}_{i}^{n}, \; \psi _{i}^{n} = \psi _{i}^{n-1}+\Delta t\hat{\psi}_{i}^{n}, \end{equation*} |
for all i = 1, ..., N and n = 1, ..., M .
Note that to find \left(\hat{\varphi}, \psi \right) , we need to solve two coupled systems of algebraic equations. So, to solve the problem (5.1)–(5.3) at each time step, we propose to consider the following fixed-point algorithm that is stopped when the difference between two successive iterations becomes smaller than a given tolerance \varepsilon .
| \begin{equation} \left\{ \begin{array}{l} \hat{\varphi}_{i}^{n, l} = \dfrac{k}{c_{1}\left( \Delta x\right) ^{2}}\left( \varphi _{i+1}^{n, l-1}-2\varphi _{i}^{n, l-1}+\varphi _{i-1}^{n, l-1}\right) + \dfrac{k}{c_{1}2\Delta x}\left( \psi _{i+1}^{n, l-1}-\psi _{i-1}^{n, l-1}\right) \\ +\dfrac{\rho _{1}}{c_{1}\Delta t}\hat{\varphi}_{i}^{n-1}-\dfrac{\rho _{1}}{ \left( \Delta t\right) ^{2}}\int_{0}^{t_{n}}h\left( t_{n}-s\right) \left( \hat{\varphi}_{i}^{n^{\prime }, l-1}-\hat{\varphi}_{i}^{n^{\prime }-1, l-1}\right) ds+h\left( t_{n}\right) \varphi _{1}\left( x_{i}\right) \text{, } \\ \dfrac{b}{\left( \Delta x\right) ^{2}}\psi _{i+1}^{n, l}-\left( 2\dfrac{b}{ \left( \Delta x\right) ^{2}}+k\right) \psi _{i}^{n, l}+\dfrac{b}{\left( \Delta x\right) ^{2}}\psi _{i-1}^{n, l} = \dfrac{-\rho _{2}}{2\Delta x\Delta t} \left( \hat{\varphi}_{i+1}^{n, l}-\hat{\varphi}_{i-1}^{n, l}\right) \\ +\dfrac{\rho _{2}}{2\Delta x\Delta t}\left( \hat{\varphi}_{i+1}^{n-1, l}-\hat{ \varphi}_{i-1}^{n-1, l}\right) +\dfrac{k}{2\Delta x}\left( \varphi _{i+1}^{n, l}-\varphi _{i-1}^{n, l}\right) \text{, } \end{array} \right. \end{equation} | (5.4) |
with
| \begin{equation*} \left\{ \begin{array}{l} \varphi _{i}^{n, 0} = \varphi _{i}^{n-1}, \;\psi _{i}^{n, 0} = \psi _{i}^{n-1}, \;\varphi _{i}^{n, l} = \varphi _{i}^{n-1}+\Delta t\hat{\varphi }_{i}^{n, l}, \\ \psi _{i}^{n, l} = \psi _{i}^{n-1}+\Delta t\hat{\psi}_{i}^{n, l}, \end{array} \right. \end{equation*} |
for all i = 1, ..., N and n = 1, ..., M and l = 1, 2...
To approximate the continuous energy (3.1), we use the trapezoidal quadrature formula to compute the integral I = \int_{0}^{1}f(x)dx :
| \begin{equation*} I_{N} = \sum\limits_{i = 1}^{N}a_{i}f(x_{i})\approx I, \end{equation*} |
where the weights \left\{ a_{i}\right\} _{i = 1}^{N} are given by a_{1} = a_{N} = \dfrac{K}{2} , for i = 2, 3, ..., N-1, a_{i} = K with K = \dfrac{1 }{N}.
The same quadrature formula is used to evaluate the integral with respect to s at each time step t_{n}. Therefore, the discrete energy formula is given by
| \begin{align} E(t_{n})& \approx J^{n} = \frac{1}{2}\sum\limits_{i = 1}^{N}a_{i}[\rho _{1}\left( \hat{ \varphi}_{i}^{n}\right) ^{2}\ +k\left( \left( \varphi _{x}\right) _{i}^{n}+\psi _{i}^{n}\right) ^{2}+\frac{\rho _{2}\rho _{1}}{k}\left( \left( \hat{\varphi}_{t}\right) _{i}^{n}\right) ^{2} \\ & +\rho _{2}\left( \left( \varphi _{tx}\right) _{i}^{n}\right) ^{2}+b\left( \left( \psi _{x}\right) _{i}^{n}\right) ^{2}]+\rho _{1}(h_{n}\ast \hat{ \varphi}_{i}^{n}) \\ & +\frac{\rho _{2}\rho _{1}}{k}(h_{n}\ast \left( \hat{\varphi}_{t}\right) _{i}^{n}), \end{align} | (5.5) |
with
| \begin{gather*} \hat{\varphi}_{i}^{n} = \varphi _{t}\left( x_{i}, t_{n}\right) , \;\left( \hat{\varphi}_{t}\right) _{i}^{n} = \dfrac{1}{\Delta t}\left( \hat{\varphi} _{i}^{n+1}-\hat{\varphi}_{i}^{n}\right) , \\ \left( \hat{\varphi}_{t}\right) _{i}^{n} = \dfrac{1}{\Delta t}\left( \hat{ \varphi}_{i}^{n+1}-\hat{\varphi}_{i}^{n}\right) , \end{gather*} |
| \begin{equation*} \left( \varphi _{x}\right) _{i}^{n} = \frac{\varphi _{i+1}^{n}-\varphi _{i-1}^{n}}{2\Delta x}, \;\left( \psi _{x}\right) _{i}^{n} = \frac{\psi _{i+1}^{n}-\psi _{i-1}^{n}}{2\Delta x}\text{ and }\left( \varphi _{tx}\right) _{i}^{n} = \frac{\hat{\varphi}_{i+1}^{n}-\hat{\varphi}_{i-1}^{n}}{ 2\Delta x}. \end{equation*} |
Next, we describe the following numerical example:
Example 1. For this numerical test, we choose the following different values for the coefficients of the system:
| \begin{equation*} \rho _{1} = 1.1, \;\rho _{2} = 10, \;k = 0.01, \;\mu _{1} = 10, \text{ }b = 1.5. \end{equation*} |
We run our code for the following discretization parameters: N = 100, M = 200 , T = 1 . We take \varepsilon = 10^{-5} . Also, we choose the following initial conditions:
| \begin{eqnarray*} \varphi _{0}\left( x\right) & = &\frac{17}{20}x^{2}e^{-2x}, \;\varphi _{1}\left( x\right) = \frac{1}{4}\left( x^{3}-\frac{2}{3}x^{2}\right) , \text{ }h(t) = \exp (-4t), \\ \psi _{0}\left( x\right) & = &x^{3}\left( 1-x\right) ^{2}, \;\varphi _{2}\left( x\right) = x^{3}-\frac{2}{3}x^{2}. \end{eqnarray*} |
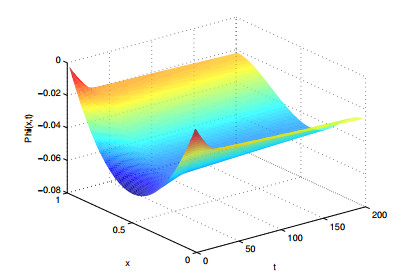
Here are the evolution in time of the solutions \varphi and \psi , the discrete energy and the evolution with respect to x of \varphi throughout time.
In the above numerical example, the graphics presented in Figures 1 and 2 show the evolution in time of the approximation solutions \varphi and \psi on the interval \left[0, T\right] , for different choices of the system parameters and of the initial data. Furthermore, Figures 3 and 4 show that the approximate energy (5.5) decays in an exponential manner, which confirms the main theoretical result obtained and the evolution of \varphi with respect to x throughout time.
In this work we investigated the sufficient conditions on the kernel of the neutral delay term to assure the exponential stability of solutions of the Bresse-Timoshenko system subject to this complementary control based on the multipliers technique to construct a suitable Lyapunov functional that allows us to estimate the energy of the considered system. As a future work, we propose to consider the same problem without dissipation due to the frictional damping, and we will search for additional conditions on the kernel of neutral delay term from which the energy can be decreased in an exponential manner.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
This research has been funded by the Deputy for Research Innovation, Ministry of Education through Initiative of Institutional Funding at University of Ha'il-Saudi Arabia through project number IFP-22142.
The authors declare that they have no competing interests.
| [1] | C. Abdallah, P. Dorato, J. Benitez-Read, R. Byrne, Delayed positive feedback can stabilize oscillatory system, 1993 American Control Conference, San Francisco, USA, 1993, 3106–3107. https://doi.org/10.23919/ACC.1993.4793475 |
| [2] |
B. Almarri, S. Janaki, V. Ganesan, A. H. Ali, K. Nonlaopon, O. Bazighifan, Novel oscillation theorems and symmetric properties of nonlinear delay differential equations of fourth-order with a middle term, Symmetry, 14 (2022), 585. https://doi.org/10.3390/sym14030585 doi: 10.3390/sym14030585

|
| [3] |
B. Almarri, A. H. Ali, A. M. Lopes, O. Bazighifan, Nonlinear differential equations with distributed delay: some new oscillatory solutions, Mathematics, 10 (2022), 995. https://doi.org/10.3390/math10060995 doi: 10.3390/math10060995

|
| [4] | T. A. Apalara, S. A. Messaoudi, M. I. Mustafa, Energy decay in thermoelastic type Ⅲ with viscoelastic damping and delay, Electron. J. Differ. Eq., 2012 (2012), 128. |
| [5] |
J. Awrejcewicz, A. V. Krysko, V. Soldatov, V. A. Krysko, Analysis of the nonlinear dynamics of the Timoshenko flexible beams using wavelets, J. Comput. Nonlinear Dynam., 7 (2012), 011005. https://doi.org/10.1115/1.4004376 doi: 10.1115/1.4004376

|
| [6] |
J. Awrejcewicz, A. V. Krysko, S. P. Pavlov, M. V. Zhigalov, V. A. Krysko, Stability of the size-dependent and fnctionally graded curvilinear Timoshenko beams, J. Comput. Nonlinear Dynam., 12 (2017), 041018. https://doi.org/10.1115/1.4035668 doi: 10.1115/1.4035668

|
| [7] |
J. Awrejcewicz, A. V. Krysko, S. P. Pavlov, M. V. Zhigalov, V. A. Krysko, Chaotic dynamics of size dependent Timoshenko beams with functionally graded properties along their thickness, Mech. Syst. Signal Pr., 93 (2017), 415–430. https://doi.org/10.1016/j.ymssp.2017.01.047 doi: 10.1016/j.ymssp.2017.01.047

|
| [8] |
J. Awrejcewicz, V. A. Krysko, S. P. Pavlov, M. V. Zhigalov, L. A. Kalutsky, A. V. Krysko, Thermoelastic vibrations of Timoshenko microbeam based on the modified couple stress theory, Nonlinear Dyn., 99 (2020), 919–943. https://doi.org/10.1007/s11071-019-04976-w doi: 10.1007/s11071-019-04976-w

|
| [9] | J. Awrejcewicz, V. A. Krysko, I. V. Papkova, A. V. Krysko, Deterministic chaos in one-dimensional continuous systems, Singapore: World Scientific, 2016. https://doi.org/10.1142/9775 |
| [10] |
R. Datko, Not all feedback stabilized hyperbolic systems are robust with respect to small time delays in their feedbacks, SIAM J. Control Optim., 26 (1988), 697–713. https://doi.org/10.1137/0326040 doi: 10.1137/0326040

|
| [11] |
R. Datko, J. Lagnese, M. P. Polis, An example on the effect of time delays in boundary feedback stabilization of wave equations, SIAM J. Control Optim., 24 (1986), 152–156. https://doi.org/10.1137/0324007 doi: 10.1137/0324007

|
| [12] |
R. D. Driver, A mixed neutral system, Nonlinear Anal. Theor., 8 (1984), 155–158. https://doi.org/10.1016/0362-546X(84)90066-X doi: 10.1016/0362-546X(84)90066-X

|
| [13] | I. Elishakoff, An equation both more consistent and simpler than the Bresse-Timoshenko equation, In: Advanced in mathematical modeling and experimental methods for materials and structures, Dordrecht: Springer, 2009, 249–254. https://doi.org/10.1007/978-90-481-3467-0_19 |
| [14] |
I. Elishakoff, J. Kaplunov, E. Nolde, Celebrating the centenary of Timoshenko's study of effects of shear deformation and rotary inertia, Appl. Mech. Rev., 67 (2015), 060802. https://doi.org/10.1115/1.4031965 doi: 10.1115/1.4031965

|
| [15] |
I. Elishakoff, F. Hache, N. Challamel, Critical contrasting of three versions of vibrating Bresse-Timoshenko beam with a crack, Int. J. Solids Struct., 109 (2017), 143–151. https://doi.org/10.1016/j.ijsolstr.2017.01.015 doi: 10.1016/j.ijsolstr.2017.01.015

|
| [16] |
E. H. Morales, H. R. Henriquez, M. A. McKibben, Existence of solutions for second order partial neutral functional differential equations, Integr. Equ. Oper. Theory, 62 (2008), 191–217. https://doi.org/10.1007/s00020-008-1618-1 doi: 10.1007/s00020-008-1618-1

|
| [17] |
A. Guesmia, Well-posedness and exponential stability of an abstract evolution equation with infinity memory and time delay, IMA J. Math. Control I., 30 (2013), 507–526. https://doi.org/10.1093/imamci/dns039 doi: 10.1093/imamci/dns039

|
| [18] |
D. S. A. Junior, I. Elishakoff, A. J. A. Ramos, L. G. R. Miranda, The hypothesis of equal wave speeds for stabilization of Timoshenko beam is not necessary anymore: the time delay cases, IMA J. Appl. Math., 84 (2019), 763–796. https://doi.org/ 10.1093/imamat/hxz014 doi: 10.1093/imamat/hxz014

|
| [19] |
D. S. A. Junior, A. J. A. Ramos, On the nature of dissipative Timoshenko systems at light of the second spectrum, Z. Angew. Math. Phys., 68 (2017), 145. https://doi.org/10.1007/s00033-017-0881-x doi: 10.1007/s00033-017-0881-x

|
| [20] | H. E. Khochemane, S. Zitouni, L. Bouzettouta, Stability result for a nonlinear damping porous-elastic system with delay term, Nonlinear Studies, 27 (2020), 487–503. |
| [21] |
H. E. Khochemane, L. Bouzettouta, A. Guerouah, Exponential decay and well-posedness for a one-dimensional porous-elastic system with distributed delay, Appl. Anal., 100 (2021), 2950–2964. https://doi.org/10.1080/00036811.2019.1703958 doi: 10.1080/00036811.2019.1703958

|
| [22] | C. Lanczos, The variational principles of mechanics, New York: Dover Publications, 1964. |
| [23] |
G. Liu, J. Yan, Global asymptotic stability of nonlinear neutral differential equation, Commun. Nonlinear Sci., 19 (2014), 1035–1041. https://doi.org/10.1016/j.cnsns.2013.08.035 doi: 10.1016/j.cnsns.2013.08.035

|
| [24] |
S. Loucif, R. Guefaifia, S. Zitouni, H. E. Khochemane, Global well-posedness and exponential decay of fully dynamic and electrostatic or quasi-static piezoelectric beams subject to a neutral delay, Z. Angew. Math. Phys., 74 (2023), 83. https://doi.org/10.1007/s00033-023-01972-4 doi: 10.1007/s00033-023-01972-4

|
| [25] |
S. Nicaise, C. Pignotti, Stabilization of the wave equation with boundary or internal distributed delay, Differ. Integral Equ., 21 (2008), 935–958. https://doi.org/10.57262/die/1356038593 doi: 10.57262/die/1356038593

|
| [26] |
S. Nicaise, C. Pignotti, Stability and instability results of the wave equation with a delay term in the boundary or internal feedbacks, SIAM J. Control Optim., 45 (2006), 1561–1585. https://doi.org/10.1137/060648891 doi: 10.1137/060648891

|
| [27] |
R. Racke, Instability of coupled systems with delay, Commun. Pur. Appl. Anal., 11 (2012), 1753–1773. https://doi.org/10.3934/cpaa.2012.11.1753 doi: 10.3934/cpaa.2012.11.1753

|
| [28] | J. W. S. Rayleigh, The theory of sound, Cambridge: Cambridge University Press, 1877. https://doi.org/10.1017/CBO9781139058087 |
| [29] |
L. Seghour, N. E. Tatar, A. Berkani, Stability of a thermoelastic laminated system subject to a neutral delay, Math. Method. Appl. Sci., 43 (2020), 281–304. https://doi.org/10.1002/mma.5878 doi: 10.1002/mma.5878

|
| [30] |
N. E. Tatar, Stability for the damped wave equation with neutral delay, Math. Nach., 290 (2017), 2401–2412. https://doi.org/10.1002/mana.201600229 doi: 10.1002/mana.201600229

|
| [31] |
S. P. Timoshenko, On the correction for shear of the differential equation for transverse vibrations of prismatic bars, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 6 (1921), 744–746. https://doi.org/10.1080/14786442108636264 doi: 10.1080/14786442108636264

|
| [32] | J. Wang, Existence and stability of solutions for neutral differential equations with delay, International Conference on Multimedia Technology (ICMT), Hangzhou, China, 2011, 2462–2465. https://doi.org/10.1109/ICMT.2011.6002527 |
| [33] |
G. Q. Xu, S. P. Yung, L. K. Li, Stabilization of wave systems with input delay in the boundary control, ESAIM Control Optim. Calc. Var., 12 (2006), 770–785. https://doi.org/10.1051/cocv:2006021 doi: 10.1051/cocv:2006021

|
| [34] |
K. Zennir, D. Ouchenane, A. Choucha, M. Biomy, Well-posedness and stability for Bresse-Timoshenko type systems with thermodiffusion effects and nonlinear damping, AIMS Mathematics, 6 (2021), 2704–2721. https://doi.org/10.3934/math.2021164 doi: 10.3934/math.2021164

|
| 1. | Sami Loucif, Rafik Guefaifia, Houssem Eddine Khochemane, Salah Zitouni, Well-posedness and exponential stability of piezoelectric beam with thermal effect and boundary or internal distributed delay, 2024, 0149-5739, 1, 10.1080/01495739.2024.2418538 |