1.
Introduction
As usual, let τ(m) be the divisor function. The famous Dirichlet divisor problem on τ(m) has attracted many authors. For example, the best result to date was established by Bourgain and Watt [2], who obtained that
with Euler's constant γ.
Let 1≤k<l be fixed integers. Denote by τ(m;k,l) the number of representations of m as m=mk1ml2, where m1,m2 are natural numbers, that is,
In 1969, Krätzel [13] proved that
where
ζ is the Riemann zeta function, ψ(z)=z−[z]−12 and [z] denotes the integer part of z. After that, a lot of results have been established in this direction. We refer to Ivić [8, Chapter 14] for details.
Now we draw attention to the Hecke eigenvalues. Denote by SL2(Z) the full modular group and by Hκ the set of primitive holomorphic cusp forms g(z) of weight κ for SL2(Z), respectively, where κ≥2 is an even integer. It is known that Hκ is composed of the eigenfunctions of all Hecke operators. And at the cusp ∞, g(z) has the Fourier expansion:
where λg(m) is the m-th normalized Hecke eigenvalue. For prime number p, one has
Then define the Hecke L-function L(g,s) attached to g as
Further, define the Rankin-Selberg L-function as
Therefore, we have
Many scholars have studied λg(m) and λg×g(m) in various ways and established a lot of results (for example, see [3,4,6,9,11,12,14,15,16,17,18,19,20,21,22,23,24,25], etc.). In addition, one may prefer to consider
Recently, Huang, Liu and Xu [7] studied the general two-dimensional divisor problems involving Hecke eigenvalues and proved that for any ε>0,
where C1=L(sym2g,1)L(g×g,lk) and C2=L(sym2g,1)L(g×g,l2). In this paper, we are able to improve the above result by proving the following theorem.
Theorem 1.1. Let 1≤k<l be any fixed integers. Then for any ε>0, we have
where
To prove Theorem 1.1, we mainly use the Perron's formula and the individual and averaged subconvexity bounds for the Riemann zeta-function and the symmetric square L-function.
2.
Preliminary lemmas
Firstly, we introduce the symmetric square L-function L(sym2g,s) defined by
Write s=σ+it. Let ε be a sufficiently small positive constant, whose value is not necessarily the same at each occurrence.
Lemma 2.1. We have
Proof. We can find this lemma in [7].
Lemma 2.2. We have, uniformly for T≥1,
and for 12<σ≤1,|t|≥1,
Proof. We can obtain the former result (2.2) from the properties of L(sym2g,s) with standard arguments. The latter result (2.3) was proved by Nunes [18].
Lemma 2.3. We have, uniformly for T≥1 and 12≤σ<1,
and for 12<σ≤1,|t|≥1,
Proof. The result (2.4) with σ=12 is the classical result of Ingham. We can find the result (2.4) in [8]. The third result (2.5) was derived by Bourgain [1].
3.
Proof of Theorem 1.1
Note that
Then from (3.1) and Perron's formula (see [10, Proposition 5.54]), with a similar argument to [8, page 411] we get
where ξ=1k+ε and T is a parameter to be determined later. Then we shift the integral line of (3.2) to the parallel line Re s=12k. From Gelbart-Jacquet [5], we note that L(sym2g,s) is holomorphic at s=1. Considering the sizes of l and 2k, we see that s=1k and s=1l will be the only possible simple poles in RT:={s=σ+it:12k≤σ≤ξ,∣t∣≤T} according to (2.1), and the corresponding residues at s=1k and s=1l are
respectively.
In the following argument, we still carry out the discussion by two cases 2k≥l and 2k<l. In the case 2k≥l, both s=1k and s=1l are simple poles in RT. Then we derive from Cauchy's residue theorem,
To estimate J2 and J3, we also need to divide the integral interval into two arcs A′1,A′2 and draw support from Lemmas 2.2 and 2.3.
A′1:={s=σ+iT:12k≤σ≤1l}. Then in this arc we have
A′2:={s=σ+iT:1l<σ≤1k}. Then in this arc we can get
From (3.4) and (3.5) we get
While for J1, we have
Then by Hölder's inequality, Lemmas 2.2 and 2.3, one can get
Therefore, from (3.3), (3.6) and (3.7), we can establish
Taking T=y420k−5l in (3.8), we have
Thus, we prove the first part of Theorem 1.1.
For 2k<l, s=1k is the only simple pole in the range RT by nothing 1l<12k. Then from Cauchy's residue theorem, we can derive
To estimate J′2 and J′3, we also split the integral interval into two arcs A′1∗,A′2∗ but with different ranges from the case 2k≥l. By a similar argument, we can get
Note that l2k>1. The estimate of J′1 becomes
Therefore, recalling (3.9) we can get
Taking T=y25k in (3.10), we have
Thus, the prove of Theorem 1.1 is finished.
4.
Conclusions
In this paper, we investigate the average behaviors of the Fourier coefficients λk,lg×g(m) and improve the previous estimates in this direction. Here, the condition 1≤k<l in Theorem 1.1 removes the complexity of discussing the sizes between k and l due to the symmetry. To give a sharper upper bounds for the sum ∑m≤yλk,lg×g(m), we apply some analytic instruments such as Perron's formula, the decomposition of the Rankin-Selberg L-function, and the individual and averaged subconvexity bounds for the Riemann zeta-function and the symmetric square L-function. With the help of results in Theorem 1.1, we can understand the Fourier coefficients λk,lg×g(m) on average more precisely.
Acknowledgments
This work was supported by National Natural Science Foundations of China (Grant Nos. 11801328, 11771256 and 11801318) and Young Scholars Program of Shandong University, Weihai (Grant No. 20820211012).
Conflict of interest
The authors declare no conflicts of interest.









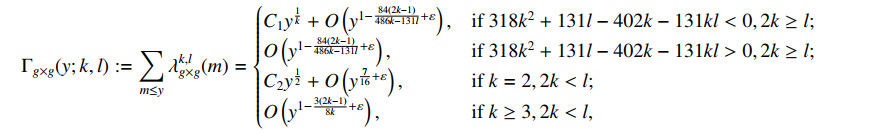




 DownLoad:
DownLoad: